丽江市古城区地质灾害易发性评价方法对比

葛宗旭，刘汉湖，陈 行

(成都理工大学 地球科学学院，四川 成都 610051)

0 引言

中国国土广袤，地质条件复杂，地貌类型多样。根据自然资源部发布的2021年中国地质灾害信息，全国共发生地质灾害4 772起，造成80人死亡、11人失踪，直接经济损失32亿元。其中滑坡是最常见的地质灾害，云南省每年因大量滑坡造成的财产损失多达上亿元。因此为了降低地质灾害所带来的危害，保证人民群众的生命和财产安全开展滑坡易发性评价具有十分重要的社会意义。

滑坡易发性模型主要有信息量[1]、层次分析[2]、确定性系数[3]、逻辑回归[4]、人工神经网络[5]、随机森林[6]以及多种方法耦合模型。在运用信息量的模型中，余杰[7]等运用信息量模型对黄梅县的地质灾害进行了易发性评价；朱永浩[8]等也运用信息量模型对翁安县的滑坡崩塌进行了易发性的分区评价。此外对于确定性系数模型，屠水云[9]等利用CF-LR模型分析了地质灾害的易发性。

综上本文选择了统计预测模型中应用较简单，操作更容易实现的信息量和确定性系数两种模型对丽江市古城区分别进行滑坡的易发性评价，采用ROC曲线对两种模型进行精度评价，以求得到更加准确的结果来反映该地区的滑坡易发性，并制作其易发性区域图，为当地的灾害防治工作提供参考。

1 研究区概况及数据源

1.1 研究区概况

丽江市古城区的地理位置如图1所示。古城区位于云南省西北部的丽江市中部，隶属于丽江市。古城区东隔金沙江与丽江市宁蒗县和永胜县相望，南与大理州鹤庆县接壤，西与丽江市玉龙县相连，地理坐标东经99°23′～100°32′，北纬26°34′～27°46′，面积1 255.40 km2。古城区距省会昆明市502 km，是丽江市政治、经济、文化中心。境内主要交通干线有丽江—永胜(S308)、丽江—鸣音、丽江—宁蒗(S221)、丽江—鹤庆(S221)公路及丽江—机场高速公路，境内区乡公路交通网络发达，交通较为便利。古城区位于青藏高原南延横断山纵谷地带，地势北高南低，地形起伏大，山川走向均以南北向为主，河谷深切，山高坡陡、侵蚀作用强烈。金沙江沿古城区地域东侧由北向南流过，区内属金沙江水系，羽状支流发育，水力坡度较大。区内地质构造活动强烈，褶皱、断裂发育，地层岩性较为复杂。

图1 研究区位置示意图(审图号：GS(2020)4619号，下同)

1.2 数据来源

本文使用的数据包括：分辨率30 m的ASTER GDEM数字高程模型和道路数据来源于地理空间数据云(https：//www.gscloud.cn/)；水文数据来源于中国地质调查局地质云2.0(https：//geocloud.cgs.gov.cn/)；气象数据来源于中国气象数据共享服务网(cdc.nimc.cn/home.do)；Landsat系列卫星数据(http：//earthexplorer.usgs. gov/)，并利用Landsat8影像提取的NDVI；断层数据来源于古城区地质图矢量数据；野外地质灾害调查资料收集的164处滑坡点数据。

2 研究方法

2.1 信息量模型

信息量模型通过计算分析获得各影响因子不同区间的信息量，来定量表示环境因子各属性区间对滑坡灾害的影响程度，再通过叠加各因子得到综合水平信息量[10]，进而对部分区域进行易发性划分。计算得出的信息量值越大，说明该因子对于地质灾害发生的贡献值越大。信息量模型可以客观地、准确地评价各因子对地质灾害发生的贡献值，但选取的因子不同导致结果不同，可比性较差。

其计算公式为：

(1)

式中：IAi为A因子下i区间地质灾害发生的信息量值；Ni为A因子下i区间地质灾害分布的单元数(或面积)；N为研究区已有地质灾害分布的单元总数(或面积)；Si为表示A因子下i区间地质灾害分布的单元数(或面积)；S为研究区的单元总数(或面积)。

选择区内对地质灾害发生有决策作用的因子，利用信息量模型，计算出不同因子不同区间的信息量值，对因子进行信息量叠加，得到研究区的地质灾害易发性的指数，并对栅格进行归一化，按自然分类断点法划分等级。

2.2 确定性系数模型

确定性系数(Certainty Factor，CF)本质上是一个概率函数，主要用来计算影响地质灾害发生的各个评价因子的敏感性[11]。由Shortliffe E H和Buchanan B G提出[12]，并由Heckerman D改进[13]。计算得到的CF值可以表示不同因子不同级别下地质灾害发生的可能性。

其计算公式为：

(2)

式中：PPa为影响因子a贡献的地质灾害发生的概率，通常用研究区内分布在a因子的地质灾害数量与影响因子a的面积之比来表示；PPs为地质灾害在研究区内发生的先验概率，通常用研究区内地质灾害的总数与整个研究区的面积之比来表示。

CF值为确定性系数，取值区间为[-1，1]，正值表示地质灾害发生的确定性大，越接近1越易于发生地质灾害；负值表示地质灾害发生确定性小，越接近1越不易于发生地质灾害；值为0时表示条件概率和先验概率相同，不确定是否会发生地质灾害[14]。

2.3 ROC曲线

受试者工作特征(Receiver Operating Characteristic，ROC)曲线，因其简单、直观的特点，又称为感受性曲线。该模型横坐标假阳性率(False Positive Rate)代表非滑坡预测为滑坡，纵坐标真阳性率(True Positive Rate)代表滑坡预测为滑坡。ROC曲线法是通过ROC曲线下面积(Area Under Curve，AUC)来反映和比较模型的评价预测精度[11]。AUC越大，说明该模型的精度越高。

3 评价因子的选取与易发性评价结果的对比

3.1 评价因子的选取

根据古城区滑坡等地质灾害发育规律，在结合古城区地质条件，前人经验，野外验证等基础上，选择高程、坡度、坡向、距道路距离、距水系距离、降雨量、距断层距离、NDVI等8类影响因子作为此次评价的指标(图2)。

图2 评价因子分级

3.1.1 高程

滑坡的发生概率与高程密切相关，不同的高程对滑坡的贡献度也不同。古城区的高程主要集中在1 172～3 647 m。研究区内以自然间断法与等间距分类并用把高程分为5个级别：[1 172 m，1 800 m)、[1 800 m，2 200 m)、[2 200 m，2 600 m)、[2 600 m，3 000 m)、[3 000 m，3 647 m]。

3.1.2 坡度

古城区的坡度可由分辨率为30 m的ASTER GDEM得到。

坡度一定程度上表示地面倾斜程度，对滑坡的发生具有一定影响，将坡度按等间距分可把坡度分为[0°，15°)、[15°，30°)、[30°，45°)、[45°，60°)、[60°，73°]。

3.1.3 坡向

不同坡向的光照强度影响着植被覆盖、斜坡体稳定性[15]。将研究区坡向分为8个方向：北(N)、东北(NE)、东(E)、东南(SE)、南(S)、西南(SW)、西(W)、西北(NW)。其中S、SE和NE坡向占到滑坡总数的59%。

3.1.4 距道路距离

根据已有资料，在一定的距离内，距道路距离越近，滑坡的数量越多说明发生滑坡的概率越高。所以将滑坡距道路小于3 000 m按间距分为[0，500 m)、[500 m，1 000 m)、[1 000 m，2 000 m)、[2 000 m，3 000 m)这4个区间。

3.1.5 距水系距离

古城区东侧为金沙江流域，距离河流越近，其对地质灾害的影响越大。利用ArcGIS平台的欧氏距离工具，把距离水系等间距划分为5个级别：[0，500 m)、[500 m，1 000 m)、[1 000 m，1 500 m)、[1 500 m，2 000 m)、≥2 000 m。

3.1.6 降雨量

降水是滑坡发生的重要诱发因素，其增加了土壤含水量，减弱了地面的抗滑能力[16]。古城区的年降雨量为766～866 mm。将降雨量按自然间断点分级法和实际情况并用的方法分成5段。

3.1.7 距断层距离

断裂构造会破坏一定距离内的岩土构造，即也会促进滑坡的发生。研究区根据实际情况将分为[0，300 m)、[300 m，500 m)、[500 m，1 000 m)、[1 000 m，2 000 m)、≥2 000 m的5种区间。其中0～300 m占区内滑坡总个数40%。

3.1.8 NDVI

NDVI是最常用的植被指数。该因子的值域为[-1，1]，负值表示对可见光高反射，地面为江、河、湖泊等水体或有雪覆盖；0表示NIR和R波段的反射率近似相等，为岩石或裸地等；正值表示有植被覆盖，数值越大表示植被覆盖率越高[17]。对研究区NDVI进行归一化计算，研究区NDVI在0～1之间按植被实际分布情况分为6个级别：0～0.5为一个级别，后5个级别每隔0.1为一个级别。

3.2 易发性评价结果

利用ArcGIS平台，分别计算2种评价模型下各影响因子的不同区间内信息量值和CF值。对8种因子进行叠加分析，可以得到两种模型下古城区的滑坡易发性评价结果图。其中，信息量模型下信息量值的范围为[-7，4]。信息量越大，代表该区域越有可能发生滑坡等地质灾害。确定性系数模型下，对输出栅格进行归一化处理，CF值越高，该区域发生滑坡的概率越大。对最终得到的信息量值和确定性系数进行重分类，划分出低、较低、中等、较高、高5个滑坡易发性区域(表1)。

表1 各因子信息量与CF值

对于高程，滑坡在1 800 m以下的较低高程易发性较大，其信息量和CF值最大。滑坡在30°～45°和45°～60°分区上最多，占据滑坡总个数60%，说明在一定范围内，坡度越大越有利于滑坡的发生，其信息量和CF值越高。坡向方面，偏西方向因子信息量和CF值皆为负值，符合地理条件；在NDVI方面，在一定范围内，植被覆盖越高的地方，越不容易发生滑坡，其信息量值和CF值呈负相关。降雨方面，降雨因子在810～866 mm的分区对滑坡的贡献值最大。在距道路、断层等因子中，随着距离越近，分区的信息量值和CF值愈大。距离河流越远，灾害发生的次数呈现出逐渐减小的状态[18]。图3所示分别为运用信息量模型图(a)和确定性系数(b)对古城区进行易发性评价的结果。

(a)信息量模型易发性分级图

(b)确定性系数模型易发性分级图

4.3 易发性结果精度评价

如表2、3所示，在易发性评价较高，高的分区面积上，两种模型没有较大差异。信息量模型在较高、高易发区的面积为340.28 km2，占总面积的27.11%；而确定性系数模型在较高、高易发区的面积为249.51 km2，占总面积的19.88%。

表2 信息量模型易发性评价结果

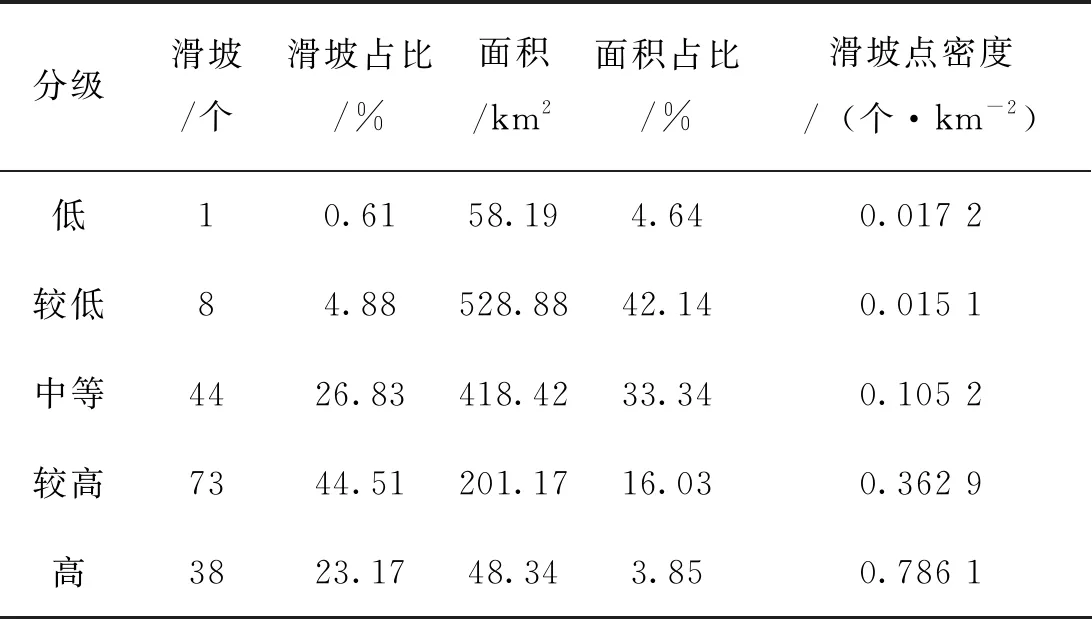
表3 确定性系数模型易发性评价结果

随机选择49处滑坡点(占30%)作为精度评价样本，并在已有滑坡点周围1 km建立缓冲区，再通过ArcGIS平台产生随机点选择同等的非灾害点。两者分别为0-敏感度，1-特异性作为横纵坐标，由SPSS软件得到ROC曲线来比较2种模型的精度(图4)。

图4 滑坡易发性评价精度预测曲线

ROC曲线下的面积AUC可以反映两种模型的精度结果，两种模型的AUC值分别为0.862，0.868、可以得出两种模型对该地区滑坡易发性评价的效果皆较好，结果较为精准。分析结果表明，确定性系数模型较优于信息量模型对该地区滑坡易发性的精度评价。

4 结论与讨论

4.1 结论

(1)本文以丽江市古城区为例，选择高程、坡度、坡向、距道路距离、距水系距离、降雨量、距断层距离、NDVI等因子，利用GIS和信息量、确定性系数模型对该地区的滑坡进行易发性评价，并绘制古城区滑坡易发性分级图。

(2)通过分析ROC曲线得出信息量模型的精度(AUC=0.862)，确定性系数模型的精度(AUC=0.868)，但CF模型的精度更好，更加符合该区域滑坡分布的实际情况。利用ROC曲线对评价模型进行精度评价，使得滑坡易发性结果更客观，更准确。

4.2 讨论

研究结果可为该地区灾害防治，未来城区规划、国土管理提供参考。建议在高、较高风险区域加强群测群防，开展工程治理。

本文仅用信息量模型和确定性系数模型进行易发性评价，不具备唯一性，对该地区的地质灾害易发性评价需进一步精进研究。