井下安全阀特殊气密封螺纹密封性能分析*

王传鸿 鄢标 周歆 邹刚 杨小城 孙巧雷

(1. 中石化石油机械股份有限公司 2.长江大学机械工程学院)

0 引 言

井下安全阀是一种连接在油管上的安全控保装置，当井口装置在发生火灾或爆炸等重大险情时，能迅速触发并关闭生产通道，防止事故进一步扩大。随着我国对清洁能源需求的日益增长和对安全环保生产的不断重视，井下安全阀作为必须使用的安全装置，被广泛应用于高含硫气田和海上油气田的开发中[1-2]。目前井下安全阀的核心技术仍然掌握在全球4大油服公司手上，虽然国内许多机构和企业也进行了大量的研究攻关，但仍然处于起步阶段[3]。

井下安全阀采用非弹性密封设计，壳体螺纹连接处的密封是井下安全阀研发的重要环节之一。关于螺纹连接处的密封结构，国内外学者进行了大量研究，常见的密封结构包括锥面对锥面密封、球面对锥面和球面对柱面密封3种结构。M.Y.GELFGAT和V.S.BASOVICH等[4-5]通过数值模拟和试验，研究了铝合金接头偏梯形螺纹和锥面密封结构的密封性能。许红林等[6]基于Hertz接触应力和Mises屈服准则，开展了油套管特殊螺纹球面对锥面密封结构的弹塑性接触应力分析。刘永刚等[7]以双台肩超高抗扭钻具连接螺纹为研究对象，研究了钻具螺纹应力与密封性能的影响因素。狄勤丰等[8]基于有限元法分析了磨损套管螺纹接头密封面的力学特性。韩鑫[9]研究了动载荷作用下特殊螺纹接头密封性能及密封判断依据。

虽然国内外对螺纹密封接头的设计研究较多，但均具有一定的针对性，多偏向于油管、套管或者钻杆[10-16]，关于适用于井下安全阀壳体连接的金属密封结构的研究相对较少。鉴于此，为充分实现大内径、小外径的设计原则，本文设计了一种锥面对球面密封的螺纹密封结构，以有效解决井下安全阀接头连接处螺纹密封问题。

1 密封结构设计及材料选择

井下安全阀螺纹密封部位主要涉及上接头、中间接头和下接头，螺纹密封结构如图1所示。螺纹连接分为外螺纹端和内螺纹端，内螺纹端密封面采用锥面设计，外螺纹端密封面采用球面设计，密封球面内侧设有一弹性凹槽，使密封球面发生一定的弯曲变形，以储存一定的弹性势能，弥补外载荷作用下造成的接触应力衰减。定位台肩位于外螺纹端，以抵抗扭矩载荷和形成二次密封。本文以ø88.9 mm油管连接用井下安全阀为研究对象，设计工作压力70 MPa。图1中θ为密封锥面倾角，L为密封球面弹性体厚度，R为密封球面半径。

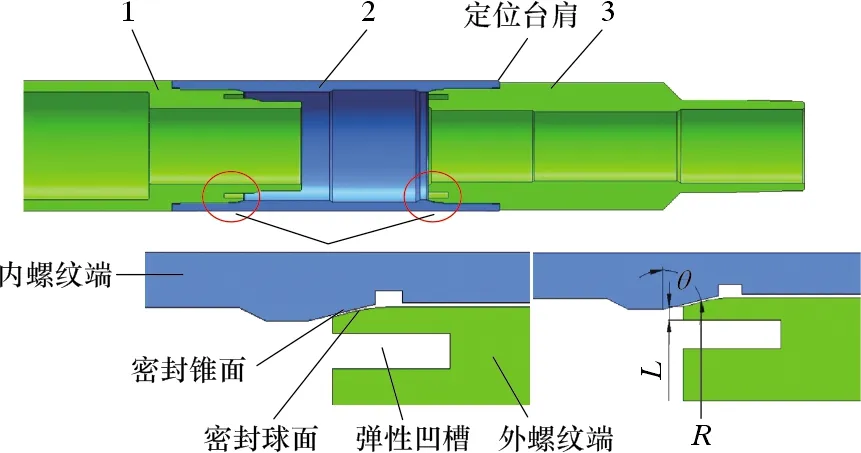
1—上接头；2—中间接头；3—下接头。图1 井下安全阀螺纹密封结构示意图Fig.1 Structure of thread seal of downhole safety valve

L80-13Cr具有较好的耐二氧化碳和海水腐蚀等性能，被广泛应用于井下工具的设计制造中。本次研究的井下安全阀螺纹密封结构仍选用L80-13Cr材料，其弹性模量为206 GMPa，泊松比为0.28，屈服强度为610 MPa，拉伸强度为816 MPa，断裂伸长率为22%，密度为7 850 kg/m3。

2 Hertz弹性接触应力

为明确设计变量，基于Hertz接触理论，建立了井下安全阀接头连接处锥面对球面密封结构，其弹性接触状态下的法向接触应力表达式为[17]：

(1)

式中：psN为密封面法向接触应力，MPa；E*为密封面当量弹性模量，MPa；R为密封球面半径，mm；ws为密封面有效接触半宽，mm；x的取值范围-ws≤x≤ws；ws的取值范围0≤2ws≤R。

对于轴对称或平面应变问题，E*可通过下式进行计算。

(2)

式中：Ep为密封球面材料的弹性模量，MPa；Ec为密封锥面材料的弹性模量，MPa；μp为密封球面材料的泊松比，无量纲；μc为密封锥面材料的泊松比，无量纲。

从式(2)可以看出，密封面的接触应力与密封球面半径、接触面宽度以及密封面的弹性模量和泊松比有关。本文设计的井下安全阀采用L80-13Cr材料，故弹性模量和泊松比对密封性能的影响将不在本文进行研究。本文主要研究过盈量、密封锥面倾角θ、密封球面弹性体厚度L和密封球面半径R对密封性能的影响。

3 有限元模型及仿真结果分析

3.1 密封结构有限元计算模型

井下安全阀螺纹密封结构形状相对复杂，涉及到几何非线性、材料非线性和接触非线性的强非线性问题，故本文采用有限元分析方法开展螺纹密封研究相关工作，因研究重点在于密封面结构参数的设计及优化，故此处可忽略螺纹啮合的影响。对于几何非线性，采用更新的拉格朗日方法处理结构的几何大变形；对于材料非线性问题，采用von Mises屈服准则、von Mises流动准则和各向同性硬化法则来描述材料的弹塑性力学行为。对于接触非线性，采用罚函数法引入接触面约束条件，构造修正泛函导出无约束条件的广义变分原理，并用硬接触模型和库伦摩擦模型分别描述接触面的法向和切向行为。

井下安全阀螺纹密封结构非线性力学分析中，因无需考虑惯性和阻尼对计算的影响，故采用静力学有限元分析方法进行即可，基本方程如下[18]。

平衡方程(在域V内)：

σij，j+PVi=0

(3)

几何方程(在域V内)：

(4)

本构方程(在域V内)：

σij=Dijklεkl

(5)

边界条件：

(6)

σijnj=PSi(在Sσ边界上)

(7)

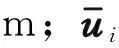
3.2 密封结构几何模型和网格划分

由于井下安全阀螺纹密封结构是轴对称模型，综合考虑计算精度和效率，计算模型可简化为轴对称模型，建模时接触部位留有初始间隙，以模拟整个装配过程。网格划分采用四边形网格形式，单元类型选取4节点双线性轴对称减缩积分单元CAX4R[19]。本文重点研究部位为锥面和球面密封的接触部位，故对该接触部位进行网格细化，以保证计算精度。几何模型和网格划分如图2所示。

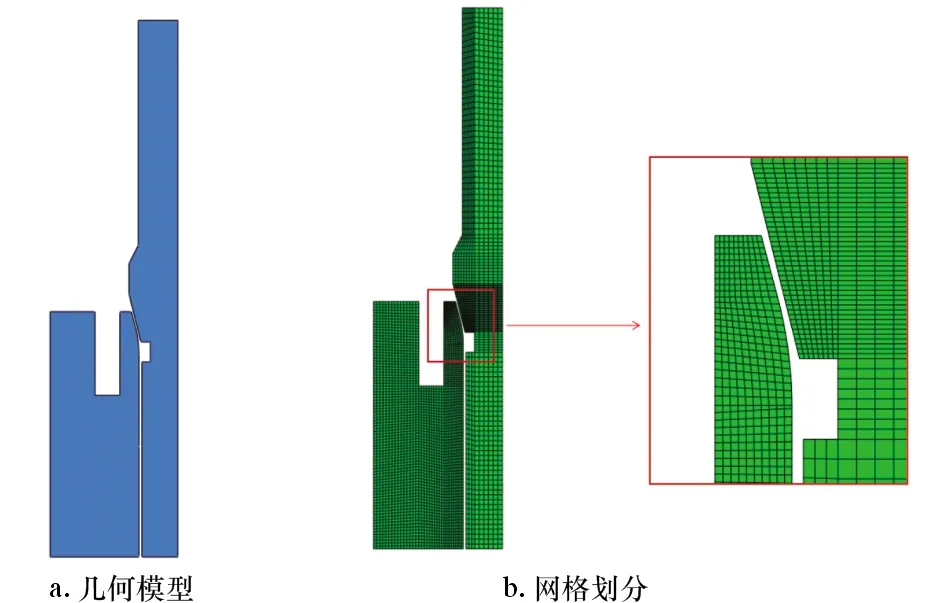
图2 几何模型和网格划分Fig.2 Geometric model and mesh division

3.3 载荷工况及关键路径

将密封锥面和密封球面间的密封区域定义为面面接触，采用主从接触算法计算轴向载荷作用下密封锥面和密封球面之间的相互作用。采用节点耦合技术，在外螺纹端建立distributing形式的节点耦合，以施加轴向位移载荷，用于模拟螺纹上紧过程，在内螺纹端建立kinematic形式的节点耦合，以施加固定约束。为了分析密封面上的接触应力分布情况，设置了如图3所示的沿密封面轴向的路径，路径起点为点A，终点为点B。

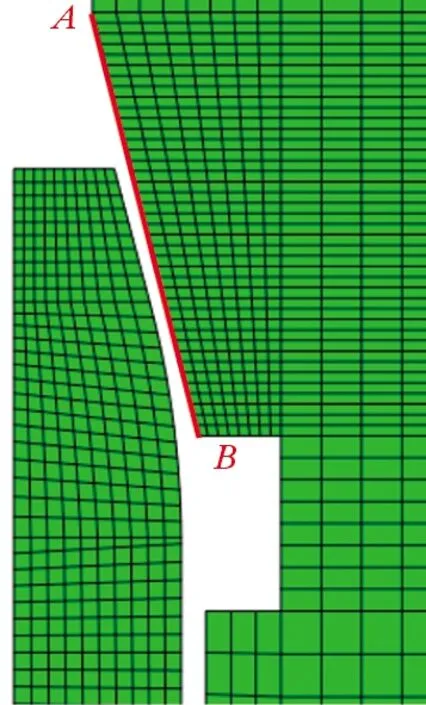
图3 关键路径定义Fig.3 Definition of critical path

4 结构参数对密封性能的影响

4.1 密封性能判断方法

目前关于金属密封性能的研究，主要考虑接触面的接触应力和结构整体的等效应力，当密封面接触应力大于垫片系数和介质压力的乘积时，可实现有效密封。秦桦等[20]开展了关于设计压力69 MPa的水下采油树油管悬挂器K 形金属密封环的相关试验研究，研究结果表明：当密封介质压力小于40 MPa时，金属密封环的最大接触压力大于介质压力的3倍，可实现可靠密封；当密封介质压力大于40 MPa时，最大接触压力超过介质压力的10 倍，可实现可靠密封。依据上述研究成果，结合本文研究工况，选取接触压力大于介质压力10倍作为密封设计准则。同时，为保证密封面性能和接头的整体强度，接头各部位的等效应力应不超过材料的屈服强度。本文选取接头各部位的最大等效应力刚好达到材料的屈服强度为极限工况点进行分析。

4.2 结构参数对密封性能的影响

采用控制变量法研究过盈量、锥面倾角θ、密封球面弹性体厚度L和密封球面半径R对密封性能的影响。其中：过盈量通过轴向位移载荷进行控制，其值等于施加的轴向位移与密封面初始接触时的轴向位移的差值。

4.2.1 锥面倾角对密封性能的影响

当密封球面弹性体厚度L=2.4 mm，密封球面半径R=25.4 mm，密封锥面倾角θ分别为73°、75°、76°和77°时，最大接触应力和最大等效应力与轴向位移的关系曲线分别如图4和图5所示。当轴向位移为4 mm时，接触应力沿路径A→B的分布规律如图6所示。

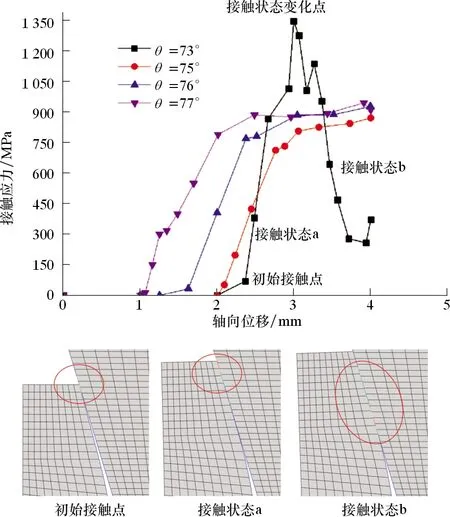
图4 不同锥面倾角下最大接触应力与轴向位移的关系曲线Fig.4 Relationship between maximum contact stress and axial displacement with different cone angles

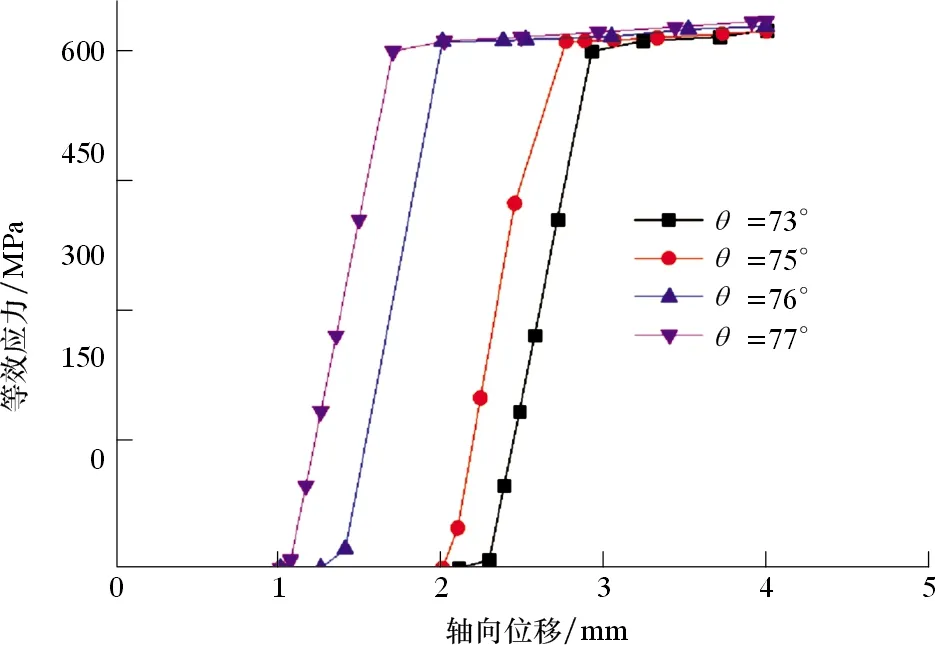
图5 不同锥面倾角下最大等效应力与轴向位移的关系曲线Fig.5 Relationship between maximum equivalent stress and axial displacement with different cone angles

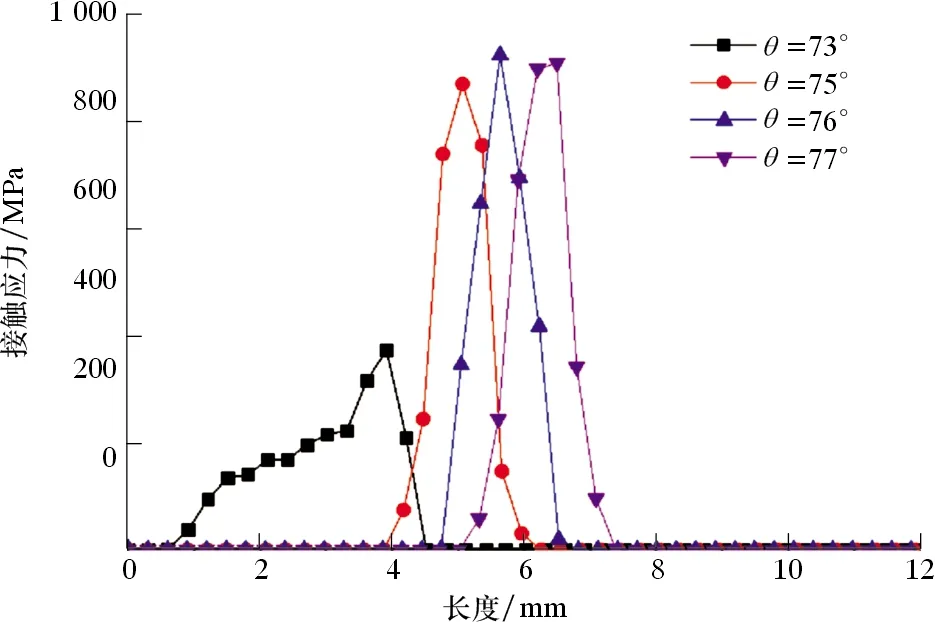
图6 不同锥面倾角下接触应力沿路径A→B的分布规律Fig.6 Distribution of contact stress along path A→B with different cone angles

从图4可以看出，随着轴向位移的增加，接触应力刚开始为0，主要原因是初始间隙的存在，密封面还未接触上。随后接触应力逐渐增加，且呈线性增加趋势，而后接触应力缓慢增加，其中密封锥面倾角为75°、76°和77°时，接触应力变化趋势基本一致，其中初始接触点的不同主要原因是锥面倾角的改变，导致接触部位发生了变化，从而影响图4中不同倾角时密封面初始接触时的位移值。当锥面倾角为73°时，接触应力先增加后减小，然后再增加，其主要原因是密封面接触过程中，接触状态发生了改变，具体过程如图4所示。因为锥面倾角θ过小时，初始接触部位位于外螺纹密封面的端部，随着轴向位移的增加，接触应力逐渐增加，接触面积也逐渐增大，对应图4中的接触状态a；当轴向位移到达图4所示的接触状态变化点时，密封接触状态发生改变，接触面由A点向B点移动，此时，接触面积急剧增加，导致接触应力快速下降，对应图4中的接触状态b，因此设计时需避免这种接触状态不稳定的情况。

从图5可以看出，不同倾角下等效应力随轴向位移的增加表现为先呈线性增加趋势，然后呈缓慢增加趋势并逐渐趋于水平，主要原因为初始变形阶段，密封结构最大等效应力小于材料的屈服应力，应力和应变表现为线性关系。当轴向位移过大时，密封接头最大等效应力大于材料的屈服应力，材料开始发生塑性变形，故最大等效应力呈缓慢增加趋势，与材料的本构模型相符合。当锥面倾角为73°、75°、76°和77°时，材料达到屈服所需的过盈量分别为0.77、0.76、0.75和0.63 mm；材料达到屈服时，所对应的接触应力分别为1 004.0、711.6、404.8和548.7 MPa。通过上述分析，在本组设计参数下，75°锥面倾角、0.76 mm的过盈量为最佳设计参数，满足密封设计准则。

从图6可以看出，73°锥面倾角对应最大接触应力为373 MPa，但是密封长度相比其他锥面倾角要长，其余3种锥面倾角对最大接触应力和密封面长度影响不大，只是对密封位置有影响，对密封性能影响不大。

4.2.2 密封球面弹性体厚度对密封性能的影响

当密封锥面倾角θ=76°，密封球面半径R=25.4 mm，密封球面弹性体厚度L分别为1.50、2.00、2.74和3.50 mm时，最大接触应力和最大等效应力与轴向位移的关系曲线分别如图7和图8所示。当轴向位移为4 mm时，接触应力沿路径A→B的分布规律如图9所示。

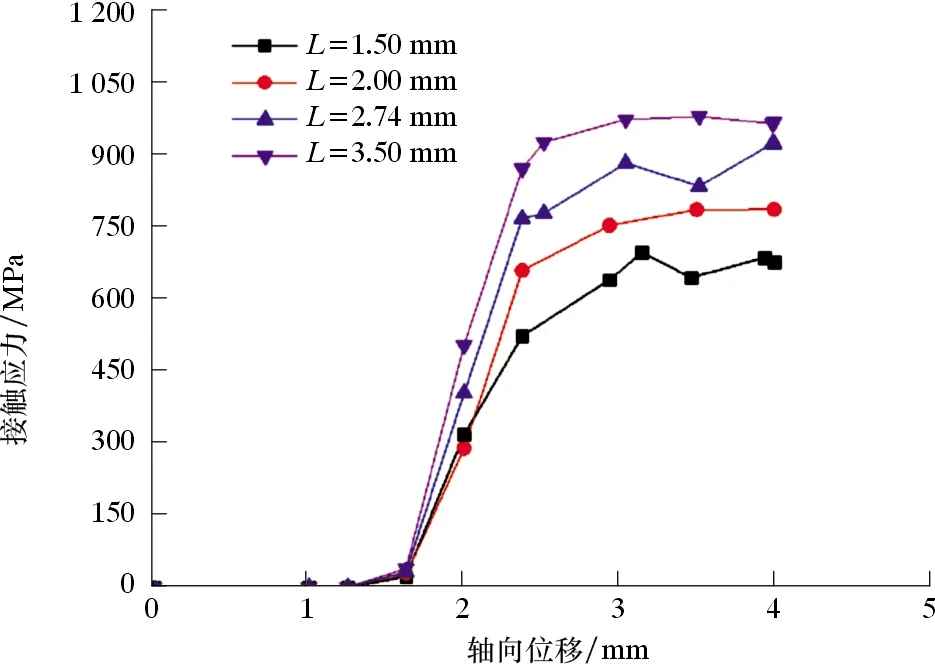
图7 不同弹性体厚度下最大接触应力与轴向位移的关系曲线Fig.7 Relationship between maximum contact stress and axial displacement with different elastomer thicknesses

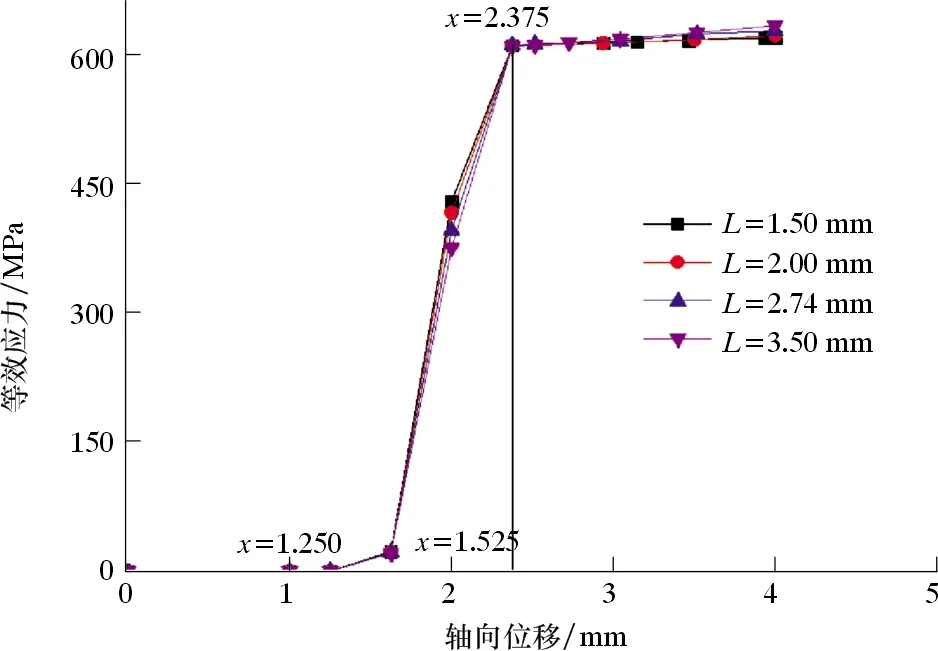
图8 不同弹性体厚度下最大等效应力与轴向位移的关系曲线Fig.8 Relationship between maximum equivalent stress and axial displacement with different elastomer thicknesses

图9 不同弹性体厚度下接触应力沿路径A→B的分布规律Fig.9 Distribution of contact stress along path A→B with different elastomer thicknesses

从图7可知：随着轴向位移的增加，接触应力刚开始为0，主要原因是初始间隙的存在，密封面还未接触上；轴向位移在1.62～2.37 mm之间，接触应力呈线性增加趋势；轴向位移超过2.37 mm后，接触应力缓慢增加。随着密封球面弹性体厚度的增加，相同轴向位移下，厚度越大，接触应力越大，其主要原因为弹性体厚度的增加导致接触面刚度增加，从而接触应力增大。

从图8可以看出：不同密封球面弹性体厚度下，等效应力随轴向位移的增加先呈线性增加趋势，然后缓慢增加，主要原因为初始变形阶段，密封结构最大等效应力小于材料的屈服应力，应力和应变表现为线性关系；当轴向位移超过2.375 mm后，密封结构最大等效应力大于材料的屈服应力，材料开始发生塑性变形，故最大等效应力呈现缓慢增加趋势，与材料的本构模型相符合。在相同过盈量下，密封球面弹性体厚度对最大等效应力的影响不大。

从图9可以看出，随着密封球面弹性体厚度的增加，最大接触应力呈增加趋势，同时密封长度也呈增加趋势。故通过上述分析，弹性体厚度L可选择3.5 mm，材料发生屈服时的过盈量为0.75 mm，此时最大接触应力为872 MPa，满足密封设计准则。

4.2.3 密封球面半径对密封性能的影响

当密封锥面倾角θ=76°，密封球面弹性体厚度L=2.74 mm时，不同密封球面半径下最大接触应力和最大等效应力与轴向位移的关系曲线分别如图10和图11所示。当轴向位移为4 mm时，接触应力沿路径A→B的分布规律如图12所示。

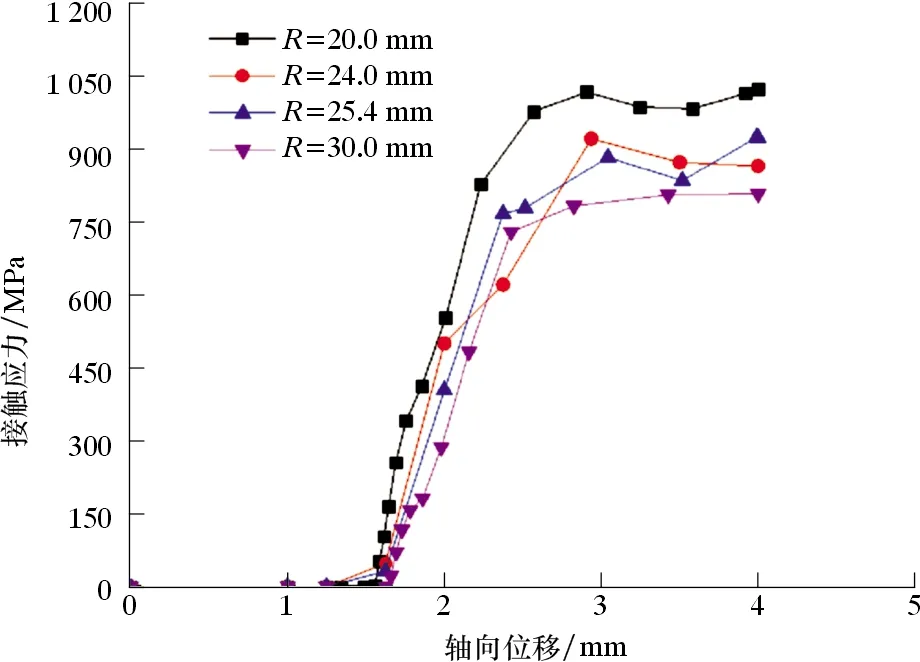
图10 不同球面半径下最大接触应力与轴向位移的关系曲线Fig.10 Relationship between maximum contact stress and axial displacement with different sphere radius

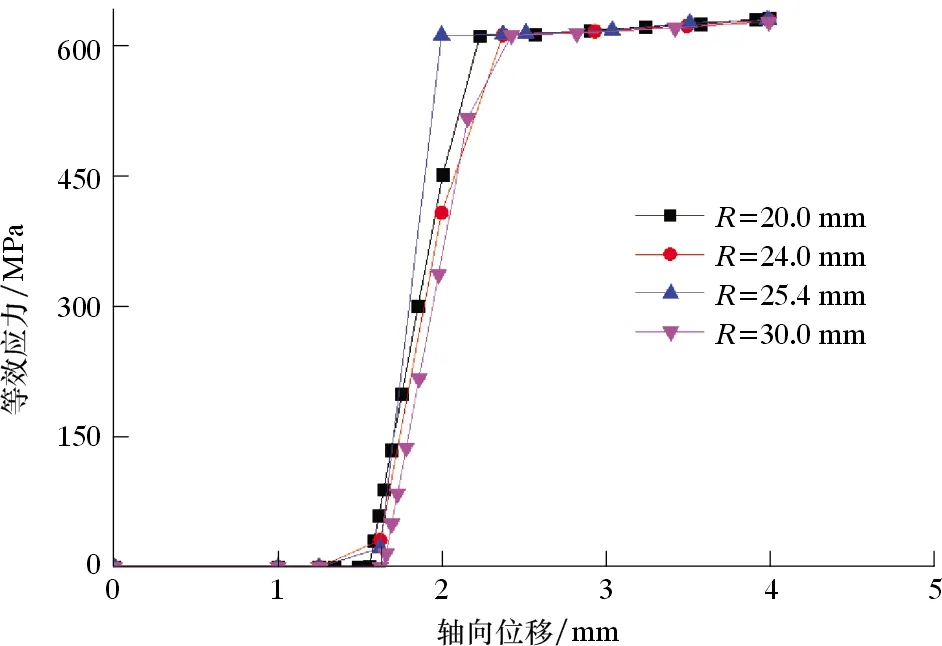
图11 不同球面半径下最大等效应力与轴向位移的关系曲线Fig.11 Relationship between maximum equivalent stress and axial displacement with different sphere radius

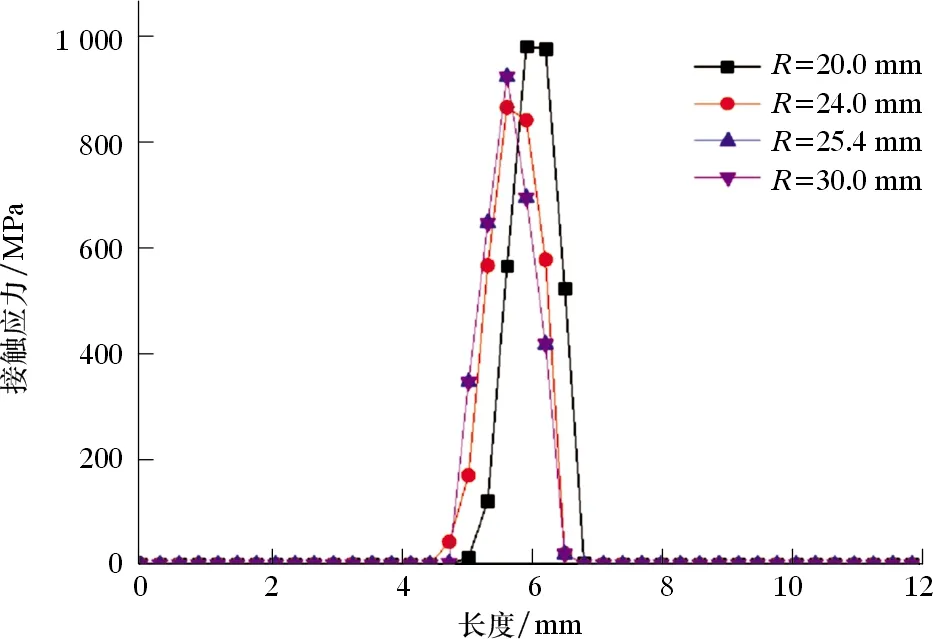
图12 不同球面半径下接触应力沿路径A→B的分布Fig.12 Distribution of contact stress along path A→B with different sphere radius

从图10可知：随着轴向位移的增加，接触应力刚开始为0，主要原因是初始间隙的存在，密封面还未接触上；然后接触应力呈线性增加趋势，超过一定轴向位移后，接触应力缓慢增加；随着密封球面半径的增加，在相同轴向位移下，接触应力逐渐增加；当密封球面半径为20 mm，轴向位移为2.9 mm时，接触应力最大，其值为1 018 MPa。

从图11可以看出，不同密封球面半径下，等效应力随轴向位移的增加先呈线性增加趋势，然后缓慢增加，主要原因为初始变形阶段，密封结构最大等效应力小于材料的屈服应力，应力和应变表现为线性关系。当球面半径分别为20.0、24.0、25.4和30.0 mm时，材料发生屈服时的过盈量分别为0.68、0.75、0.38和0.76 mm，该过盈量下对应的接触应力分别为828、622、404和730 MPa。

从图12可以看出，密封球面半径对密封长度的影响不大。通过上述分析，密封球面半径可选择20.0和30.0 mm，过盈量分别为0.68和0.76 mm，该过盈量下对应的接触应力分别为828和730 MPa，满足密封设计准则。

5 有限元分析与室内试验

基于上述设计，本文选取密封锥面倾角75°、密封球面半径20 mm、密封球面弹性体厚度3.5 mm及过盈量0.7 mm作为最优设计参数，并建立模型进行仿真分析，结果如图13和图14所示。

从图13可以看出，密封接头最大等效应力位于外螺纹端弹性体区域，最大值为559.39 MPa，小于材料的屈服强度，强度满足设计要求。从图14可以看出，密封结构的最大接触应力为771.58 MPa，大于10倍设计压力，满足密封设计准则。因此优选的设计参数均能满足设计需求。

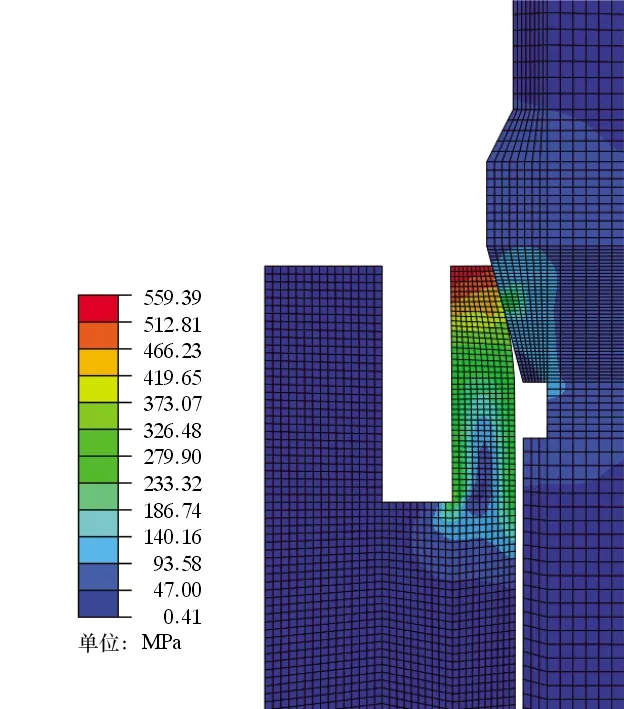
图13 密封接头等效应力云图Fig.13 Cloud chart of equivalent stress of seal joint

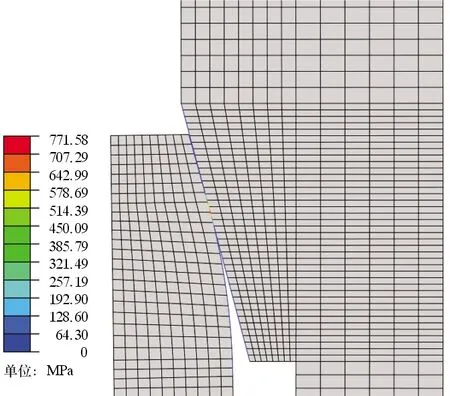
图14 接触应力沿路径A→B的分布规律Fig.14 Distribution of contact stress along path A→B

基于上述设计参数，加工试制了一套井下安全阀，并进行了工作压力70 MPa的整体水压试验，以验证设计和仿真模拟的正确性。水压试验分3个阶段进行加压，分别为27.6、41.4 和70.0 MPa，最后在70.0 MPa时稳压10 min，无渗漏。室内水压试验压力曲线如图15所示。

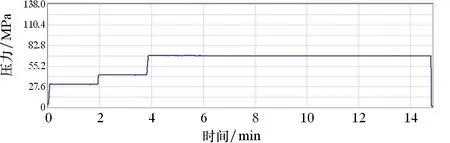
图15 室内水压试验压力曲线Fig.15 Indoor hydrostatic test pressure curve

6 结 论

(1)通过对井下安全阀螺纹密封结构的设计、参数优化和室内试验，验证了有限元仿真模型的正确性以及结构参数设计的合理性。设计的螺纹密封结构能满足井下安全阀70 MPa的密封要求。

(2)73°锥面倾角会导致密封面接触状态不稳定变化，引起接触应力存在突变，因此应避免采用该倾角的设计；在相同过盈量下，密封球面弹性体厚度对最大等效应力影响不大，对接触应力有提高作用；密封球面半径对密封长度的影响不大。

(3)密封锥面倾角为75°，密封球面半径为20 mm，密封球面弹性体厚度为3.5 mm，过盈量为0.7 mm，可满足密封设计要求。