基于ConvGRU深度学习网络模型的海表面温度预测
张雪薇,韩震,2*
(1.上海海洋大学 海洋科学学院,上海 201306;2.上海河口海洋测绘工程技术研究中心,上海 201306)
海表面温度是海洋环境主要要素之一,在气象学、航海、渔业和海洋环境保护等领域起着重要的作用[1]。如何有效地挖掘其信息,并对其时序关系和空间特征进行提取,是海洋科学领域亟待解决的问题[2-3]。对于海表面温度数据时间尺度的预测,传统时间序列预测方法大多忽略了自然地理位置中数据的空间分布信息,且在处理海量海表面温度数据方面存在欠缺[4-5]。海表面温度数据具有时间性、空间性和多维性,可通过挖掘其数据各要素间的关联性和时空尺度变化下的规律性,更好地认识海洋各环境要素耦合下的本质特征。
海洋预测模型通常有两类方法:一类是数值方法,另一类是数据驱动方法。前者利用动力学方程和热力学方程建立预测模型;后者使用统计或机器学习方法,从数据中学习建立预测模型。随着深度学习技术的快速发展[6],建立准确的模型对海表面温度进行预测具有重要的研究意义。2007年,Garcia-Gorriz等[7]利用人工神经网络(ANN),对地中海西部海表面温度的季节和年际变化进行了预测,预测效果较好。2017年,Zhang等[8]利用LSTM模型对海表面温度进行了预测,其网络架构由LSTM层和全连通密集层组成,并以中国沿海海域为例验证了该方法的有效性。同年,Jiang 等[9]分析了温度、盐度和地理位置对温跃层的影响,提出了一种改进的基于熵值法的跃层选择模型,该模型能够有效地预测温度的变化。2019年,Xiao等[10]在东海利用36年星载海表面温度数据建立了LSTM模型,该模型对短期和中期海表面温度场的日预测效果较好。2020年,Xu等[11]提出了M-LCNN预测模型,利用小波变换对时间序列进行分解和重构以预测海表面温度多个时间尺度的序列变化。同年,He等[12]构建了一个采用局部搜索策略的SSTP模型,该模型适用于长时间序列的海温数据预测。以上基于深度学习的海表面温度预测方法均存在一些不足:如参数的数据量过少,不适用于处理海量的海洋数据;大多忽略了自然地理位置中的区域分布信息,导致区域信息的丢失;没有很好地将时间特征和空间特征相结合,故很难同时达到模型的预测精度和信息特征提取的准确度。
循环神经网络(recurrent neural networks,RNN)作为提取动态时间序列的网络,具有对数据进行选择性记忆的特点[13],可以将上一层的输出作为下一层的输入[14],通过在不同区域上增加卷积操作,得到时序关系和空间特征,解决了传统方法中数据空间分布信息丢失的问题。基于RNN扩展算法和卷积神经网络(CNN)相结合的ConvGRU深度学习网络模型,通过在不同的区域上叠加卷积操作,能够得到时序关系和空间特征,在信息挖掘的基础上,更好地预测其未来的变化规律。ConvGRU模型在视频目标检测、多目标跟踪和医学等方面应用广泛[15-17]。该模型解决了传统时间序列网络未能将时间性与空间性很好地结合、区域信息丢失及批量处理海洋大数据能力差的问题。本研究中,以西北太平洋部分海域为研究区域,开展了基于ConvGRU循环神经网络模型的海表面温度预测分析,以期提高海表面温度的预测精度。
1 相关模型
1.1 RNN模型
循环神经网络RNN采用定向循环,使得隐藏节点定向连接成环,这样的内部结构有利于信息传递,可以将同层间不同的神经元进行连接,并且同一时间的网络层可以共享权值参数。RNN的输入和输出数据均为向量序列,可以较好地体现数据的时间序列性。
hk=fh(Wihxk+Whhhk-1+bh)。
(1)
其中:hk为k时刻RNN隐层的状态向量;Wih为从输入层到隐层的连接矩阵;Whh为隐层相邻时刻之间的连接矩阵;xk为k时刻输入样本;bh为偏置向量;fh为非线性激活函数,在RNN中,fh通常为sigmoid或tanh函数。
ok为RNN网络输出,其计算公式为
ok=f0(Wh0hk+b0)。
(2)
其中:Wh0为隐层到输出层的连接矩阵;b0为输出层的偏置向量;f0为非线性激活函数。
RNN可以得到时间序列特征,但当网络层增加时,会因BPTT(back propagation through time)而导致梯度消失,从而无法获得相隔时间比较长的数据间的相关性。GRU作为RNN的变体,只要在GRU中增加卷积操作就可以解决这个问题。
1.2 ConvGRU模型
ConvGRU模型是RNN扩展算法和卷积神经网络的结合[18]。ConvGRU的核心思想是将矩阵运算加上卷积操作,既能利用GRU得到时序特征,又能利用卷积计算提取空间特征。ConvGRU模型采用门结构控制信息流动,权重的一部分放到了卷积核内,另一部分放入循环层的循环核。
ConvGRU模型计算公式为
Zt=σ(Wxzxt+WhzHt-1),
(3)
Rt=σ(Wxrxt+WhrHt-1),
(4)
Ht′=f[Wxhxt+Rt∘(WhhHt-1)],
(5)
Ht=(1-Zt)∘Ht′+Zt∘Ht-1。
(6)
其中:Zt为更新门;Rt为重置门;Ht′为候选门(记忆状态);x为卷积操作;∘为哈达玛积;xt为输入;f为非线性激活函数;σ为sigmoid激活函数;H和W为输入张量的高和宽。
2 海表面温度预测模型的构建
2.1 研究区域和数据
选取西北太平洋10°~30°N、130°~160°E的海域为研究区域。研究数据来自美国国家海洋和大气管理局(NOAA)的OISST(optimum interpolation sea surface temperature)的最优插值OI(optimum interpolation)产品(https://climatedataguide.ucar.edu/climate-data)。OISST原始数据[19]来源于卫星数据和现场平台(船舶和浮标)的海表面温度(sea surface temperature,SST)观测数据,是由插值和外推数据创建的空间网格产品,也是目前应用最广泛的再分析数据产品之一。每天的OISST数值误差包含随机误差(random errors,RE)、采样误差(sampling errors,SE)和偏置误差 (bias errors,BE),由于选取数据的时间不同,产生的误差也不同。一个完整的海温图通过插值填补空白产生,该方法包括卫星和船舶观测(参考浮标)的偏差调整,以补偿平台差异和传感器偏差。OISST将船舶数据和浮标数据作为实测数据(船舶-浮标数据的总体差异为0.138 ℃)[20]进行数据的误差分析,浮标的海表温度观测精度各不相同,随机误差通常小于0.58 ℃[21]。全球平均误差为0.38 ℃,在年际尺度上,产品间的全球平均差异约为0.058 ℃[22]。本研究中,训练和验证数据为1999—2019年海表面温度数据,预测数据为2020年海表面温度数据,其空间分辨率均为1°。
2.2 预测模型的总体结构
海表面温度预测模型ConvGRU总体结构如图1所示,其预测的具体步骤包括数据预处理、样本生成器建立与数据筛选、网络模型的建立、预测与存储和模型评估分析。模型结合了卷积神经网络和循环神经网络的特点,并利用样本生成器处理数据,解决了长时间序列遥感数据的批量处理问题;通过对数据进行批量随机训练,提高了训练的效率和可靠性;通过改进模型本身的训练层和样本生成器,提升了预测结果的精度。

图1 预测模型ConvGRU的结构Fig.1 Structure of the prediction model ConvGRU
2.2.1 数据的预处理和样本生成器的建立 选取1999—2019年SST数据构建一个三维数据集。主要过程包括对创建的时间序列文件进行区域选取,重构样本集NC文件,对样本集NC文件增加通道维度,形成样本数据,然后对数据进行归一化处理(图2),其计算公式为

图2 预处理流程图Fig.2 Preprocessing flow chart
xnormalizatin=(x-max)/(max-min)。
(7)
其中:xnormalizatin为海表面温度数据0~1数值内的归一化值;max、min分别为时间步长内海表面温度数据的最大值和最小值;x为时间步长内海表面温度数据的每月网格数据值。
将归一化值作为生成器的标签值,构建标签样本集NC文件,形成标签样本集。将选取区域的样本数据划分为训练数据集和评估数据集,训练数据集为1999—2019年数据,通过训练这些数据来预测2020年,并用2020年数据集进行验证评估。
在样本生成器中批量选取数据进行训练,建立样本训练集生成器。从样本数据中随机选取20个批量数据作为1步,每步包含连续6个特征数据,7步为1轮进行400轮计算。每步包含的连续6个特征数据的时间间隔为1个月,形成样本特征集数据。1个标签日期对应6个月的时间特征数据集,通过标签和单步数据的对应关系,建立与样本特征集数据在时间尺度上对应的标签,形成标签数据。
对于样本验证集生成器,随机选取样本数据中10个批量数据作为1步,建立样本特征集数据和标签数据,7步为1轮,进行400轮计算。
在样本生成器中,输入5个维度的样本数据,分别为批量大小、连续时间尺度、纬度值、经度值和通道大小;目标数据输出维度分别为标签数据中的批量大小、纬度值、经度值和通道大小4个维度,以确保用6个连续的时间序列输出1个时间序列的预测效果。
2.2.2 预测模型的建立 预测模型ConvGRU各层参数见表1,主要建立步骤如下:

表1 ConvGRU模型各层参数Tab.1 Parameters of each layer of ConvGRU model
1)将预处理过的数据进行输入,分别将样本数据和标签数据输入到ConvGRU层,通过5层的ConvGRU 2D叠加,建立时序关系。本研究中使用多个ConvGRU层,每层过滤器个数为50,卷积核大小为7×7,每层ConvGRU均带有Dropout内处理层,Dropout可以在每次迭代时随机更新网络参数。在每ConvGRU层,将Dropout值设为0.5,以减少过拟合发生的次数。
2)在每个ConvGRU 2D层后加入一个正则化层(Batch normalization),使得处理海表面温度数据时,调整参数过程简洁,减少对样本数据初始化要求。
3)在ConvGRU 2D层计算后,加入2个Conv2D层进行优化,并将多维计算结果进行2D输出。第一个Conv2D的过滤器个数为50,卷积核大小为7×7;第二个Conv 2D的过滤器个数为1,卷积核大小为7×7。
对建立好的样本生成器中的批量数据进行训练,并利用Keras建立多层ConvGRU模型,获取时空相关性,将训练好的模型进行模型存储。
2.2.3 数据的预测与存储 根据2020年预测数据,建立基于预测每月海表面温度数据的预测样本生成器。随机选取预测样本数据中12个批量数据作为1步,建立样本特征集数据和标签数据,7步为1轮,进行15轮计算,对预测好的模型按月进行参数存储输出。
以npy文件进行训练结果输出,将输出的四维npy预测文件去除通道这一维,并按预测的总个数、纬度值、经度值进行三维重构NC文件,然后进行反归一化操作实现对预测数据的还原。对预测的时间点求平均值,从而形成包含纬度和经度的三维NC文件,最后对结果进行投影输出。
2.2.4 模型评估分析
1)训练模型。在样本训练过程中,利用均方根误差(root mean squared error)和准确率(precision)对训练结果进行评估,其计算公式为
(8)
其中:ERMS为均方根误差,是海表面温度训练值与标签值间差值平方和的平均值(℃);yactual为海表面温度数据的标签值;ypred为海表面温度数据的训练值(℃);n为选择区域的宽和高的乘积。
P=2TP/(TP+FP+FN)×100%。
(9)
其中:P为预测正确的概率(准确率);TP为真正例,即正例的数据点被标记为正例;FP为假正例,即反例的数据点被标记为正例;FN为假反例,即正例的数据点被标记为反例。
ConvGRU模型在预报时,ERMS值越小,代表训练和验证效果越好,而P则相反,P值越大,代表模型的训练和验证效果越好,在训练模型时,可通过分析这两个指标判断模型训练的效果。
2)预测模型。在预测样本生成器中,对15轮数据进行反归一化计算,形成预测数据,并对这些预测数据求平均值,与原始数据进行绝对差值计算,其计算公式为
(10)
其中:DMA为平均绝对误差(mean absolute deviation),是海表面温度预测值与真实值间差值绝对值的平均值(℃);yactual为海表面温度数据的真实值(℃);ypred为海表面温度数据的预测值(℃)。
(11)
其中:AP为海表面温度预测值与真实值间的精度值(prediction accuracy),其值越大,代表模型的预测性能越好,反之,则预测性能越差;n为预测区域宽和高的乘积。
3 海表面温度模型的预测结果
3.1 模型训练结果
用ConvGRU模型进行了400轮训练,模型训练结果见表2。通过对模型训练结果分析发现:ConvGRU模型训练集的均方根误差、准确率平均值分别为0.044 9 ℃、99.69%,最佳值分别为0.042 3 ℃、99.72%;验证集的均方根误差、准确率平均值分别为0.045 2 ℃、99.64%,最佳值分别为0.039 0 ℃、99.70%,总体上可以看出,ConvGRU模型的训练结果较好;模型训练完后,再对其训练结果模型进行评估,发现其测试集的均方根误差、准确率平均值分别为0.047 8 ℃、99.60%,最佳值分别为0.045 4 ℃、99.59%。

表2 模型结果评估表Tab.2 Table of the model result evaluation
3.2 模型预测结果
在预测样本生成器中,对15轮数据进行反归一化计算,形成预测数据,对预测值进行评估,并与ConvLSTM模型预测值进行比较(表3)。对ConvGRU模型进行多轮精度计算,发现6月的平均绝对误差最小,为0.102 9 ℃,与之对应的精度值也最高,为98.39%;作为常用的机器学习预测模型ConvGRU,比传统预测模型ConvLSTM具有更高的预测精度和泛化能力,ConvLSTM模型全年平均绝对误差的平均值为0.583 7 ℃,预测精度的平均值为96.19%,而ConvGRU模型的全年平均绝对误差的平均值为0.379 3 ℃,预测精度的平均值为97.31%,ConvGRU模型的各项指标明显好于ConvLSTM模型。
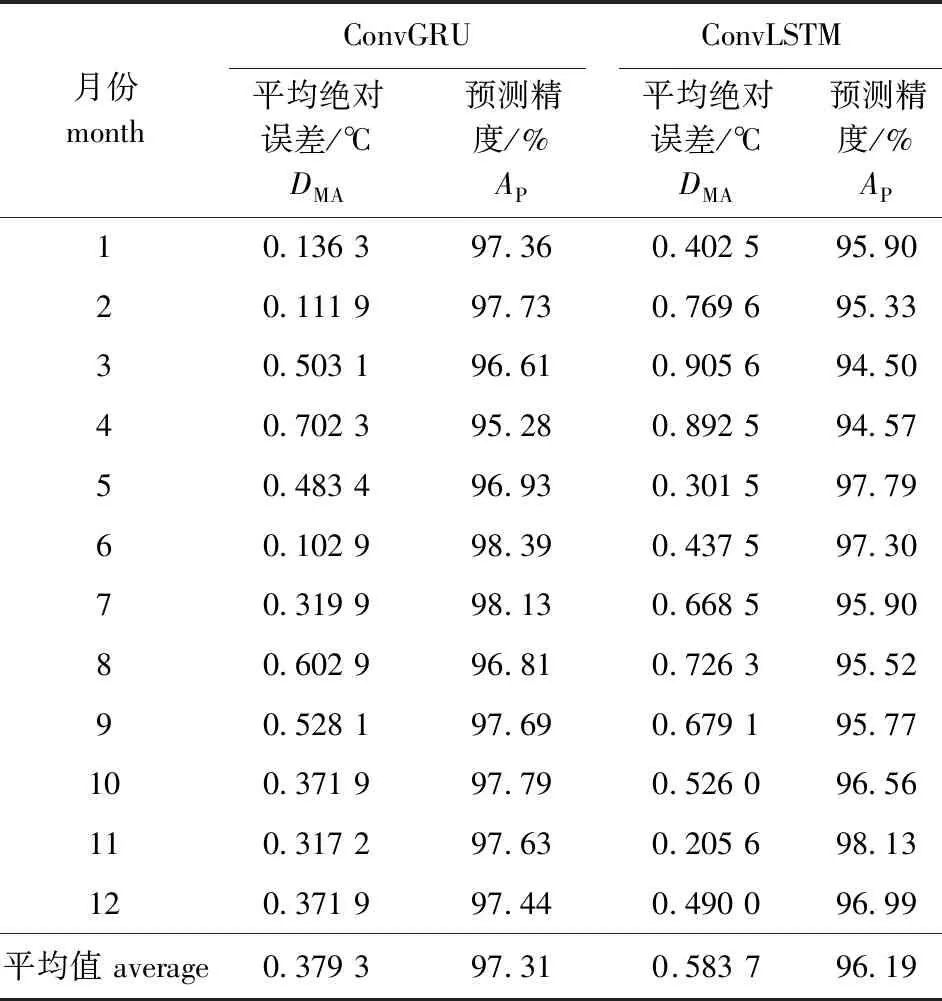
表3 预测值评估表Tab.3 Table of the predicted values evaluation
通过分析2020年12个月的连续变化,可以发现其预测变化的连续性较好,表明ConvGRU模型可以很好地预测海表面温度的时空特征变化。从图3的真实值可以发现,研究海域1—4月的海表面温度变化情况稳定,为19.7~29.1 ℃;5月海表面温度开始升高,最高温度上升1 ℃,5—6月的海表面温度范围为22.2~30.6 ℃;7—9月为全年中海表面温度最高的时段,其变化范围为27.9~30.9 ℃,其中8月为2020年海表面温度最高的时段,为28.6~30.9 ℃;10—12月海表面温度为22.8~30.5 ℃。ConvGRU模型在2020年1—12月显示的预测结果与真实值匹配度较高,总体变化趋势与真实值吻合。
由于原始数据的分辨率问题,在预测海表面温度的细节变化规律方面还存在一些误差。海表面温度预测图(图3)因使用了克里金插值,也会对视觉精度产生影响。为了更好地说明预测模型在研究海域的预测精度,将2020年真实值和预测值的平均值进行了比较(图4),结果显示,实测值曲线和预测值拟合曲线吻合程度较好。

图3 2020年海表面温度真实值与预测值的比较Fig.3 Comparison of actual value with predicted value of SST in 2020

图4 2020年海表面温度真实值与预测值平均值的比较Fig.4 Comparison of actual average value with predicted average value of SST in 2020
4 讨论
4.1 模型的精度比较
对于海表面温度时间尺度的预测,通常使用的传统时间序列预测方法仅适用于处理少量站点的海洋数据,而且不同的海表面温度数据使用的模型参数也存在差异,由于参数的数据量过少,不适用于处理海量的海洋数据。ConvGRU模型利用样本生成器进行训练,可以较好地解决传统预测模型在训练中由于数据量大而无法训练的问题。ConvGRU模型还可以较好地将时间特征和空间特征结合在一起,从而获得更好的训练效果。本研究中,使用ConvGRU模型预测海表面温度平均绝对误差的平均值为0.379 3 ℃,预测精度的平均值为97.31%,与前人预测海表面温度的模型相比较,ConvGRU模型预测精度明显高于ConvLSTM和CFCC-LSTM模型(精度96.59%)[23]。本研究中,从ConvGRU模型预测值与真实值比较可以看出,ConvGRU模型的预测结果在空间上匹配程度较高,在时间上其预测的连续变化性较强,可以较好地预测海表面温度的时空变化。
4.2 模型对西北太平洋海表面温度的预测效果
海表面温度数据具有体量大、类型杂、时效强、难以辨识和高价值等明显的数据特征。海表面温度数据是海洋水文重要参数之一,开展海表面温度预测研究,对于海洋环境保护具有重要的理论价值和实际意义。从本研究的预测结果可以看出(图3):研究区域1—6月的海表面温度为19.7~29.8 ℃;7—9月海表面温度为27.1~29.9 ℃,其中8月海表面温度最高,为27.5~29.9 ℃;10—12月海表面温度开始下降,最低降到23.1 ℃左右,12月海表面温度为23.1~29.5 ℃,10—12月海表面温度为23.1~29.9 ℃。预测的结果在时空变化规律上符合前人得出的西北太平洋区域历年海温年际变化规律[24]。
本文中构建的ConvGRU深度学习模型是对西北太平洋海表面温度预测的尝试。该模型的优势之处是可以利用空间和时间特征之间的内在联系,强化自然位置的区域分布信息,可提高模型的区域性效果和整体适用性效果。本研究中,在现有的海洋信息探测深度学习算法基础上,面对海洋环境信息大数据特征,利用样本生成器建立了海洋环境信息样本库和适应高维度、多尺度、非平稳特征的区域性海洋环境信息神经网络预测模型。
综上所述,利用ConvGRU模型预测海表面温度是切实可行的,且在研究区域具有较高的预报准确度。与其他方法相比,该网络模型的平均绝对误差和预测精度均有明显改善,能够较好地预测海表面温度的变化,为西北太平洋海域的海表面温度预测提供了一种新的思路。
5 结论
1)ConvGRU模型利用RNN的时间性和CNN的空间性,将海表面温度数据的时间和空间特征相结合,为建立海洋环境信息样本库及建立适应高维度、多尺度、非平稳特征的海表面温度神经网络预测模型提供了一种可行性方法。
2)利用ConvGRU模型预测海表面温度是切实可行的,且在研究区域具有较高的预报准确度。
3)ConvGRU深度学习预测模型在一定程度上解决了传统时间序列网络模型在时间性与空间性结合上不足,以及批量处理海洋环境要素大数据能力不足的问题。但是在影响海表面温度预测的要素中,还存在其他环境影响因子,如盐度、风速等。另外,数据选取不同的时间尺度也会影响其预测精度。在以后的研究中,可加入多参数进一步优化模型,提高海表面温度预测精度。

