双干涉仪系统的交叉协同无源定位误差分析
李钊
(中国电子科技集团公司第二十九研究所 四川省成都市 610036)
1 引言
随着技术的发展,电子接收系统对目标辐射源快速定位法在实际的设备上正逐步得到应用,但定位的精度和收敛时间有待提高。目前的单系统无源定位一般是运用电子接收系统在运动中接收外界目标辐射源的信号,通过电子接收系统内部的信号处理算法测量得到一定的测量值,然后根据一定的时间上积累的足够多的测量值信息,进行算法收敛来估计出目标辐射源的位置信息。
一般对目标辐射源位置的测量分为比幅测向和干涉仪测向。比幅测向是通过比较相邻天线所接收的同一个信号信息,在电子接收系统内部经过相互独立的射频通道来比较不同射频通道采集的信号强度值,达到测量目标辐射源的位置信息,测向时间为瞬时,但测向精度比较粗;干涉仪测向是通过接收天线接收的辐射源信号达到天线口面的相位差,通过电子接收系统内部鉴相器来解算目标辐射源的位置信息,达到测量目标辐射源的位置信息,测向时间需要一定的时间进行收敛,但测向精度比较高。
目前要对目标辐射源实现精确的定位一般都选择干涉仪测向,但是干涉仪测向需要一定的时间进行收敛,而且定位的精度和电子接收系统运动的轨迹以及系统内部积累测量值信息数量有很大关系。本文采用双系统对同一目标实现无源定位,大大的缩减了电子接收系统所需要运动时间,以及更短的时间就能实现精确的定位。
2 干涉仪无源定位
2.1 干涉仪定位原理
干涉仪无源定位是利用辐射源发射出来的电磁波在干涉仪接收天线基线上形成的相位差来确定辐射源的位置信息,具有测向精度高和实现原理简单等特点,是实现对辐射源高精度测向优选技术体制,在干涉仪天线阵中采用短基线实现覆盖空域的无模糊测向,采用长基线实现高的测向精度。
干涉仪测向是一种成熟的测向体制,相比于比幅测向和时差测向体制,它耗费的硬件资源较大,但其最大的优势是能够兼顾天线阵的尺寸和测向精度,在较小的平台上可以实现高精度测向。干涉仪无源定位原理示意图如图1 所示。

图1:单系统无源定位
辐射源信号相位差和入射波的角度θ 可以根据公式得出:

其中,干涉仪基线长度为D,信号传播速度为c,信号波长为λ,传输波程差为∆D。

2.2 定位误差分析
对辐射源信号相位差求偏导,相位差增量∆根据公式得到:
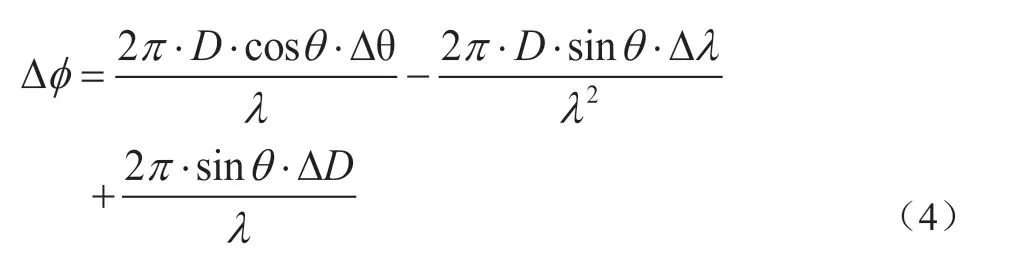
基线长度误差,在实际上可控制到0.1mm 量级,对相位差的影响仅仅只有1~2°,可忽略不计;一般频率测量仪器的精度可达到1MHz 以上,折算后,对相位差的影响仅仅只有1~2°,也可忽略不计。
因此,只剩下角度误差∆θ 的影响,由公式得到:

可转换为:

目标定位误差的来源主要是有天线单元之间的相位误差,接收系统内部接收通道的相位误差和相位的测量误差产生。
3 传统的单系统无源定位
传统的单系统干涉仪定位主要采用测向-交叉定位法,测向-交叉定位法是无源定位中应用最多的一种,可以同时对多个目标进行测向定位,且定位时间和定位精度主要由系统测向精度和目标与接收系统相对位置决定。测向-交叉定位法需要接收系统运动较长的距离,以保证有足够大的测向交会角,就能够达到比较高的测向精度,因此该方法的定位速度相对较慢,通常在几分钟以上。
多普勒频率差定位法是通过测量目标与观测站之间的相对运动引起的多普勒频移提取目标的距离信息,具有定位速度快的优点。但这类方法对频率的测量精度提出了很高的要求,且要求对方频率稳定,目前很难实现。
相位差变化率定位法主要通过在系统上安装干涉仪天线阵获得辐射源信号的相位变化率信息来计算辐射源的距离,再利用精测角系统获得的目标方位信息即可实现对目标的实时定位。该方法比传统的只测角测距法性能高很多,但代价是增加了系统复杂度和难度。该方法通常采用多基线干涉仪阵列,利用短基线干涉仪进行精确测向,利用长基线干涉仪测量辐射源信号的相位变化率。
短基线干涉仪定位采用相位差变化率干涉仪测量定位体制实现对目标的测量定位,其基本原理是相位角测向,就是利用系统中不同接收支路之间的相位差来获得目标的方向角信息,具有测向定位精度高的优点,但是不可避免的存在测向定位模糊的问题。
长基线干涉仪定位采用相对较长的基线,同样采用相位差变化率干涉仪测量定位体制实现对目标的测量定位,原理也是相位角测向,但是和短基线相比,因为有相比短基线干涉仪而言拥有较长的基线,可以实现对目标的单脉冲测距,而且对目标的位置和运动状态没有限制,结合测向角度信息可以得到目标的位置,是实现固定无源定位的重要方法。
4 双系统无源定位
4.1 双系统无源定位原理
双系统测向交叉定位是指利用两个接收系统得到的目标相对于自身的测向线在空间中相交从而确定目标的位置。不管是在二维空间还是三维空间,最少只要有两条不同载机的测向线就可以进行交叉定位而确定目标的位置。但是在二维空间中,每个接收系统确定一条测向线只需要一个角度即可,而在三维空间中,确定每条测向线需要两个角度。因此多系统测向交叉定位为立体定位问题,相对复杂得多。
协同干涉仪定位包括双系统协同定位和多系统协同定位两种。双系统协同定位拟采用测向-交叉定位法,该方法对双系统的同步控制精度并没有很高的要求,在工程上实现的难度相对较小,但其定位精度稍差。多系统协同定位拟采用时差定位法,该方法具有定位精度高的优点,但是它对载机的自定位精度、机间链路和载机之间的同步控制等方面提出了很高的要求,系统实现较为复杂。
若两个电子接收系统协同对辐射源进行定位时,两个电子接收系统工作在主从模式下,通过数据链周期性将主系统位置信息和运动方向信息传送给副接收系统。其中副系统根据主接收系统的位置信息和运动信息选择可实施协同定位的目标,将其方位信息和工作参数信息发送至主系统。主系统将副系统发送的目标参数与自己侦收到的目标辐射源参数进行匹配,对确定为同一目标的信号进行定位计算。由于两个系统的地域不同,所侦收到的目标以及目标对应的批号均不同,因此在双系统协同定位时需要副系统将符合双系统定位条件的目标通过数据链发送至主系统,主系统根据工作参数对目标进行匹配并定位。
双系统交会定位的基本原理与单系统多点交会定位的原理相同,两个接收系统同时测量目标的方位角,然后利用三角定位原理实现对目标的定位,双系统交会定位原理的示意图如图2 所示。
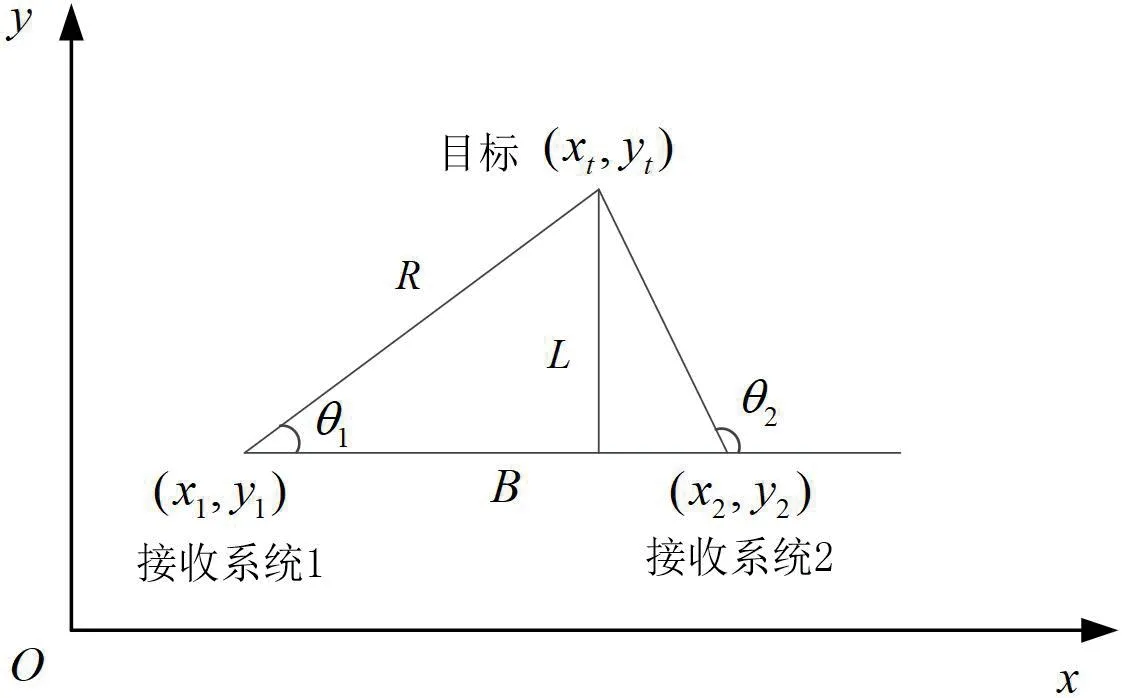
图2:双系统交会定位原理图
以两个接收系统之间的连线作为x 轴,建立直角坐标系xoy。设观测站1、2 的位置坐标分别为(x, y)、(x,y),接收系统测量得到的目标方位分别为θ、θ,目标的位置坐标为(x, y)。由几何关系可以得到:

求解该方程组可以得到目标的位置坐标为:

可见,若已知接收系统的位置(x, y)、(x, y)以及方位测量值θ、θ有关,即可利用上式计算获得目标位置(x,y)。
4.2 定位误差分析
根据双接收系统交会定位的表达式(14),接收系统的自定位误差以及方位测量误差都会影响协同定位的精度。对表达式(14)求微分,有:
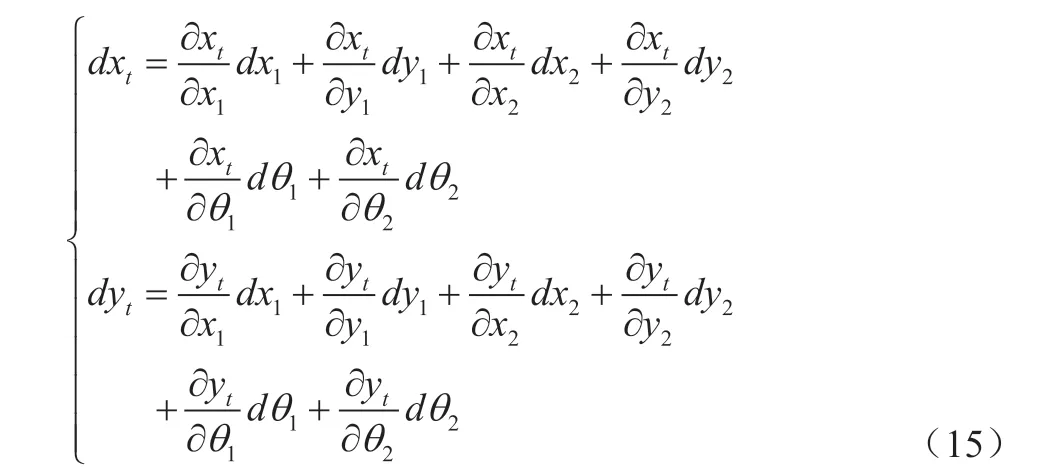
考虑到两个接收系统之间连线与x 轴平行,则有x-x=B,y=y成立,设目标到两个观测站连线的垂直距离为L,则定位误差可以表示为:

对表达式(10)求方差可以:
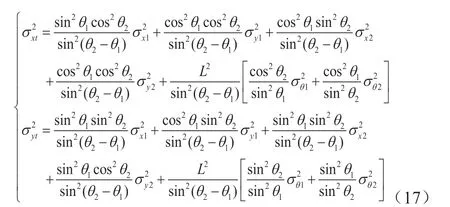
接收系统的自我定位误差都一样,满足表达式:

接收系统的测向误差也一样,满足表达式:

将式(18)、(19)代入式(17),化简后得到定位误差的方差为:

其中R 为目标辐射源与两个接收系统距离的较大者。
5 仿真及分析
根据上述运算验证实际使用的双系统交会定位算法,构建定位场景,对双接收系统交会定位进行仿真。最大接收信号距离300km,设定目标频率3GHz,系统自我定位精度100m,测向精度2°,双系统间隔基线B=150km、250km。
双接收系统定位的典型定位运动态势图如图3 所示。
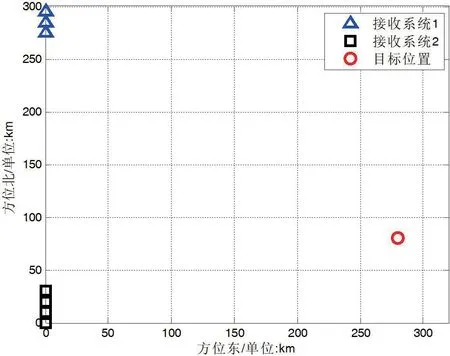
图3:典型定位运动态势图
接收系统1 和接收系统2 以相同的速度和相同的方向对目标进行信号接收以及定位,双接收系统之间的距离相对固定,两者相对目标的位置不断的改变。
5.1 基线150km仿真结果
按照上述仿真条件,当双接收系统基线长度为150km时,仿真结果如图4 所示。
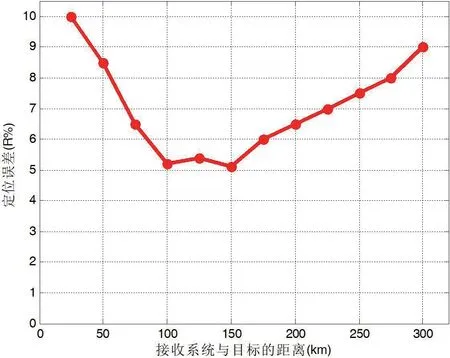
图4:基线150km 定位仿真结果
由仿真结果可以看出,当双接收系统之间的间隔基线为150km 时,对距离在100km ~300km 的地面固定目标定位精度大约为5%R ~10%R,而且定位精度随距离变化起伏很大及其不稳定。
5.2 基线250km仿真结果
按照上述仿真条件,当双接收系统基线长度为250km时,仿真结果如图5 所示。
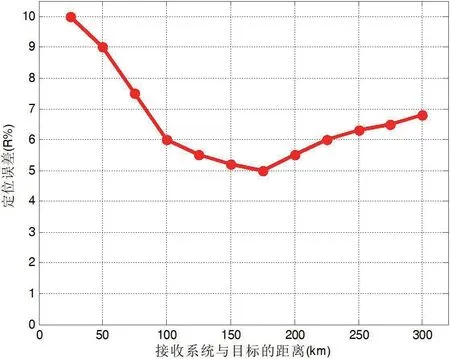
图5:基线250km 定位仿真结果
由仿真结果可以看出,当双接收系统之间的间隔基线为250km 时,对距离在100km ~300km 的地面固定目标定位精度大约为5%R ~10%R,但是定位精度随距离的增加收敛比较稳定。
5.3 仿真分析
从双接收系统的150km 和250km 两种基线长度的仿真结果可以看出,定位误差与目标相对于接收系统的位置有关,增大双接收系统的间距,在相同时间内能够快速提高定位的精度,而在双接收系统间距一定的情况下,若目标距离双接收系统连线的中心较近或较远时,都将使定位误差增大。
6 结论
通过本文的对单一系统运用干涉仪定位的模型和原理分析的基础上,介绍了一种双接收系统运用各自系统内部的干涉仪协同对同一目标进行定位,给出了双接收系统的原理和方法,并对该方法展开模拟实际场景进行仿真分析。 验证结果表明,双接收系统对同一目标进行定位,在定位精度上都远远优于单一系统的定位方法,而且发现当两个接收系统的间隔基线拉得越长时定位的精度越高。采用单系统干涉仪基线定位精度都在10%R ~20%R,而在双系统干涉仪交叉协同定位的精度可提高到5%R ~10%R,而且定位的精度会随着两个系统基线的变长而变高,因此,双接收系统协同定位方法远远优于任何单一系统定位的方法,同时,双接收系统协同定位时尽可能加大两个接收系统间隔基线。

