量子网络抽签系统设计
张盛 孟增辉 左开伟 龚辉
(武警海警学院 浙江省宁波市 315800)
1 引言
抽签由来已久,其应用范围非常广泛,适用于商业、政府、军事以及教育等多个领域的众多应用场景。抽签系统的本质是通过随机抽取的方式保证参与抽签的各方能够以公平的方式获得某种排序。抽签最关键的性能指标是公平性,即保证参与各方获取最大的随机性,且即使有人作弊,也必须付出相应的代价。当前,各类网络抽签系统或软件比较流行,但是,其本质是基于网络安全协议来保证其公平性。换而言之,传统的网络抽签系统的安全性建立在数学密码的基础上。
量子密码是近三十年来兴起的一项新技术,其特点就在于具有理论上的无条件安全特性。与传统的数学密码相比,量子密码的安全优势是毋庸置疑的。其中,量子掷币协议作为量子密码的一个应用分支,可以帮助网络双方在互不信任的前提下,实现一次公平的随机数共享。正因为如此,通过合理的拓展,量子掷币可被用于构建一个公平的网络抽签系统。
2 量子掷币协议概述
掷币协议最初是由Blum 于1981 年提出,两年以后,Bennett 和Brassard 提出了第一个量子掷币协议。虽然,Mayers 等人证明了理想的量子掷币协议是不存在的,但是,跟经典掷币协议相比,量子版本显然具有更高的安全性。一般而言,根据掷币双方的喜好值(0 或1)是否固定,可将量子掷币协议分为强和弱两个类型,固定喜好值的属于强量子掷币,反之则为弱量子掷币。若其中任意一个掷币方的偏好概率高达1,则意味着他(她)可以通过作弊方式得到自己想要的喜好值,且不会被发现。这种情况意味着其中一方可以完全控制协议,即掷币失败。
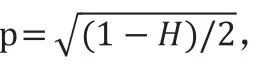
3 量子网络抽签系统
网络抽签系统的核心功能在于为参与抽签各方提供一个公平的抽签结果。一般而言,抽签适用于任何存在资源竞争的场景,例如,技能比武、房屋销售、资源分配等。当资源数量小于竞争者数量时,便可以满足抽签需求。在现实生活中,当竞争者都在场时,一次公平的抽签可以很容易被实现。但是,假如一个或者多个竞争者不在场时,此时,就需要通过网络抽签来解决。因此,评价一个网络抽签系统性能好坏最重要的方法是利用现场抽签的公平性来衡量。换而言之,使用某网络抽签系统完成一次抽签的效果要等同于一次现场抽签。一次公平的抽签必须满足以下条件:
(1)抽签结果的公平性;
(2)抽签结果的不可篡改性;
(3)任意一方不能完全控制抽签系统。
在一次真实的抽签应用场景中,抽签结果的使用方法会因应用需求不同而不同,但是,无论怎么改变抽签结果的使用方法,抽签规则都必须提示公示给每一位参与者得知,且征得所有人的同意。例如,在军事演习中,我们可以事先规定抽签结果按照奇偶性分为两类。而在出场顺序抽签中,我们可以事先规定出场顺序按照抽签结果从小到大依次排序。在本文中,我们将不考虑上述抽签结果应用环节,而只考虑抽签系统如何生成随机且公平的抽签结果。
抽签结果的公平性意味着抽签规则的合理性。假设存在某抽签可以按照自己全部或者部分的意愿控制抽签结果,则该抽签系统是不合理的。换而言之,对于一个公平的抽签系统而言,任意抽签方都不能通过作弊的方式完全控制最后的抽签结果。其次,抽签结果应当具有不可篡改的特性。为了进一步保证公平性,任何抽签方都不能对自己的抽签结果进行否认和抵赖。最后,任意一方不能完全取得控制权也是一个合理的抽签系统应当具备的特性之一。
3.1 抽签方案
为了实施网络抽签,必须先构建一个量子网络抽签系统的整体架构,图1 为本文提出的一种中心节点型的网络结构。中心节点作为仲裁方,可与其余任意节点共同运行一次或多次量子掷币协议,由量子掷币协议的安全性来保证掷币结果的公平性,掷币结果则为抽签结果。除中心节点外的其余节点则为参与抽签各方,即抽签方1,抽签方2,…,和抽签方n。

图1:量子抽签系统网络结构
图1 所示网络一般为量子通信网络,用于运行点对点量子掷币协议。由于实际的量子通信信道存在一定的量子噪声,如光子丢失和退相干,因此,本方案采用“ZZ2015”协议来产生抽签结果。具体而言,仲裁方分别与抽签各方运行多次“ZZ2015”协议,得到所有抽签方的抽签结果S,即S={s,s,…,s}。S 中任意元素s的取值为比特串,其中,比特串中的每一个比特位取值为运行一次“ZZ2015”协议产生的掷币结果。比特串的长度由抽签各方的总人数决定,例如,当n=8 时,比特串的长度为3,即仲裁方与任意抽签方i 运行3 次“ZZ2015”协议即可。
3.2 点对点量子掷币协议
实现本方案的关键在于采用合适的点对点量子掷币协议,使得每一个掷币结果是公平的,任意抽签方都不能完全控制掷币结果。虽然,量子掷币协议的安全性超过了经典掷币协议,但是,其致命的问题在于不能抵抗噪声,即其安全性在噪声信道中完全归零。因此,本方案采用“ZZ2015”协议来产生掷币结果。
一般而言,量子掷币协议在实际噪声信道中运行时,掷币双方Alice 和Bob 可以采用如下策略来控制协议:假设Alice 是不诚实方,当Bob 公布自己的经典比特后,Alice 随即根据自己的喜好值,公布一个假的编码信息。此时,若Alice 公布的制备基与Bob 的测量基一致,且信道中不存在丢失或者噪声的话,Bob 的测量结果应该等于Alice 公布的编码信息。但是,Alice 公布的编码信息是虚假的,会以一定概率使得其与Bob 的测量结果不一致。当此情景出现时,Alice 可以信道噪声为理由,逃过Bob 的检测。换而言之,Bob 在噪声信道中无法区分噪声和Alice 的作弊行为,Alice可以完全控制掷币结果,我们把这种情况定义为掷币盲区(简称BA)。
掷币盲区是导致大部分量子掷币协议在噪声信道中失效的根源,因此,“ZZ2015”协议引入了嵌套式结构,如图2 所示,从根本上消除了掷币盲区。当然,代价是牺牲一部分协议的效率。图中p(i=1,2,…,n)表示不能抵抗噪声的点对点量子掷币协议,当n 个不能抵抗的点对点量子掷币协议组成图示的嵌套式结构时,便可以消除BA,即达到了容噪的目的。具体而言,当运行p时,假设没有出现BA,则协议运行结束,产生可信的掷币结果0(1),反之,则继续运行协议p。从实用性考虑,本方案中的点对点量子掷币协议p应选取能够抵抗信道丢失的协议。协议的嵌套次数n也应该在运行之前约定好,因为n 越大,作弊的概率越高。

图2:嵌套式量子掷币协议结构
这样的嵌套式结构可以抵抗消除BA,从而抵抗噪声攻击。当掷币盲区出现时,假设其由真信道噪声引发的概率为p,则其由欺骗方引发的概率为1-p。因此,当BA 连续出现n 次时,噪声引发的概率则低至,而由欺骗方引发的概率高达1-p,此时,诚实方有充足的信心断定对方有欺骗行为发生。
当然,使用该协议时,必须考虑到误判情况的出现。当Bob 的测量结果与Alice 公布的信息不一致时,有可能是Alice 的欺骗行为导致,也有可能是真正的信道噪声导致,此时,若Bob 将信道噪声误判为Alice 的欺骗行为,他将立即终止协议,因而产生了误判。在实际应用中,必须平衡效率与安全性之间的关系。一般而言,嵌套的层级越多,即n的取值越大,则误判的可能性越小,因为连续n 次出现噪声的概率低至p,因此,当n 的取值增大时,Alice 的欺骗行为导致异常的可能性更大。同时,n 的取值越大,则Alice欺骗成功的概率也越大。因此,该协议实际上是牺牲了一部分协议的效率来换取安全性。
4 公平性分析
为了计算Alice 和Bob 各自最大的作弊成功概率,首先分析单次运行协议p,Alice 和Bob 各自的作弊成功概率。在无噪环境下,Alice 和Bob 最大作弊成功概率由以下不等式表示:

其中,T和T分别表示Alice 和Bob 所能采取的作弊策略,H和H分别表示Alice 和Bob 为诚实方。在噪声环境下,Alice 和Bob 最大作弊成功概率则由以下不等式表示:
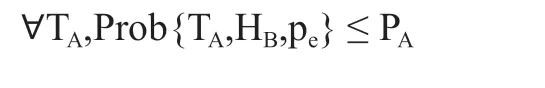
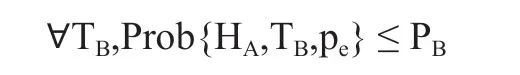
经过计算,可得Alice 和Bob 的最大作弊概率为:
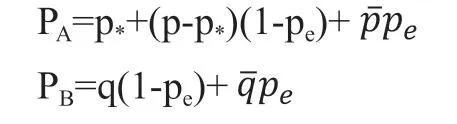
由此可见,Alice 和Bob 都可以利用噪声提高自己的作弊成功概率。
对于Alice 或者Bob 的作弊能力,一般假定其可以采取不违背量子力学的任何作弊策略。另外,对于信道噪声率p而言,一般只考虑p<0.5 的情况。因为当p>0.5 时,根据协议的对称性,Alice 或者Bob 可以采取相反的策略以达到p<0.5 时的作弊效果。Alice 和Bob 的最大作弊成功概率可由以下两个定理分别给出。
定理1:假设Alice 和Bob 运行嵌套式结构的迭代次数n=N,则Alice 的最大作弊成功概率为:
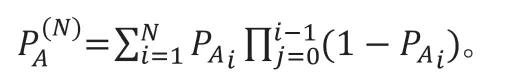
定理2:假设Alice 和Bob 运行嵌套式结构的迭代次数n=N,则Alice 的最大作弊成功概率为:
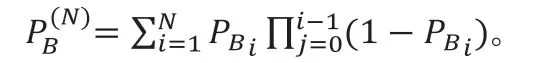
推论:Alice 和Bob 的最大作弊概率都小于1。?

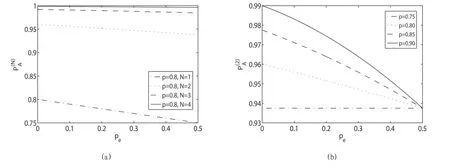
图3:Alice 和Bob 的最大作弊成功概率函数
图3(a)表明,Alice 的最大作弊成功概率函数是关于信道噪声p的递减函数,且随着迭代次数的增加,其作弊成功的概率会随之增加。因此,为了提高成功概率,Alice必须想尽办法降低信道噪声。由于之前假定Alice 和Bob 可以采用任何不违背量子力学的欺骗策略,因此,Alice 可以用一条无噪信道替换掉现有信道,使得p=0,此时,她的成功概率最高。同理,图3(b)表明Bob 的最大作弊成功概率函数也是关于信道噪声p的递减函数。Bob 亦可采用无噪信道替换的方式使得其作弊成功概率达到最大。
从表1 可以看出,即便Alice 和Bob 可以拥有不违背量子力学的一切能力,即他能替换掉任意一条量子信道,他也仍然不能完全控制协议。随着当迭代次数达到6 时,该协议的安全性已经变得非常低,即Alice 或者Bob 都几乎可以完全控制协议。因此,在实际应用中,必须严格控制迭代次数。
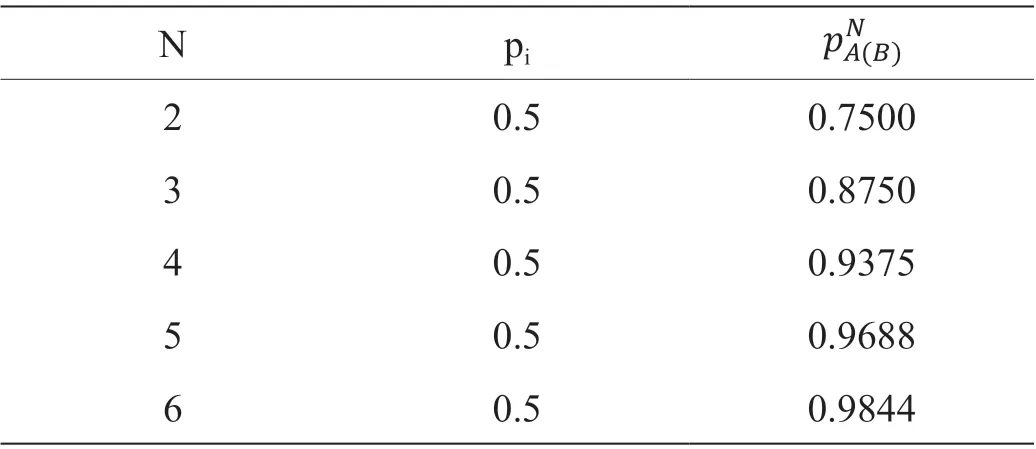
表1:协议在理想情况下的安全指标
由此可见,尽管该协议可以实现噪声容忍,但是,协议的安全性和效率是一对平衡指标。换而言之,误判率的提升可以提高协议的安全性,但是,协议的效率被牺牲了。当然,为了换取最高的安全性,协议的迭代次数n 可以被强制设定为1,此时,Alice 作弊成功的概率最低。但是,n 为1 时,协议的效率明细最低,即错误率达到最高。这种情况一般不会再实际应用中出现。
5 小结
本文提出了一个量子网络抽签方案,在该方案中,仲裁方与各抽签方分别运行量子掷币协议,产生一个多比特的掷币结果,该结果可作为抽签的依据。本方案采用嵌套式量子掷币协议,每一个嵌套元素可以采用现有任意一个信道丢失容忍的协议,通过这样设计,该量子网络抽签协议可以在实际噪声信道中运行,实现公平的掷币。结果表明,即使抽签方具有无穷多的计算资源,他(她)都无法完全控制最后的抽签结果。

