一种高隐蔽性跳频同步算法

肖文奎 张文学

（中国电子科技集团公司第七研究所 广东省广州市 510310）

当前战术通信系统可能受到的电磁干扰，已经从传统的能量型压制干扰转变为能量型和灵巧型干扰并存的状态。随着电磁环境的日益复杂，传统通信的稳定性受到了极大的挑战，跳频通信作为一种有效的抗干扰手段获得了诸多关注。为了提升通信的抗干扰和抗截获性能，需要更大的跳频范围和更快的跳频速度：更快的跳频速度能够让通信双方在被敌方捕获频率之前，就切换到新的载波频率，以降低截获概率；更大的跳频范围使得通信双方能够规避频带阻塞干扰机，在强干扰机存在的条件下维持通信。

跳频通信中最重要的一步是跳频同步，收发双方以伪随机跳变的频率的前提是建立在精确地时间同步。为了接收到完整的跳频信号，接收机必须首先与发射机实现跳频图案的同步，才能实现载波同步、码元同步等功能。针对跳频同步序列中相关码的快速盲识别，文献提出了结合伪随机序列统计特征和本原多项式识别同步跳，在此基础上可进一步实现对跳频信号的侦测和信息对抗。如果同步跳在短时间内使用的频率数量少、统计特征呈现周期出现特征，则干扰方更容易先推测出同步频率，然后进一步解出同步信息内容，实施后续干扰。

针对“由于跳频同步策略中用到的频点数量相对随机跳（业务跳）的频点数量少得多，而且由于其重复性很高，极易受到敌方的侦测和干扰，给系统的可靠性带来极大的隐患。通常的同步头法和自同步法的跳频同步策略，很难抵抗敌方的单音和多音干扰”的问题。文献提出一种对抗方法：敌方侦测到同步跳频点并施加干扰时，我方有少许时间是可以有效通信的，提出发端序列中任意两个频点所确定的位置信息是唯一的，固可以推断出当前收到的频点信息与同步跳转随机跳位置之间的距离，亦可以给出同步跳转随机跳的时间信息，这是所需要的，而且以同样频点组成的这样的序列有很多组，可以保证发端同步序列在频点确定的情况下，可以有较大的选择空间。

针对基于TOD 同步的跳频系统，文献提出一种跳频同步过程，具有跳频周期短、跳频点数少和周期循环规律强等特性。提出了一种跳频干扰方法，以识别、分离并干扰同步信号的方式来破坏跳频系统的正常工作，为进一步对跳频同步信号实施同步瞄准式干扰建立基础。

上述针对跳频同步的干扰及抗干扰研究情况表明，针对同步频点的干扰已经具有一定的可行性，亟需改善同步频点序列算法，加大短周期内同步频点集合数量，提高同步频率序列随机性。

1 基本原理--跳频同步过程

跳频通信系统信号发送和接收原理分别如图1 和图2 所示。

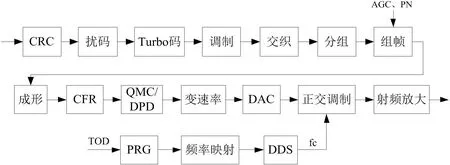
图1： 发射机的信号处理原理框图

图2： 接收机数据处理框图

在图1 和图2 中，都包含有伪随机序列发生器（Pseudorandom number Generator，下称PRG）和频率映射模块，这两个模块用于计算通信频率。为使系统具备更强的跳频抗干扰能力，需要PRG 能在跳频同步信息TOD 的控制下，产生均匀分布、特别长周期的伪随机序列（Pseudorandom number，下称PN），使其难以被敌方破解。

虽然需要通过将同步频率序列进行高度随机化和均匀化处理，但是，为了使通信双方建立同步的时间满足实际作战需要，还是要进行某些参数的约束。本文假定通信双方基于TOD 进行跳频通信的频率序列计算，主台与从台建立跳频同步所允许的最大时间差不大于8 分钟，即要求双方TOD的bit47 ～bit20 相差数值的绝对值≤1。在此基础上，进行同步频点序列的伪随机性和均匀性计算，保证从台在5 分钟时差范围内能实现与主台的跳频同步。

2 全频表高随机同步序列算法

2.1 全频表分布同步发送帧结构设计

跳频通信多以TDMA 方式组网，周期性设置同步时隙，主台在同步时隙发送TOD 信息，供从台向主台对准时序。以如图3 所示的帧结构为例，基本TDMA 周期为50ms，在下行时隙中设计了用于系统同步的物理同步信道时隙，跳频同步信号在此时隙发出。

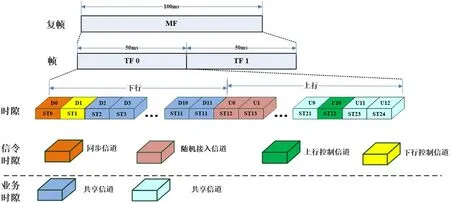
图3： 帧结构示意图

考虑全频表高随机同步频率算法需要，以频表容量64为依据，定义一个超帧周期（extra frame，缩写为XF），1 个XF 帧周期含16 个TDMA 帧周期，每个TDMA 帧含1个同步广播时隙，每时隙4 个同步跳，应把频表内的所有64 个频点用到1 个XF 周期内的64 个同步跳，达到短周期内同步跳的频点在全频表且均匀分布的目的。

2.2 高随机同步频率序列算法

高随机同步频率序列算法生成的频率序列，需要满足序列的随机性、频点出现概率的均匀性要求，构造PRG 如图4 所示，主要包括以下部分：

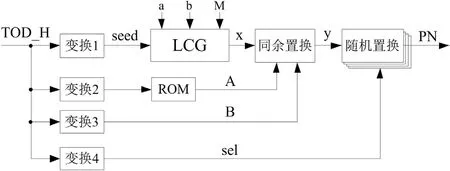
图4： 跳频序列发生器PRG

2.2.1 TOD_H 输入

表 示TOD 的 高 段，这 里 取TOD 的bit47 ～bit20，2000H/s 跳速时，约8.7 分钟变化一次，每变化一次则重新向下一级输出更新的参数。以TOD 作为PRG 模块的输入，使得通信系统对外呈现随机性，而对通信系统内部具备一定的确定性。

2.2.2 TOD 变换模块

图4 中的各TOD 变换模块，对TOD 进行一定格式转换，起到对所使用原始数据的加密功能。

2.2.3 LCG 模块

线性同余产生器（Linear Congruential Generator，下称LCG)用于产生均匀、随机数字序列x。然后设计一个很难用数学表达式进行统一描述的数据处理方法，对x 进行变换，成为跳频序列PN。

LCG 用下面的递归方法产生均匀分布的伪随机数据x，周期为2：

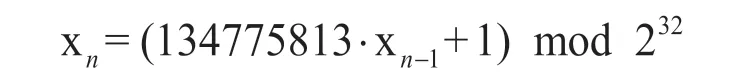
其中，x是预设的初始状态，即种子。主台可取每个XF 开始时TOD 高位的一段值，称为TOD_H，在后续的同步跳中通过一定的方法将TOD_L（TOD 低段的值）信息发给从台，同步后的从台将该TOD 信息更新本地TOD，与主台一致。

2.2.4 同余置换模块

同余置换模块先将x 转换为数值范围1 ～F（可用频点数）内的序列s；再做非线性的置换运算，使得难以根据y 反推出LCG 的表达式及状态：

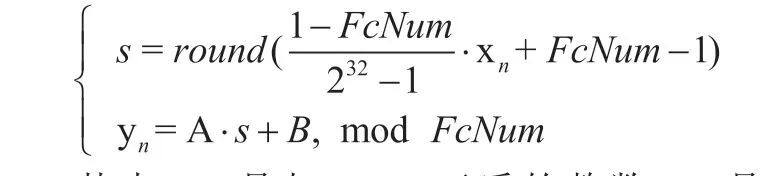
其中，A 是与F互质的整数，B 是0 ～F-1 的任意整数，保证y 构成一组分布在0 ～FcNum-1 之内的完全剩余系。备用的系数A 存储在ROM 中，见表1，由TOD数据经过变换以后选取其中一个，参数B 也是由TOD 数据生成的。每一种A、B 组合对应一种不同的数据映射方式，相当于一种加密方法。当F=64 个频点时，按表中的数据，有4096 种映射方式。

表1： 备用系数表

将x、y 轴上的数据分别取为s(2n)，s(2n+1)时的分布图称为2 维分布；x、y、z 轴上的数据分别取为s(3n)，s(3n+1)，s(3n+2)时的分布图称为3 维分布，性能较差的伪随机序列有可能会出现线状、平面状的有规律分布，易被破解，可采用置换方法，避免该问题。

2.2.5 随机置换模块

随机置换模块对同余置换后的一组输入y（F个数据），进行非线性变换，进一步隐藏PN 序列的规律，降低被破译的可能性。随机置换也是一一映射的，映射表的长度为F，用随机排序的方法产生。当F=64 时，共有种映射方案。在设备出厂或者执行任务之前，从中随机的选出64 种作为备选表，写入各电台内部。在运行时，由TOD 的时间字段产生控制信号sel，选用其中一个映射表用于数据置换。

两种置换方案结合起来以后，将在跳频序列中随机使用超过26 万种数据加密方法。这种序列的特点是，一方面，其规律无法用数学表达式来描述，难以破解；另一方面，复杂的数据置换方法并不改变序列的均匀性，使各频点是仍然接近等概率出现的。

PN 序列的周期：如果主台从不修改其种子，则：

周期≈2×同余表数目×随机置换表数目，约为2，相当于数万年。

图5 是从该PN 序列内任意截取的一段，F=64。可以粗略看出，在任意较短的时间范围内，频点都分布得比较均匀。

图5： 任意截取的一段PN 序列

在较长的时间范围内，其概率分布也是比较平坦的，如图6 所示。作为对比，参考Matlab 软件随机函数randi( )所产生的0 ～63 伪随机序列s 的均匀性，s = randi([0, 63], 1,10000)。理想情况下，64 个频点平均出现，则每个频点出现概率为0.015625，在频率序列中，各频点出现的均匀性方面，本文方案优于MATLAB 提供的随机函数，频表内各频点出现概率较为收敛。

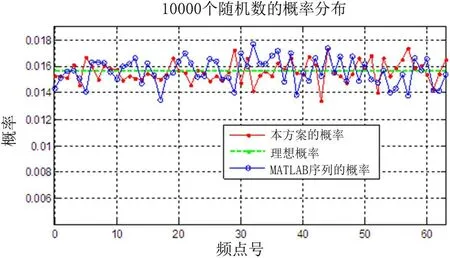
图6： 各频点的概率分布曲线

TOD 信息共48bit：32bit 的LCG 状态x+16bit 的时间信息。其中，时间信息T～T表示从以往某时刻到现在的时间差，只保留其最低的16bit。

TOD 数据决定了跳频序列的起始状态及加密规则，各参数的产生方法如下：

LCG 的种子seed：取TOD 的高32bit。

2.3 同步搜索过程

在一个XF 帧周期内插入64 个同步跳，按上面介绍的同步频点序列计算方法，则在一个XF 周期内，基本将频表中的所有频点都遍历了一次。

同步搜索时，从台从频表中依次取一个频点用于空口信号接收，每个频点最长持续接收一个XF 周期，在检测到同步信号时，从信号中解出主台发送的TOD 值（TOD 的bit19 ～bit0），临时替换为本地TOD 的低20 位，同时，为了确认收到的同步信息是否正确，需要启动对TOD 高位的验证。

以2000 跳/s 为例，允许从台与主台时差小于8 分钟情况下可以建立同步。在8 分钟时差范围内，可以保证收发双方TOD_H（bit47 ～bit21）的值相差不超过1，基于此，同步信息验证过程如下：

（1）第一步：本地TOD_H 不变，与接收到TOD_L（bit19 ～bit0）一起，输入PRG 模块，计算当前所处XF的同步跳接收频率。如果在本XF 周期内，可以在同步跳接收到同步信号，则将TOD_H 和TOD_L 作为本地新的TOD，进入后续正常接收。如果在本周期内，未能在后续同步跳收到同步信号，则转入下一步，尝试主台TOD_H 已进位的情况。

（2）第二步：本地TOD_H 进行+1 操作，与接收到TOD_L（bit19 ～bit0）一起，输入PRG 模块，计算当前所处XF 的同步跳接收频率。如果在本XF 周期内，可以在同步跳接收到同步信号，则将加1 后的TOD_H 和TOD_L 作为本地新的TOD，进入后续正常接收。如果在本周期内，未能在后续同步跳收到同步信号，则转入下一步，尝试本从台TOD_H 已进位的情况。

（3）第三步：本地TOD_H 进行-1 操作，与接收到TOD_L（bit19 ～bit0）一起，输入PRG 模块，计算当前所处XF 的同步跳接收频率。如果在本XF 周期内，可以在同步跳接收到同步信号，则将加1 后的TOD_H 和TOD_L 作为本地新的TOD，进入后续正常接收。如果在本周期内，未能在后续同步跳收到同步信号，则重新转入搜索。

2.4 同步频率序列周期

本文采用LCG 模块产生同步跳随机序列，其算法公式如下：

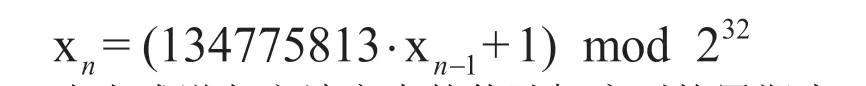
由上式递归方法产生的伪随机序列的周期为2，根据前面设计的同步跳超帧含64 个同步跳，则2跳÷64 跳/超帧×0.8s/超帧= 53687091s，约为621 天。也就是说，跳频同步频率序列621 天呈现一次周期性重复，这远远超出了系统连续时长，跳频同步的发送频率已经完全隐藏在全频表中。在常规的连续观察窗口内不具备任何显性规律，从而完全可以避免针对传统跳频中同步头的针对性攻击，有效提升了系统同步建立的成功率。

3 结论

传统跳频频率算法中，每跳都将TOD 的当前计数值进行变换，并作为新种子更新到随机序列发生器中，这在很大程度上破坏了伪随机序列的随机性。本文计算同步跳工作频率时，每个超帧只更新一次随机序列发生器的初始种子，保证了每个超帧内的所有同步跳频点分布的随机性和均匀性。再通过参数加载的方法，保证在高位TOD 计数值变化周期内各超帧同步频率计算种子的相异。这样使得在整个跳频过程中，同步跳使用频率都能保证较高的随机性和均匀性。本文提出的全频表高随机性同步头发送频率算法，实现了高隐蔽性跳频同步过程，可应用于基于TOD 的跳频通信系统装备中。