基于改进粒子群算法的工业润滑油调和方案设计

陈鑫悦

（中国人民解放军战略支援部队信息工程大学密码工程学院，河南 郑州 450000）

0 引言

随着工业化的发展，人们的生活已经离不开各种机械。而每种机械都需要工业润滑油对其进行防锈、润滑、缓冲的保护，这是机械运作中不可或缺的一部分。

润滑油是用两种或多种不同指标的基础油按照不用的比例进行混合产生的。润滑油的调和过程中理化性质会发生改变，它的性质变化与各基础油的指标可能是线性或非线性关系，所以工业润滑油的调和是一个复杂的工艺问题。衡量润滑油的性能指标主要包括黏度、凝点（倾点）、酸值、闪点、氧化安定性、残炭，等等，本文主要针对这6个指标（Y，Y，…，Y）进行调优方案的设计。

现有文献中大部分都从润滑油的黏度属性方面或者润滑油各属性之间的相互影响进行研究，一般只得到定性结果，很少见到定量具体分析，不利于对润滑油调和方案的制定与提高。为简化问题，本文忽略润滑油的生产技术和过程，且不考虑添加剂问题，仅仅从数学角度研究润滑油的调和优化问题。同时，假设润滑油的某一指标i只与基础油的相应指标i有关，i=1，2，…，6。针对不同的需求，本文建立了两种非线性约束目标优化数学模型，使用改进粒子群算法（Improved Particle Swarm Optimization,IPSO）进行求解。本文接下来的工作安排：首先介绍润滑油的配比模型以及两种调和方案的数学模型；其次介绍改进粒子群算法；再次进行实验测试；最后总结。

1 润滑油调和的数学模型

1.1 配比模型

10种基础油的配量分别为x，x，…，x，10种基础油有6个性能指标分别定义为a，…，a，润滑油的六项性能指标为Y，Y，…，Y。从混合浓度公式角度出发，如式（1）所示，认为不同基础油的配比与润滑油的各指标分别存在一个关系式。

针对式（1），笔者对其中每个变量添加相应参数β，变为式（2）。

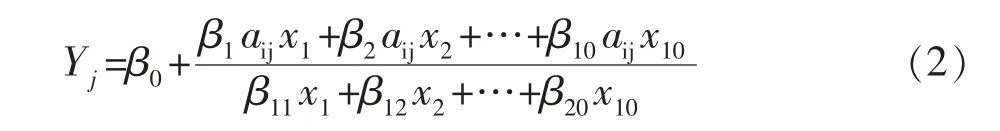
然后通过20批次生产数据，使用最小二乘法对式（2）进行非线性曲线拟合，求解参数。最终结果如表1所示。其中最大的均方误差为0.3×10，说明拟合效果优秀。

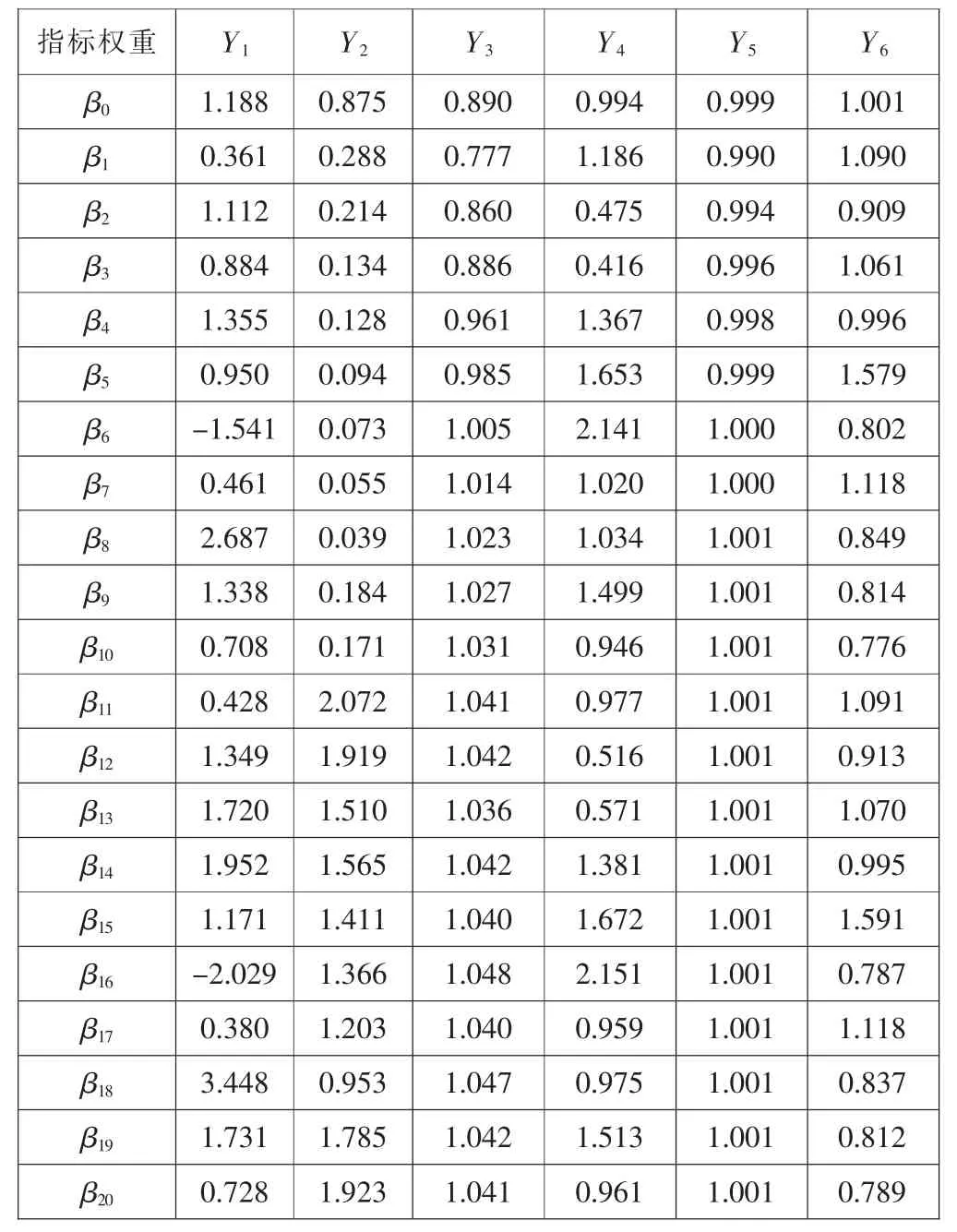
表1 配比模型权重系数

1.2 非线性约束目标优化模型

质量需求：在不考虑成本的情况下要求最大限度地符合润滑油的指标要求，各指标的相对误差最大不超过5%。通过各指标拟合值f与指标要求值y的相对误差以及惩罚函数来构建目标规划模型，如式（3，4）。

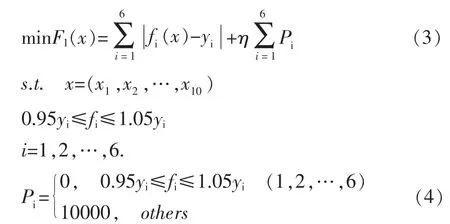
式中，P为惩罚函数，用于控制约束条件；η为调节系数。

成本需求：在要求成本最低的情况下，满足各指标的相对误差最大不超过5%。构建成本需求数学模型如式（5）所示。

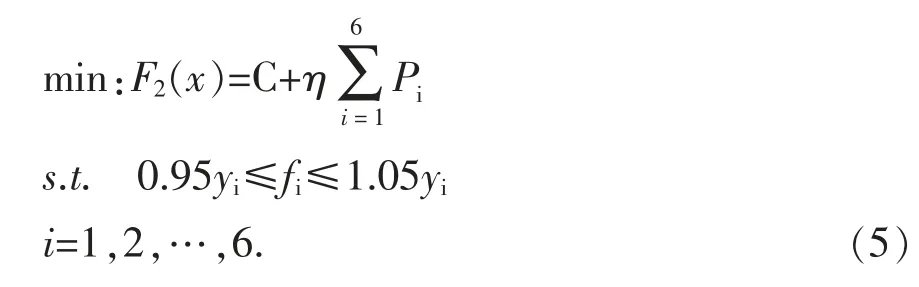
其中总成本C的公式如式（6）所示。

式中，c为基础油i的价格。

2 改进粒子群算法

粒子群算法，又称粒子群优化算法（Partical Swarm Optimization），由Eberhart博士和Kennedy博士于1995年提出，属于群智能算法的一种。它源于对鸟群捕食行为的研究。假设区域里就只有一块食物（即通常优化问题中所讲的最优解），鸟群的任务是找到这个食物源。鸟群在整个搜寻的过程中，通过相互传递各自的信息，让其他的鸟知道自己的位置。通过这样的协作，来判断自己找到的是不是最优解，同时也将最优解的信息传递给整个鸟群。最终，整个鸟群都能聚集在食物源周围，即上文所说的找到了最优解，也就是问题收敛。

针对粒子群算法容易陷入局部最优解的缺点，本文改进惯性权重的更新方式，使用随机的惯性权重函数，如式（7）所示。

式中，w和w分别为最大和最小的惯性权重值；rand为[0，1]上的均匀分布。这样就使得粒子种群代与代之间以及同代之间的不同个体都具有一定的随机性，增强了粒子多样性，一定程度上缓解了粒子群算法易陷入局部最优解的缺点。

IPSO算法流程图如图1所示。

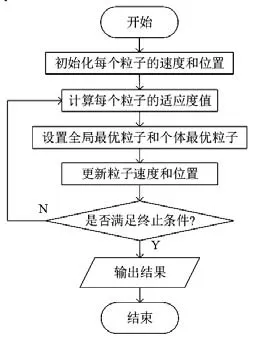
图1 IPSO算法流程图

3 实验测试

本节将对两种不同需求设计的数学模型进行测试，使用的十种基础油的价格如表2所示。调和的润滑油需要满足的指标如表3所示，总共需要70 000吨。本文的实验均在笔记本电脑上运行，CPU是i5-4200M，内存8G，显卡GT820。所有算法在MATLAB2019a平台实现。粒子群算法和改进粒子群算法的种群数为50，迭代30次。

表2 基础油价格表

表3 润滑油性能指标要求

3.1 质量需求数学模型测试

首先将本文提出的IPSO与PSO的寻优过程进行对比，从图2中可以看出IPSO具有较快的收敛速度和寻优能力。

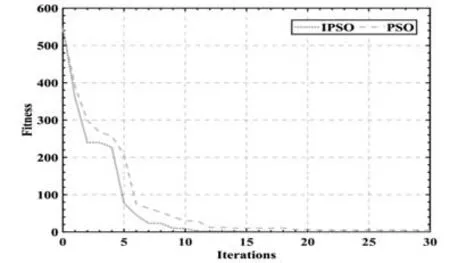
图2 IPSO与PSO迭代变化图

得到的各基础油用量如表4所示。从表5中可以看出，得到的优化方案润滑油性能指标与要求值的最大误差为1.2%。各指标误差很小，但是总的成本达到了218 744 814元。

表4 质量需求优化方案的基础油用量

表5 质量需求优化方案的润滑油性能指标

3.2 成本需求数学模型测试

同样的使用IPSO算法对成本需求数学模型进行求解，表6中显示的数据是需求二优化方案的基础油用量及比例，优化后计算出总成本为191 910 000元，2 741.6元/吨，远远小于需求一中的总成本218 744 814元，大大减少了成本。同时，只追求成本最小，导致最大的指标误差为4.98%，如表7所示。

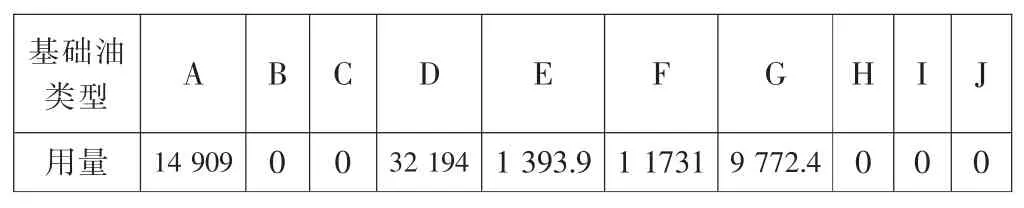
表6 成本需求优化方案的基础油用量

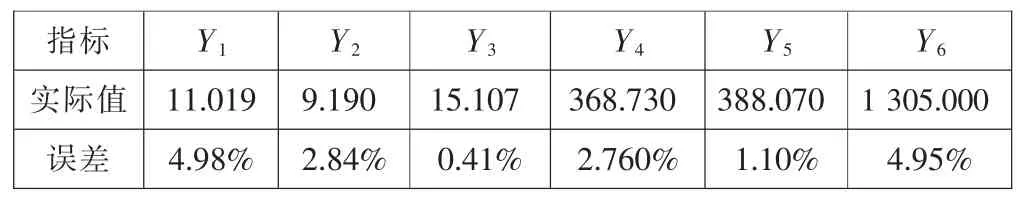
表7 成本需求优化方案的润滑油性能指标

4 结语

针对工业润滑油调和的复杂问题，本文提出了两种非线性约束目标优化数学模型。为了能够迅速、准确地寻找最优的调和方案，本文提出了改进粒子群算法，使用随机惯性权重，增加每个粒子的多样性，从而降低进入局部最优解的概率。另外，本文设计了两组实验，对本文提出的数学模型和算法进行测试。第一组实验的优化方案得到的润滑油指标最大误差仅为1.2%，符合质量设计需求。第二组实验的优化方案得到的润滑油成本总成本为191 910 000元，远远小于需求一中的总成本218 744 814元，大大减少了成本，符合成本设计需求。因此，本文提出的方法对于工业润滑油调和方案设计具有一定的参考价值。未来的工作中，可考虑将影响润滑油调和的更多因素（如温度、添加剂等）添加到优化方案中。