基于网络教学平台和Mathemat ica的高等数学实验教学模式研究

李 敏

（怀化学院数学与计算科学学院，湖南 怀化 418008）

0 引言

高等数学是理工经管类各专业的一门核心公共基础课程，对学生学习后续专业课程和培养学生数学思维能力都起着非常重要的作用。高等数学课程的教学目标在于让学生掌握微积分的基本理论和基本方法，培养学生抽象的思维能力、逻辑推理能力、实践应用能力和科研创新能力。

高等数学课程教学内容抽象、理论性强、计算复杂，对于数学基础不牢固的大学一年级本科生而言具有较大的学习难度。传统授课模式下，教师在课堂上往往过于重视理论的讲授、公式的推导和复杂计算过程的演示，忽视了对数学知识和方法产生的背景和数学技术的实践应用的介绍。因而导致学生难以理解所授内容的数学内涵和应用技巧，课堂教学对学生综合实践能力和创新能力培养不突出，课程教学难以支撑专业人才培养目标。传统课堂教学内容、教学模式和教学方法手段有待改革。

本文介绍笔者在近几年的教学实践中构建的基于网络教学平台和数学软件Mathematica构建的高等数学课程实验教学模式，新的教学模式落实了以学生为中心、以能力培养为核心、以问题为主线的现代教学理念。本文将从构建高等数学实验教学模式的理论和技术基础、教学组织方式、教学案例展示等方面展开。

1 基于网络教学平台和Mathematica软件的高等数学实验教学模式

1.1 高等数学实验教学的理论基础和技术支持

自2018年起，教育部高等教育司不断推进以学生为中心的高等教育改革，提出要在教学中突出“学生中心、持续改进、成果导向”的基本原则，为我国全面提高本科教育质量指明了方向。落实以学生为中心的教学理念，即要在教学活动中突出学生的主体地位，学生在自主发现、自主探索新知识及其意义的过程中进行自我构建。在高等数学课程中开设实验项目，让学生从问题出发，基于数学软件平台体验解决问题的过程，在实验过程中学习、探索和发现数学规律，是顺认新时代高等教育发展的举措。通过完成实验项目内容，学生在主动学习数学知识与技能的过程中提升综合实践能力，培养科学精神和创新意识。

笔者在近几年的高等数学实验教学的实践中选择Mathematica软件作为实验平台。Mathematica由美国Wolfram Research公司开发，它具有强大的数值计算功能、符号计算功能、图形程序设计功能和动态演示功能。笔者基于数学软件Mathematica自主设计了一系列集科学性、趣味性、应用性、启发性于一体的高等数学实验项目，这些实验项目是高等数学教学内容体系的重要补充。

1.2 高等数学实验教学方法和教学模式

在高等数学实验教学过程中，广泛应用任务驱动法和小组讨论法组织教学。任务驱动法是一种以学生为中心，以完成任务为驱动的教学方式，通过学生自主完成目标任务和解决问题来达成教学目标。教师是教学活动的主导者，在高等数学实验教学设计时，一般将实验项目教学内容分解成多个具体的任务，每个任务中都蕴含了相应的知识、能力和情感目标。学生基于实验指导书和Mathematica软件，通过小组合作和自主探索，不断发现问题、分析问题、解决问题，在完成任务的过程中发现新问题、探索新问题。在整个教学实施过程中，教师起到引导、帮助和组织协调的作用，学生真正成为教学活动的主体。

笔者所设计的实验项目均与高等数学课程中重要的知识点相关联，实验教学与理论教学相辅相成。为提高教学效率，授课教师在课前将实验指导书、实验程序、实验报告和Mathematica软件教程发布在超星网络教学平台上。学生基于教师发布的实验指导书、教学微视频、实验程序等在线学习资源自主探索，学生以小组合作的方式完成实验任务，教师根据学生在实验过程中提出的问题和实验报告完成情况进行适时指导，并通过组内自评、小组互评、集中讲评完成成绩评定。笔者基于网络教学平台和Mathematica软件构建了线上线下结合、课内课外互补、理论教学与实践探索并重的开放式、立体式高等数学课堂。所设计的实验项目均以问题为主线，学生在分析问题、解决问题的过程中学习数学知识与技能，在实验操作过程中培养数学技术实践应用能力，在发现和探究新问题的过程中提升科研创新能力。

2 教学案例介绍

函数是事物的内部联系在数量方面的反映，根据问题提供的信息建立描述函数及其导数关系的微分方程，进而可以求出函数的表达式。为介绍高等数学课程中齐次微分方程在解决实践问题中的应用，引导学生探索齐次微分方程的解法和微分方程的数值算法，培养学生的数学应用能力和科研创新能力，我们基于鸭子过河问题设计了一个实验项目.本节，我们以该实验项目为教学案例介绍高等数学实验教学组织模式和Mathematica软件在实验教学中的应用。

问题：设有两岸平行、河面宽度为h的小河，河水流速为a。有一只鸭子从河堤的A点游向正对岸的O点，设鸭子始终朝点O游，且保持恒定的静水速b（b>a），试运行模拟鸭子过河过程的计算机程序，观察动态模拟过程，建立描述鸭子游动轨迹的微分方程并探索其求解方法。

设置a=0.7，b=1，h=50，编写了模拟鸭子过河动态过程的Mathematica程序，代码如下：

运行程序即可生成模拟鸭子游动的动态演示界面，如图1（a）所示，学生基于演示动画对鸭子过河的过程有了非常清晰、非常直观的认识，同时模拟鸭子过河过程的程序设计方法为学生探索鸭子过河轨迹方程的解法提供了重要支撑。为建立描述鸭子过河轨迹的微分方程，在图1（b）所示的直角坐标系中分析鸭子的速度向量。设t时刻鸭子位于P（x，y），引导学生逐步分析鸭子游动速度表示方法。

图1 鸭子过河问题辅助图

在实验项目中，应用Mathematica的图形程序设计功能，对比方程的解析解与仿真模拟所得鸭子过河轨迹，帮助学生掌握应用数学软件和微分方程分析和解决实践问题的基本方法。为拓展学生的知识面，培养学生的科研创新能力，进一步引导学生探索微分方程的数值解法。设点列{P（x，y）}在方程解x=x（y）确定的曲线上，设y=y+d，由方程几何意义，学生可以直观地看到图1（e）中的割线和切线有相近的斜率，因此：

令y=h，x=0，如果d足够小，基于前面的微分方程，可以合理地构造迭代公式：

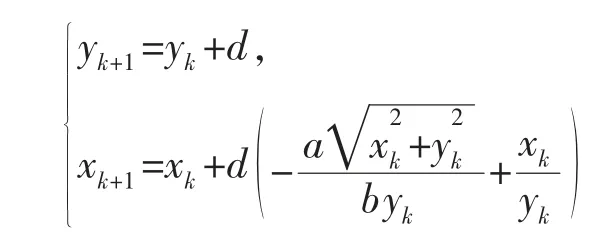
这就是求解本实验项目中的微分方程数值解的欧拉公式。设置a=0.7，b=1，h=50，d=1.0，应用该公式编程可得点列{P（x，y）}，图1（f）对比了数值算法产生的点列与解析解描述的曲线的一致性，同时也检验了算法的有效性。

学生通过完成上文介绍的鸭子渡河实验项目，学习了应用数学软件模拟平面上质点运动过程的基本方法，掌握了应用微分方程求解实践问题的方法和步骤，巩固了齐次微分方程的理论解法，同时探究了求微分方程数值解的欧拉法的基本原理，该实验项目能有效培养学生的实践应用能力、编程能力、科研创新能力。类似的教学案例和实验项目还有很多，限于论文篇幅，在此不一一列举。

3 结语

本文介绍了笔者在近几年的教学实践中构建的基于网络教学平台和Mathematica软件的高等数学实验教学模式。在高等数学实验教学实施过程中，学生对实验教学内容和数学软件都产生了浓厚兴趣，学生学习参与度较传统课堂大幅提高。基于笔者团队自主开发的高等数学实验教学资源，学生通过在Mathemaitca软件上自主完成实验项目，亲自动手完成实验内容，增进了对相关数学知识和方法产生的背景及应用领域的了解，有效提升了学生分析问题、解决问题、发现问题的能力，学生在探索完成一些具有较大挑战度的实验项目的过程中，很好地培养了其科研创新能力。