河口地貌对潮汐不对称性影响的数值模拟研究
周曾 ,陈璐莹,蒋春海,储鏖,Ian Townend,张长宽
(1.河海大学 水文水资源与水利工程科学国家重点实验室,江苏 南京 210098;2.河海大学 江苏省海岸海洋资源开发与环境安全重点试验室,江苏 南京 210098;3.上海勘测设计研究院有限公司,上海 200335;4.南安普顿大学 海洋与地球科学学院,南安普顿 SO17 1BJ)
1 引言
潮波从外海向河口内传播的过程中,由于受到地貌形态[1-2]、径流[3]、海平面上升[4]、人类活动[5]等影响产生变形,导致涨落潮不对称,这一现象通常被称为潮汐不对称性[6],也有学者进一步将涨落潮流速不相等的现象称为潮流不对称性[7-8]。在现有的研究中,大都对潮汐进行了简化,在保证动力场与实际情况一致或相似的情况下用若干起主要作用的特征潮来表达潮汐动力[9-10]。Friedrichs 和Aubrey[11]指出在世界上大部分的半日潮海域,起主要控制作用的是M2分潮和由M2分潮自身演变出的M4分潮,针对这一部分海域可以近似用M2分潮和M4分潮来描述水位和流速(公式(1)、公式(2))。并基于此提出了用M4分潮与M2分潮的振幅比ηM4/ηM2或uM4/uM2来判断潮汐不对称性的强弱,振幅比越大,潮汐不对称性越强;用M2分潮与M4分潮的相位差来判断潮汐不对称性的类型[11](表1),这一方法至今仍广为使用[12-13]。本文将从水位相位差、断面流速及余流分布等多角度入手来研究河口地貌形态对潮汐不对称性的影响。

表1 潮汐不对称性类型Table 1 The type of tidal asymmetry
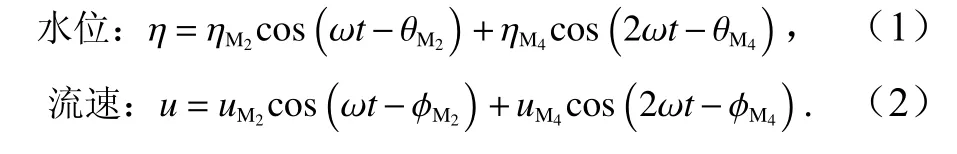
近年来,随着经济发展和河口海岸防护需求的提高,我国在河口区开展了建港、围垦等海岸工程[14],导致河口地貌形态发生了改变,从而影响了河口区的潮汐不对称性[15],由于水动力与地貌形态的互馈作用,又将进一步影响到河口地貌平衡形态[16]。例如,胶州湾的围垦工程改变了地貌形态,使其潮汐不对称性增强[17];象山港的围垦使得湾内潮汐不对称性发生改变,湾中部和湾顶由落潮占优转变为涨潮占优[18];珠江三角洲黄茅海河口的滩槽潮汐不对称性不同,潮滩为涨潮主导型,主槽为落潮主导型[19],长江口北支为涨潮主导型,但由于长江口北支断面从下游到上游不断缩窄,潮波变形加剧,使上游的潮汐不对称性更强[13];杭州湾-钱塘江口的岸线改变使得该区域的潮汐不对称性发生改变,部分区域涨潮优势增强,而部分区域的涨潮优势减弱[20]。以上这些现象表明河口地貌对潮汐不对称性的产生和发展有着重要影响。然而,潮汐不对称性的变化会直接影响河口地区的泥沙净输运,从而进一步对河口地貌进行重新塑造[21],研究潮汐不对称性可以对后续海岸工程的选址、建设以及维护进行指导[22],同时潮汐不对称性与径流的互相作用对河口地区的水质也有一定影响[23],因此研究河口地貌对潮汐不对称性的影响具有重要的现实意义和应用前景,亟需深入研究。
通过观测数据分析和数值模拟研究,发现当河口较浅且潮滩容积较小时,河口倾向于涨潮主导型,泥沙向陆发生净输运[24];当河口较深而潮滩较大时则倾向于落潮主导型[25-26],当潮滩的位置处于平均水位或略高于平均水位时,落潮流达到最强,落潮流随着相对潮振幅的增大而减小,当潮滩位于平均水位以下时,潮汐不对称性主要由相对潮振幅(即潮振幅与水深比值a/h)决定[27]。此外,河口主槽的断面形态、平面形态和长度对潮流也有较大的影响,研究发现上凸型的潮滩断面对落潮流的增强效果更为显著[28-29],从海向陆剧烈收缩的河口平面形态促进涨潮主导[30],这是因为随着河口收缩率的增加,潮波变形加剧,流速和波长增加[30-31]。最后,河口长度的影响主要体现在对于较短的河口,潮滩越大越倾向于落潮主导,而当河口长度较长时,较宽的潮滩则倾向于涨潮主导[32]。
纳潮量是反映河口内部水体和外海水体交换的一个重要参数,对河口泥沙冲淤有着重要影响。目前,关于河口地貌形态对潮汐不对称性影响的研究较少考虑纳潮量这一关键因子,然而河口形态的改变会导致河口的纳潮量产生变化,进而对潮汐不对称性产生巨大影响,打破河口水动力条件与地貌形态间的匹配关系。鉴于此,本文将基于英国Humber 河口数据,通过数值模拟进一步讨论在纳潮量相同时,潮滩或主槽断面形态的改变对河口潮汐不对称性的影响,也进一步探究河口长度以及收缩率的变化对河口整体以及潮滩、主槽上的潮汐不对称性的影响。Humber 河口是英国第二大河口,也是英国东海岸最大的河口,是英国最发达的区域之一。其拥有丰富多样的物种和栖息地,是欧洲最重要的鸟类越冬河口之一,同时也是一个重要的工业区和贸易门户,英国近1/4 的海上贸易都要经过该河口。由于其重要的社会、经济地位,成为世界上研究最多的河口之一,积累了大量的研究资料,因此本研究将其作为概化模型的参照河口。
2 模型建立及参数设置
本文利用Delft3D 软件中的水动力模块,基于英国Humber 河口数据和Townend 等提出的理想河口表达式[33-36]建立二维理论模型(图1),Humber 河口长约140 km,自西向东延伸,平均水深16.5 m,在大潮期间平均潮差达5.7 m。由于理论模型断面形态较复杂,因此在保证潮滩容积、主槽容积、底坡及平面形态不变的情况下将理论模型断面形态简化为潮滩断面呈线性变化,主槽断面为矩形。该简化断面形态常被用于河口地貌形态的研究,能较好地反映河口的水动力变化[32,37],且经验证后该方案模型与理论模型的潮汐不对称性与流场基本一致。基于该简化模型,根据常用的纳潮量计算公式[38-40],在保证纳潮量相同的情况下,将两种宽度(宽、窄)的潮滩和3 种主槽深度(较深主槽、基准深度、较浅主槽)进行组合,得到6 种不同断面形态的河口模型(图2,表2)。
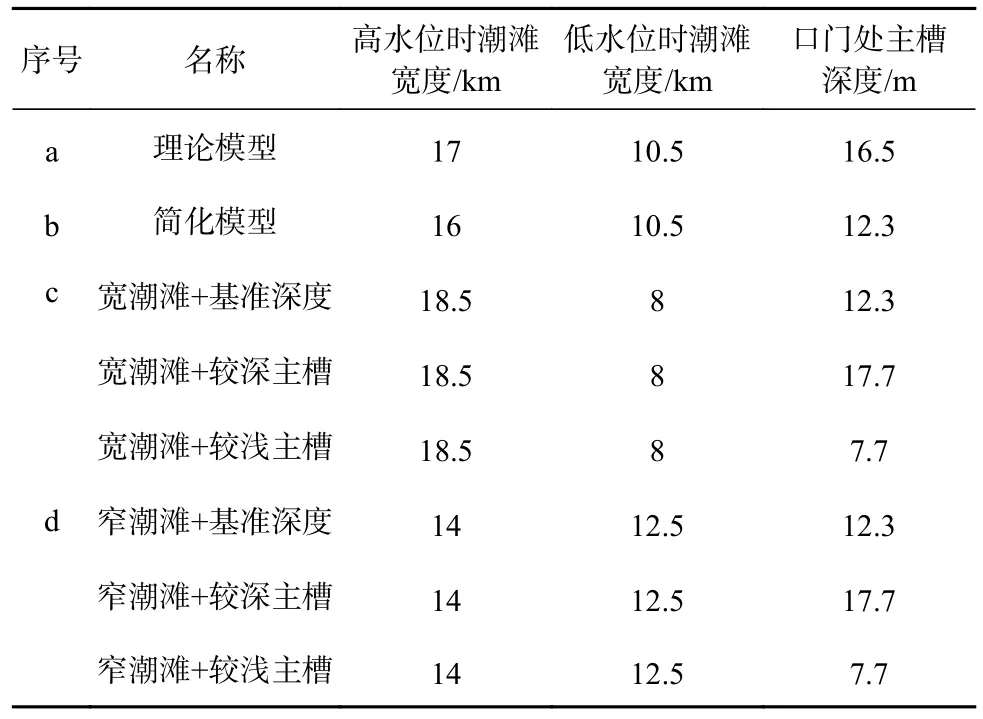
表2 不同断面形态模型汇总Table 2 The summary of different cross sections
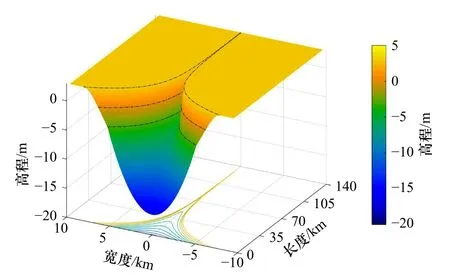
图1 基于Humber 河口数据的理论模型示意图[41]Fig.1 Schematic diagram of the theoretical model based on the data of Humber Estuary[41]
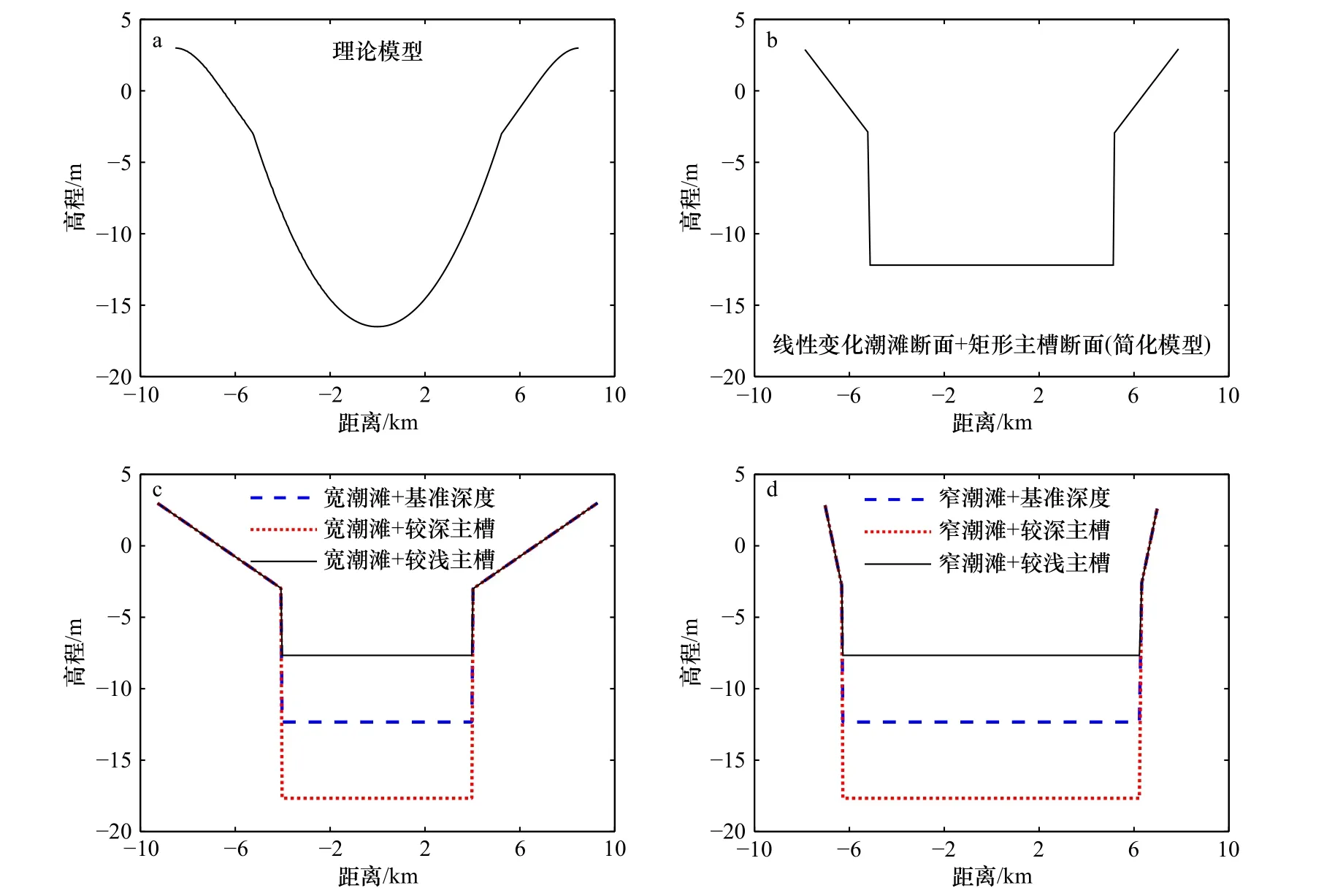
图2 不同断面形态示意图Fig.2 Schematic diagram of different cross sections
纳潮量(W)计算公式为
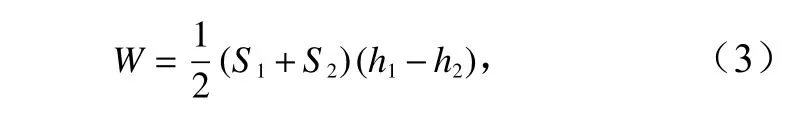
式中,S1、S2分别为高、低潮位时的水域面积(单位:m2);h1、h2分别为高、低潮位时的水深(单位:m)。
由于简化模型平面形态呈指数型收缩,河床高程沿程随河口宽度的变化而变化,因此在研究不同平面形态对潮汐不对称性的影响时,首先将简化模型的变化底坡改成平底。在其他参数不变的情况下,底坡为平底的简化模型只需要80 km 长即可达到变化底坡简化模型的纳潮量。基于该模型,在纳潮量不变的情况下,设置另外两种不同平面形态的模型(平面形态为矩形,平面形态线性变化)。同时,还另外设置了一个不同收缩率的指数型收缩平面模型来研究收缩率对潮汐不对称性的影响(表3)。通过设置模型外海侧的潮流过程,利用上游河道的径流过程进行驱动,其余均设为固边界。外海开边界现仅考虑M2分潮(太阴主要半日分潮),振幅为3 m(参照Humber 河口口门最大潮振幅),频率为28.985 5°/h,相位差为0°,上游河道径流设定为200 m3/s 的恒定流。模型模拟时间均为1 个月。

表3 不同平面形态模型汇总Table 3 The summary of different plan forms
3 断面形态的改变对潮汐不对称性的影响
通过分析断面平均流速随时间的变化(图3),可以看出涨潮最大流速大于落潮最大流速,宽、窄潮滩的最大涨潮流速均值分别为1.16 m/s 和1.34 m/s,而最大落潮流速分别为0.98 m/s 和1.04 m/s。潮滩宽度相同时,不同主槽深度下涨潮最大流速相差不大,宽潮滩对应的3 种主槽深度最大流速均约为1.15 m/s,窄潮滩对应的3 种主槽深度最大流速约为1.35 m/s。但对落潮流速而言,主槽越浅,落潮流速越小,落潮历时更长,印证了主槽越浅,河口更倾向于涨潮主导型。当主槽深度相同时,涨落潮的最大流速均是窄潮滩大于宽潮滩,窄潮滩最大流速约是宽潮滩最大流速的1.13 倍。

图3 不同潮滩宽度以及不同主槽深度的河口断面平均流速随时间的变化过程Fig.3 The change of cross-sectionally averaged along-channel velocities in estuaries with different tidal width and channel depth
由于断面平均流速不能展现出流速在潮滩以及主槽上的不同,因此取高水位、平均水位和低水位3 个时刻,对断面流速进行分析(图4)。首先,不管水位如何变化以及潮滩的宽窄,主槽越浅,断面面积越小,使得潮滩和主槽上的流速越大。为了保证纳潮量相同,缩窄潮滩的同时增加了低水位时的河口宽度,使得在相同水深的情况下,窄潮滩所对应的主槽面积大于宽潮滩对应的主槽面积,使得窄潮滩的断面流速小于宽潮滩的断面流速,例如在主槽较深深度情况下,宽潮滩在高水位(HWL)、平均水位(MWL)、低水位(LWL)的流速分别为 0.87 m/s、1.13 m/s、0.17 m/s,而窄潮滩在3 种水位状态下,流速分别为0.53 m/s、0.74m/s、0.05 m/s。
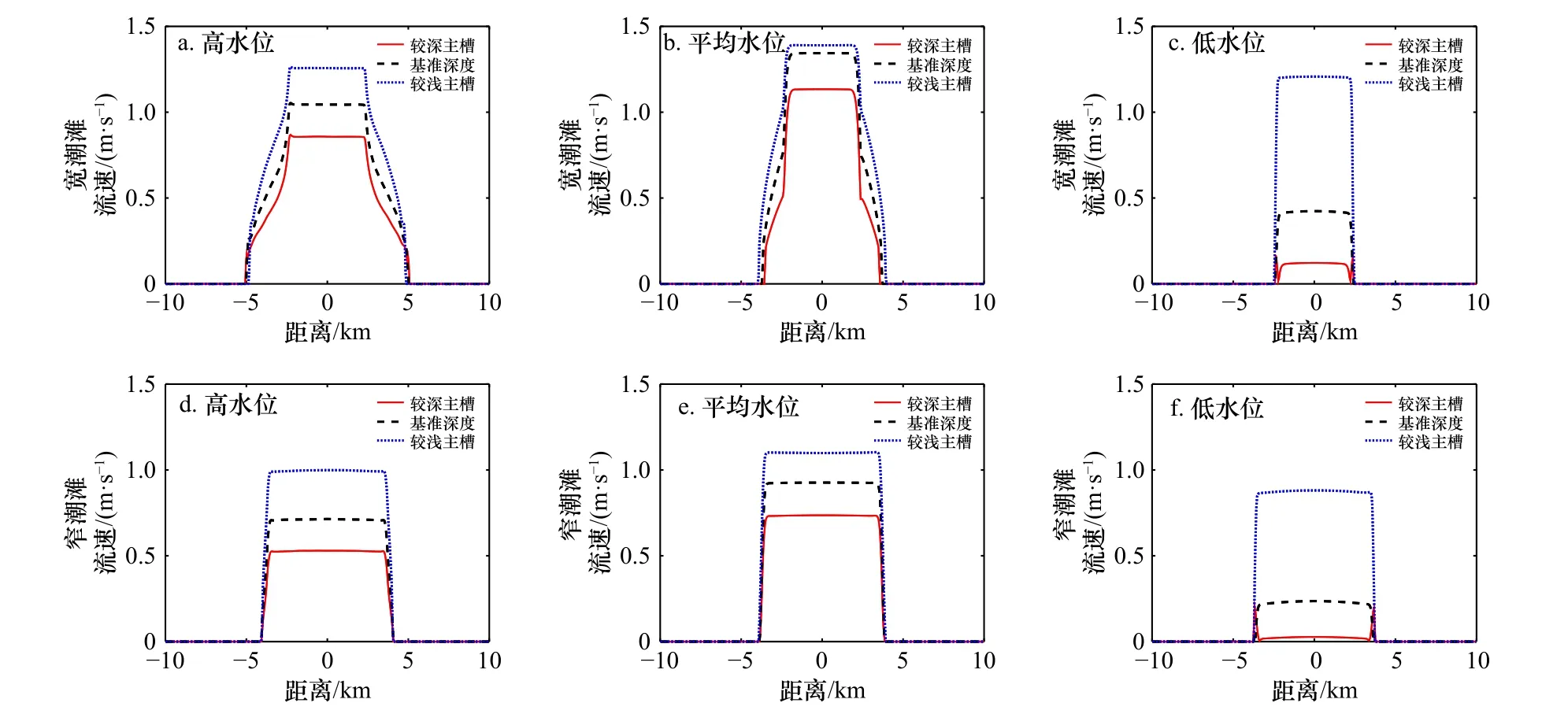
图4 不同潮滩宽度以及不同主槽深度的河口在不同水位下的断面流速Fig.4 Cross-sectional distribution of the along-channel depth averaged velocities in estuaries with different tidal width and channel depth under different tidal levels
分别取不同断面形态河口7 个潮周期内的水位变化过程进行调和分析并对所得的相位差沿程变化进行汇总(图5)。经计算,在河口的前60 km 范围内,相位差由口门处的-3°~3°迅速上升到约50°,60~140 km 范围内的相位差趋向于稳定,可以看出在纳潮量相同的情况下,不同的潮滩宽度和主槽深度会对沿程的潮汐不对称性产生影响,相位差的增长幅度最小为宽潮滩+较深主槽的54.31°到窄潮滩+较深主槽的61.2°,增加了12.7%,达到稳定状态的速度也不同,但总体的潮汐不对称性仍处于涨潮主导型,且沿程相位差均值相差不大。
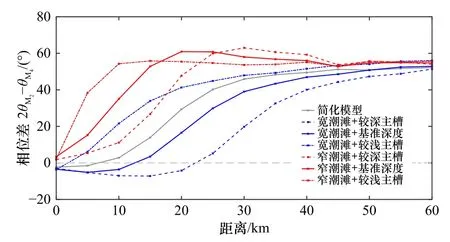
图5 不同断面形态的河口沿程相位差变化Fig.5 Changes of relative tidal phase along the channel in estuaries with different cross sections
对于较宽的潮滩而言(图5 中不同线型的蓝线,对应表4 中的b-d 3 种类型),平均延程相位差从主槽较深深度的45.51°上升到主槽较浅深度的56.10°,主槽越浅,相位差越大,越倾向于涨潮主导型,且相位差越快达到稳定状态。当潮滩较宽且主槽较浅时,相位差呈现从靠近口门处的-2°左右出现先略微减小2°~5°再增大的趋势,且其达到稳定状态所需的距离最长。这是由于宽潮滩会使河口倾向于落潮主导型,浅主槽使河口倾向于涨潮主导型,在口门附近潮滩较宽,而随着潮波向内推进,河口逐渐缩窄,潮滩变窄,主槽进一步变浅,使得河口的涨潮流逐渐增强,落潮流减弱。
对于较窄的潮滩(图5 中不同线型的红线,对应表4 中的e-g 3 种类型),无论主槽的深度如何,沿程相位差都会呈现先快速增长,到达峰值相位差50°~60°后开始减小,最后稳定在50°左右的态势,且主槽越深,峰值越大,到达峰值所需的距离越长。这说明较浅的主槽深度能使涨潮流快速达到峰值。而对于相同的主槽深度(图5 中以相同线型表示),总体而言窄潮滩更倾向于涨潮主导型,但是潮滩的影响因主槽深度的不同而不同,主槽深度较深时,潮滩的缩窄会使沿程相位差均值增加更多,也就是说潮滩大小对潮汐不对称性的影响在主槽较深的情况下更为显著。虽然口门处的断面形态差异较大,但随着平面形态以及底坡的变化趋势减缓,当距口门50 km 及更远后,不同断面之间的差异较小,主槽深度差异约为0.5 m,潮滩宽度的差异则在50 m 左右,因此潮汐不对称性逐渐趋于稳定且不同断面之间的潮汐不对称性差异不大。此外,从不同河口断面的沿程相位差均值(表4)来看,符合宽潮滩削弱涨潮主导,浅主槽增强涨潮主导这一理论。当主槽较浅且潮滩较窄时河口整体的涨潮主导最强,当主槽较深且潮滩较宽时河口整体的涨潮主导最弱。当潮滩较宽时相位差对主槽深度变化的响应相较于潮滩较浅时更为灵敏,主槽从深到浅时相位差增加得更多。
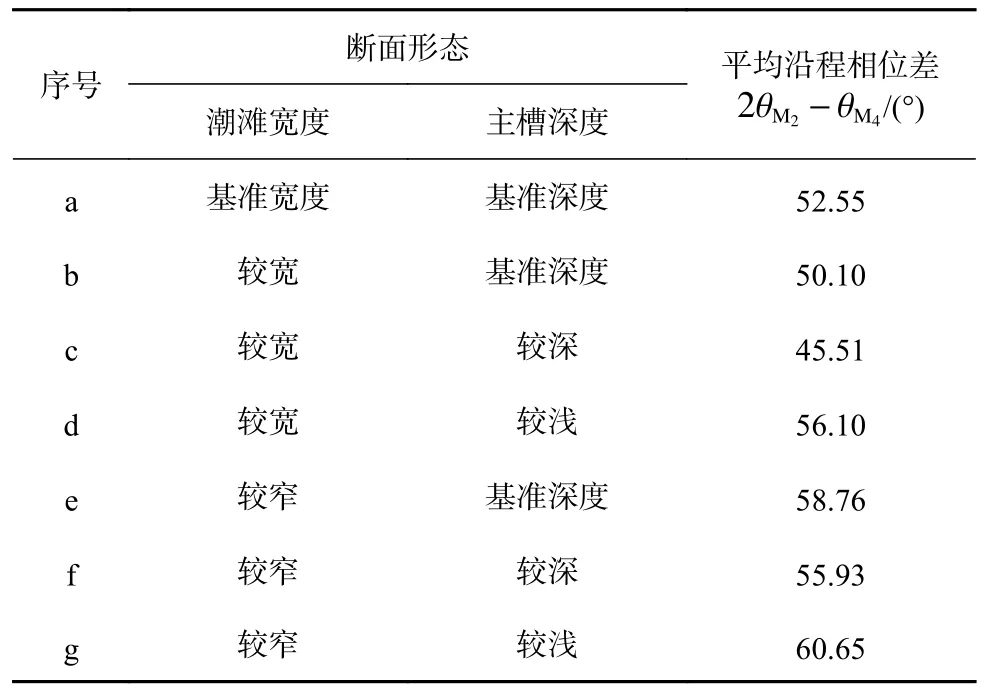
表4 不同断面形态河口的沿程相位差均值Table 4 The along-channel averaged relative tidal phases of estuaries with different cross sections
断面形态的改变会引起不同的能量耗散。由于摩擦系数与流速有关,断面面积减小,流速增大,摩擦系数增大,能量耗散加剧,从而导致涨落潮历时不相等,河口更倾向于涨潮主导[37,42-43]。上述结果表明,河口地貌对潮汐不对称性的产生和发展有着重要的影响,当纳潮量相同时,潮滩缩窄使得断面面积减小,流速加大,涨潮历时减短,因此窄潮滩倾向于涨潮主导,宽潮滩倾向于落潮主导,同理,浅主槽倾向于涨潮主导,这也进一步验证了文献[11,44-46]的相关发现。
4 平面形态改变对潮汐不对称性的影响
为了使不同模型之间的纳潮量相等,设计的3 个模型的平面形态以及长度均不相同,但口门处的断面是相同的并且沿程水深相等。同样,对水位进行调和分析,可以得到3 个不同平面形态河口相位差2θM2-θM4的沿程变化(图6)。

图6 不同平面形态的相位差2θM2-θM4沿程变化Fig.6 Changes of relative tidal phase along the channel in estuaries with different plan forms
潮滩面积从大到小依次为矩形平面河口、线性变化平面河口和指数型收缩平面河口。为了使纳潮量相同,河口的长度则依次增加。当纳潮量相同时,虽然河口的平面形态、长度有所不同,但整体依旧是倾向于涨潮主导。经计算,指数型收缩平面、线性变化平面以及矩形平面的平均沿程相位差2θM2-θM4分别为32.73°、13.37°和6.68°(表5),其中,长度最短的矩形平面河口的涨潮主导最弱,线性变化平面河口其次,长度最长的指数型收缩平面河口涨潮主导最强。由于3 种河口在口门处的断面相同,因此在口门附近三者的相位差2θM2-θM4相差不大。随着潮波继续向内传播,由于矩形平面的河口宽度沿程不变,不会产生较大的由于平面形态改变而带来的能量聚集,加之长度短,易受径流的影响,涨潮流流速的增速逐渐减缓,沿程相位差2θM2-θM4从口门处的2.9°增加到9.34°后逐渐趋于平缓。线性变化平面的河口同样也由于长度较短,径流影响大,因此在河口长度的前1/3 段由口门处的3.21°增加了7.39°到10.6°,而后1/3 段相位差仅由17.89°增加了2.94°到20.83°,增幅减弱。而指数型收缩平面沿程缩窄较快,使得涨潮流速不断增加,从而导致沿程相位差2θM2-θM4由3.05°不断增大至59.23°,又因为径流端的宽度窄,径流流速较大,削弱了涨潮流速,使得相位差2θM2-θM4在靠近径流端处由59.23°减小至52.79°。

表5 不同平面形态的沿程相位差均值Table 5 The along-channel averaged relative tidal phases of estuaries with different plan forms
从余流场看,在纳潮量相同时,平面形态的改变会导致潮滩与主槽的余流流速不同(图7)。虽然不同河口的沿程相位差在口门附近的差异不大,但余流流速不同。指数型收缩平面的河口主槽流速明显大于线性变化平面河口与矩形平面河口,并且随着河口平面形态的不断缩窄,主槽的余流流速逐渐增加。对于线性变化的河口而言,由于河口平面形态的变化并不剧烈,因此主槽的余流流速增加并不显著。矩形平面河口的主槽内余流流速最小。而对于潮滩而言,平面形态的缩窄会导致潮滩余流流速减小,这表明在纳潮量相同时,河口宽度的快速缩窄会加大主槽的余流流速,减小潮滩的余流流速。
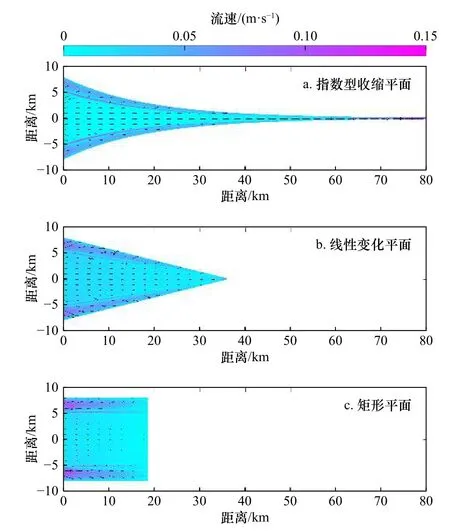
图7 不同平面形态河口的余流场Fig.7 Residual currents in estuaries with different plan forms
随着河口收缩率的增加,潮波变形加剧,流速和波长增加,涨潮主导增强[30-31]。在实际河口中,河口的平面形态大多沿程发生收缩(图8,图9)。下面通过强收缩的指数型收缩河口和弱收缩的指数型收缩河口两种不同收缩率的河口来讨论河口平面形态的不同收缩率对于潮汐不对称性的影响。为了消除长度带来的影响,将河口长度固定为80 km。虽然收缩率不同,但两者均为涨潮主导型。相位差均沿程缓慢增加,强收缩河口的沿程相位差大于弱收缩河口的沿程相位差,弱收缩平面和强收缩平面的平均沿程相位差2θM2-θM4分别为21.40°和32.73°,这意味着当河口的平面收缩率较大时,由于断面的快速缩窄导致涨潮流速增大,此时河口相较于收缩率较小的情况下更倾向于涨潮主导型。从余流图来看,平面形态的收缩会改变潮滩的落潮主导情况,随着收缩率的加剧,潮滩向落潮方向的余流流速转向涨潮方向。并且随着收缩率的增加,主槽的流速逐渐减小,潮滩的流速逐渐增加。从上述研究可以看出,河口平面形态对潮汐不对称性的影响本质是由平面形态改变引起沿程断面形态变化造成的。本发现也进一步验证了其他相关研究,表明平面收缩较强的河口更倾向于涨潮主导[13,30]。
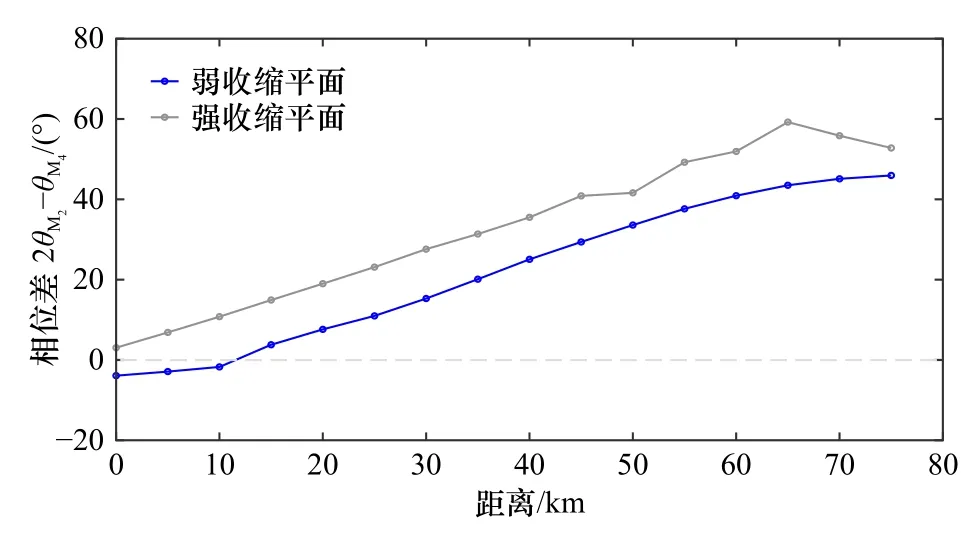
图8 不同平面收缩率河口的相位差2θM2-θM4沿程变化Fig.8 Changes of relative tidal phase along the channel in estuaries with different convergence

图9 不同收缩率河口的余流场Fig.9 Residual currents in estuaries with different convergence
5 结论
本文通过二维水动力模型模拟了不同断面形态和平面形态的理想河口水动力情况,从流速、相位差和余流3 方面进行了分析,主要得出以下3 点结论。
(1)主槽深度会影响沿程相位差出现峰值的位置和大小,较深的主槽能使峰值出现较晚且峰值更大。此外还会影响最大落潮流速以及落潮历时,主槽越浅,最大落潮流速越小,落潮所需历时越长,河口更倾向于涨潮主导。潮滩大小的变化对潮汐不对称性的影响在主槽较深时更显著。窄潮滩倾向于涨潮主导型,宽潮滩倾向于落潮主导型。此外,相较于主槽较浅的河口,潮滩大小的变化对潮汐不对称性的影响在主槽较深的河口中更为显著。
(2)在纳潮量相同的情况下,本文设置了矩形、指数收缩型以及线性变化3 种平面形态。在沿程水深不变的情况下,平面形态的改变不会影响河口整体的涨落潮主导趋势。顺直且较短的河口涨潮主导最弱,而平面形态沿程收缩且长度较长的河口涨潮主导型最强。此外,河口宽度沿程缩窄会加大主槽的余流流速,减小潮滩的余流流速。
(3)收缩型河口的相位差沿程缓慢增加。收缩较强的河口相较于弱收缩河口沿程相位差更大,其涨潮主导特性更为显著。随着河口平面收缩率的增强,主槽的余流流速减小,潮滩余流流速增大,潮滩的涨潮主导增强。
最后,值得一提的是河口水动力、泥沙、地貌三者相互作用,处在一个动态变化的过程中。本文尚未考虑泥沙输运及其引起的地貌演变,未来研究可将泥沙引入,进一步揭示河口地貌演变与潮汐不对称性变化的互馈机制。

