高耸建筑物折叠爆破上下缺口起爆间隔时间简易确定方法
康永辉,韩博敏
(1.新疆维吾尔自治区公安厅治安管理总队基层基础工作支队,新疆 乌鲁木齐 830000;2.新疆维吾尔自治区工程爆破协会,新疆 乌鲁木齐 830000)
高耸建筑物爆破拆除,依据周边环境允许原则和有害效应控制在允许范围的原则,有以下几种倒塌方式:定向倒塌、原地坍塌、逐跨坍塌、折叠倒塌。当场地允许倒塌范围小于建筑物高度的1.2倍时,或因减振解体等方面要求,高耸建筑物大部分须要采用折叠倒塌。折叠倒塌又分为单向折叠、双向折叠、异向折叠、内向折叠。无论那种折叠倒塌方式,在倒塌过程中上下折叠段均处于运动状态,要确保既定的倒塌方向、倒塌范围,所需要的爆破技术相对定向倒塌更为复杂,需要精心设计和精心施工。
1 折叠爆破上下缺口起爆间隔时间确定非常重要
折叠爆破拆除失败甚至出现事故,在技术设计上主要原因:一是上下爆破缺口的参数设计不当;二是上下爆破缺口起爆的延期时间设计不当。而上下缺口起爆延期时间间隔选取不当会导致折叠爆破拆除有两方面风险:一是上下缺口起爆延期间隔时间太短上段还未形成明显的倒塌趋势,下段起爆,导致上段倒塌方向不准,如图1所示;二是上下缺口起爆延期间隔时间太长,如双向折叠式,钢筋混凝土高耸建筑物,在钢筋的牵拉作用下,上段会带动下段会倒向相反的方向,如图2所示。这些情况都容易会造成事故。
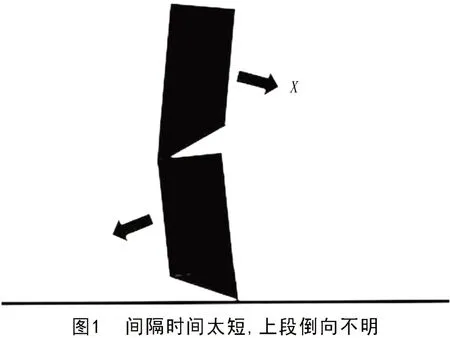
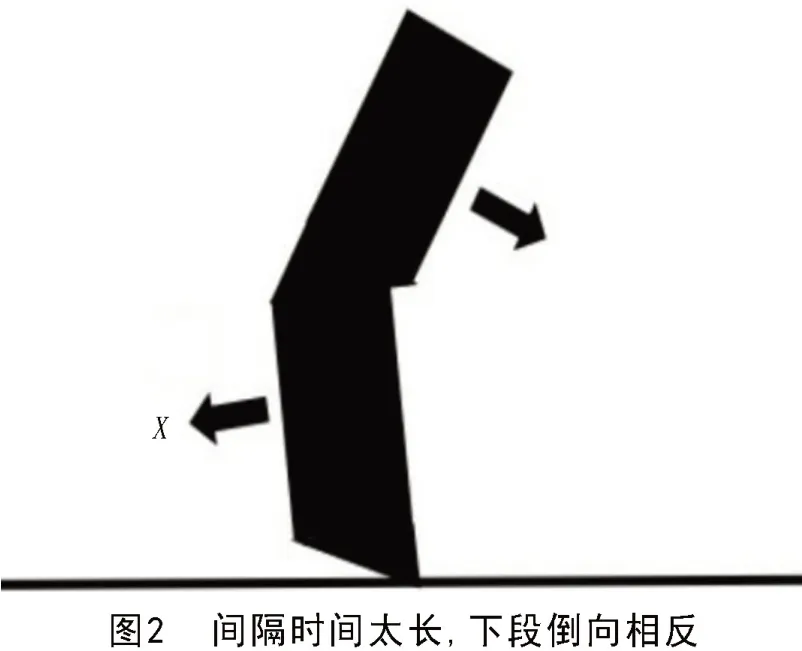
2 如何用简易方法确定折叠爆破上下缺口起爆间隔时间
上下缺口起爆延期时间间隔的主要依据由两个方面确定:一是避免上段建筑物塌落时后座,保证初始阶段的倾倒方向;二是两段建筑物折叠及落地状态满足要求。据此,确定上下缺口合理起爆时间间隔:①应使上缺口首先形成,并且保证下缺口起爆时,上部建筑物已形成定向倾倒的趋势,在上下缺口时间间隔的选择过程中可以考虑允许上段建筑已偏转1°~2°;②在支撑断面整体发生屈服破坏以前,下部缺口必须起爆;③在上缺口位置确定的条件下,选择合理起爆时间间隔,使高耸建筑物落地状态到达预定的效果。另外,下缺口起爆后,由于下端建筑物体产生加速度,上段筒体的后坐力会降低,说明缩短起爆时间间隔有利于防止上段筒体的后坐,因此保证上端建筑物倒塌趋势形成前提下,尽量缩短上下缺口之间的起爆时间间隔。
钢筋混凝土烟囱是典型的高耸建筑物,下面以钢筋混凝土烟囱折叠爆破为例,分析上下段延期间隔时间。钢筋混凝土烟囱折叠爆破上段倾倒运动原理,类似于细棒倾倒运动原理,但远比细棒倾倒运动复杂很多:一是细棒线密度均匀,烟囱外形上细下粗,烟囱壁上薄下厚,其转动惯量计算复杂;二是细棒倾倒力矩只是重力力矩,钢筋混凝土烟囱倾倒力矩是重力力矩与钢筋抗弯力矩共同的合外力矩,且重力力矩随烟囱倾倒角度变大而非线性增大,钢筋抗弯力矩随烟囱倾倒角度变大而非线性减小。因此精确计算高耸建筑物折叠倒塌运动需要借助计算机仿真技术进行计算,但由于高耸建筑物折叠爆破爆破缺口上部建筑物已形成定向倾倒的倾倒角度较小,可以用细棒倾倒运动简化计算,达到其合外力矩可用重力力矩乘以一个系数,做近似处理。这样运算结果仍具有较高的精度,可以为工程设计提供参考。
如图3所示,钢筋混凝土烟囱倾倒力矩是重力力矩与钢筋抗弯力矩共同的合外力矩。
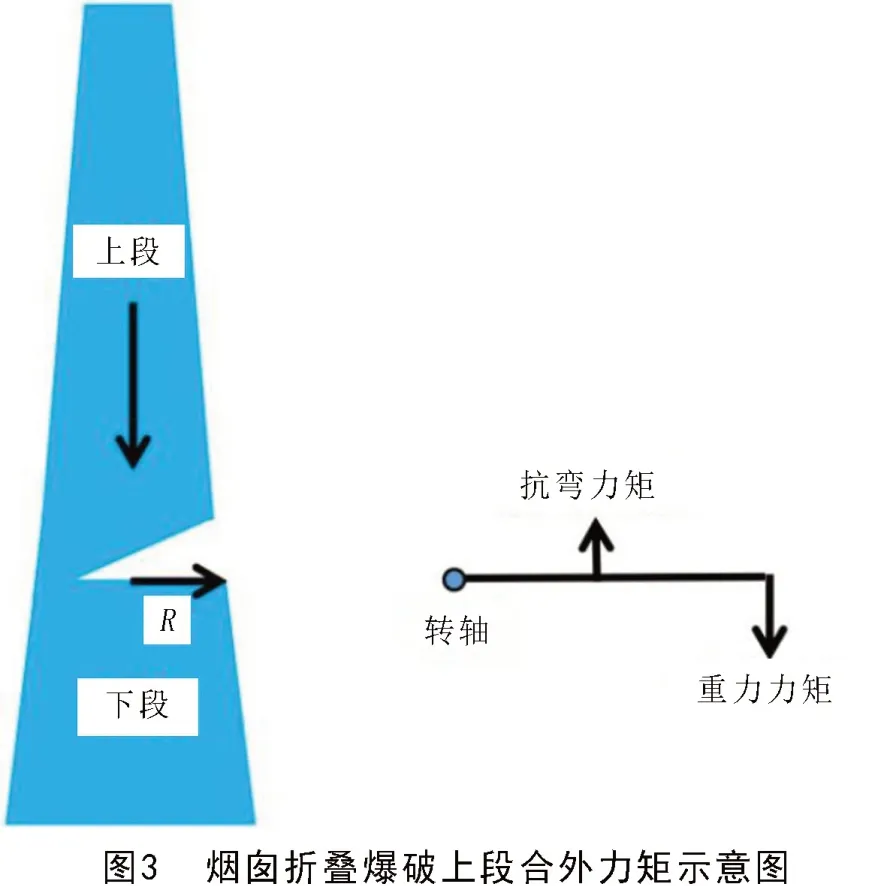
此处将合外力矩简化为重力力矩乘以系数K,设钢筋混凝土烟囱爆破缺口缺口圆心角230°。
则切口处合外力矩:

式中:M——力矩,m·N;
K——系数;
m——细棒的质量,kg;
R——缺口处烟囱半径,m。
因重力力矩随烟囱倾倒角度变大而非线性增大,钢筋抗弯力矩随烟囱倾倒角度变大而非线性减小,烟囱上段要形成定向倾倒的趋势,烟囱上段允许偏转角度为1°~2°,此处简化计算合外力矩取其在允许偏转角度范围概算均值。
则式(1)中:
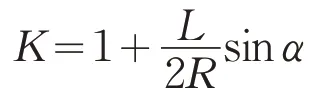
式中:L——细棒长度,m;
ɑ——1°~2°。
转轴通过细棒端点转动惯量:

式中:I——转动惯量;
m——质点质量,kg;
L——细棒长度,m。
角加速度与合外力矩的关系:

式中:M——合外力矩,m·N;
I——转动惯量;
β——角加速度,r/s2。
偏转角度:

式中:α——角度,r;
T——转动时间,s;
β——角加速度,r/s2。
将(1)、(2)、(3)式结果代入(4)式可得:

式中:T——转动时间,s;
α——偏转的角度,r;
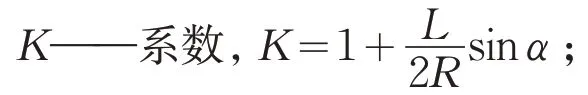
ɑ——1°~2°;
R——缺口处烟囱外径,m。
上式中转动时间即为上下缺口最佳间隔时间。因此(5)式即为确定折叠爆破上下缺口起爆间隔时间简易公式。
3 折叠爆破工程实例验证简易公式实用性
以编入《爆破设计与施工》(王旭光主编)的钢筋混凝土烟囱折叠爆破工程实例[1]进行验证。该钢筋混凝土烟囱高度100m,设计总体方案为双向三折叠爆破拆除:上缺口在+60.2m处,缺口圆心角230°,爆破缺口处烟囱外径5m,上段+60.2~+100m;中缺口+30.2m处,缺口圆心角230°,爆破缺口处烟囱外径6m,中段+30.2~+60.2m;下缺口+0.5m处,缺口圆心角240°,爆破缺口处烟囱外径8.0m,下段+0.5~+30.2m;缺口之间的时差,选择上缺口起爆时刻为0s,中缺口起爆时刻为1.35s,下缺口起爆时刻为2.4s。
用简易公式计算上缺口与中缺口起爆间隔时间:将α=2°=0.0349r;R=2.5m;L=35m(等效长度)代入:

即计算得上缺口与中缺口起爆间隔时间1.49s,而实际爆破工程上缺口与中缺口起爆间隔时间1.35s,误差10%。
用简易公式计算中缺口与下缺口起爆间隔时间:将α=2°=0.0349r;R=3.35m;L=26m(等效长度)代入:

即计算得中缺口与下缺口起爆间隔时间1.0s,而实际爆破工程中缺口与下缺口起爆间隔时间1.05s,误差5%。

