灰色预测模型GM(1,1)在国内安全生产事故预测中的应用

周明星，房栋

1.河南牧业经济学院工商管理学院，河南，郑州，450044；2.郑州大学土木工程学院，河南，郑州，450000

0 引言

安全生产重于泰山，人民群众的安全利益高于一切，我国每年因交通、爆炸、火灾等安全事故导致了大量的人员伤亡和重大的经济损失，给社会带来了许多负面影响，安全生产问题已然变成了全社会的热门话题之一[1]，科学、合理地对安全生产事故的发生和发展进行预测也成为了安全生产研究的一项重要任务。

灰色预测模型GM(1,1)是一个依据小样本数据建立的一阶一元微分方程，由于所需数据少、原理简单、计算方便、预测结果精度高、可靠性高等优点，被广泛地应用于工程控制、经济管理、未来学研究、社会系统、生态系统及复杂的农业系统中[2]。

为了更好地总结事故教训，探究伤亡事故发生的规律，本文应用GM(1,1)模型对国内安全生产事故的发展趋势进行了预测。基于2012～2021年国内安全生产事故数据，建立了事故伤亡人数和发生起数的灰色预测模型，对比分析计算值与实际值，验证了灰色预测模型GM(1,1)应用于安全生产事故数据统计分析的可行性和可靠性。在此基础上，预测了2022～2030年国内安全生产事故伤亡人数，为制定安全生产政策和减少事故的发生提供了决策依据。

1 事故数据统计与分析

根据2012～2021年《安全与环境学报》中与国内安全生产事故统计分析有关的论文[3-4]，统计了2012～2021年国内安全生产事故总体情况，如表1所示。

由表1可知，2012～2021年我国共发生安全生产事故6712起，死亡26220人。从2012～2021年，事故的数量和死亡人数在逐年下降，发生起数从1040起降低到353起，降低了66.1%；死亡人数从4462人降低到1129起，降低了74.7%。从总体情况来看，这十年内我国国内安全生产形势明显好转。

表1 2012～2021年国内安全生产事故总体情况统计表

2 事故数据处理

2.1 事故伤亡人数灰色预测模型GM(1,1)

（1）事故伤亡人数灰色模型GM(1,1)的建立。由表1各年事故伤亡人数，确定原始数据序列：

对原始数据序列进行累加处理，得到一次累加序列：

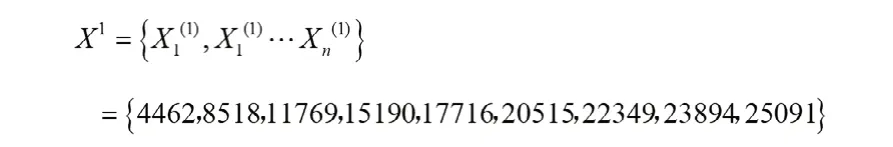
建立数据矩阵，计算a和u。

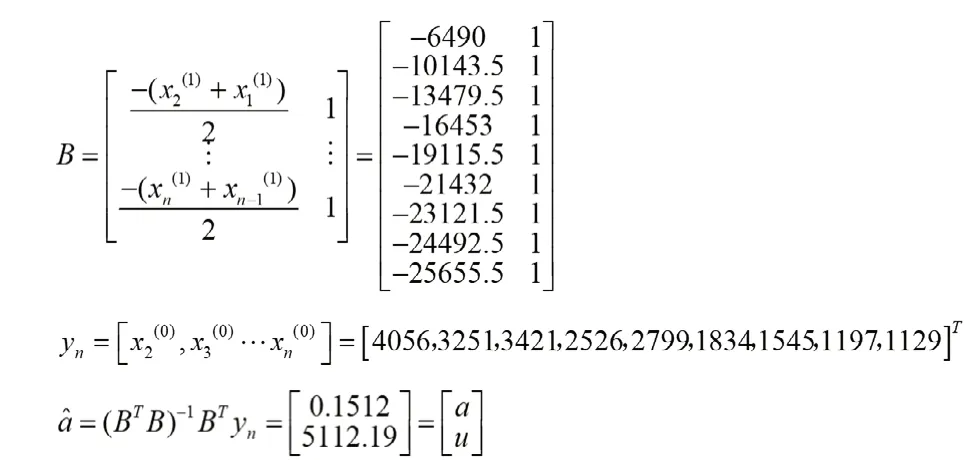
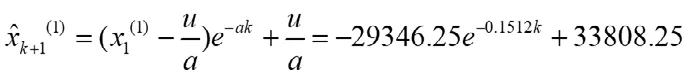
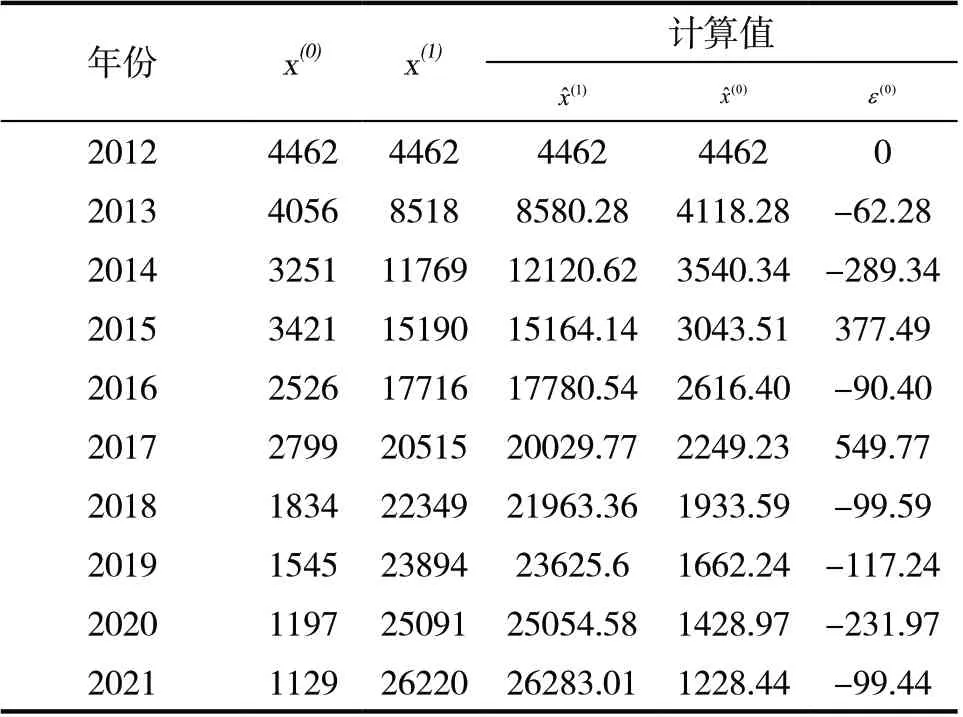
表2 2012～2021年国内安全生产事故死亡人数预计算值

（2）事故伤亡人数灰色模型GM(1,1)的检验。选用后验差法检验灰色预测模型GM(1,1)的精度，对照表3，确定该灰色预测模型GM(1,1)的精度等级。

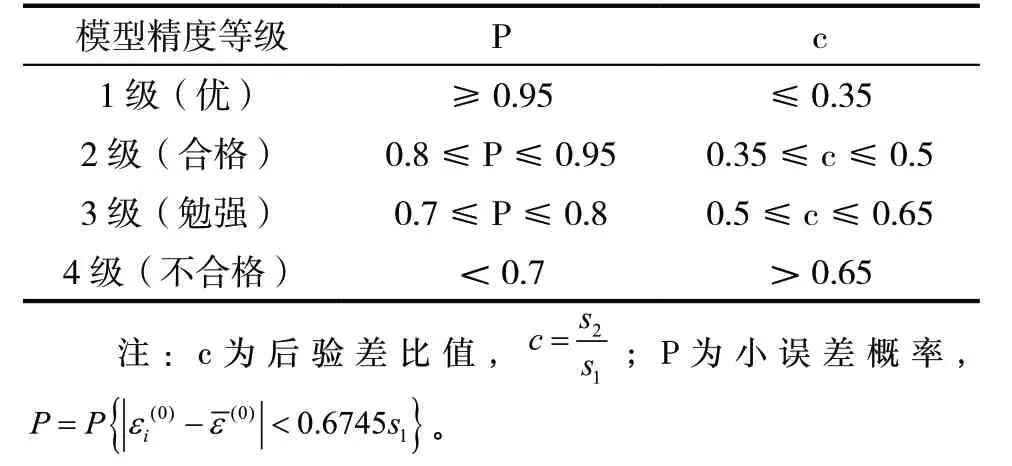
表3 模型精度等级判定标准

最后，根据计算得到的c和p，对照表3，确定该灰色预测模型GM(1,1)精度等级为优，预测结果可靠。

2.2 事故发生起数灰色预测模型GM(1,1)

对照表3，确定该灰色预测模型GM(1,1)精度等级为二级，精度不高。在此基础上，对事故起数预测模型进行修正。

（3）事故发生起数灰色模型GM(1,1)的修正。对表4中的残差ε(k)进行非负处理，按同样的方法，建立残差预测模型：

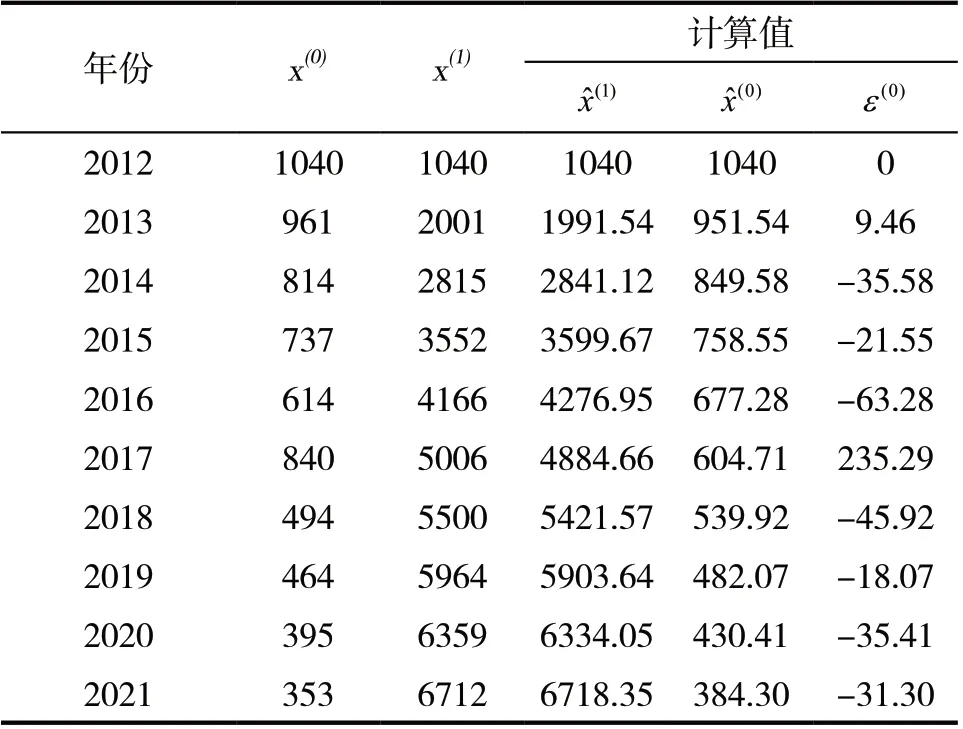
表4 2012～2021年国内安全生产事故发生起数计算值

根据残差预测模型，对原模型进行修正，得到第一次残差修正后的模型：

残差修正后的预测值如表5所示。

表5 第一次残差修正后预测值

一次残差修正后进行模型精度检验得到：残差均值=27.42，残差方差=3441.69，比值c=0.24，小概率误差P=0.9，模型预测等级二级，精度不高。在此基础上，对事故起数预测模型进行二次残差修正[5-6]。

对表5中的残差ε(k)进行非负处理，按同样的方法，建立二次残差预测模型：

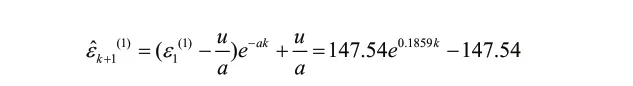
根据二次残差预测模型，对原模型进行修正，得到第二次残差修正后模型：

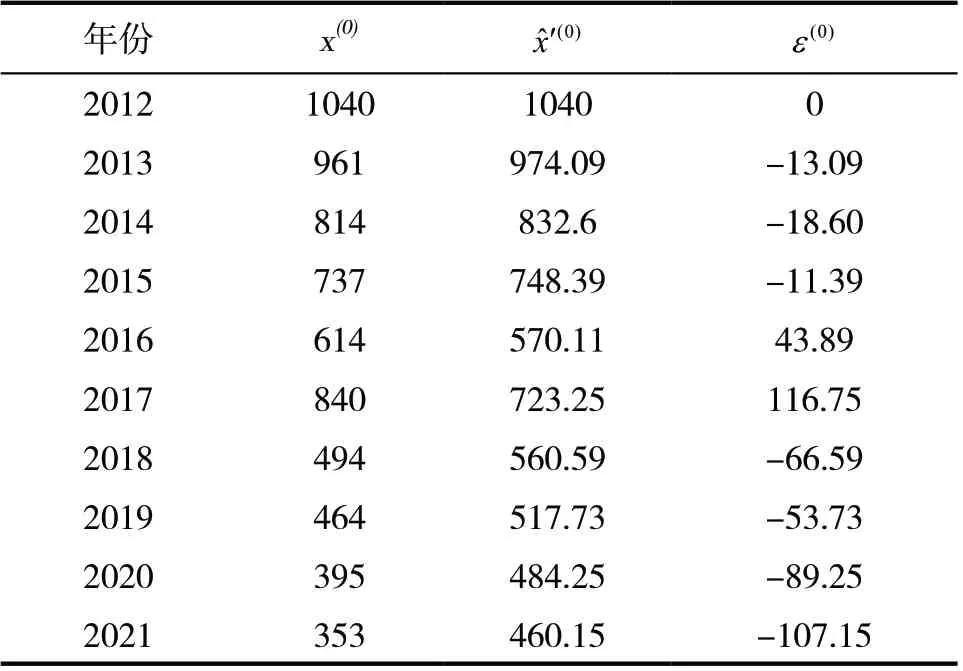
表6 第二次残差修正后预测值

二次残差修正后进行模型精度检验得到：残差均值=-19.92，残差方差=4333.97，比值c=0.27＜0.35，小概率误差P=1，模型预测等级一级，预测结果可靠。

3 事故伤亡数据预测

相较于事故发生起数，我们更为关心事故伤亡人数的预测值。根据事故伤亡人数灰色预测模型，计算得到2022～2030年事故伤亡人数预测值，如图1所示。

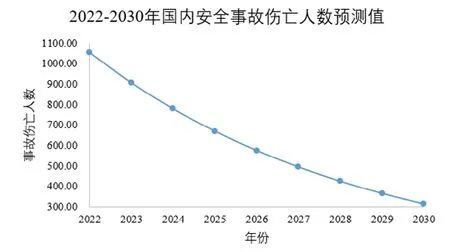
图1 2022-2030年国内安全生产事故伤亡人数预测值

由图1可知，2022～2030年国内安全生产事故预测伤亡人数是逐年下降的，且相比2022年，2030年伤亡人数下降了70.2%[7-8]。

4 结论

本文基于2012～2021年国内安全生产事故数据，建立了事故伤亡人数和发生起数的灰色预测模型GM(1,1)，根据模型得到2012～2021各年事故的计算值[9]。通过对比分析各年事故的计算值与实际值，验证了灰色预测模型GM(1,1)应用于安全生产事故数据统计分析的可行性和可靠性。在此基础上，预测了国内安全生产事故的发展趋势。结果表明，灰色预测模型GM（1,1）可用于预测国内安全生产事故的变化规律和发展趋势。