基于排队论的反无人机集群武器部署优化方法

高志刚，刘艳彬，陈长远，冯宇，张雨泽

（1.中国人民解放军93196部队，乌鲁木齐 841700；2.空军工程大学 航空工程学院，西安 710038）

近些年来，随着国内外航空技术的发展，以及网络、人工智能等前沿技术的不断进步，无人机因其成本低，体积小，机动性高，可代替人执行“枯燥、恶劣、危险、纵深”（Dull、Dirty、Dangerous and Deep，4D）任务等诸多优势得到了迅猛发展。越南战争中，“火蜂”无人机第一次在实战中投入使用，该无人机在战场上的出色表现使人们认识到了无人机的新价值。在之后的海湾、阿富汗以及伊拉克战争中，美方接连使用过“捕食者”、“全球鹰”和“猎人”等数十种无人机参与战斗，在与有人机的数据对接、情报侦查和毁伤评估等方面起到了至关重要的作用。随着未来作战范围的日益扩大和战场环境的日趋复杂，我们需要对战场有多位一体、全域覆盖精确细致的感知能力，单架无人机显然不能满足该作战需求，因此国内外军方和研究人员将更多人力、财力和精力放在了无人机集群协同作战上面。无人机集群可搭载不同功能模块来实现能力互补，通过数据链进行信息的交互与共享。与此同时，其无中心化和自主化等诸多优势能够有效地提高整体作战效能，近年来已经由概念变成了现实。2018年1月6日，叙利亚反对派首次使用13架装有爆炸物的攻击型无人机对俄罗斯驻叙利亚赫迈米姆空军基地和塔尔图斯海军基地展开了集群式攻击。虽然此次袭击没有对俄方人员造成较大的人员伤亡和财产损失，但无人机集群已经展现出巨大的作战潜力。2019年9月14日，也门胡塞武装使用18架装载导弹的无人机通过协同分工对沙特阿美石油公司的2处油田进行了袭击，导致多处石油设施发生连环爆炸，并燃起大火，袭击后，无人机集群还对目标进行了毁伤效果评估。2019年3月14日，伊朗革命卫队在波斯湾海域使用近百架无人机编队进行了大规模实兵演习，该编队在成功飞行1 000 km后，对制定目标进行摧毁，取得了显著的作战效果。美国早在20世纪90年代末期就提出了无人机集群作战的构想，进行了大量的试验研究，近年来也相继启动了多个无人机集群项目，并希望在2036年实现无人机集群作战。比如“小精灵”项目，提出了在运输机上发射大量分布式小型无人机，用于执行查打任务，并在任务完成后进行回收，可实现无人机集训的快速部署和重复利用。“山鹑”项目，美国在该项目基础上成功完成了103架山鹑无人机以0.6马赫速度的投放，并演示了编队飞行和集群侦查决策等群体行为。

这些事件都表明了随着相关研究的不断深入和技术运用的日趋成熟，无人机集群作战在未来战争中将扮演重要的角色，对未来战场攻防局势的影响也将越来越大。换而言之，无人机集群带给我们的威胁也将越来越大，势必会给重要区域的防空系统带来严峻的挑战。我们需要根据来袭无人机集群达到的方向、密度、时间等多个因素来对防空武器进行部署，如果一味追求数量，则会造成武器资源的浪费和分配不均匀；如果数量过少或者依靠单一的防空武器和单层防线很难对来袭无人机集群实施有效的拦截打击，极可能完成不了拦截任务，使我方处于危险境地。因此，面对复杂动态的无人机集群，如何合理部署防空武器，提高拦截概率，降低防御成本，充分发挥其作战效能是目前反无人机集群作战研究中亟待解决的关键技术之一。

本文立足我国当前军事形势，考虑了由远程、中程和近程防空武器所构成的防空系统，基于防空武器效能分析中常用的排队论模型，对3层防线层层建模，描述来袭无人机集群进入防线的过程，建立突防概率模型，并进行求解。在此基础上，提出了最少防空武器数量的“理想区”模型和最低防御成本的“最优解”，最终得到了同时满足来袭无人机集群指定突防概率条件下防空武器数量最小化和拦截成本最低化的部署优化方法，具有较强的工程应用价值。

1 反无人机集群的排队论模型

1.1 排队论简介

排队论是现代防空武器效能分析中应用较为广泛的一种方法。该方法最早起源于对电话通信排队连线的研究，当时也叫作话务理论。直到二战以后，各国学者开始为其赋予工程价值，并广泛应用于军事、服务、运输等重要领域，展现出强大的生命力。排队论主要包括4个指标：输入过程、服务规则、服务机构和服务时间，这4个指标构成了排队论的基本要素。

在对来袭无人机集群进行防御的过程中，防空系统就是“服务机构”，无人机集群中的每个作战单元就是“顾客”，打击过程就是“服务过程”，射击时间就是“服务时间”，所采取的防空策略就是“服务规则”。因此，当无人机集群要突破防线时，整个防空系统可以看作一个服务台，遵循“先到先服务”的原则对其进行防空打击，但如果该防线上的所有武器都在进行对敌打击，则后到的无人机作战单元可以视为在杀伤区逗留过长时间未被射击从而突防成功。从排队论角度上讲，可以理解为当无人机集群强度超过“服务规则”下的服务能力后，“顾客”就不会再继续等待，从而放弃服务，因此就可以判定没有达到“服务效果”，即无人机集群突防成功。

1.2 基本假设

1）输入过程。对于防空系统来讲，无人机集群具有数量多、个体分散、航路不确定以及机动性强等特点，集群中每个作战单元来袭的时间、方向、密度等都是随机的，具有排队论中“顾客流”的性质。将进入防空区域无人机集群中的每个作战单元看作是泊松流，其来袭相隔时间服从参数为的负指数分布，如式（1）所示。对于第1层防空系统，输入目标为集群中所有来袭单元，第2层为已经突破第1层防线的来袭单元，依次类推，如图1所示。

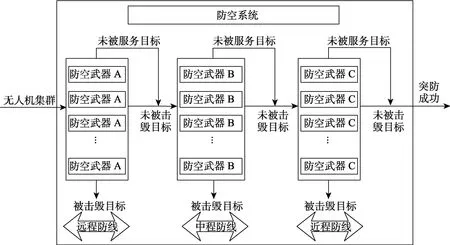
图1 3层防空系统的排队模型 Fig.1 Queuing model of three-tier air defense system

式中：为单位时间内到达的无人机集群作战单元平均数目，即来袭密度；1/为来袭目标的平均到达间隔时间。

在时间内，个无人机集群作战单元到达的概率服从泊松分布，如式（2）所示。

2）服务规则。防空系统对于无人机集群中作战单元的射击服从“先到先服务”的原则，如果同时到达，则服务顺序任意。为了方便计算，每架无人机只被1个防空武器射击，且只射击1次，不采用多个防空武器对1架无人机同时射击的方式。对于突破该层防线的飞机，分为2种情况：在单位时间内防空武器全在工作，即系统处于“忙碌”状态，该飞机未被射击；飞机虽然被射击，但未被击落，仍然突破防线，涉及到防空武器的毁伤率问题。

3）服务机构。根据现代防空作战实践证明，单层防线或者单一防空武器难以应对密集且无序的来袭敌机，通常采用不同类型防空武器的混编作战，构成远、中、近程立体化防空体系，相互取长补短，形成严密的对空火力。本排队论模型的服务机构是由远程防空武器A、中程防空武器B和近程防空武器C所组成的防御系统，分别担任远程、中程和近程防线的防御任务，如图1所示。远程防空武器A可以在最外层防线直接拦截来袭无人机集群，起到先发制人的效果；中程防空武器B主要是对已经突破最外层防线的无人集群作战单元进行拦截，使其能够远离投弹区域，阻断其投弹任务；近程防空武器C部署于重点防护目标附近，主要用于拦截具有自杀式行为的无人机及其投放的导弹等武器。

4）服务时间。防空系统作为服务机构，服务时间即射击周期sj与来袭无人机达到间隔时间一样，服从参数为的负指数分布，即：

式中：为单位时间内射击的来袭目标平均数，即服务率；1/为防空武器对来袭目标的平均射击周期。

2 模型建立与求解

根据现代防空作战特点，从影响作战结果的角度出发，主要选取无人机集群未被射击概率、突防成功概率和突防后密度3个评价指标进行建模，结果具有直观的现实意义。由于本文是3层防线组成的防空系统，需要对每层防线层层建模，过程相互独立，又紧密联系，模型不仅适合3层防线，对于采用本文作战规则下的层防线也同样适用。本文的最终优化结果，也是建立在本文排队论的基本假设和服务规则下进行优化的结果。

2.1 第1层防线

对于第1层防线，假设共有套远程防空武器A，无人机集群通过该防线时作战单元数量为。根据1.2节基本假设，其目标流的来袭相隔时间服从参数为的负指数分布，防空武器的射击周期服从参数为的负指数分布。这时可以将该情况看作位顾客、个服务台的排队系统，基于排队论模型，利用爱尔朗公式，无人机集群作战单元未被射击到的概率为：

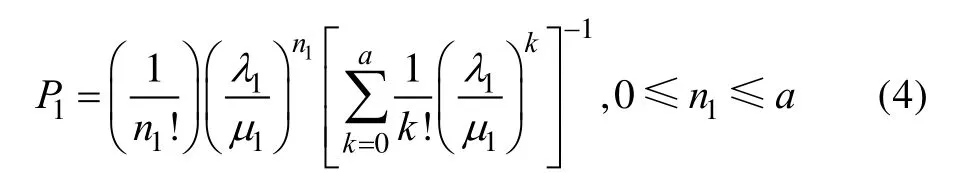
式中：表示第1层服务台工作的数量，即正在进行射击的远程防空武器A的数量。

1.2节已指出，突防成功的无人机作战单元主要包括未被射击的无人机以及遭遇射击后仍突防成功的无人机。设防空武器A对无人机集群的毁伤率为，则可得到无人机集群突破第1层防线的概率为：

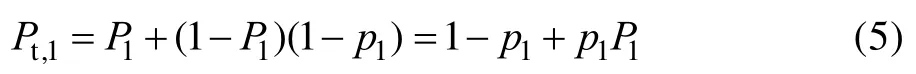
无人机集群的突防数量也是接下来要达到第2层防线的来袭数量，其数学期望为：

无人机集群突破第1层防线时的毁伤数量为：

2.2 第2层防线

此时，第2层防线由套中程防空武器B组成，无人机集群中的每个作战单元视为泊松流，来袭密度为，通过该防线时数量为，经过第1层防线的筛选，可以得到：

假设防空武器B的射击周期服从参数为的负指数分布，这时可以将该情况看作位顾客、个服务台的排队系统，则无人机集群作战单元未被射击到的概率为：

式中：表示第2层服务台工作的数量，即正在进行射击的中程防空武器B的数量。

设第2层防线防空武器B对无人机集群的毁伤率为，则可得到无人机集群突破第二层防线的概率为：

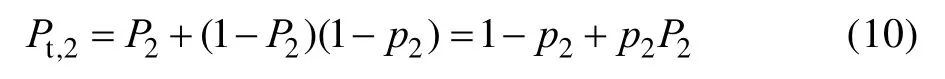
突防数量为：

毁伤数量为：

2.3 第3层防线

第3层防线由套近程防空武器C组成，经过第2层防线的再次拦截后，进入第3层防线的无人机集群中的每个作战单元仍视为泊松流，来袭密度为，通过该防线时的数量为，可以得到：

假设防空武器C的射击周期服从参数为3的负指数分布，这时可以将该情况看作位顾客、个服务台的排队系统，则无人机集群作战单元未被射击到的概率为：

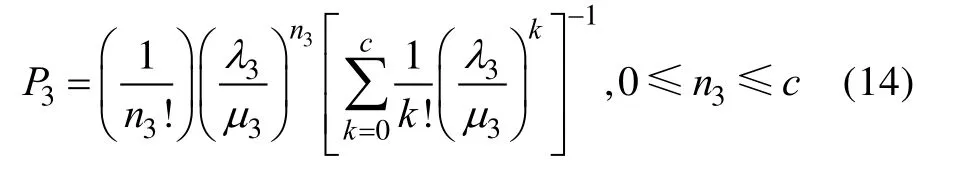
式中：表示第3层服务台工作的数量，即正在进行射击的近程防空武器C的数量。

同理，设第3层防线防空武器C对无人机集群的毁伤率为，则可得到无人机集群突破第3层防线的概率为：

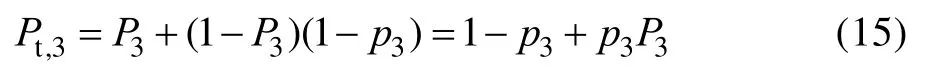
由于本层防线为最后一道防线，完成突防的作战单元意味着最终突防成功，其数量用来表示：

毁伤数量为：

2.4 第m层防线

为了使模型具有普遍性，根据上述3层防线各个指标的求解，可推广得到当防线有层时，各个指标的通用表达式。无人机集群作战单元在第层防线未被射击概率P为：

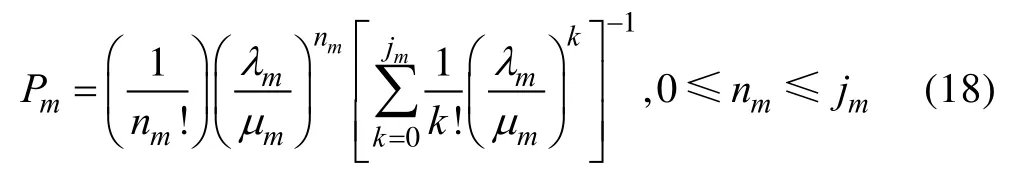
式中：j为第层防线防空武器数量；n为该防线正在射击的防空武器数量；λ为来袭密度；1/为防空武器对来袭目标的平均射击周期。

无人机集群突破第层防线的概率为：

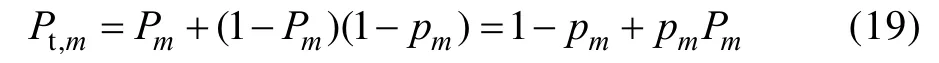
式中：p为第层防线防空武器对无人机集群的毁伤率。

第层防线突防数量为：

式中：N为第层防线突防数量，也是第1层防线的来袭目标数量。

第层防线的毁伤数量为：

3 仿真分析

3.1 案例求解

在某次要点夺控行动中，红方使用无人机集群对蓝方某个区域内的重点防护目标进行突袭，蓝方设置远、中、近3层防线，防空武器分别为A、B和C 3种类型，其射击周期分别服从参数为=1、=和=4的负指数分布，每类武器在同一时间只能对一个来袭目标进行射击，具体参数见表1。假定来袭的无人机集群中的每个作战单元符合泊松流形式，来袭密度=8架/min，来袭时间为8 min，来袭总数为64架。如果要求来袭目标的最终突防概率不大于0.1，现有防空武器能否满足，若满足要求，优化其兵力部署。

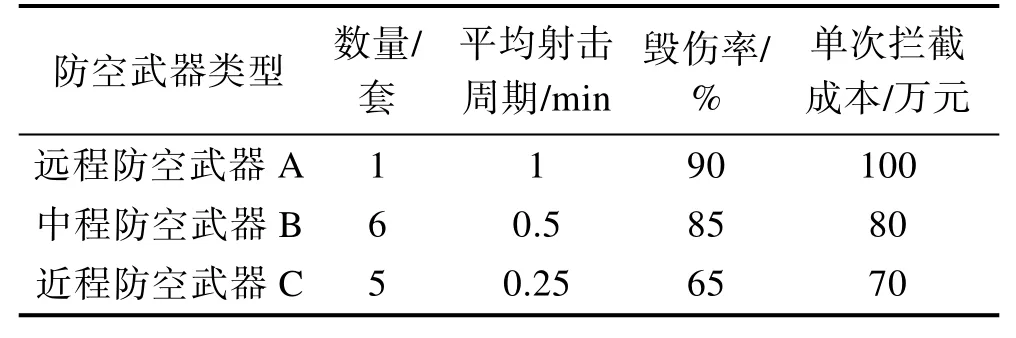
表1 防空武器参数 Tab.1 Air defense weapon parameters

利用第2节所建立的模型，对每层防线的防空效能进行层层求解，得到无人机集群通过每层防线时的未被射击概率、突防成功概率和突防后密度，见表2。

从表2中结果可知，在现有防空武器装备所构成的三层防空系统下，来袭无人机集群的最终突防概率为7.1%，能够满足不大于0.1的突防概率要求。同时，可以发现利用本文现有的防空武器，来袭无人机集群通过第三层防线时被射击的概率几乎可以达到100%，但是仍有7.1%的无人机作战单元突防成功。这说明当防空武器数量满足来袭无人机集群强度时，提高武器毁伤率对于提高作战效能有很大的帮助。

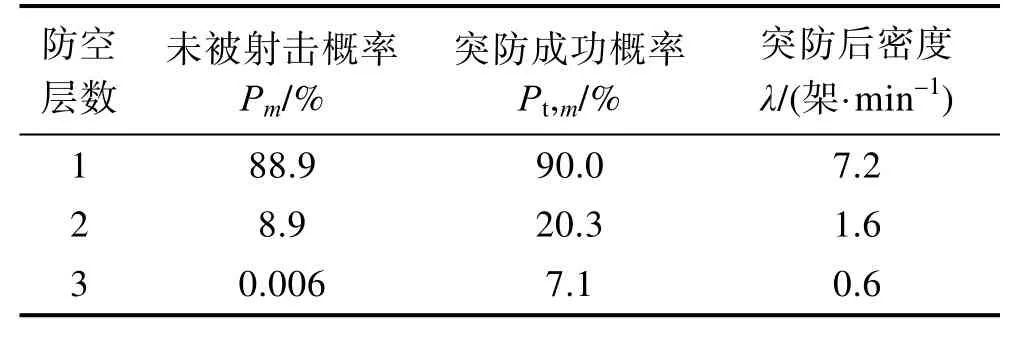
表2 各层防线防空效能计算结果 Tab.2 Calculation results of air defense effectiveness of each layer of defense line

3.2 结果分析与优化

为满足多层次、立体化拦截的要求，鉴于第1层防线的远程防空武器数量为1，因此不作为变量进行分析。研究每层防线防空武器的数量问题就变成了第2、3层防线防空武器的数量问题（下同），在满足无人机集群突防概率不大于0.1的情况下，使得第2、3层防线的防空武器数量组合最小，从而得到防空武器部署优化模型为：

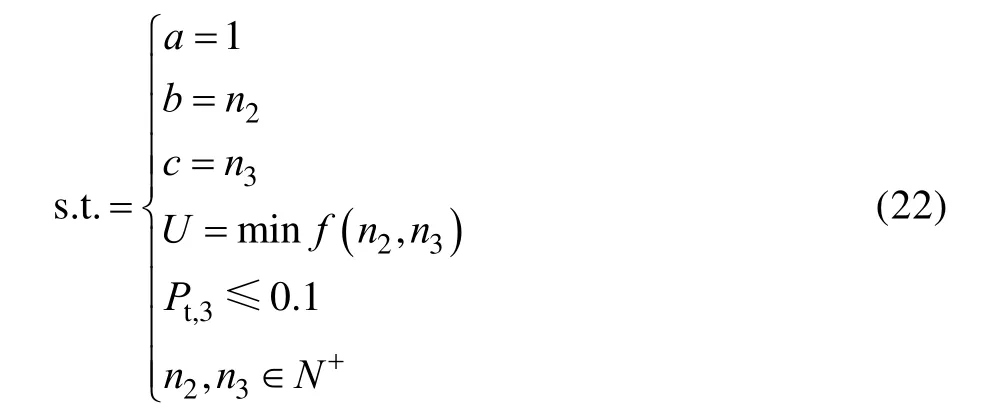
基于上述模型，将第2、3层防线的中程、近程防空武器数量作为变量，与2.2节和2.3节所建立模型相结合，得到中程、近程防空武器数量与无人机集群最终突防概率的关系，如图2所示。

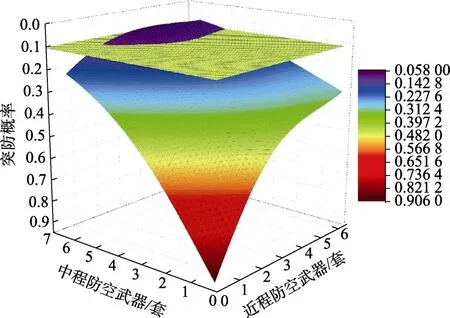
图2 防空武器数量–目标突防概率关系 Fig.2 Relationship between number of air defense weapons and target penetration probability

从图2中可以看到，随着中程、近程防空武器数量的增加，无人机集群突防概率呈现出“前快后慢”的变化趋势。在云图中突防概率≤0.4的区域，随着武器数量的增加，其坡度的变化越来越缓慢，说明在这个区域逐渐出现了“饱和式攻击”。因此，在进行防空武器兵力部署时，不一定要追求数量上的越多越好，数量过多反而会加大兵力负担，降低效费比，造成浪费。

将突防概率0.1作为临界值，把=0.1的平面作为临界面与突防概率模型相交，其交线定义为“临界线”。可以得到，在“临界线”两侧分别为满足防御要求的武器数量和不满足防御要求的武器数量。为了更形象表达，将图2的相交平面进行投影，然后将投影区域数字化和网格化，进而得到了在指定突防概率条件下每层防线的武器数量与防御效果，如图3所示。将“临界线”两侧分别定义为危险区和安全区，通过图3可以直观地看到中程、近程防空武器数量组合所对应的防御效果。在红色安全区，防空武器数量可以任意搭配，均能够保证不大于0.1的无人机集群突防概率，越靠近“安全线”，防空武器的总数量越少，即“安全线”内侧的武器组合总数量大于外侧的武器组合总数量。在“安全线”内侧的武器组合中，“安全线”转折处的武器组合总数量最小且相同。在满足尽可能用最少武器总数量达到指定防空效果的前提下，将该处的区域定义为“理想区”，显然，本文有2个“理想区”可供选择。

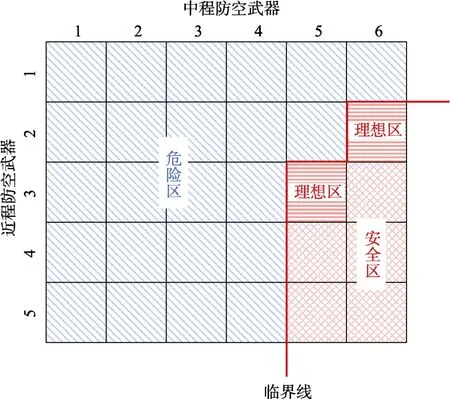
图3 武器数量与防御效果对照 Fig.3 Comparison chart of weapon quantity and defense effect

根据3.2.1节结果可知，虽然可能出现多组处在“理想区”的防空武器组合，但其总体防御成本必然存在差异，因此当防空系统中武器总数量相同时，经济效益将是决定武器组合“最优解”的重要因素。对于层防线的防空系统，其总体防御成本可以利用数学中期望值的概念进行求解。将单个来袭目标在每层防线中的被射击概率和单次拦截成本乘积的总和定义为防空系统对单个来袭目标防御成本的期望值，再把期望值与目标总数相乘，即可得到总体防御成本，见表3。

表3 单个来袭目标进入第m层的防御成本 Tab.3 Defense cost of a single incoming target entering layer m

防空系统对单个来袭目标防御成本的期望值如式（23）所示：

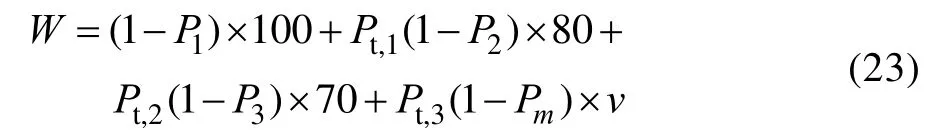
由于无人机集群总数为定值，式（23）所求的对单个来袭目标防御成本即可代替总体防御成本，对本文部署优化结果无影响。根据第2节所建立模型，结合前文已经求得的“安全区”和“理想区”结果，在此基础上将拦截成本考虑其中，得到在满足指定突防概率条件下，防空武器总数量最小，防御成本最低的最优解。经过求解，得到在满足不大于0.1的突防概率条件下，远程、中程和近程防空武器分别为1、5、3套的数量组合对单个来袭目标防御成本达到最低，为89.2万元，是本文“理想区”内的最优解。

4 结论

立足我国当前军事形势，基于排队论模型，对3层防线构成的防空系统层层建模，描述无人机集群来袭过程，得到了本文案例中无人机集群未被射击概率、突防成功概率和突防后密度等指标的结果。

1）在满足指定突防概率条件下，将防空武器数量作为优化目标，建立防空武器部署优化模型，发现随着中程、近程防空武器数量的增加，无人机集群突防概率呈现出“前快后慢”的变化趋势。当防空武器数量满足来袭无人机集群强度时，提高防空武器毁伤率对于提高作战效能有很大的帮助。

2）提出“安全线”和“理想区”模型对防空武器组合进行划分，直观便捷地得到了能够满足指定突防概率和最小数量的武器组合，具有较强的工程价值。

3）在最小数量的武器组合基础上，将防御成本作为优化目标，利用期望值概念计算防空系统对单个来袭目标的防御成本，得到了当远程、中程和近程防空武器分别为1、5、3套时，总体防御成本最低，对单个来袭目标的防御成本为89.2万元，是“理想区”内的“最优解”。