基于国内棉花产量序列的实证分析

乔　乔

基于国内棉花产量序列的实证分析

乔乔

（内蒙古财经大学内蒙古呼和浩特010070）

近年来，全球棉花市场呈现出供小于求的局面。为探究国内棉花产量时间序列变化规律，揭示棉花产量序列的性质，分析棉花产量大幅变化带来的影响，文章通过运用Stata软件进行时间序列分析及模型拟合预测，得出结论：由于近5年～10年全球棉花市场的变化，以及国内产业结构调整，棉花整体产量小幅下降，且由于棉花的多功能性及多需求性，供不应求的局面在一定程度上会持续。并基于国内棉花生产存在的问题，对进一步保障国内棉花产量及市场预测提出了合理化建议。

棉花；产量；Stata软件；时间序列；时序分析

近年来，棉花产量持续小幅下降，全球棉花贸易局势渐变。如何根据国内棉花产量时间序列数据及面板数据，与时俱进地为“革新棉花相关产业政策，推动新时代棉花高质量发展”提供可参考性分析及建议，已成为国内诸多相关学者亟须解决的关键课题。

为推进国内棉花产量序列相关分析研究，本文延续朱爱孔等（2021）学者的研究方向[1]，参考王丽娜等（2004）学者的模型研究思路[2]，根据近40年国内棉花产量时间序列数据，运用描述性统计分析及模型分析方法，探究国内棉花产量时间序列变化规律，进而预测未来棉花市场变化。

1 研究背景及意义

1.1 研究背景

自2021年3月起，棉花贸易整体局面持续变化。伴随着棉花产量的持续下降，棉花贸易整体局面日渐严峻，国内相关产业首当其冲。

不难发现，目前棉花竞争格局较为稳定，而我国作为全球棉花出口大国之一，自2017年棉花产量小幅下降，种植面积减少，早已呈现供难应于求的局面。加上棉花贸易整体局面的变化，棉花产量将会持续变化。

1.2 研究意义

为厘清国内棉花产量时间序列变化规律，揭示棉花产量序列的性质，本文采用时间序列分析、建模及预测进行拟合，通过对结果进行量化分析，发掘现存问题，并提出一定的可参考性建议。

2 指标选取与数据搜集

基于棉花整体贸易的严峻局势，且棉花作为重要的农作物之一，其果实、果壳等均可利用，其年产量具有很好的现实分析意义与经济分析意义。本文选取1978年—2021年国内棉花产量作为分析指标，通过在EPSDATA数据库中选择既定指标及指标数据，进行后续数据分析及建模。

3 实验过程

3.1 平稳性检验

将1978年—2021年棉花产量序列数据导入Stata软件数据框中，通过图检验法及单位根ADF检验方法检验序列的平稳性，输出结果如下。

3.1.1 图检验法（初步检验）

通过对时序图（如图1）初步判断，得出该序列跨度为44年，无缺失值；棉花产量序列存在线性趋势，即原序列不平稳。周期长度并不固定，不符合季节效应，更无明显曲线趋势。

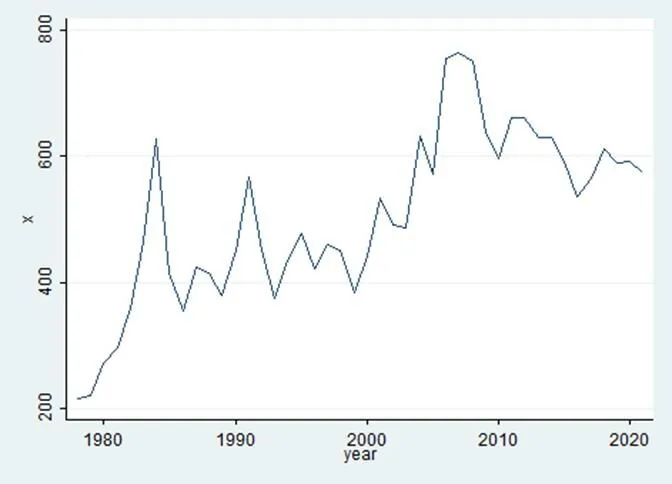
图1　（原序列）时序图

由于原序列图初步判断不平稳，则需对原序列进行差分，先尝试一阶差分。将原序列差分后记为序列{t}，并对差分后序列再做时序图检验，结果如图2所示。

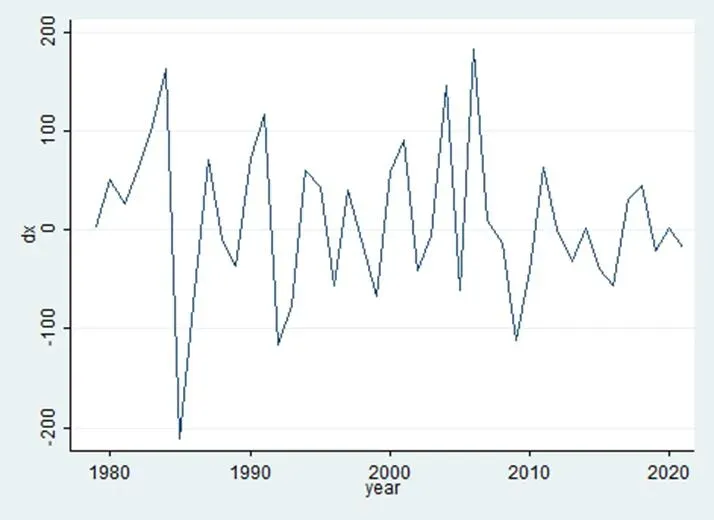
图2　一阶差分后时序图

由图2可知，根据平稳时间序列均值、方差为常数的性质，差分后序列{t}的时序图始终在一个常数值附近随机波动，且波动范围有界，无明显趋势或周期性特征，故初步判断该序列{t}平稳。

3.1.2 单位根ADF检验

由于时序图无法准确判定序列的平稳性，为了进一步确定其平稳性，对差分后序列{t}做单位根ADF检验及结果如下：

（1）Step 1：建立假设——

0：差分后序列{t}非平稳。

1：差分后序列{t}平稳。

（3）Step3：计算值进行判定：

当＜=0.05时，拒绝原假设，认为差分后序列{t}显著平稳；

当＞=0.05时，接受原假设，认为差分后序列{t}显著非平稳。

经过单位根ADF检验，得到检验统计量=-6.992，且由于ADF统计量的值小于显著性水平=0.05，所以拒绝原假设，即差分后序列t是平稳序列。

3.2 纯随机性检验

在差分后序列通过平稳性检验，认定为平稳序列后，对平稳差分后序列进行纯随机性检验及结果如下：

（1）Step 1：假设条件——

0：平稳序列{t}为纯随机序列。

1：平稳序列{t}为非纯随机序列。

（2）Step 2：构造检验统计量/。

（3）Step 3：计算值进行判定——

当部分延迟阶数下，检验统计量的＜时，则认为拒绝原假设，该序列为非白噪声序列，序列之间有相关关系，有研究价值（允许部分值大于的情况出现）。

当全部延迟阶数下，检验统计量的＞时，则认为无法拒绝原假设，该序列为纯随机序列，序列之间无相关性，无研究价值。

经过纯随机性检验，得出大部分值均小于给定的显著性水平=0.05，从而拒绝纯随机序列的原假设，认为该序列为非纯随机序列，即该序列蕴含相关信息，有分析研究价值，可以建立模型拟合该序列中信息的规律。

3.3 模型定阶

针对平稳非纯随机序列{t}，通过求出观察值序列的样本自相关系数ACF与样本偏自相关系数PAC的值，根据ACF及PAC的性质，选择阶数适当的ARIMA（,,）模型。

3.3.1 辅助判断标准——2倍标准差范围

如果样本自相关系数或偏自相关系数在最初的阶明显大于2倍标准差范围，而后几乎95％的自相关系数都落在2倍标准差的范围以内，而且通常由非零自相关系数衰减为小值波动的过程非常突然。这时，通常视为（偏）自相关系数截尾，截尾阶数为。

如果有超过5%的样本自相关系数落入2倍标准差范围之外，或者由显著非零的相关系数衰减为小值波动的过程比较缓慢或者非常连续，这时，通常视为不截尾。

3.3.2 模型定阶

通过计算各阶ACF值得出，自相关系数是以一种有规律的方式，按指数函数轨迹衰减的。这说明自相关系数衰减到零不是一个突然截尾的过程，而是一个连续渐变的过程，这时自相关系数表现为拖尾。

通过计算各阶PAC值得出，除了2阶偏自相关系数在2倍标准差范围之外，其他阶数的偏自相关系数都在2倍标准差范围内，这时偏自相关系数可判断为拖尾或2阶截尾。

根据自相关系数拖尾，偏自相关系数1阶截尾的属性，可以初步确定对原序列拟合ARIMA(1,1,1)模型、ARIMA(2,1,0)模型以及疏系数ARIMA（(2),1,0）模型。

3.4 参数估计

针对差分后序列初步确定的拟合模型进行参数估计，并使用最小二乘法确定模型口径。

3.4.1 模型1

对原序列拟合ARIMA(1,1,1)模型等价于对差分后序列拟合ARIMA(1,0,1)，拟合模型及输出结果如下：

3.4.2 模型2

对原序列拟合ARIMA(2,1,0)模型等价于对差分后序列拟合ARIMA(2,0,0)，拟合模型及输出结果如下：

3.4.3 模型3

对原序列拟合疏系数ARIMA（(2),1,0）模型，拟合模型及输出结果如下：

3.5 模型检验

3.5.1 参数显著性检验

（1）检验步骤

①Step 1：提出假设——

0：参数显著为零，即参数不显著。

1：参数显著非零，即参数显著。

②Step 2：构造检验统计量。

③Step 3：给定显著性水平，计算值进行判断——

如果＜=0.05，拒绝0，认为参数显著；

如果＞=0.05，不拒绝0，认为参数不显著。

（2）三个模型分别进行参数显著性检验

①模型1：对差分后序列拟合ARIMA(1,0,1)模型

通过拟合ARIMA（1,0,1）模型，maL1.的=1.000，在=0.1水平下参数不显著。

②模型2：对差分后序列拟合ARIMA(2,0,0)模型

通过拟合ARIMA（2,0,0）模型，arL1.的=0.335，在=0.1水平下参数不显著。

③模型3：对差分后序列拟合疏系数ARIMA（(2),0,0）模型

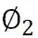
3.5.2 模型显著性检验

（1）检验步骤

①Step 1：提出假设——

0：残差序列为白噪声序列。

1：残差序列为非白噪声序列。

②Step2：构造统计量。

③Step3：给定显著性水平，计算值进行判断——

在任意延迟阶数下，如果存在任意＜，则拒绝0，认为残差序列为非白噪声序列，信息提取不充分，拟合模型不显著，为无效模型。

在所有延迟阶数下，如果所有＞，则不能拒绝0，认为残差为白噪声序列，提取信息充分，拟合模型显著有效。

（2）对三个模型分别进行检验

①模型1：对差分后序列拟合ARIMA(1,0,1)模型

通过软件拟合得出：对于任意延迟阶数，检验统计量的值均大于显著性水平（=0.05），故在95%的概率下，不能拒绝该序列为纯随机性序列的原假设，即模型残差序列为纯随机序列。

②模型2：对差分后序列拟合ARIMA(2,0,0)模型

通过软件拟合得出：对于任意延迟阶数，检验统计量的值均大于显著性水平（=0.05），故在95%的概率下，不能拒绝该序列为纯随机性序列的原假设，即模型残差序列为纯随机序列。

③模型3：对差分后序列拟合疏系数ARIMA((2),0,0)模型

通过拟合得出：对于任意延迟阶数，检验统计量的值均大于显著性水平（=0.05），故在95%的概率下，不能拒绝该序列为纯随机性序列的原假设，即模型残差序列为纯随机序列。

3.6 模型优化

将模型1、2、3的检验结果总结如下：

模型1与模型2均未通过参数显著性检验，而模型3参数显著性检验及模型纯随机性检验均通过。模型优化是针对通过模型检验的模型进行选择，故将前两个模型舍去，选择模型3。故后续分析均针对模型3进行。

通过软件拟合，输出模型3结果：AIC=496.512 8，SBC=501.865 3。

3.7 数据预测

针对模型3——对差分后序列拟合疏系数模型进行数据预测，输出结果如图3、图4所示。

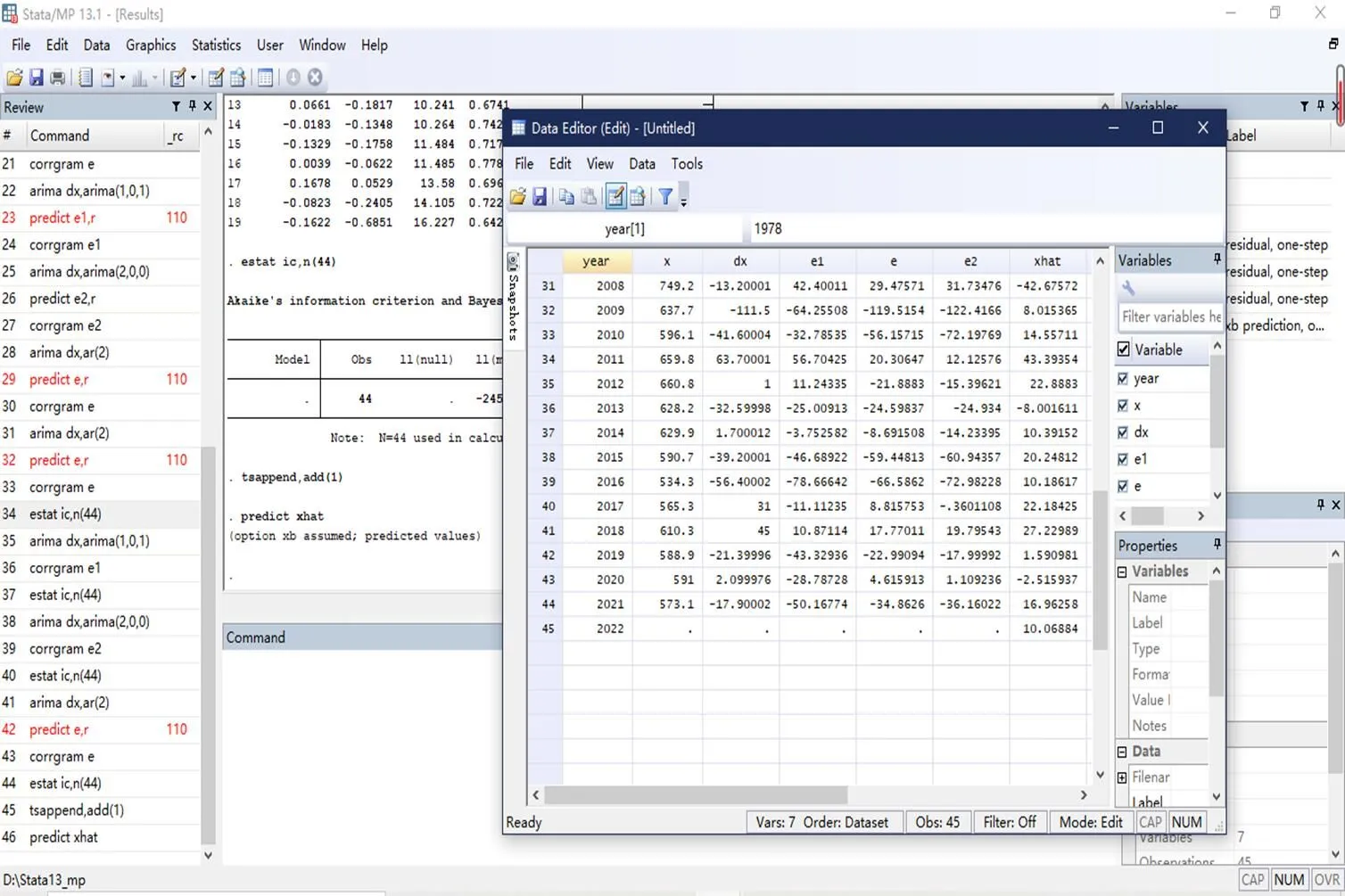
图3　数据预测图

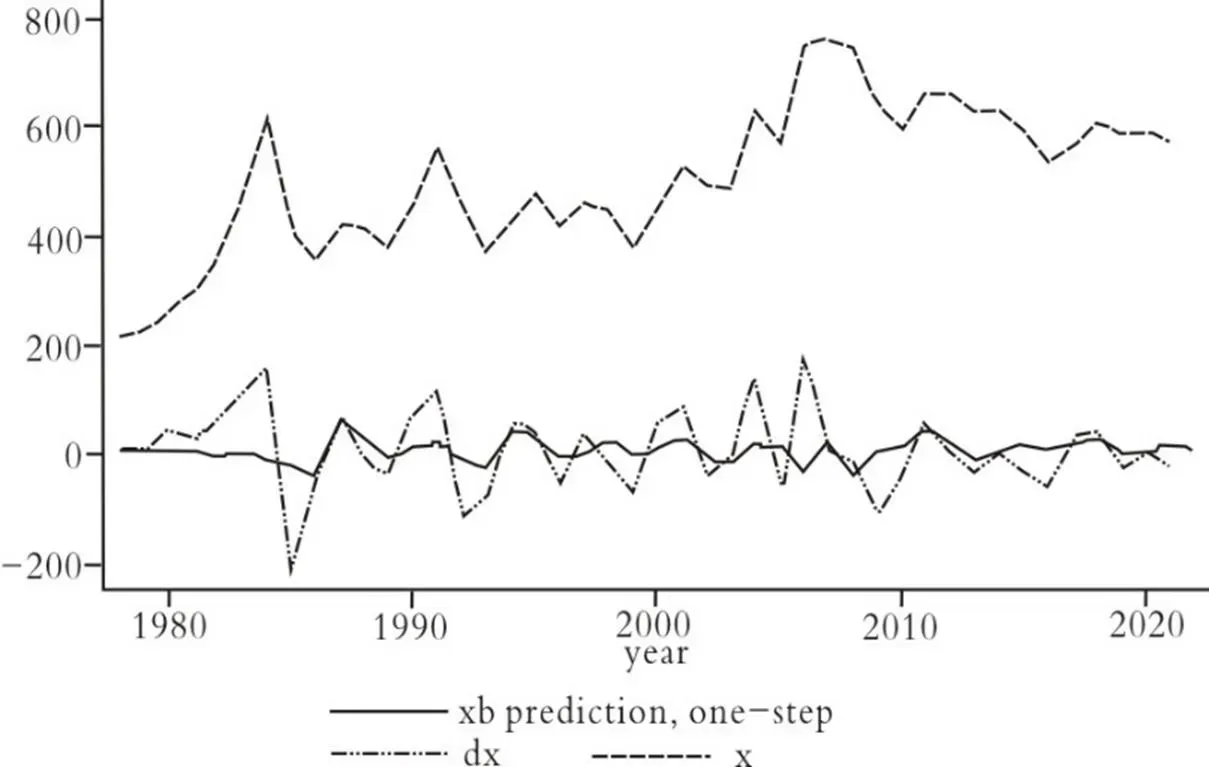
图4　最终趋势图

4 结论与建议

4.1 基于国内棉花产量序列分析的结论

由图3可知，与真实数据（差分后数据）相比：在1987年之前序列预测存在很大的差异性；在1990年—2000年、2010年—2020年序列预测较为准确。这反映出国内外不断调整棉花种植等的相关政策对棉花产量预测有直接影响，会导致某一阶段预测的偏差。我国应密切关注全球贸易局势，进而指导国内生产。整体看来，序列数据预测拟合较好，即可根据趋势指导未来国内棉花生产和市场风险评估。

由图4可知，差分后数据拟合预测曲线（曲线whitexhat）与差分后原序列数据拟合曲线（曲线blackdx）整体趋势一致，反映出差分得当；序列数据预测曲线在2010年之后整体特征大体符合原序列及差分后序列波动。

最终得出结论：由于近5年～10年全球棉花市场的变化，以及国内产业结构调整，棉花整体产量小幅下降，且由于棉花的多功能性及多需求性，供不应求的局面在一定程度上会持续。加之棉花整体贸易局势的动荡，如何保证国内棉花储备率，成为现阶段亟须解决的问题。

4.2 基于国内棉花产量序列分析的意见及建议

针对以上问题，加之国内外棉花整体产量持续小幅下降的现状，我国应在棉花种植及采摘环节提高自动化普及率，提升我国农业生产效率；同时密切关注全球贸易局势，进而调整国内棉花生产过程，一定程度上缓冲非可控因素对国内棉花产业的冲击。

通过序列拟合及后续影响因素分析，做好未来棉花市场的风险预测，应对棉花市场供不应求的持续局面，让国内棉花坚持向优质高效生产的方向发展。

5 结语

本文基于棉花贸易局面大幅动荡，分析国内棉花产量趋势，得出结论：国内外棉花产量整体小幅下降的局面将会持续，且由于我国为提升综合国力进而调整国内产业结构，国内棉花产量将受到更多非可控因素的共同影响。密切关注全球经济局势，灵活调整国内棉花生产，努力提高农业高效自动化普及率，成为当前相关人员亟须面对并解决的事情；并通过预测未来棉花产量趋势及市场潜在风险，促进国内棉花产业高质量发展。

[1]朱爱孔,何芳,韩明悦.需求侧管理下的我国新疆棉纺织产业高质量发展路径探索[J].中国棉花加工,2021(4):16-19.

[2]王丽娜,肖冬荣.基于ARMA模型的经济非平稳时间序列的预测分析[J].武汉理工大学学报(交通科学与工程版),2004(1):133-136.

10.3969/j.issn.2095-1205.2022.05.33

F326.1

A

2095-1205(2022)05-100-04