基于多秘密共享的电子文件元数据区块链存储研究

孙尧 吴妍

（1.济宁职业技术学院 山东省济宁市 272000 2.济宁技师学院 山东省济宁市 272000）

元数据是电子文件管理中的核心数据，ISO15489文件管理国际标准将其定义为“描述文件的背景、内容、结构及其整个管理过程的数据”。随着新一代信息技术的发展，电子货币的兴起，比特币的核心技术区块链，得到了世界各国的学者和政要的广泛关注。2018年5月和2019年10月习近平总书记分别在中国科学院两院大会和中共中央政治局集体学习会上强调要探索“区块链+”在民生领域的运用。全国上下开展区块链技术学习高潮，刘越男等从技术和管理的双向视角出发，对区块链如何在文件档案管理部门应用做了详细的阐述。国外，加拿大不列颠哥伦比亚大学（UBC）Lemieux的相关研究一枝独秀。她根据文献研究和访谈调研，得出区块链技术本质上是一种电子文件管理技术的结论。由于区块链技术采用了密码学和信息安全技术，利用区块链技术对电子文件的元数据进行存储，保障了元数据的安全性，完整性。区块链通过其自身共识机制来保证系统去中心化，从而使得元数据在存储过程中无需考虑第三方的可靠性问题。同时区块链利用链上的时间戳和操作行为记录来保障元数据的可追溯性和防篡改性。这也使得存储在区块链上的元数据带有了时空背景和操作行为记录背景，扩展了元数据的外延。

1 传统区块链技术存储

在区块链数据存储过程中每隔一段时间会产生一个新数据区块，它是区块链存储数据的实体。数据区块分为区块体和区块头，区块体是利用Merkle 哈希树结构进行对数据的存储；区块头部是用来存储数据区块的基本信息，是维护数据区块和工作量证明的基础，区块头部包含了Merkle树根、版本号、时间戳、随机数、区块哈希值等信息。并通过的共识机制选出一个节点，该节点拥有记录本轮行为数据的权利，通常称为记账节点。记账节点会将本轮需要记录的交易数据，打包在数据区块中，然后链接到区块链中，并给全网广播本轮打包的数据，其他共识节点通过验证后，同步更新存储数据，达成数据共识。所以每个节点存储的每一数据区块都是同一轮的同一个数据副本。

通过上述对传统区块链技术的存储过程分析可得出，由于整个区块链中每个节点上的数据区块采用保存同一轮同一个交易副本策略，因此在区块链中包含了大量的重复数据，我们调研一个区块链技术的一个应用案例——比特币系统，截止到 2018 年 10 月 18 日，比特币中共产生了546349个区块，每个区块数据量为 996.2KB，因此比特币一个完整链的数据量大小为186.9 GB。随着电子货币市场的火爆和业务增加，现如今比特币全节点（保存完整的区块链信息节点）的数量已有 1 万多个，可计算出全节点需要的存储容量为 2000 TB ，但仅仅存储了有效数据 大约200 GB 。对于区块链中的一个节点目前需要上百GB容量进行存储链上数据；对于整个区块链网络，所需存储量与区块链需要的有效存储量之间相差巨大，使得存储空间被极大地消耗和浪费。当区块链技术应用于在存储元数据场景中时，由于元数据的数据量大，会导致现有的区块链技术在数据存储代价过大的问题。势必会让单个节点和整个区块链系统难以承担，这也是目前区块链技术难以在数据量较大的元数据存储领域应用的主要原因之一。

2 改进存储算法的文献综述

为了解决区块链存储问题，很多学者针对传统区块链存储技术提出了自己的改进策略和技术框架。Dai等提出一种基于网络编码分布式存储策略( Network Coded Distributed Storage)，利用网络编码对交易数据进行分片处理，然后采用分布式存储方法，将分片数据存储在不同的区块链节点上，从而构建一种低存储代价的区块链框架。Dennis等提出了一种基于时间的数据区块滚动策略，在区块链安全前提下有效的解决业务量增大区块链存储瓶颈问题，建立一种具有可伸缩性的区块链存储框架。Dorr等利用过时交易数据合并或移除的策略，建立了记忆优化弹性区块链框架(MOFBC)。Raman 等第一次提出了一种基于秘密共享策略的分布式存储区块链框架（DSB），采用了将交易数据加密分片和分布存储到不同的区块链节点上的方式，有效的降级了区块链的存储代价。Kim等利用本地秘密共享策略（LSS），对DSB框架进行了改进，有效避免了由部分节点的丢失，造成交易数据的无法重构问题。

3 基于多秘密共享策略下的区块链存储模型设计

针对于电子文件保管领域中元数据的复杂和多样，本文提出采用多秘密共享策略来来对区块链存储模型进行设计。基于该策略对传统区块链存储模型进行改进。该存储过程分为两部分：

（1）基于多秘密共享策略下的元数据在区块链中分片过程；

（2）分片数据的重构元数据过程。并给出改进后的存储模型过程描述、算法描述。

3.1 基于多秘密共享策略简述

秘密共享技术是信息安全和现代密码技术一个重要专业分支，该技术最早应用对秘钥的保护，现在广泛应用于P2P网络中，如无线传感器网络（WSN）。而多秘密共享策略是由单秘密共享策略发展而来，1979年Shamir等人基于拉格朗日插值方程的数学原理，发明了Sharmir门限秘密共享算法，其主要内容为：将一个秘密S分为n份，只需要其中k份就可以重新还原秘密S，如果小于k份，就不能还原秘密S。其中K值就是Sharmir算法的门限值。它有两个阶段构成

（1）秘密分解阶段，构建n阶多项式其数学形式为公式1，利用f(x)将秘密S分解为n份秘密[1,f(1)],[2,f(2)]……[n,f(n)]。

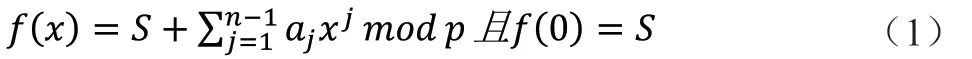
（2）秘密重构阶段，利用拉格朗日差值原理，将k份秘密带入数学公式2，算出f(x)表达式，从而得出S=f(0)

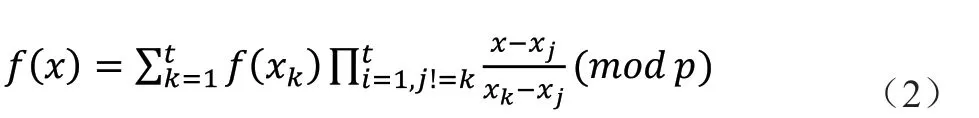
Carlo Blundo, Alfred De Santis等人第一次提出了多秘密共享策略的方案，此方案是基于Shamir秘密共享策略发展而来，将一次对一个信息进行分解共享，改进为一次对多个信息进行分解共享。多秘密共享策略的核心概念为：n个参与者可以对l个不同秘密{S,S,…,S∈K|(K为秘密空间),l∈N}根据l个不同的访问结构{Γ,Γ,…,Γ}进行秘密共享。

多秘密共享方案的流程分为三个阶段，初始化过程，多秘密分片阶段，多秘密分片重组阶段，下面对这三个方面进行形式化描述：

（1）初始化阶段：定义一个参与者集合P={P,P,…,P}和一个访问结构集合{Γ,Γ,…,Γ|l∈N}输出公开参数pms，形式化公式为3：

（2）多秘密分片阶段：将初始化阶段产生的公开参数pms和秘密集合S={S,S,…,S}作为输入端，通过多项式f(x)分解后，得到参与者的秘密共享份额集合{i,sh}和一组相关公开参数out，形式化公式为4：

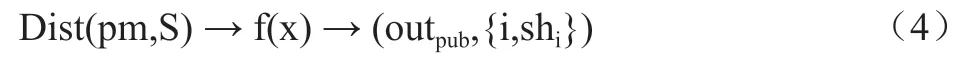
（3）秘密分片重组阶段：输入公开参数pms和out、分享的秘密类型值j∈{1,2,…l}、一组秘密份额集合{i,sh}，输出对应的秘密S，形式化公式5：

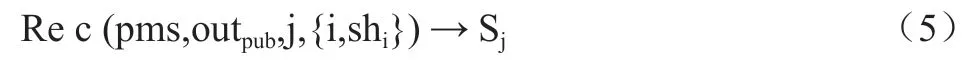
3.2 基于多秘密共享策略下的元数据在区块链中分片过程模型描述

（1）设电子文件的元数据类型个数为m，其数学集合形式为P={P,P,…P}，其中P代表第m类行为数据类型。

（2）设节点G为获取了记账权的记账节点；本轮记录P类型元数据为S。

（3）由记账节点G，构建t阶多项式f(x)，且令f(0)=S。

（4）由记账节点G，通过随机函数random(n)生产n个值互不相同的随机数sh∈Z，作为本轮对应的n个共识节点{x,x…x}的元数据的份额。

（5）对于第j(j∈1,2,…,m)类型的元数据，记账节点G进行n次公式6和公式7计算，其中公式5中的H(a,b)函数为单向哈希函数，i=1,2,…n

而基于多秘密共享策略下，将一轮根据不同的元数据类型分解为n个数据分片，散列存储在n个共识节点的数据区块中，不再是传统数据区块中存储相同的数据副本，因此需要对传统数据区块的数据结构进行改进，来适应多秘密共享策略下的数据存储需要。

新策略下的区块的数据结构模型是在传统区块的数据结构模型基础上进行的改进，主要是针对数据区块中用于数据存储部分的区块体进行改造。改进后的区块体模型中包括六个单元：记账权节点地址，元数据类型，门限参数(k,n)，数据份额，元数据哈希值，分配数据的ID号，参数(k,n)。其中记账权节点地址，元数据类型，门限参数(k,n)，元数据哈希值，这四个单元在本轮数据共识过程中属于副本数据，它们对于每个节点来说数据是相同的。

在传统的数据区块中Merkle树的叶子节点存储的是同一元数据副本，保障Merkle树根值和区块头部的数据不变，从而保障了工作量证明基础一致性。为了保持传统区块链中数据区块这一特性，在改进的区块数据结构模型中，将记账权节点地址，元数据类型，门限参数(k,n)这四个副本数据单元作为叶子节点链接到Merkle树上，其他三个单元没有链接到Merkle树中。这样保障了每个节点中Merkle树根值和区块头部的数据不变，从而不影响改进后区块链中每个节点工作量证明，分片过程流程如图1所示，元数据分解和分发如表1所示。

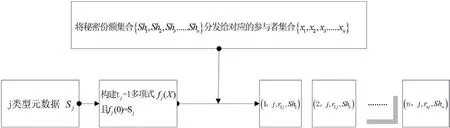
图1：元数据的分片过程流程图

表1：元数据分解和分发算法

3.3 元数据重构过程描述

在基于多秘密共享策略下的区块链存储模型中，当用户对元数据进行查询时，需要对分布式存储的分片数据进行重构还原元数据，重构过程分为两个步骤：分片数据的提取、分片数据的重组。分片提取过程模型描述：

（1）输入为要读取区块信息的位置索引 index 和行为数据类型，共识节点根据 index 值和元数据类型，查看自己区块链上对应的区块；

（2）获取该区块上记录的分发节点地址、门限参数(k,n)等信息；

（3）根据分发节点地址信息，依次向分发节点请求 index 数据区块的分片数据，k个节点根据公式8和公式9，计算出自身相应的T=[k,F(k)]的值，并发送给申请节点，直到申请节点获得 k 个分片数据为止。

通过分片提取后，共提取共识节k个分片数据为：

([1,F(1)],[2,F(2)],…[k,F(k)])，利用拉格朗日插值算法公式10，最后结果为公式11

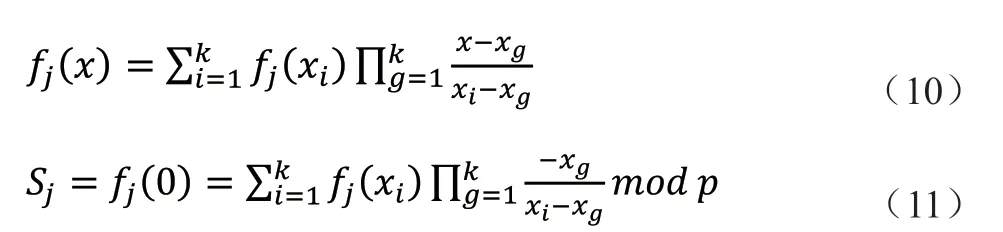
元数据重组流程如图2所示，元数据重构算法如表2所示。

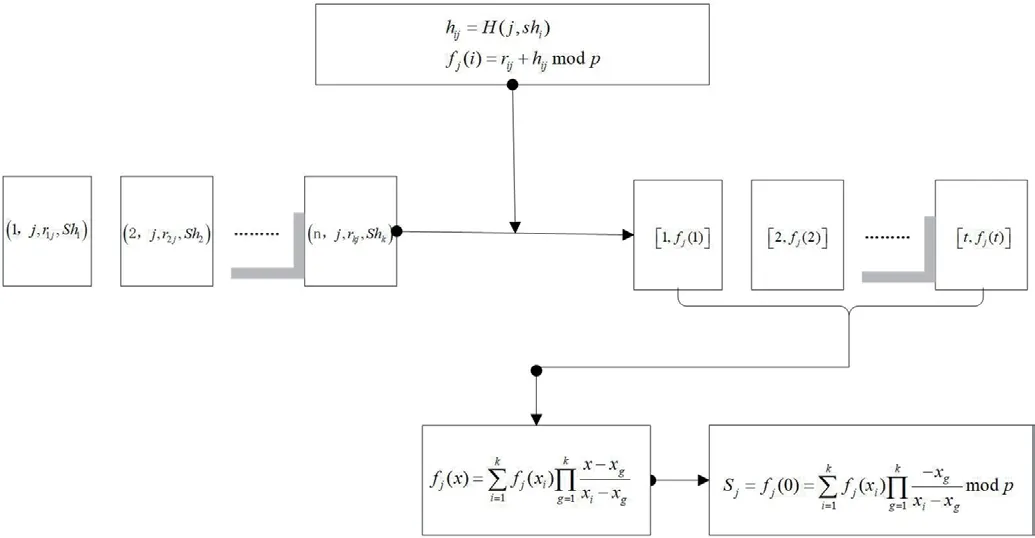
图2：元数据重组流程图

表2：元数据重构算法描述

4 模型仿真实验

4.1 存储性能数学分析

区块链本质上是一种哈希链，我们通过建立一个抽象简化的哈希链数学模型来代表区块链，从而通过该数学模型来估算出区块链的存储代价。设B为第t次交易产生的数据块，W为第t次的区块头，W的数学形式为W=(H,g(B))。其中H为前一个区块的哈希值，计算方法为H=h(W)，h( )为哈希函数，H的值存放在(t+1)的块中。g( )为哈希函数，它代表了实际的区块链中Merkle树的计算过程，g(B)代表了Merkle树的计算结果即Merkle树根值，存储于区块头部。区块链简化的哈希链数学模型，如图3所示。

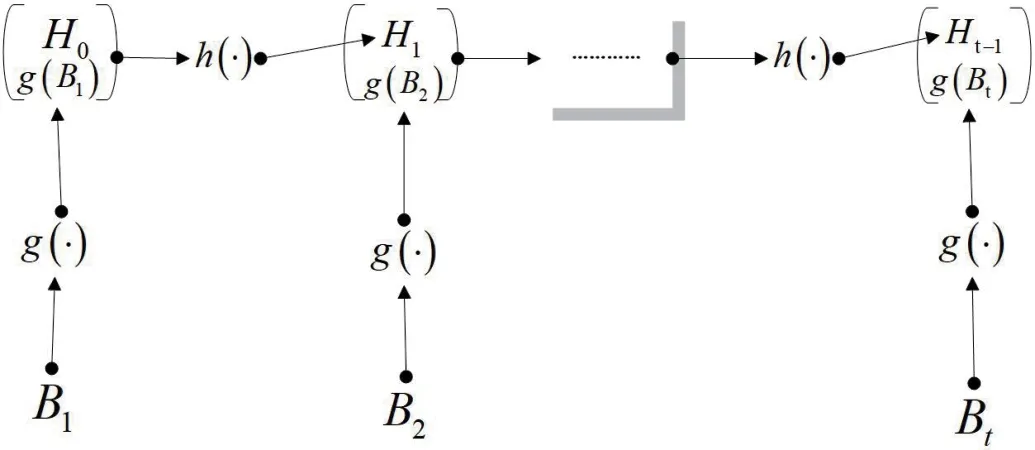
图3：哈希链数学模型

设B存储在有限域F中，即B∈F，g(B)和H存储在有限域F中，即g(B)∈F，H∈F。因此，推出在传统区块链中每一次元数据的存储代价R的计算公式为公式12，其单位为bits。

本文改进的区块链中每一次元数据的存储代价R1的计算公式为，其单位为bits。

4.1 鲁棒性数学分析

区块链中的鲁棒性是指当区块链中的节点破坏或丢失后，区块链系统所保存的数据丢失的风险程度。在传统区块链中，由于采用了链上所有节点都有一份整个区块链交易数据的副本，因此如果区块链所有的节点数为n，则传统区块链的鲁棒性为n-1即当区块链中所有节点都丢失后，才可能造成数据丢失。而基于多秘密共享策略的区块链存储模型中，对于j类型某元数据来说，如果区块链中丢失节点后，链上所剩节点数超过其设定最低重构的门限值t时，会导致该元数据无法重构，因此其鲁棒性为n-t-1。

本文通过机架式服务器运行多虚拟机来仿真区块链中多个共识节点，一个虚拟机代表一个公共节点。服务器的配置：CPU是2个Intel Xeon Silver 4114 10C 85W 2.2GHz处理器，内存32GB TruDDR4 2666 MHz(2Rx4 1.2V)RDIMM共计256G TruDDR4。

本实验的设计，利用随机函数产生一组随机数代表元数据，每10个元数据为一组，每5分钟，进行一次区块链记录，通过工作量机制，产生一个记账节点，进行对本轮10个元数据的分解和分发。每5分钟，产生一个新虚拟机代表新增一个共识节点。其中的参数规定：实验中的门限参数为 k = 5，n 值为本区块链的所有节点数，大素数 q的值为219936。

传统区块链存储效率如图4，改进实验结果如图5，可以看出随着共识节点的数目增加，传统区块链单个节点的存储量没有变化，通过多秘密共享策略改进的区块链中，随着共识节点数量的增加，单个节点的存储代价明显下降。

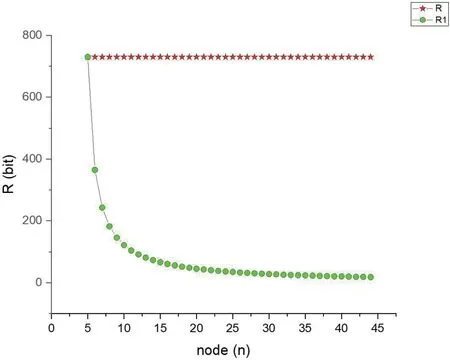
图4：传统区块链存储效率图

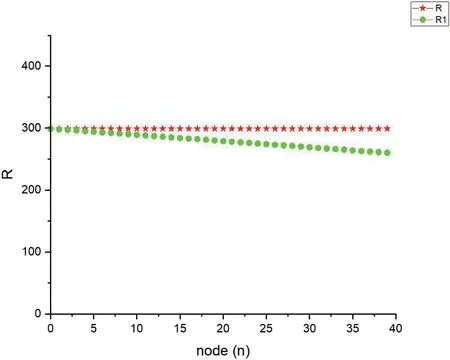
图5：改进区块链存储效率图

5 结语

根据电子文件中元数据的复杂多样性，本文创新性的提出一种多秘密共享策略下的区块链存储模型框架，并利用数学建模法给出了该存储模型的过程描述和算法描述，利用计算机仿真实验法，得出实验结果，与传统区块链存储技术对比，改进后的模型随着节点数的增加即业务量的增加，能够有效的降低区块链存储代价。本文也有一些不足之处，在多秘密共享策略中如何科学构建多项式问题以及门限参数最优值问题，需要进一步研究和改进。