基于逐位逼近Q学习的PID参数优化方法

曹文凯 洪杰 袁也 吴怀江 姜冲

（1.江苏省新能源开发股份有限公司 江苏省南京市 210018 2.南京金宁汇科技有限公司 江苏省南京市 211899）

在工业控制中，PID控制是历史最悠久，应用最广泛的控制方式。PID控制器是将比例、积分和微分环节按照一定的规律组合起来，利用系统偏差来进行控制的一种方法。PID控制器虽然具有结构简单、鲁棒性强、控制品质对被控对象变换不太敏感、适用于环境恶劣的工业现场等优点，但是PID控制系统的控制效果完全取决于控制器的三个控制参数kp，ki和kd，因此PID参数的选取成为一个很重要的研究课题。

常规的PID整定方法有理论计算法和工程整定法，理论计算法由于计算繁琐，一般在工程实践中很少应用。工程整定法是现场技术人员根据经验进行试凑。工程整定法虽然操作简单，但是这种方法控制效果的好坏过于依赖于技术人员的经验，而且比较费时，控制效果也不是很好。因此，很多学者将蚁群算法、粒子群算法，遗传算法等启发式算法用于PID参数寻优，并取得了很好的控制效果。近年来，强化学习方法成为智能系统设计的核心技术之一，被广泛应用于机器人、游戏等领域，2017年AlphaGo击败世界围棋冠军李世石和柯杰事件更是举世瞩目。强化学习算法通过“探索与利用”来对未知的环境进行探索，从而得到一段时间内的最大奖励。强化学习的这种属性在大规模的寻优问题中具有天然优势，因此很多学者也把强化学习用在路径规划和组合优化问题中，文献将强化学习中的q学习算法用于土石方的调配问题，文献等将强化学习方法应用于机器人路径规划问题。本文将强化学习中的Q-学习算法引入到PID参数优化问题中进行研究，提出了一种适应于Q-学习算法的PID参数自整定方法，仿真结果表明，该方法具有很好的控制效果。

1 强化学习和Q-学习算法

强化学习是从动物行为学以及自适应控制等理论发展而来的一种交互式学习方式。强化学习通过模仿人类的学习过程，通过不断的“试错”来对环境进行探索，并在尝试过程中利用已经学到的经验来选择最佳的策略，以获得最大的奖励。强化学习的基本模式如图一所示：agent在当前时刻t，根据所处的状态s选择动作a，并且得到环境对它的反馈信号作为奖励r，环境转移到下一个状态s。强化学习的目标就是通过学习来得到一个最优策略P:s-a，从而使得整个过程中的奖励最大。

Q-学习算法是强化学习中最为经典的算法，它不需要了解模型的任何信息，是一种基于值函数的在线学习算法。Q-学习通过优化迭代计算的状态-动作对函数Q(s,a)来得到最优策略，使得长期的累积折扣奖励总和最大。值函数可以定义为式（1）。

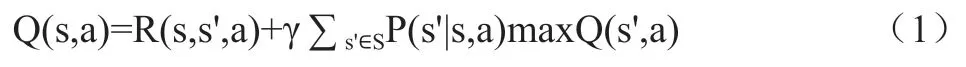
其中，α为学习率，γ为奖励衰减系数。

Q-学习算法利用Lookup-table（数组）的方法来存储状态-动作对，因此在实际应用中，其状态和动作是有限的，每一个状态-动作对会对应一个相应的Q值。在与环境进行交互时，Q-算法总是倾向于选择当前状态下Q值更高的动作，这也被称为“ε‐greedy”策略，即agent以小于ε的概率随机选择动作，以1‐ε的概率选择当前的最优动作，为了达到更好的搜索效果，可以在算法刚开始选择较大的ε值，从而可以充分探索空间中的动作，跳出局部最优，在算法后期选择较小的ε值，收敛到全局最优。Q-学习算法的伪代码如图1所示。

图1：Q-learning伪代码

Q-学习算法利用与环境交互过程中的奖励来进行学习，因此奖惩机制也是Q-学习算法的核心机制，合理的奖励函数可以得到更加好的策略，通常情况下需要根据任务的目的来设计奖励函数，并可以通过奖励塑性来加速算法收敛速度。

2 基于强化学习算法的PID参数寻优

2.1 问题建模

在强化学习问题中，agent需要根据所处的状态来对环境做出动作响应。因此，需要定义agent在k、k、k的寻优问题中的状态和动作。在文献中，研究者在利用蚁群算法进行PID控制器参数寻优的过程中，建立了蚂蚁的爬行路径图。参照蚂蚁爬行路径图设置过程，可以定义agent的状态动作空间。假设k、k、k各有五位数，整数位占一位，小数点后占四位。将kp，ki，kd按照十进制编码，组成相应的编码序列，每一个位置的动作范围均为0-9之间的整数。用XOY坐标系表示如图2所示。图中的蓝色轨迹显示了agent从原点开始，从左边运动到右边界的轨迹图。图中机器人所在的位置即是当时所处的状态，可以用机器人所在位置的坐标C(x,y)表示。图二的状态转移可以表示为：

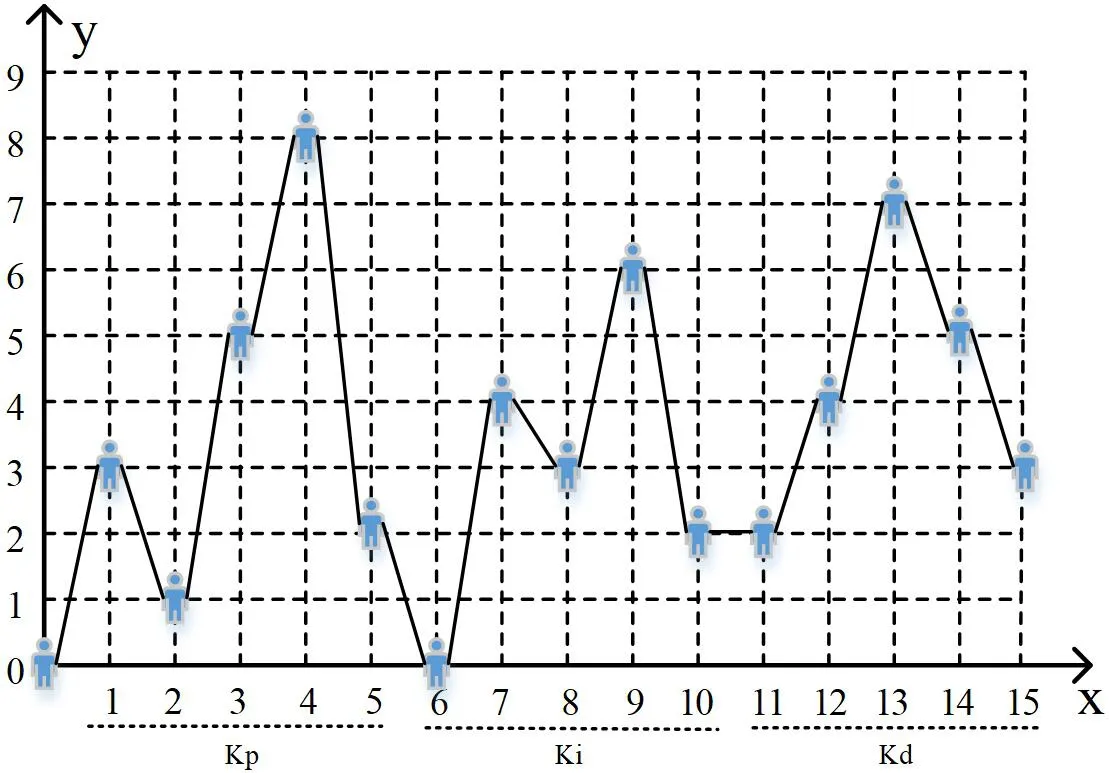
图2：agent运动轨迹图

C(1,3)→ C(2,1)→ C(3,5)→ C(4,8)→ C(5,2)→ C(6,0)→C(7,4)→ C(8,3)→ C(9,6)→ C(10,2)→ C(11,2)→ C(12,4)→C(13,7)→ C(14,5)→ C(15,3)

假设agent从原点出发，当agent从最左边的运动到最右边时，agent的运动轨迹对应着一组PID参数值：

2.2 奖励函数和探索策略设计

奖励函数的设计应该综合考虑到控制过程中的综合性能指标。在PID控制参数优化问题中，一般习惯用控制过程中超调量、上升时间、调节时间和稳态误差等指标来评价系统性能，这些指标也被称作确定性指标。确定性指标所得到的值是离散化的，不能准确反映整个控制过程的变化情况。因此，可以将时间因素引入控制品质评价指标中统筹考虑，建立误差积分指标。误差积分指标是一种综合性的指标评价标准，包括绝对误差积分、平方误差积分、时间与绝对值误差积分、时间误差积分四种。本文选用绝对误差积分指标来对控制过程性能进行评价。绝对误差积分表达式如式（2-2）所示。

绝对误差积分：

强化学习的目标是值函数的最大化。在该问题中，当agent还未到达右边界时，奖励函数可以设计为0，当agent到达右边界后，奖励函数可以设计为误差积分指标的倒数。如式（2-3）所示。

奖励函数如式（2-3）所示。

探索策略的设计要考虑到“探索和利用”平衡。探索初始化时，应该保证完全随机分配，这样可以保证迭代过程中每个状态行为对理论上都有可能被选中。探索后期，则应该更多的利用已学习到的策略。本文采用的ε‐greedy探索策略如式（3）所示，其中step表示agent的回合数，max_step表示总的回合数，随着step的增大，ε会逐渐减小，最后达到完全贪婪。

2.3 基于强化学习算法的PID参数优化步骤

（1）初始化

生成Q值表并初始化为0，设置学习率α=0.6，奖励衰变系数 γ=0.8

（2）寻优

①Agent从原点出发，根据式（3）选择每个状态的动作。

②当agent走到右边界时，按照式（2-1）分别计算kp，ki，kd的值，并通过m文件赋给PID控制器

③调用simulink模型，按照式（2-6）计算奖励函数

（3）按照式(1-1)对Q值表进行更新，step=step+1

（4）进入下一次循环，直到满足终止条件，得到最终的kp，ki，kd参数值,具体流程图3所示。

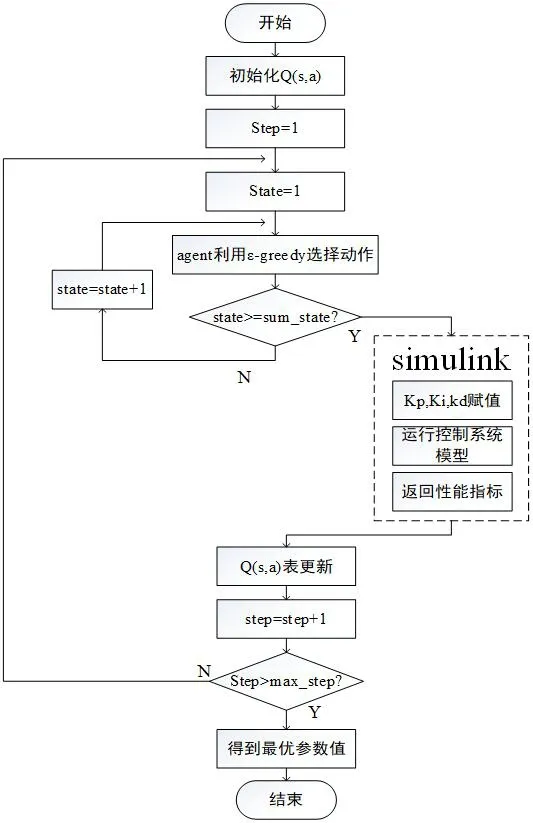
图3：程序流程图

3 仿真算例

实际工业控制中的对象一般均可用二阶系统来进行表征，因此本文选取一个二阶的广义控制对象。在matlab2017b的simulink仿真平台上搭建控制回路，如图4所示。根据控制流程图编写m文件调用simulink模型来进行PID的参数寻优。

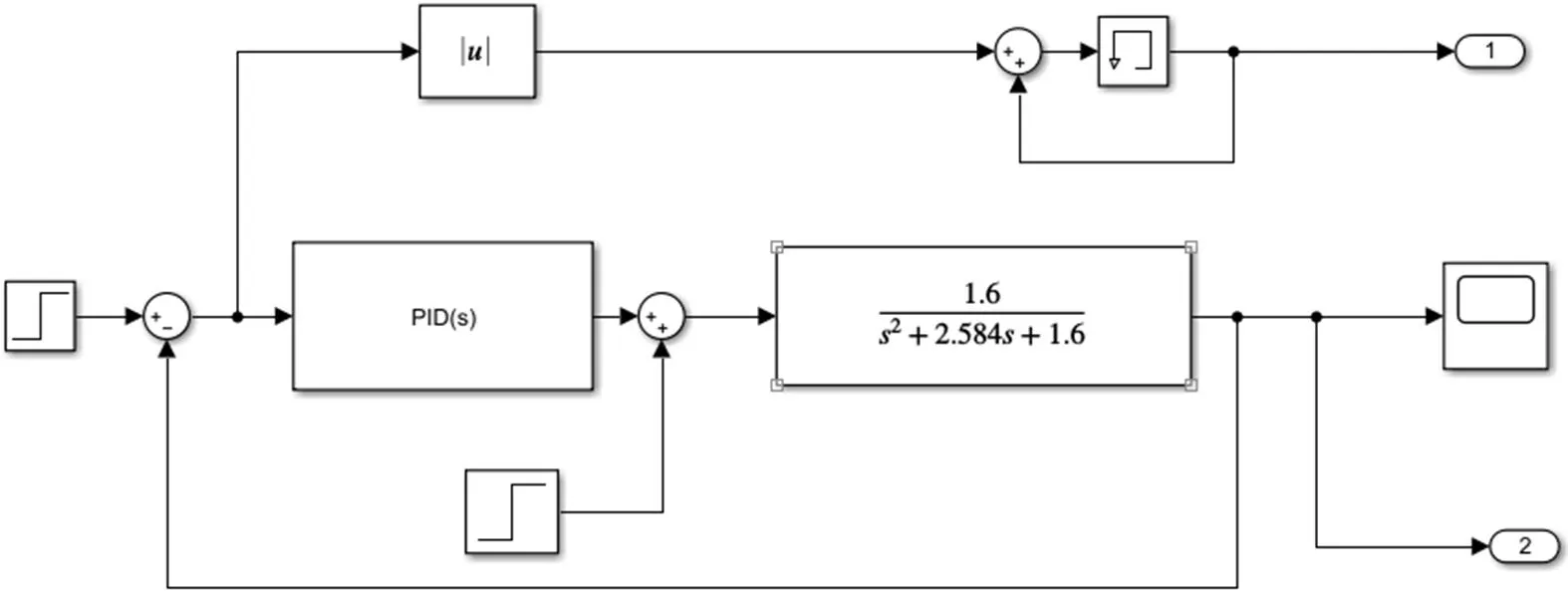
图4：PID控制模型

在matlab2017b的simulink仿真平台上搭建控制回路，如图()所示。根据控制流程图编写m文件调用simulink模型来进行PID的参数寻优。

3.1 强化学习训练结果

本文采用积分误差的倒数作为奖励函数。经过试验，当回合数为3000时，其奖励函数基本收敛。使用Q-学习算法随机进行六次不同训练过程，由于探索策略的随机探索操作，每次训练过程中的奖励值随着回合数的增长上下波动，但依然呈现上升的趋势，最终收敛于一个较大的奖励值。探索概率在每回合初始时比较大，随着回合数的增加而逐渐减小探索概率。

表1中列出六次不同训练过程中得到的寻优结果，以及每种结果所对应的超调量和调节时间（±0.03）。图5是其系统响应曲线图。

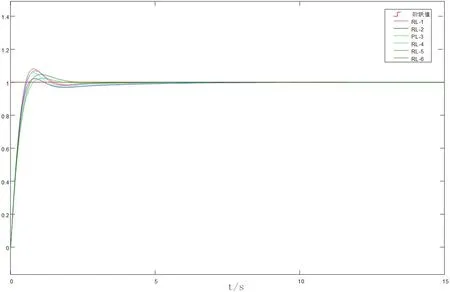
图5：Q-学习寻优系统响应曲线

表1：不同训练过程的寻优结果

由图6可以看出，RL-5的超调量最大，响应速度最快，调节时间较短。RL-3的超调量最小，但是响应速度最慢。RL-2的响应速度较快，超调量仅大于RL-3，而且调节时间也较短。总体来看利用Q学习算法寻优得到的六组控制参数控制效果都比较好，控制曲线都比较平滑，超调量也不大。

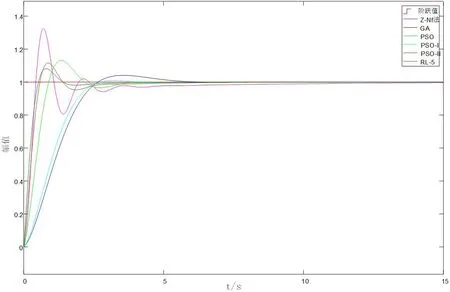
图6：不同算法系统单位阶跃响应

3.2 训练结果验证

（1）为了验证本文中提出的Q学习方法在PID参数寻优中的优越性，本文将Q-学习中RL-5的寻优结果与Z-N法，遗传算法以及粒子群算法[a][b]到的优化参数进行对比，其结果如表2所示。系统的响应曲线如图6所示。

表2：不同算法寻优结果

从仿真结果可以看出，工程整定常用的Z-N法得到的PID控制系统虽然响应最快，但是超调量也比较大，达到了32%，并且出现了强烈的波动。PSO算法的超调量和调节时间都比Z-N法要好，但是响应速度比较慢。PSO-II算法在响应速度和调节时间上均要优于PSO算法。GA算法和PSO-I算法虽然超调量很小，但是响应速度慢，调节时间长，GA算法在接近4s才到达设定值误差允许范围内。利用Q-学习算法得到的PID控制系统，不仅响应速度仅次于Z-N法，而且超调量最低，波动较小，在很短的时间内就达到了控制要求，表现出了良好的性能。

（2）在实际工业现场，控制对象的波动是不可避免的，因此改变模型的部分参数，取传递函数为3-2所示，其仿真结果如图7所示。

图7：模型失配后不同算法的系统响应曲线

从控制图像可以看出，在模型失配的情况下，GA、PSO和PSO-I控制曲线都出现了很大的波动，达到设定值所需时间到了10s左右，不再满足控制要求。Q-学习算法（RL-5）得到的优化参数控制效果仍然是最好的，具有很好的鲁棒性。

4 结论

本文针对PID参数的寻优问题，提出了一种基于Q学习的PID参数寻优方法。所作的工作主要有：

（1）通过对问题的分析，将pid参数寻优问题转化为强化学习中agent的路径寻优问题，并建立了相应的模型。

（2）通过多次随机试验，验证了Q学习算法在解决PID寻优问题中的收敛性

（3）通过与传统的工程整定方法Z-N法、遗传算法、粒子群算法的对比，充分说明了利用Q学习算法得到的参数具有更好的控制效果。

在进一步的研究中，可以在奖励函数中引入超调量、响应时间等确定性评价指标作为限制，对于不满足确定性指标评价的结果予以惩罚，加快Q学习算法的学习过程。