基于KNN算法的特征过滤预处理研究

张玉辉 常泽楠

摘  要：K最近邻算法是机器学习中一种经典的监督算法。但该算法处理数据时需要遍历所有特征，在处理高维数据时，运行效率低。针对该问题，文章采用方差过滤对数据特征进行预处理，该方法可有效降低数据特征数，提高算法运行效率。实验测试表明，经过特征预处理后的数据集，特征数有效减少，在不降低准确率的情形下，可减少30%的运行时间。

关键词：KNN;方差过滤;卡方过滤;F检验;互信息法

中图分类号：TP18      文献标识码：A文章编号：2096-4706（2022）04-0126-03

Research on Feature Filtering Preprocessing Based on KNN Algorithm

ZHANG Yuhui， CHANG Zenan

（Hunan Petrochemical Vocational Technology College， Yueyang  414021， China）

Abstract： K-Nearest Neighbors （KNN） algorithm is a classical supervision algorithm in machine learning. However， the algorithm needs to traverse all the features when processing data， and when processing high-dimensional data， the algorithm runs inefficiently. In view of this problem， variance filtering is used in this paper to preprocess data features， which can effectively reduce the number of data features and improve the efficiency of the algorithm. Experimental results show that the number of of data set can be effectively reduced after feature preprocessing， and the running time can be reduced by 30% without reducing the accuracy.

Keywords： KNN; variance filtering; chi-square filtering; F test; mutual information method

0  引  言

随着信息化建设的蓬勃发展，数据已经成为社会发展、人民生活越来越重要的一部分，对数据的分析也已成为计算机发展的一个重要方向，以数据为核心的机器学习也已成为一门重要学科，分类算法是机器学习中重点研究对象之一，包括了KNN算法、决策树算法、随机森林、逻辑回归等。其中，KNN算法具有的思想简洁、易于运用、且在分类问题的处理上有较高的准确率，已被广泛的运用于分类问题的处理上。为了能提升KNN算法效果，有大量学者对此进行了优化研究，如严晓明提出了基于类别平均距离的加权KNN分类算法，石鑫鑫等提出了融合互近邻和可信度的KNN算法，李昂提出了基于高斯函数加权的自适应KNN算法，这些学者主要的研究工作是针对KNN算法进行优化。本文从数据处理的整体出发，针对数据集中的特征进行过滤处理，采用优化数据集的方式，提升KNN算法的运行效率。本文的设计思想是采用过滤法对数据集中的特征进行优化，为此，分别对方差过滤、卡方过滤、F检验和互信息法的原理进行了研究，编写了相关的程序，并设计了一个采用卡方过滤的KNN算法的对比实验，通过对比使用卡方过滤前后的KNN算法实现效果，验证了采用过滤法后的KNN算法应用效率有了明显的提升。

1  KNN算法原理

K最近邻算法（K-Nearest Neighbors， KNN）由Cover和Hart提出，是机器学习中一种较为经典的监督算法[1]，即可用于处理分类问题，也可用于处理回归问题，其思路也比较直接，在处理分类问题时，采用少数服从多数的原则，在处理回归问题时，根据样本周围K个邻近样本的平均值或进行加权运算得到的平均值进行预测。KNN一般多用于处理分类问题，K值和距离度量是对样本进行计算时影响较大的因子。

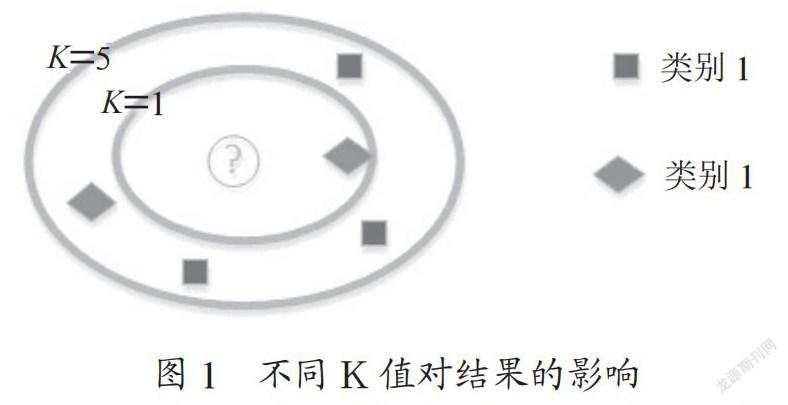
K值是指獲取特征空间中离该样本距离最近的K个值，统计这K个值中各种类别所占的个数，选出个数最多的类别作为该样式的所属类别[2]，如图1所示。此种计算方式，K值大小的设置对异常点的处理和分类的确定影响较大，当设置较大的K值时，虽然较容易排除异常点，但因包含的样本较多，模型将更简单，容易产生欠拟合的问题。当设置的K值较小时，虽然解决了欠拟合的问题，但模型将变得复杂，对异常点的排除变得困难，会带来过拟合的问题。因此在使用KNN算法中，可通过设置不同的K值，进行交叉验证并画出曲线，最终选取合适的K值。

距离度量是获取特征空间中距离最近的K个值的关键因素，关于距离的度量方法主要有：欧氏距离、马氏距离、曼哈顿距离、闵可夫斯基距离、汉明距离和切比雪夫距离等，在使用KNN算法时可根据特征空间的不同选择合适的距离度量方法。欧几里得度量是最常见的两点之间或多点之间的距离表示法[3]。在二维空间下，欧氏距离计算公式为：

ρ为点（x2，y2）与点（x1，y1）之间的欧氏距离;| X |为点（x2，y2）到原点的欧氏距离。

三维空间下，欧氏距离计算公式为：

n维空间下，欧氏距离计算公式为：

KNN算法计算时会遍历数据集中的所有特征，当数据集中的特征越多，计算所需要的时间也越长。为了缩短KNN算法的计算时长，可对特征进行预处理，过滤具有干扰性的特征和影响力为零的特征，甚至有时为了提高计算效率，在将准确率降低到可接受的前提下，过滤部分影响力较小的特征。因此，为了达到优化KNN算法，可对数据集特征进行预处理。

2  过滤法

2.1  方差过滤

方差过滤的中心思想是将特征中方差值较小的特征过滤掉，保留方差值较大的特征。因为在数据集中，某特征方差的大小决定了此特征在样本中的区别度，方差越小，区别度越小，则对样本分类计算或回归计算的影响力越小;方差越大的特征，区别度越大，对分类计算或回归计算的影响力也大。在使用方差过滤时，可设置方差过滤的阈值，当某特征的方差小于该阈值时，该特征将被过滤掉。阈值大小的设置必须与特征的取值范围相联系，当某特征的取值范围较大时，可设置较大的阈值，当某特征的取值范围较小时，则需降低阈值的大小，默认情况下，阈值设置为0，即过滤掉影响力几乎为0的特征。当数据集中某个特征为伯努利分布时，即二分类时，可采用伯努利方差过滤公式进行计算，伯努利方差计算公式为：σ=p（1-p）。在使用方差过滤预处理特征时，需根据模型计算的实际需求，在性能与精度之间找到平衡，设置合适阈值。

以下为使用方差过滤的代码：

from sklearn.feature_selection import VarianceThreshold

vt  = VarianceThreshold（threshold=val）

vt.fit（X[，Y]）  //从特征集X中学习经验方差

X_vt = vt.transform（X）   //对数据集进行过滤

如上实现过滤所有阈值小于val的特征，即过滤掉方差值小于val的特征，当不设置threshold参数时，将默认过滤阈值为0的特征。

2.2  卡方过滤

卡方过滤主要用于处理分类问题数据集中的特征，通过使用卡方方程计算每个特征与类别之间的卡方值[4]，卡方方程为：

Ai为实际频数，Ti为理论频数。

卡方值越大的特征对分类结果的影响越大，因此可通过卡方值对特征进行排序，保留卡方值较大的特征，过滤掉卡方值较小的特征，即对分类计算影响较小的特征，實现代码为：

from sklearn.feature_selection import SelectKBest

from sklearn.feature_selection import chi2

X_chi2= SelectKBest（chi2， k=100）.fit_transform（X， Y）

chi2为卡方检验类，用于计算每个非负特征与类标签之间的卡统计量，该分数可用于从特征集中选择测试卡方统计量值最高的特征，相对于类标签，该特征必须仅包含非负特征。

k=100表示获取卡方值较大的前100个特征。

2.3  F检验

F检验是由英国统计学家Ronald Aylmer Fisher提出，也称方差齐性检验、单因子方差分析或方差检验（ANOVA），F检验通过求出每个特征与标签的F统计量[5]，再根据统计量查F表，如果大于某阈值（一般选取0.05或0.01），表示此特征与标签具有较强相关性，保留该特征。如果小于某阈值，则表示此特性与标签的相关性较弱，可过滤掉此特征。F检验即可用于处理分类问题数据集中的特征，也可用于处理回归问题数据集中的特征。

使用F检验过滤分类问题特征的代码：

from sklearn.feature_selection import SelectKBest

from sklearn.feature_selection import f_classif

X_f_classif = SelectKBest（f_classif， k=100）.fit_transform（X，Y）

f_classif用于计算样本的ANOVA F值，它将返回F值和p值。如要过滤p值小于某阈值（如0.01）的特征，其实现代码：

f_value， p_value = f_classif（X，Y）

k_value = f_value.shape[0] – （p_value>0.01）.sum（）

X_fcf = SelectKBest（f_classif， k=k_value）.fit_transform（X，Y）

2.4  互信息法

互信息法通过计算每个特征与标签的互信息量值，确定每个特征与标签的相关性（线性关系或非线性关系）[6]，并且回归问题和分类问题数据集中的特征都可以使用互信息法过滤。互信息量值的计算公式为：

其中：X表示某个特性数据，Y表示标签，MI为互信息值。

Px（xi）为X的概率密度。

Py（yi）为Y的概率密度。

Px，y（x，y）为X与Y的联合分布密度。

当X与Y相关性较弱时，互信息值趋近于0，当X与Y相关性较强时，互信息值趋近于1，互信息化通过将信息值为0的特征过滤掉，达到删除无效特征的目的。

使用互信息法过滤分类问题特征的代码为：

from sklearn.feature_selection import SelectKBest

from sklearn.feature_selection import mutual_info_classif as MIC

r = MIC（X，Y）   //获取每个特征与目标之间的互信息量值，值在[0，1]之间

k_value = result.shape[0] – sum（result<=0）//獲取互信息量值大于0的特征数

X_mic = SelectKBest（MIC， k=k_value）.fit_transform（X，Y）//基于信息量实现过滤

3  实验

实验选用一组分类数据集作为实验数据，数据集包含了784个特征，42 000个样本。实验选用方差过滤对特征进行预处理，采用KNN算法结合交叉验证进行处理，通过对比过滤前后准确率与运行时间，验证特征预处理对性能的优化。

方差过滤前，运行时间与准确率如图2所示。

方差过滤后，特征数为392个，在预处理后的特征下，运行时间与准确率如图3所示。

采用方差过滤进行对比实验的过程中，在不同的数据集下，设置不同的阈值，对KNN算法的影响也会不同。当阈值设置较小时，对于方差值范围较小的数据集，过滤掉的特征将会比较多，模型的准确率会有所变化，KNN算法的运行时间会有明显地减少，算法优化效果明显;对于方差值范围较大的数据集，过滤掉的特征会比较小，模型的准确率变化不大，KNN算法的运行时间会减少，但不明显，算法优化效果一般。当阈值设置的较大时，对于方差值范围较小的数据集，过滤掉的特征会更多，模型的准确率会有明显的降低，KNN算法的运行时间会更少，此时，算法在时间上的优化是以准确率的大幅度降低为代价;对于方法值范围较大的数据集，过滤掉了无效的特征，模式准确率会有提升，KNN算法的运行时间也会减少，算法的优化效果明显。

4  结  论

本文采用方差过滤进行特征预处理，将特征数由784个减少至392个，针对KNN算法与交叉验证的运行，运行时间减少了1/3，准确率。使用此数据集在之后采用卡方过滤、F检验和互信息法，进行预处理实验的结果中，特征数都有一定程度的减少，准确率却不低于未进行特征预处理的运行结果，甚至出现了准确率被提高的结果。利用特征预处理可有效提高运算的效率，如果对于数据集所对应的业务有所了解，将更有利于特征的预处理，为运算效率的提升提供更优化的数据集。

参考文献：

[1] 吴星辰.基于KNN算法的城市轨道车辆时序数据异常检测 [J].智能城市，2021，7（22）：20-21.

[2] 张燕宁，陈海燕，常莹，等.基于KNN算法的手写数字识别技术研究 [J].电脑编程技巧与维护，2021（11）：123-124+132.

[3] 王巨灏，蔡嘉辉，王琨等.基于KNN与LOF算法的台区线损异常检测 [J].电工技术，2021（24）：175-177.

[4] 刘云，郑文凤，张轶.卡方校正算法对入侵检测特征选择的优化 [J].武汉大学学报（理学版），2022，68（1）：65-72.

[5] 郭鸿飞.F检验法和T检验法在方法验证过程中的应用探究 [J].山西冶金，2019，42（4）：114-116.

[6] 周育琳，穆振侠，彭亮，等.基于互信息与神经网络的天山西部山区融雪径流中长期水文预报 [J].长江科学院院报，2018，35（8）：17-21.

作者简介：张玉辉（1983.10—），男，汉族，湖南岳阳人，讲师，硕士，研究方向：机器学习。