一种基于自适应滤波的海杂波背景下多目标检测方法
马红光 郭金库 姜勤波 刘志强


摘 要:文章提出一种基于自适应滤波的多目标检测方法。将雷达回波等分成回波矩阵Xi,计算Xi的协方差矩阵并进行特征值分解;利用特征值矩阵D计算奇异谱,估计主分量个数Nev,以Nev>3作为门限判断回波矩阵Xi是否包含目标;通过特征矢量矩阵V构成的自适应滤波器对Xi滤波,估算滤波后回波脉冲的Pareto模型参数,生成Pareto随机序列;采用K-L散度识别目标回波,用峰值检测法确定各个目标位置。通过实测海杂波数据实验,验证了所提方法的有效性。
关键词:海杂波;多目标检测;特征值分解;自适应滤波;K-L散度
中图分类号:TN957.51 文献标识码:A文章编号:2096-4706(2022)04-0072-05
A Multi-target Detection Method Based on Adaptive Filtering in
Sea Clutter Background
MA Hongguang, GUO Jinku, JIANG Qinbo, LIU Zhiqiang
(Xian Daheng Tiancheng IT Co. Ltd. Xian 710026, China)
Abstract: A multi-target detection method is proposed based on adaptive filtering. The radar echo is firstly evenly partitioned into echo matrices Xi. The covariance matrix of Xi is calculated and then the eigenvalue decomposition is performed. The singular spectrum is calculated via the eigenvalue matrix D, and the number of principal components Nev is determined. The threshold Nev>3 judges if targets are contained in Xi. The adaptive filtering is applied to Xi with the eigenvector matrix V. The model parameters of Pareto distribution are estimated for each filtered echo. The random series of Pareto distribution are generated. The target echoesare identified via K-L Divergence. The positions of targets are determined by peak finding technique. Trials have been conducted on the measured sea clutter datasets and the effectiveness of the proposed method is validated.
Keywords: sea clutter; multi-target detection; eigenvalue decomposition; adaptive filtering; K-L divergence
0 引 言
海杂波是雷达波束照射海面时波束覆盖区域产生的回波。海浪宏觀运动及海面不规则的毛细管状运动,使得海杂波具有较强的“非线性、非平稳和非高斯”等特性,致使传统的恒虚警检测器(CFAR)不能适用于海杂波背景下的多目标检测[1]。学者们对海杂波特性的研究由来已久,早期工作主要集中在对海杂波统计学模型的研究上,典型的海杂波统计学模型有Weibull[2]、log-normal和K分布[3,4]。近年来,对实测海杂波信号“尖峰”特性的研究表明,Pareto分布能更加准确地描述这一特性[5]。衡量模型有效性的一个重要前提条件是:在雷达相干处理时间内海杂波必须是平稳的随机过程,以确保可以用恒定的模型参数实现CFAR目标检测。雷达探测海面上弱小目标时,需要增加相干处理时间以增强目标回波能量,与此同时海杂波的非平稳特性也显著增强,以至于不再满足上述前提条件。因此,基于统计学模型的目标检测方法仅适用于相干处理时间短的场合。
为解决上述问题,已有大量研究成果见诸报端:Wu提出了一种基于奇异谱分析的海面小目标检测方法[6];Chen提出了一种利用SVD-FRFT滤波的海杂波压制方法[7];Li提出了一种在强海杂波中检测动目标状态的自适应探测方法[8];翟东奇等提出了基于非线性自适应滤波器的海杂波抑制技术[9];Zhang提出了一种基于改进的快速聚类分段的海杂波中弱小目标检测方法[10];Lang针对高分辨SAR图像目标识别问题,提出了一种基于像素聚类的舰船目标检测方法[11];Su提出了基于混沌理论、径向基神经网络及k-means聚类的海杂波预测方法[12];针对海杂波的非平稳混沌特性,Ma提出了一种非平稳混沌时间序列相空间重构方法[13],在此基础上提出一种基于多尺度有向Lyapunov指数的海杂波中弱小目标检测方法[14]。
上述方法的共同特点是不再依赖海杂波的统计学模型,有效克服了传统方法的不足,但存在计算复杂度较高、部分方法需要运用大量人为标定的训练数据集,这些问题仍是其工程应用的桎梏。为此,本文提出一种基于自适应滤波的海杂波背景下目标检测方法。9C24E143-2BAE-460D-8C58-FABBD0E48C9A
1 方法与步骤
本文所提的基于自适应滤波的海杂波背景下目标检测方法,具有算法简单快捷、不依赖任何目标先验知识,可自动区分海杂波和目标回波等特点。所提方法的流程图如图1所示。
所提方法的计算步骤为:
Step 1:以雷达扫描整个监测海面的回波为对象,根据对海观测雷达天线转动速度ΩE、雷达的波束方位宽度θA和脉冲重复频率PRF,计算每个方位向回波脉冲数量:
(1)
Step 2:按照np将雷达扫描整个监测海面的回波脉冲N等分为Nbin个方位向单元回波,构成对应各个方位向的回波矩阵Xi,Xi为np×nt的矩阵(i=1,2,…Nbin),Nbin=floor(N/np),floor(·)为取整函数,nt为回波脉冲采样点数。
Step 3:计算回波矩阵Xi的协方差矩阵:
(2)
其中,H表示回波矩阵的共轭转置,C为np×np的正定Hermitian矩阵。
Step 4:对协方差矩阵进行特征值分解:
[V D]=eig(C)(3)
其中,D为对角矩阵,其对角线元为C的特征值,V各列为各个特征值对应的特征矢量。
Step 5:提取D的对角线元,按降序重排C的特征值,并相应调整V各列的位置,计算奇异谱:
(4)
其中,dj为重新排序后C的特征值。
Step 6:对回波矩阵进行自适应滤波:
Xi=VTXi (5)
其中,T为矩阵转置。
选择一个门限Thr,将满足σj≥Thr的特征值个数Nev作为主分量(Principal component, PC),将其余特征值作为次分量(Minor component, MC),将滤波后的回波Xi分为Sp和Sm。
Step 7:若Nev≤3,判定回波Xi为海杂波,反之,对Sp和Sm做进一步处理(Sm可用于弱小目标检测)。
Step 8:采用最大似然估计依次估算Sp(或Sm)各行的Pareto分布模型参数(a,b):
(6)
其中,x为回波的瞬时幅度,nt为回波脉冲采样点数,Γ(·)为伽马分布函数,a为形状参数,b为尺度参数。
利用估计的模型参数(a,b),通过Pareto随机数发生器生成与回波信号等长的随机序列y,采用Kullback-Leibler(K-L)散度识别目标回波脉冲:
(7)
其中,Px为回波信号幅度的概率密度函数,Qy为随机序列y的Pareto分布函数。
将K-L散度最大值对应的回波信号识别为目标回波。
Step 9:采用Matlab的findpeaks函数确定目标所在距离:
(8)
其中,x=p或m,Sx(i,:)中,i为回波矩阵Sp或Sm被识别为目标回波所在的行号,输入选项‘MinPeakProminence、minP为最小峰值显著性;函数的输出pks、locs、w、P分别为被确认有效的谱峰高度、位置、宽度和显著性。
最小峰值显著性的估计方法是,首先用没有最小峰值显著性约束的findpeaks测量回波信号的全部峰值显著性P,计算P的均值μ和标准离差σ,令:
minP=μ+nσ,n?[1,3] (9)
可得自适应minP,确保目标检测门限值的合理性。
Step 10:重复S2~S9,即可获得整个监测海面上目标的位置。
在步骤S3回波矩阵Xi中,每一行对应一个回波基带信号的采样值vi=xi+jyi,回波的瞬时相位θi=tan-1(yi/xi),所构造的协方差矩阵C的对角线元为每个回波脉冲瞬时功率,非对角线元,保留了回波的瞬时幅度、相位特征与脉冲间的相干特性,经步骤S4~S6后,所得到是根据海杂波与目标回波在幅度和相位上的不同而进行的信号正交分离的结果,与仅从回波幅度特征區分杂波与目标的方法相比具有明显优势。
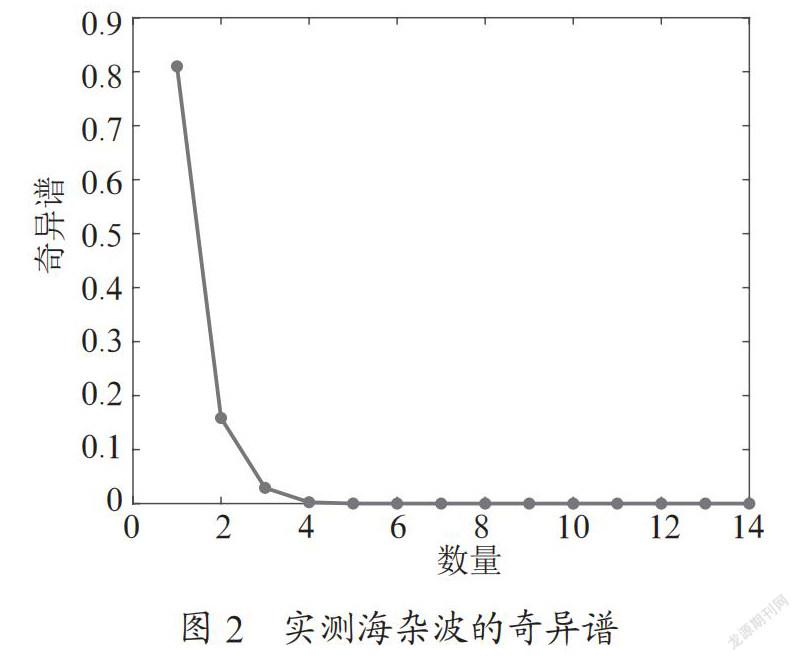
在步骤S6~S7中,选择门限Thr和确定区分海杂波与目标回波的原则是所提方法的核心问题。对大量海杂波数据的研究表明,海杂波主要由Bragg、白冠(Whitecap)和突发(Burst)散射形成[4],其中,Bragg散射为入射电波在海面产生的谐振现象,在海表面毛细管状波和海浪重力波这两个不同尺度的波长上都会发生。在一定的海况下,海浪会按其运动周期发生后向散射,来自多个海面波的回波就会进行相干叠加形成雷达接收的回波,是海杂波的主要成分。白冠是由波浪上端变窄下端变宽后形成类似劈状的结构而产生的散射。但并非所有劈状结构都能形成白冠散射,只有当劈状结构破碎后才形成白冠,因此白冠在海杂波中所占比例较低。突发散射是由即将破碎的波浪面产生的后向散射,波面在破碎前形状呈陡峭的平面状,由此产生较强的镜面反射。突发散射在HH极化下具有很强的功率;但在VV极化下,海面动态结构形成的多径效应使得突发散射变得极其微弱,有时候甚至可以忽略。图2为烟台养马岛实验场实测海杂波的奇异谱[15]。
由图2可知,Bragg散射占比80%以上,白冠散射约占10%~20%,而突发散射的占比在0.01%左右。因此,门限Thr=0.001是我们在实验中选取主分量的门限。
主分量个数Nev≤3时,回波矩阵Xi中不包含目标,反之,回波矩阵Xi中包含目标。图3为烟台养马岛海杂波数据20200722150408_798_scanning.mat的主分量数量Nev在雷达扫描方位向的变化情况,雷达主要参数及实验场地详见[16]。如图3所示,T1脉冲为雷达工作于“模式2”发射的第1个单载频脉冲(载频fc=9.3 GHz,脉宽τ=40 ns),T2脉冲为雷达工作于“模式2”发射的第2个LFM脉冲(载频fc=9.3 GHz,脉宽τ=3 μs,调频斜率K=75),2个脉冲瞬时带宽相同,均为Bw=25 MHz,脉冲重复频率PRF=1.6 kHz,天线水平波束宽度θA=1.2°,天线转速ΩE=24 r/min,因此,各方位向的脉冲数np=14。由图3的实验结果并对照[15]中的目标场景,选择Nev>3作为目标检测的门限是合理的。9C24E143-2BAE-460D-8C58-FABBD0E48C9A
在确定回波中包含目标之后,从自适应滤波后的回波中识别目标回波是所提方法的创新点之一。传统方法主要是在欧氏空间通过计算幅度之间的差异来区分海杂波与目标回波,虚警和漏报概率较高。相较于传统方法,采用信息几何方法处理这一问题有明显的优势,海杂波与目标回波被视为黎曼空间中随机流形上的点集[17],利用K-L散度可正确估算随机流形上点之间的差异,具有稳定可靠的识别率。
这里需要说明步骤S8中为何要分别估计每个滤波后回波的Pareto分布模型参数(a,b)的原因,图4为滤波后回波Pareto分布模型参数(a,b)随方位向变化的曲线,为准确判断回波属性,需要分别估计其模型参数,生成对应的Pareto随机序列,降低误判概率。
图4 Pareto分布模型参数(a,b)在方位向的变化图
在步骤S9中,采用回波信号中最小峰值显著性minP作为检测目标的门限,峰值显著性P=pks/w,即峰值高度与宽度之比,这一门限综合考查峰值高度和宽度,并根据回波的动态特性自适应地调整门限,在确保对目标可靠检测的同时还可以有效降低“海尖峰”造成的虚警概率,使整个目标检测过程具有恒虚警检测特性。
2 实验结果及有效性分析
为验证所提方法的有效性,我们对2020年7月8日15时04分08秒在烟台养马岛实验场实测海杂波数据集798~808进行了实验研究,每个数据集的目标检测结果基本一致,这里仅给出20200722150408_798_scanning.mat的结果。
表1、表2仅给出回波矩阵主分量对应的目标检测结果,其中方位角为回波矩阵对应方位角的均值。表1为T1脉冲回波全部的目标检测结果,观察滤波后的回波可知,T1回波存在較强的近程杂波,为此,将距离小于2 km的目标判断为近程杂波,如图5所示。
表1 T1脉冲主分量回波目标检测结果
由于T2脉冲功率远大于T1脉冲功率,所检测到的目标数量远多于表1中的目标数量,为便于比较,表2仅列出了与表1目标相近的方位向目标检测结果。图5为雷达波束方位角为5.65°时的PC、MC回波,经计算K-L散度,图5(a)的第1行被判定为目标回波,目标检测结果如表1所示,除近程杂波外,仅探测到6.73 km处的目标;对比表2的目标检测结果可知,除6.365 km的目标外,11.252~13.886 km这一范围内存在连续12个峰值点,对照[15]给出的目标场景,该方位向存在一座航道浮标与浮标相距一段距离的芝罘岛,因为T1脉冲功率小,该岛屿为弱目标,不能在PC回波中被检测到,但在MC回波中,该岛屿的回波清晰可见。
由上述实验结果可知,本文所提方法能够准确区分海杂波与目标回波,具有探测海面弱小目标的能力。
3 结 论
海杂波背景下的目标检测、识别与跟踪是雷达信号处理领域中的热点问题,经过长期的研究与探索,已取得丰硕成果。近十年来,随着非线性科学的不断进步,尤其是人工智能技术的快速发展,出现了许多新颖的信号处理方法,但受限于雷达信号处理对实时性等方面的要求,这些方法多数仍处于理论探索阶段,尚不能用于工程实践。西安大成科技的研究团队长期致力于该项研究工作,在关注新理论、新方法的同时,更加注重解决工程中的实际问题,本文所提方法正是基于此目的而取得的阶段性成果,我们对该成果的工程应用充满信心。
参考文献:
[1] 逯旺旺,杨勇,张斌,基于谱峭度特征识别的海杂波弱小目标检测方法 [J].现代信息科技,2020,4(4):31-35.
[2] FAY F A,Clarke J,Peters R S. Weibull distribution applied to sea-clutter [C]. London:Proc. IEE Conf. Radar77,1977.
[3] SAYAMAS,SHUJI,SekineM,et al. Log-normal, log-Weibull and K-distributed sea clutter [J].IEICE Transactions on communications,2002,85(7):1375-1381.
[4] WARD K D,TOUGH R J A,WATTS S. Sea Clutter: Scattering, the K Distribution and Radar Performance [M].London:The Institution of Engineering and Technology,2013.
[5] GRAHAM,VICTOR,WEINBERG. Noncoherent Radar Detection in Correlated Pareto Distributed Clutter [J].IEEE Transactions on Aerospace and Electronic Systems,53(5):2628-2636.
[6] WU X J,DING H,LIU N B,et al. A Method for Detecting Small Targets in Sea Surface based on Singular Spectrum Analysis [J].IEEE Transactions on Geoscience and Remote Sensing,2021,60:1-17.
[7] CHEN Z,HE C,ZHAO C,et al. Using SVD-FRFT Filtering to Suppress First-Order Sea Clutter in HFSWR [J].IEEE Geoscience and Remote Sensing Letters,2017,14(7):1076-1080.9C24E143-2BAE-460D-8C58-FABBD0E48C9A
[8] LI Y,SIRA S P,MORAN B,et al. Adaptive Sensing of Dynamic Target State in Heavy Sea Clutter [C]//2007 2nd IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing. St. Thomas:IEEE,2007:9-12.
[9] 翟东奇,江朝抒,邓晓波,等.基于非线性自适应滤波器的海杂波抑制技术 [J].航空科学技术,2018,29(6):73-78.
[10] ZHANGH H Y,ZHAO Z,XIAO F X. Robust Detection Method of Small Targets in Sea-Clutter via Improved Fast clustering Segmentation [C]//2016 8th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC). Hangzhou:2016:123-126.
[11] LANG H T,XI Y Y,ZHANG X. Ship Detection in High-Resolution SAR Images by clustering Spatially Enhanced Pixel Descriptor [J].IEEE Transactions on Geoscience and Remote Sensing,2019,57(8):5407-5423.
[12] SU X H,SUO J D. Prediction of Sea Clutter Based on Chaos Theory with RBF and K-mean Clustering [C]//2006 CIE International Conference on Radar. Shanghai:IEEE,2006:1-4.
[13] MA H G,ZHANG C L,LI F. State space reconstruction for nonstationary time-series [J].Journal of Computational and Nonlinear Dynamics,2017,12(3):031009.
[14] WANG R,LI X Y,MA H G. Detection of small target in sea clutter via multiscale directional Lyapunov exponents [J].Sensor Review,2019,39(6):752-762.
[15] 劉宁波,丁昊,黄勇,等.X波段雷达对海探测试验与数据获取年度进展 [J].雷达学报,2021,10(1):173-182.
[16] 刘宁波,董云龙,王国庆,等.X波段雷达对海探测实验与数据获取 [J].雷达学报,2019,8(5):656-667.
[17] 赵兴刚,王首勇.基于K-L散度和散度均值的改进矩阵CFAR检测器 [J].中国科学:信息科学,2017,47(2):247-259.
作者简介:马红光(1959—),男,汉族,河南郑州人,教授(总师),博士,主要研究方向:非线性信息处理、目标探测与识别;郭金库(1980—),男,汉族,山东菏泽人,副教授(CEO),博士,主要研究方向:复杂电磁环境下目标检测与识别;姜勤波(1976—),男,汉族,江苏丹阳人,副教授,博士,主要研究方向:复杂系统建模与仿真、电子对抗;刘志强(1979—),男,汉族,四川崇州人,副教授,博士,主要研究方向:复杂系统建模与仿真、电子对抗。9C24E143-2BAE-460D-8C58-FABBD0E48C9A

