山西省新型冠状病毒肺炎疫情发展状况的模型拟合研究

李 阳，刘宝亮

(1.山西大学数学科学学院，山西太原 030006；2.山西大同大学数学与统计学院，山西大同 037009)

关键字：新型冠状病毒肺炎；SEIR 模型；疫情发展状况

据中国卫健委发布的截至2020 年2 月20 日24时新型冠状病毒肺炎疫情最新情况以及疫情对于我们生活的影响，应该深刻认识到保证新型冠状病毒感染的肺炎疫情防控工作的重要性。

在2020 年严峻的疫情形势下，习近平总书记发表重要讲话[1]，将疫情摆在及其重要的位置，对新型冠状病毒感染的肺炎疫情防控工作作出重要指示，强调全体人民要全面贯彻坚定信心、同舟共济、科学防治、精准施策的要求，坚决打赢疫情防控阻击战。

对于突如其来的新冠肺炎，张晓晴等[2]从医学角度对其症状、作用机制等方面作了详细论述，表明血管紧张素转化酶有很大可能是新型冠状病毒感染细胞的介导受体；林挺葵等[3]在对粤西地区及各地级市新冠肺炎疫情趋势预测分析中也提到了新冠病毒与好多疾病是相关的。基于SIR 模型，罗荣桂等[4]进行了技术扩散模型的研究，而技术扩散过程与传染病蔓延过程相类似，并且SIR模型本身就是传染病模型中的经典模型，所以学者们注意到用SIR传染病模型对该疫情问题进行数学建模是合理的。武文韬等[5]运用SIR 模型对广东省新冠肺炎疫情流行趋势进行预测，并以微分方程的形式表示该模型的基本构成，然后利用指数平滑法进行预测。杨雨琦等[6]用SIR模型对此次疫情了研究，他们用MATLAB进行编程，对模型中的微分方程组进行求解，计算出模型中的未知系数，从而预测疫情发展趋势。徐恭贤等[7]建立了带有潜伏期及终身免疫的SARS 流行病的SEIR 动力学模型，根据部分国家或地区的SARS疫情数据，对模型中的参数进行了参数辨识，对SEIR 模型进行了更深层次地解释。蔡洁等[8]利用该模型对武汉市疫情状况进行模拟预测时对于模型中的参数进行了适当地估计，一定程度上解决了用MATLAB 获取参数的难题，为模型中参数的确定提供了科学依据。耿辉等[9]对新型冠状病毒肺炎疫情中相关干预措施的作用进行了评价，利用python 建立SEIR 模型。可以基本得出：基于SEIR 模型研究山西省新冠肺炎疫情的发展状况是较合适的，然后进一步研究不同管控强度对新冠肺炎疫情的影响，所得结论可为今后新冠疫情管控预测及社会政策制定等提供依据。

1 模型的建立

1.1 SIR模型

基本假设：

(1) 在疾病传播期内所考察地区的总人数N不变，既不考虑生死，也不考虑迁移。人群分易感者(Susceptible)、感染者(Infective)、恢复者(Removed)三类，t时S(t),I(t),R(t)，t时刻这三类人在总人数中所占的比例分别记作s(t),i(t)和r(t)，即单位时间内（每天）的易感者表示为s(t),感染者为i(t),恢复者为r(t)；

(2) 每个感染者每天有效接触的平均人数是常数λ，称为日接触率，也可以称为感染系数（单位时间内感染者i(t)所能感染的人数与易感者s(t)成正比）。当感染者与易感者有效接触时，使易感者受感染变为感染者；

(3) 每天被治愈的感染者占感染者总数的比例为常数μ，称为日治愈率，也可称为恢复系数，感染者被治愈后仍有可能成为感染者，那么可认为是该病毒的平均传染期；

(4) 初始时刻，只有少数个体处于感染状态，其他都是易感状态;

(5)假设疾病的时间尺度远小于个体生命周期，从而不考虑个体的出生和自然死亡;

(6)完全混合，即每一个个体与其他个体接触的机会均等。

由假设(1)可得，整个群体由易感染者，感染者，恢复者构成：

由此，可以得到关于S(t),I(t),R(t)的微分方程：

进而得到关于s(t),i(t),r(t)的微分方程：

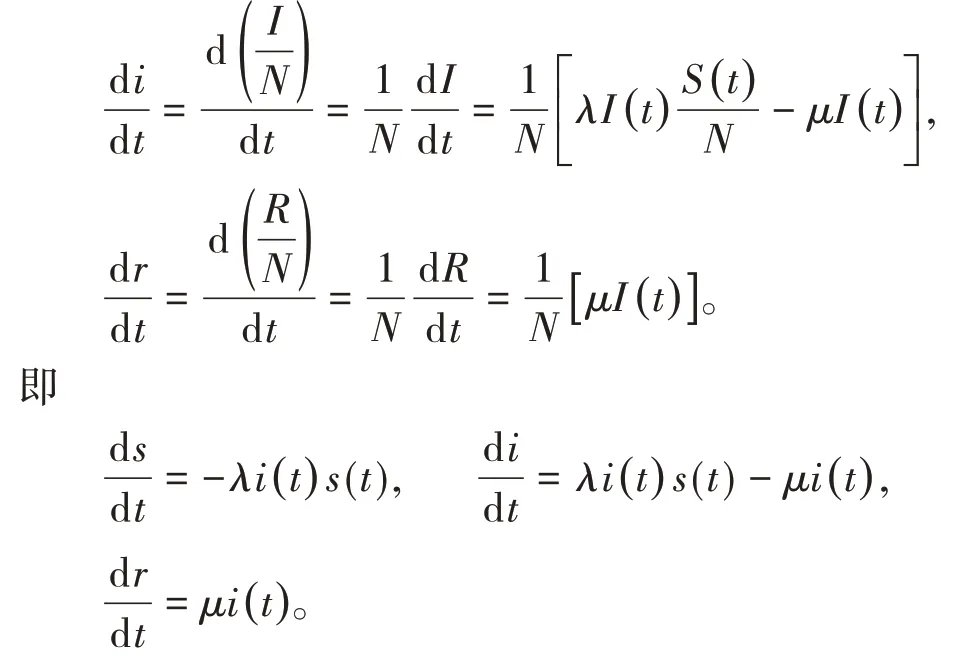
使用MATLAB 软件对以上微分方程组进行求解。首先，要确定感染系数λ和恢复系数μ的取值。可通过统计的自1 月22 日起的山西省新冠肺炎现存确诊、累计确诊、累计治愈人数等官方数据及最小二乘法分别对恢复系数μ与感染系数λ进行估计，然后代入模型中拟合山西省的疫情发展趋势。而实际环境并不能满足上述假设(6)的完全混合，故用人口数作为人口总量进行预测是不准确的，需要用最小二乘的思想估计易感者初值S(0)。

1.2 SEIR模型

针对传染病的传播，尽管有较符合实际的SIR模型，但由于SIR 模型通常不考虑潜伏群的影响及变化，而新冠肺炎的传染是有一定潜伏期的，因此，对SIR模型进行改进，建立SEIR 模型。

采用SEIR 模型模拟新冠肺炎的传播过程是将整个人群分成4 类:S类（易感者）、E类（潜伏者）、I类（感染者）、R类（康复者）四种类型：

S类(Susceptible)：指未得病者，但缺乏免疫能力，与感染者接触后容易受到感染；由于新型冠状病毒所有人群普遍易感染，所以这里S=N-I。（由于多数人在家隔离，所以N并不为所有人，取N=200）；

E类(Exposed)：指接触过感染者，但暂无能力传染给其他人员，对于像新冠肺炎这种潜伏期长的传染病适用，假设最初E=0；

I类(Infectious)：指已被感染传染病者，能够传播给S类成员，将其变为E类或I类成员，根据官方数据易得第一天I=1；

R类(Recovered)：指被隔离或因病愈而具有一定免疫力的人。如免疫力有限，R类成员可以重新转化为S类成员，根据实际情况第一天R=0。

基本假设：

(1)只发生人传人；

(2)现阶段无治疗的特效药和疫苗；

(3)不考虑外界环境等因素对病死率的影响；

(4)忽略人口流动的死亡。

SEIR微分方程：

以下为迭代形式：

模型中各参数含义及取值：

r：感染者每天有效接触的平均人数,据实际情况估计为20人；

β：易感者转化为潜伏者的概率，依据山西省卫健委公布的数据估计得到β≈0.03；

α：潜伏者转化为感染者的概率，约为0.1；

γ：治愈概率，约为0.1。

2 分析与结果（SEIR模型）

用MATLAB 绘制山西省新型冠状病毒现存确诊病例、累计确诊病例、累计治愈病例变化曲线如图1。

图1 显示，山西省在2 月10 日之后，新增确诊病例呈明显下降态势，疫情形势有所好转；于2月初，开始陆续出现治愈病例，并在5天后感染者恢复速率变大；现存感染者人数在2 月10 日之前逐渐增多，约在2 月10 日左右达到峰值，不超过100 人，在这之后逐渐减少。

图1 山西省2020年1月22日-2月20日疫情情况图

用MATLAB 编程，可求出上述模型中微分方程的解，并绘制相应的I(t)，s(t)，r(t)函数（大概截止到2020 年5 月）4 类人群人数变化的大致图像，以反映疫情大致的发展状况，可通过将截止到2 月20 日的图像与图1的比较，发现模型模拟图形与实际图形基本吻合，这在一定程度上可以说明用SEIR 模型模拟疫情发展状况是较为合适的。

进而对2 月20 日之后一直到5 月份的疫情发展趋势进行模拟。

由图2可看出，该疫情于出现第一例感染者后一个多月（即2 月底）达到峰值，且该疫情将在4 月底得到基本控制，与实际情况相比，相差不远，进一步增强了该模型的可靠性。

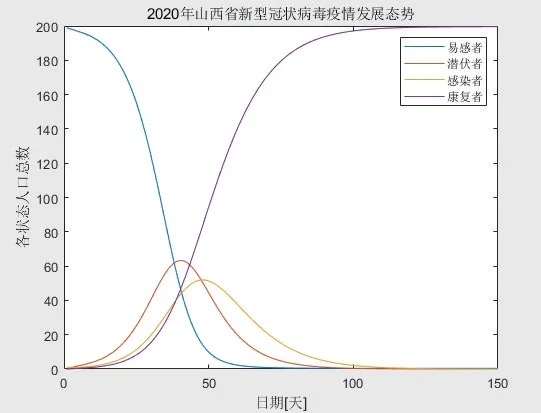
图2 SEIR模型对疫情发展状况的模拟图

进一步在该模型下分析在不同管控强度下防控策略对山西省新冠肺炎疫情发展的影响。

设置了3 种管控强度来分析不同的管控强度对山西省新冠肺炎疫情发展的影响，强度一表示每个易感者每天能接触15 例(设置感染者每天有效接触的平均人数r=15)，强度二表示能接触20 例(设置感染者每天有效接触的平均人数r=20)，强度三表示能接触25 例(设置感染者每天有效接触的平均人数r=25)。这三种强度下管控强度逐渐减小。

由图3～5 可得到：强度二为文中所研究的强度，在管控强度增大时，即在强度一下，感染者所达到的峰值减小；相反，强度减小，即在强度三下，感染者所达到的峰值增大，这表明在不同管控强度下的防控策略对山西省新冠肺炎疫情发展是有影响的。管控强度越大，新冠肺炎疫情发展速度越慢，同时感染者例数越少。

图3 强度一下感染者人数变化

3 结语

在SIR 模型的基础上结合本地疫情特点改进得到SEIR 模型，利用国家卫健委和山西省卫健委官方发布的数据估计模型关键参数，模拟山西省新冠肺炎疫情的发展态势，可以得出一个明显的结论，即山西省疫情在2 月底达到峰值，在4 月底得到基本控制。与实际的新冠肺炎疫情数据相较之下，实际值与模拟值之间的差别并不是特别大，所以可认为SEIR 模型可以较好地应用于研究山西省新冠肺炎疫情的发展状况。

就新冠肺炎本身特点来说，新冠肺炎疫情的传播是一个非常复杂的过程。诊疗标准和检测手段的不同，不同年龄和不同性别的人群感染率的不同，本身健康和本身患有基础疾病感染率的不同，区域人口密度不同对传播的影响等这些因素都会影响到模拟的准确性，进而产生模拟与实际的偏差。

图4 强度二下感染者人数变化

图5 强度三下感染者人数变化