平板锚基础在砂土地基中抗拔承载力
程 力,牛富俊,周 密,姜海强,谢杰辉
(1.亚热带建筑科学国家重点实验室(华南理工大学),广州 510640;2.华南理工大学 华南岩土工程研究院,广州 510640)
随着陆上和海上风能发电技术的不断发展,未来海上风电行业必然会进入更深的水域,以获取强劲的风力资源,并尽量减少风电场对沿海地区的视觉和环境影响[1]。由于深水区(海水深度d>60 m)抵抗环境力所需的结构尺寸更大,安装所需的技术更为复杂,传统的陆上及浅海基础(例如,单桩基础和重力式基础等)将变得不切实际和不经济[2-3]。通过锚基础提供足够的抗力,将浮式海上风电机的下部结构锚定在海床以支撑深海处风机的运行成为一种可行方法[4]。
锚的类型包括桩锚、拖锚、板锚、螺旋锚和灌浆锚以及这些类型的组合[5-6],其中,平板锚是适用于抵抗海上浮式平台等结构上拔力的锚基础之一[7],如图1所示。条形锚基础在砂土中的抗拔承载力通常可以用抗拔承载力系数Nγ表示为
(1)
其中:P为锚基础单位长度的上拔力,B为条形锚基础的宽度,H为条形锚基础的埋置深度,γ′为砂土的有效重度。
许多学者采用不同的方法对条形平板锚基础在砂土地基中的抗拔承载力展开了相关研究,如理论解[8-12]、物理模型试验[13-15]和有限元方法[16-19]。Murray和Vesic等[8-9]提出的理论解均基于砂土相关联的流动法则(即φp=ψp,其中,φp,ψp为砂土的峰值摩擦角和峰值剪胀角),其假设平板锚基础上部砂土的滑动破坏面角度θ=φp=ψp(如图1所示),且摩擦角的变化可以唯一地反映剪胀角对条形平板锚抗拔承载力的影响。然而,在实际中,采用非关联流动准则(即φp≠ψp)描述砂土的力学行为可能更为准确,且Rowe等[17]通过有限元数值计算表明剪胀角对平板锚基础的抗拔承载力具有显著的影响。
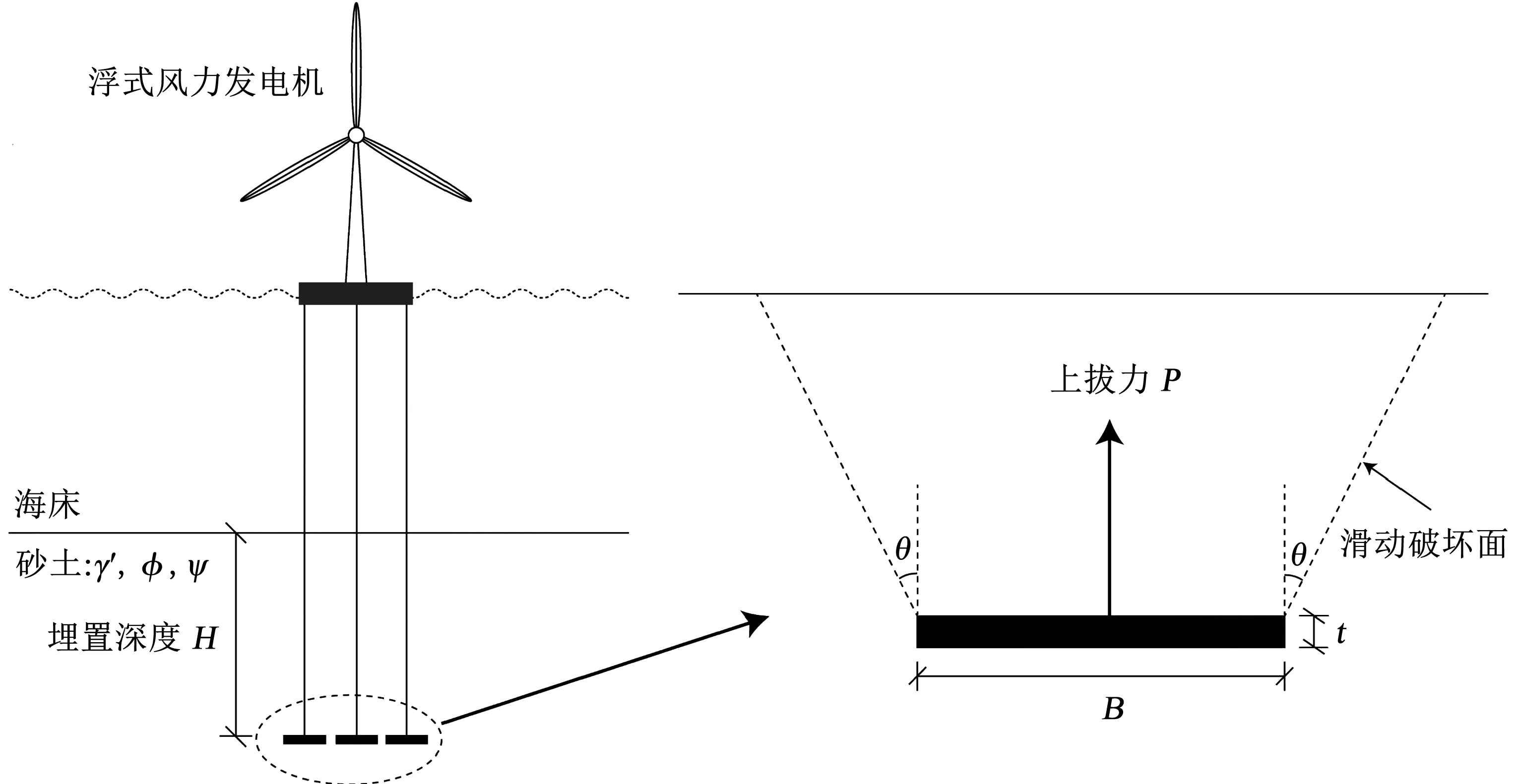
图1 水平锚基础的应用
为了考察砂土剪胀作用对条形平板锚抗拔承载力的影响,White等[12]提出了平面应变条件下非关联流动准则的极限平衡模型,即
(2)
Fps=tanψp+C(tanφp-tanψp)
(3)
式中:Fps为平面应变条件下的上拔系数,C为估计破坏平面上的法向应力常量,表达式为
C=(1+K0)/2-(1-K0)cos(2ψp)/2
(4)
式中K0为静止土压力系数。在上述公式中,锚基础上部砂土层的破坏滑动面从板的侧面向上延伸到土体表面,其与竖直方向的夹角θ=ψp<φp。当采用MC模型的相关联流动法则(φp=ψp)时,上述公式与Murray等[5]提出的上限理论解一致。White等[12]假设在上拔荷载作用下破坏面上的法向应力没有发生改变。然而,通过对砂土的三轴压缩试验发现,对于中密砂及密砂,砂土存在着较明显的应变软化现象[20]。此外,Dickin等[13]通过离心机试验研究条形平板锚基础在中等密砂及密砂中的抗拔承载力,发现理论解均高于离心机试验的试验结果。因此,上述理论解均不能准确地预测条形平板锚基础在中密及密砂土层中的抗拔承载力。
采用二维有限元方法对条形锚基础在中密-密砂土地基中的抗拔承载力展开相关研究。采用修正Mohr-Coulomb(MMC)模型模拟砂土应变软化的力学特性,并开发相应的用户子程序。通过与理论解对比验证该模型的正确性。通过一系列的参数分析,探究锚基础的摩擦因数、埋置深度以及砂土的相对密度对抗拔承载力系数的影响。基于数值计算结果,对平板锚基础在中密及密砂地基中不同深度的抗拔承载力系数公式进行校正。
1 有限元数值分析
使用商业有限元软件ABAQUS/Explicit(版本6.14,Dassault Systèmes,2014年)方法对平板锚基础进行2-D平面准静态分析。相比Abaqus/Standard分析,使用Abaqus/Explicit准静态分析的主要优点是平板板锚可以向上移动相对较大的距离,同时在很大程度上避免了使用Abaqus/Standard时遇到的网格畸变(特别是在剪切应变局部区域)导致计算不收敛的问题。因此,使用Abaqus/Explicit可以更好地模拟集中在剪切带上的大应变[21]。本部分首先对砂土的本构模型进行描述,然后介绍有限元模型和模型几何尺寸及参数。
1.1 MMC砂土本构模型
部分学者采用Abaqus有限元软件内置的理想弹塑性MC模型表示致密砂和中密砂的力学响应[22-25]。但MC模型有一些固有的局限性,例如,一旦土体单元达到屈服应力(由MC破坏准则定义),则使用恒定剪胀值,表明密砂将随着剪切继续剪胀。而室内试验表明,在剪切力作用下,剪胀角逐渐减小到零,土体单元达到临界状态。
为简单地描述中等密砂及密砂土的力学行为,Hu等[26]采用修正Mohr-Coulomb(MMC)模型,其中,移动摩擦角(φ)和移动扩张角(ψ)随塑性剪应变(ξ)的变化而变化,如图2所示。MMC模型在涉及大变形时成功地应用于各种地基-地基相互作用分析,包括纺锤形基础、海底管道和沉箱基础分析[21,26-28]。MMC模型假设摩擦角从初始值φini线性增大到峰值φp,然后线性减小到接近临界状态φcv。对应于峰值摩擦角和临界状态的塑性剪应变临界值分别表示为ξp和ξcv。在ξ≤ 1%时,剪胀角保持为0,然后迅速增加到峰值,此时ξ= 1.2%。然后剪胀角保持在峰值剪胀角ψp后线性减小到0。几乎所有的砂土最初都是剪缩逐渐变成剪胀,但负剪胀角会导致MMC模型计算不收敛,因此,初始的剪胀角简化为0。每个增量步的塑性剪应变增量计算式为
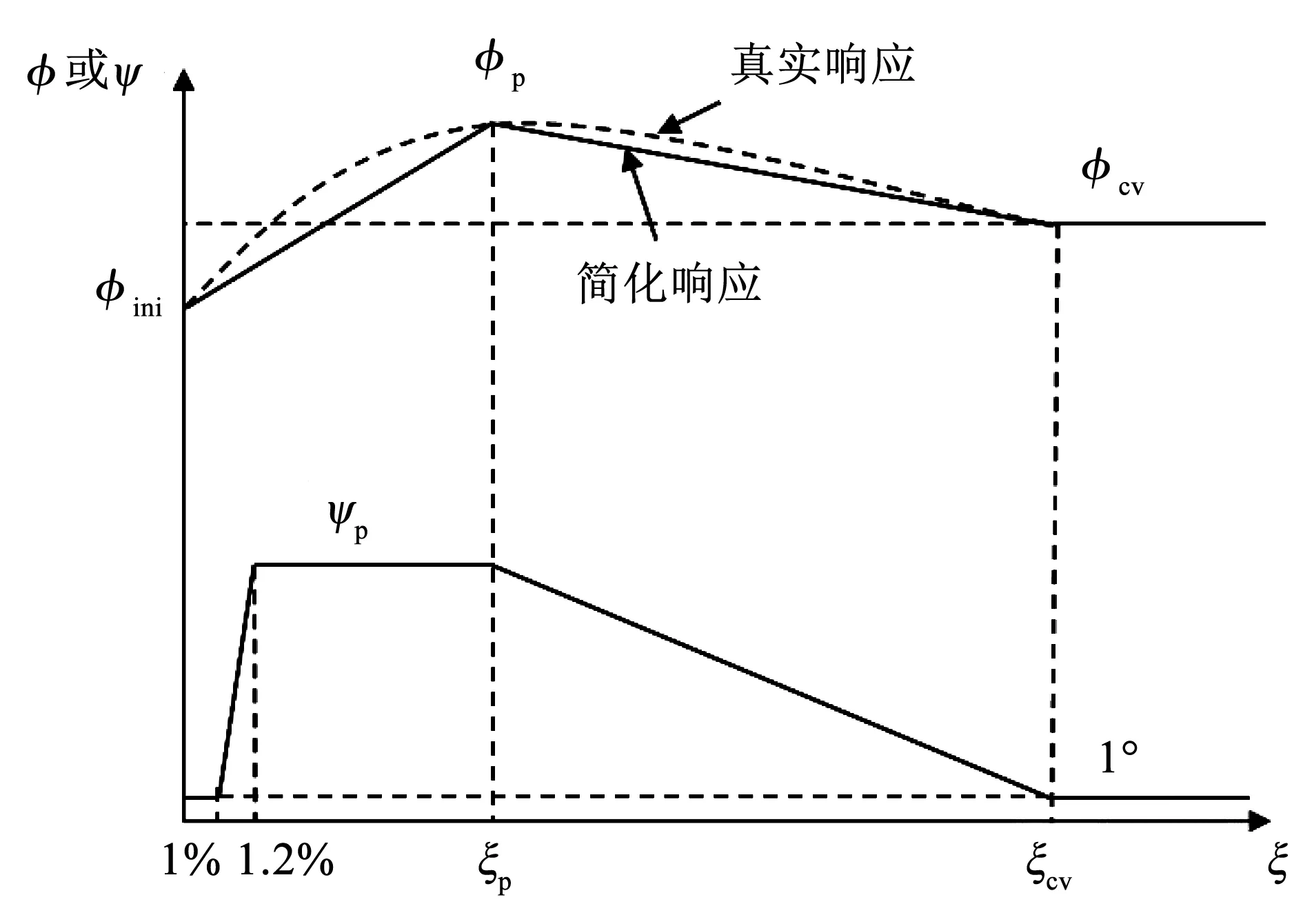
图2 修正Mohr-Coulomb(MMC)模型
(5)
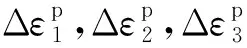
峰值摩擦角φp以及峰值剪胀角ψp由Bolton等[29]公式确定,该公式将摩擦角φ和剪胀角ψ与相对密度和应力水平关联为
φp-φcv=AψIR
(6)
φp-φcv=kψψp
(7)
(8)
对于三轴应力状态下,Aψ=3.0,kψ=0.48;对于平面应变状态下,Aψ=5.0,kψ=0.80。Aψ和kψ的值因砂石矿物学、细粒含量和砾石含量而异[30-32]。IR为相对密度指标(0≤IR≤4.0)。式(8)中,R=1,Q随土体类型而变化(例如,对于纯净的石英砂,Q=10;对于较脆弱的土体,Q<10[29])。
峰值塑性剪应变ξp根据Roy等[18]的建议确定为
(9)
式中:C1、C2和m为土体参数,p′为平均有效应力,pa为大气压力(100 kPa)。根据石英砂的三轴压缩试验结果可估算得到C1=0.22,C2=0.11,m=0.25,ξcv=0.35[21]。图3为峰值塑性剪应变ξp随砂土相对密度Dr和平均有效应力p′的变化情况。可以看出,在归一化有效平均应力p′/pa=10,Dr=40%时峰值塑性剪应变比Dr=100%时峰值塑性剪应变大约68%。为保证三维有限元数值模拟的稳定性,采用最小剪胀角ψ为1.0°,并规定砂土的内聚力c=0.1 kPa。在所有的计算分析中,砂土的杨氏模量E均为20 MPa。
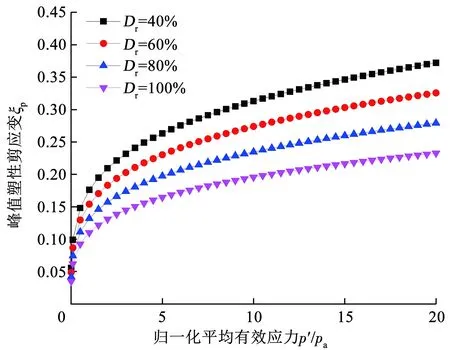
图3 塑性剪应变与相对密度及平均有效应力的关系
在Abaqus有限元软件中,上述MMC模型不是该软件内置模型,不能直接应用。采用Fortran语言开发了适用于Abaqus/Explicit分析的VUSDFLD用户子程序。该子程序中,每个时间增量步结束后,应力应变分量都直接被调用,通过式(5)~(9)计算平均应力p′及塑性剪应变ξ。p′和ξ分别定义为两个场变量FV1和FV2。在输入文件中,通过式(5)~(9)计算得到的移动摩擦角和剪胀角以表格形式定义为p′和ξ的函数。在分析过程中,计算程序调用该子程序并通过场变量的值更新移动摩擦角φ和移动剪胀角ψ的值。
1.2 有限元模型
考虑到对称性的优点,建立了矩形砂土区域和平板锚的模型。砂土域中的网格由四节点双线性四边形,且具有减缩积分和沙漏控制的平面应变单元(CPE4R)组成。为避免边界效应对数值计算结果的影响,锚基础距砂土区域的顶部及右侧的距离分别为H、1.5H,锚基础距砂土区域的底部为2B。平板锚基础与参考点绑定且设置为刚体。本研究中使用的典型网格如图4所示。
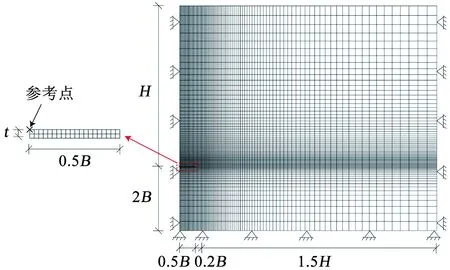
图4 有限元网格
采用Abaqus/Explicit中的接触面法对锚-土界面进行模拟。平板锚基础与周围砂土之间的摩擦行为采用标准库仑摩擦模型。临界摩擦应力τcrit与法向接触压力pc成正比,可表示为τcrit=μpc,其中,μ为摩擦因数,表示为μ=tanφμ,φμ为砂土和平板锚之间的界面摩擦角。φμ一般为峰值摩擦角的50%~100%[33],本研究μ采用0.30[21]。
所有分析分两步进行。在第1步中,采用重力模拟初始地应力,静止土压力系数(K0)根据简化Jaky等[34]的表达式计算:
K0=1-sinφcv
(10)
第2步,将竖直向上的速度边界条件施加在平板锚基础的指定参考点处。
1.3 模型几何尺寸及参数
对宽度为B、厚度为t的条形平板锚基础在深度为H的均质砂土层中的抗拔承载力进行分析。在所有分析中,锚基础宽度B=1 m,t/B=0.05[18]。对于砂土,考虑的参数主要包括黏聚力c, 移动摩擦角φ和剪胀角ψ以及砂土的有效容重γ′。砂土的有效容重γ′=9 kN/m3,临界状态角φcv与初始摩擦角φini取相同值,即φcv=φini[28]。为探究平板锚基础在砂土地基中承载力,在计算分析中采用砂土的相对密度Dr为40%~100%,埋置深度H/B为1.0~10.0,摩擦因数μ为0~1.0。
为考察网格尺寸对平板锚基础抗拔承载力计算结果的影响,在相同的条件下(φcv=32.0°、H/B=3.0、Dr=70%、μ=0.3),采用3种不同的网格密度hmin=0.2t、hmin=0.5t和hmin=1.0t(hmin为网格的最小高度)进行网格敏感性分析,如图5所示。可以看出,网格的密度对抗拔承载力曲线几乎没有影响。因此,选择hmin=0.5t足以提供精确的有限元结果和计算效率。在图5中,随着竖向位移增加,锚基础的抗拔承载力不断增加至稳定值,此时为锚基础的最大抗拔承载力Pu。表1总结了本研究中进行的所有分析,其中,Dr<33%代表松砂。
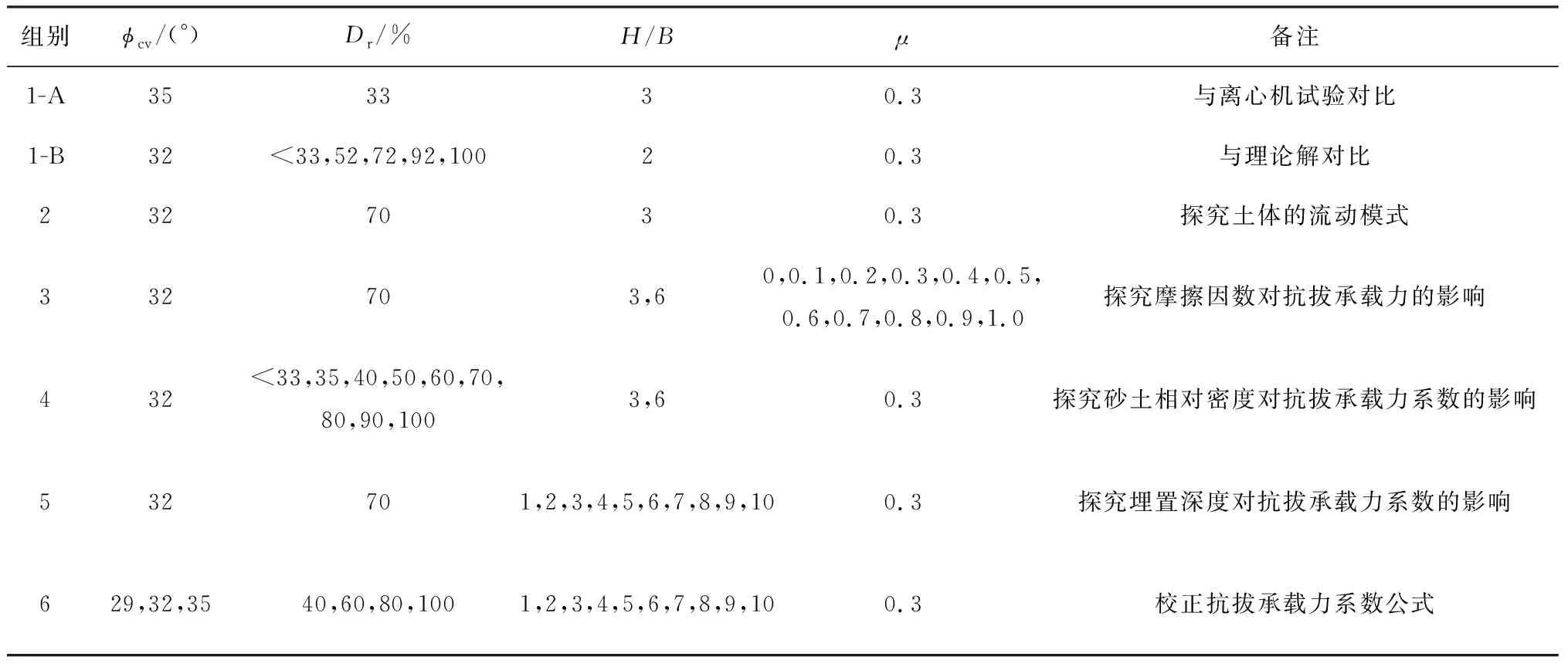
表1 计算参数
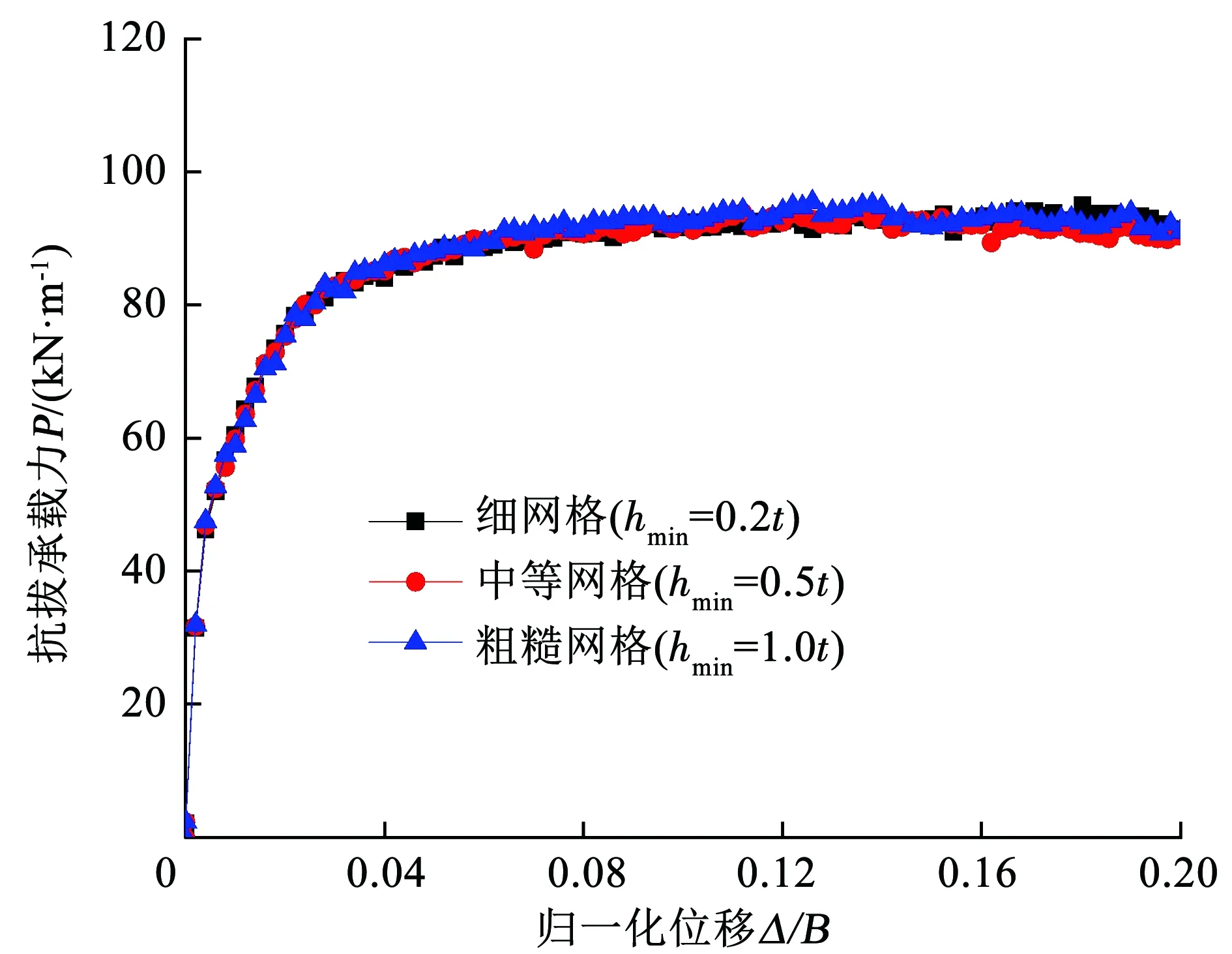
图5 网格敏感性分析
2 计算分析
2.1 数值结果验证
为验证数值计算结果的可靠性,采用两组算例与文献中的结果进行对比验证。
第1组算例(表1 组1-A)中的参数与离心机试验中参数保持一致,分别为φcv=35°,Dr=33%(φp=38.3°,ψp=4.1°),H/B=3,μ=0.3。图6(a)为采用MMC模型计算得到的归一化上拔位移-抗拔承载力系数曲线与Dickin等[13]的离心机试验数据对比。可以看出,随着条形平板锚基础竖向位移的增加,抗拔承载力系数先增加后减小。数值计算中峰值承载力对应的位移小于离心机试验中峰值承载力对应的位移,这主要是由于数值计算中采用砂土的弹性模量高于离心机试验中砂土的弹性模量,而弹模的大小对峰值承载力没有影响[23]。数值计算得到的峰值承载力系数为2.38,离心机试验中的结果为2.45,二者相差3%。
第2组算例(φcv=32°,Dr从20%变化到100%,H/B=2,μ=0.3,表1组1-B)分别采用MC模型和MMC模型计算的结果与Murray[8]及White等[12]的极限平衡理论解进行对比,结果如图6(b)所示。可根据式(5)~(9)计算得到在不同相对密度Dr时峰值摩擦角φp及峰值剪胀角ψp的值。从图6(b)可以看出,当采用相关联流动准则(φ=φp=ψ=ψp)的MC模型时,除摩擦角φ≥ 55°外,MC有限元结果与Murray等[8]提出的上限解基本吻合。当采用非相关联流动准则(φ=φp,ψ=ψp)的MC模型时,有限元的结果基本与White等[12]的理论解一致。当采用非相关联流动准则(φcv≤φ≤φp,1.0°≤ψ≤ψp)的MMC模型来考虑中密砂及密砂的应变软化行为时,计算得到的抗拔承载力系数均小于理论解。当Dr=100%,Murray[8]和White等[12]的理论解比数值解分别高出约57%和29%。因此,该承载力系数计算方法需要进行校正。
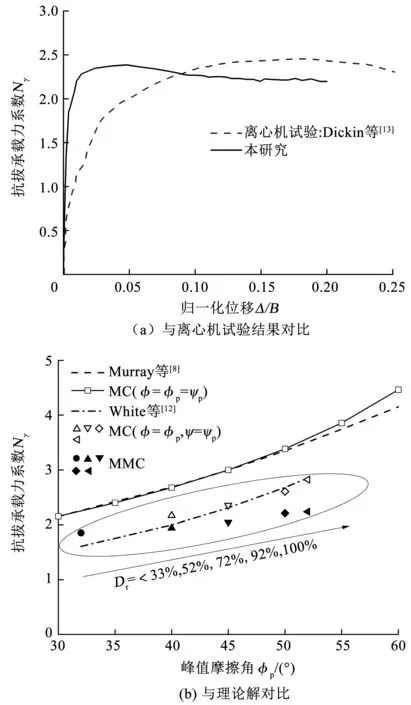
图6 MMC模型验证
综上,本文选取的计算方法是可靠的,可以很好地模拟条形平板锚基础的竖向抗拔承载力。
2.2 土体流动破坏机制
为探究条形锚板基础在上拔过程中砂土的破坏模式,采用算例φcv=32.0°,H/B=3.0,Dr=70%(φp=44.5°,ψp=15.6°),μ=0.3(表1组2)。图7为不同位置平板锚基础周围的塑性剪应变的变化。在MMC模型中,当ξ≥0.35时,土体到达破坏状态(临界状态)。当锚基础的上拔位移较小时(Δ/B=0.1,图7(a)),锚基础右上区域出现局部的破坏滑动面,该滑动面的倾角(与竖向夹角)θ约等于峰值剪胀角ψp。这与Liu等[15]通过平板试验得出破坏时滑动面的倾角与土的峰值剪胀角相对应的破坏模式一致。当锚基础的上拔位移达Δ=0.2B时,局部破坏滑动面沿着倾角θ的方向向上延伸。与Liu等[15]假设的破坏模式不同的是,从图7(b)可以看出,有部分破坏面沿着θ≈1°的方向向上延伸。这可能是由于锚板周围砂土达到破坏,砂土的峰值摩擦角φp和峰值剪胀角ψp分别减小到32°和 1°。此时,随着上拔位移的增加,平板锚上部的砂土出现沿θ≈ψp=1°方向的破坏模式。
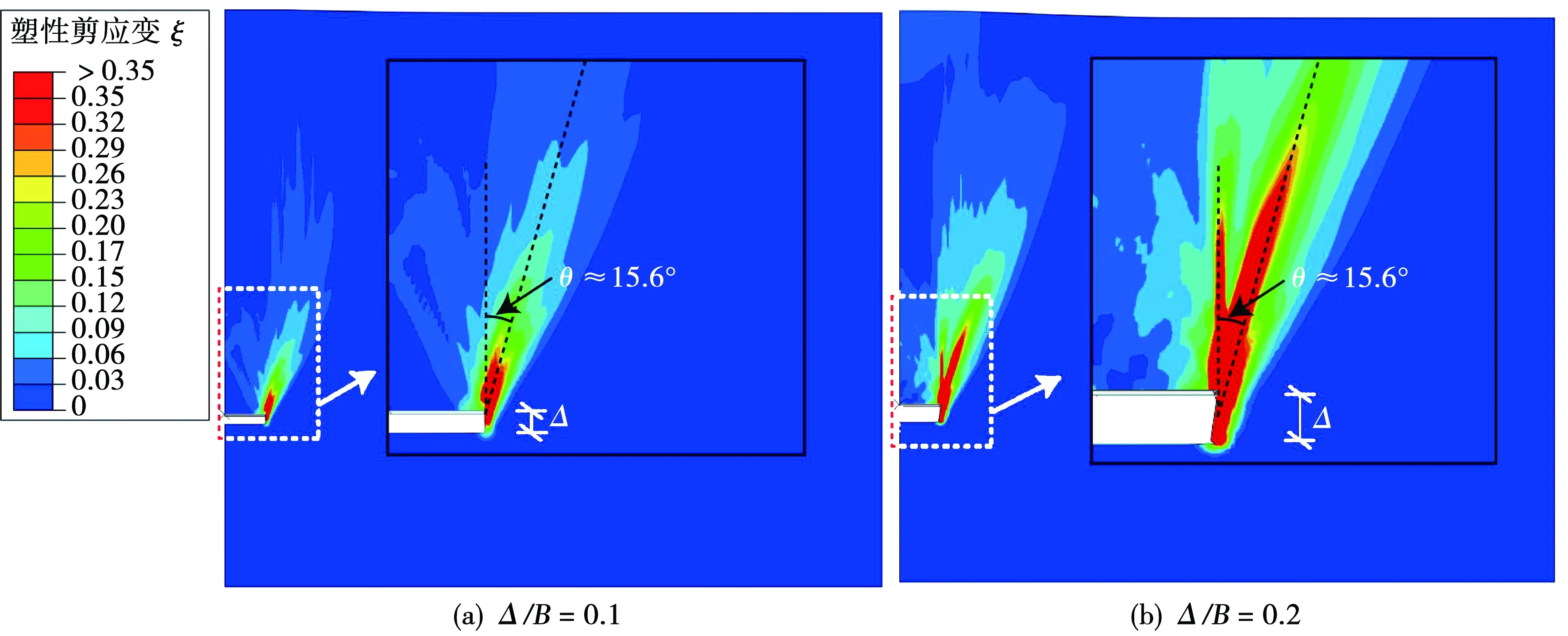
图7 平板锚基础周围的塑性剪应变变化
图8为不同位置平板锚基础周围移动摩擦角的变化。当锚板基础周围的砂土到达临界状态时,砂土的移动摩擦角减小到临界状态角(φcv=32°)。随着竖向上拔位移的增加,锚基础周围砂土的临界状态区以θ≈15.6°方向沿着砂土表面延伸。
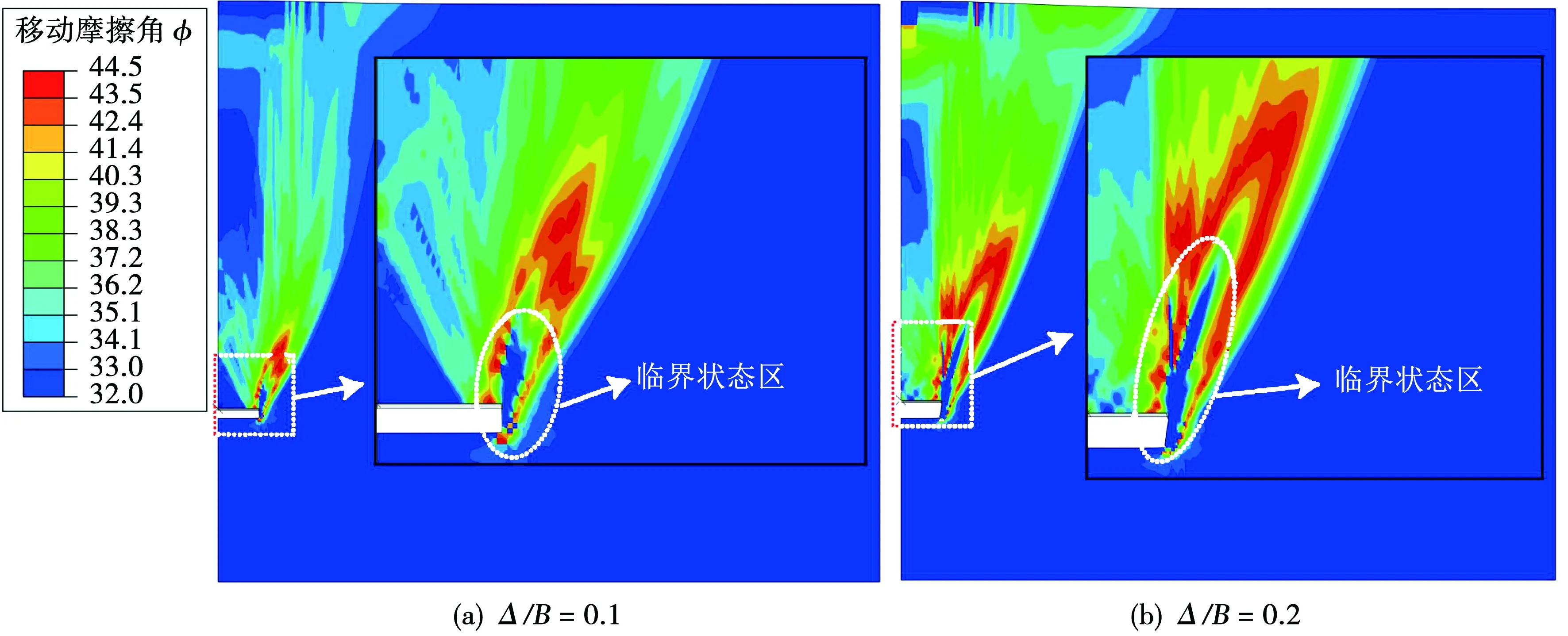
图8 平板锚基础周围的移动摩擦角变化
2.3 摩擦因数对抗拔承载力的影响
为探究锚板的摩擦因数对抗拔承载力的影响,采用表1组3算例,其中,H/B分别为3和6,μ从0变化到1.0,Dr=70%,φcv=32.0°,计算结果如图9所示。可以看出,在两组不同的埋置深度(H/B=0.3、0.6),平板锚基础的摩擦因数对抗拔承载力系数几乎没有影响。这是由于平板锚基础厚度t较小,在锚基础上拔过程中,与锚基础受到的上部砂土应力相比,基础侧壁的摩擦力对抗拔承载力的贡献可忽略不计。这与Rowe等[17]通过有限元方法计算得出的结论一致。
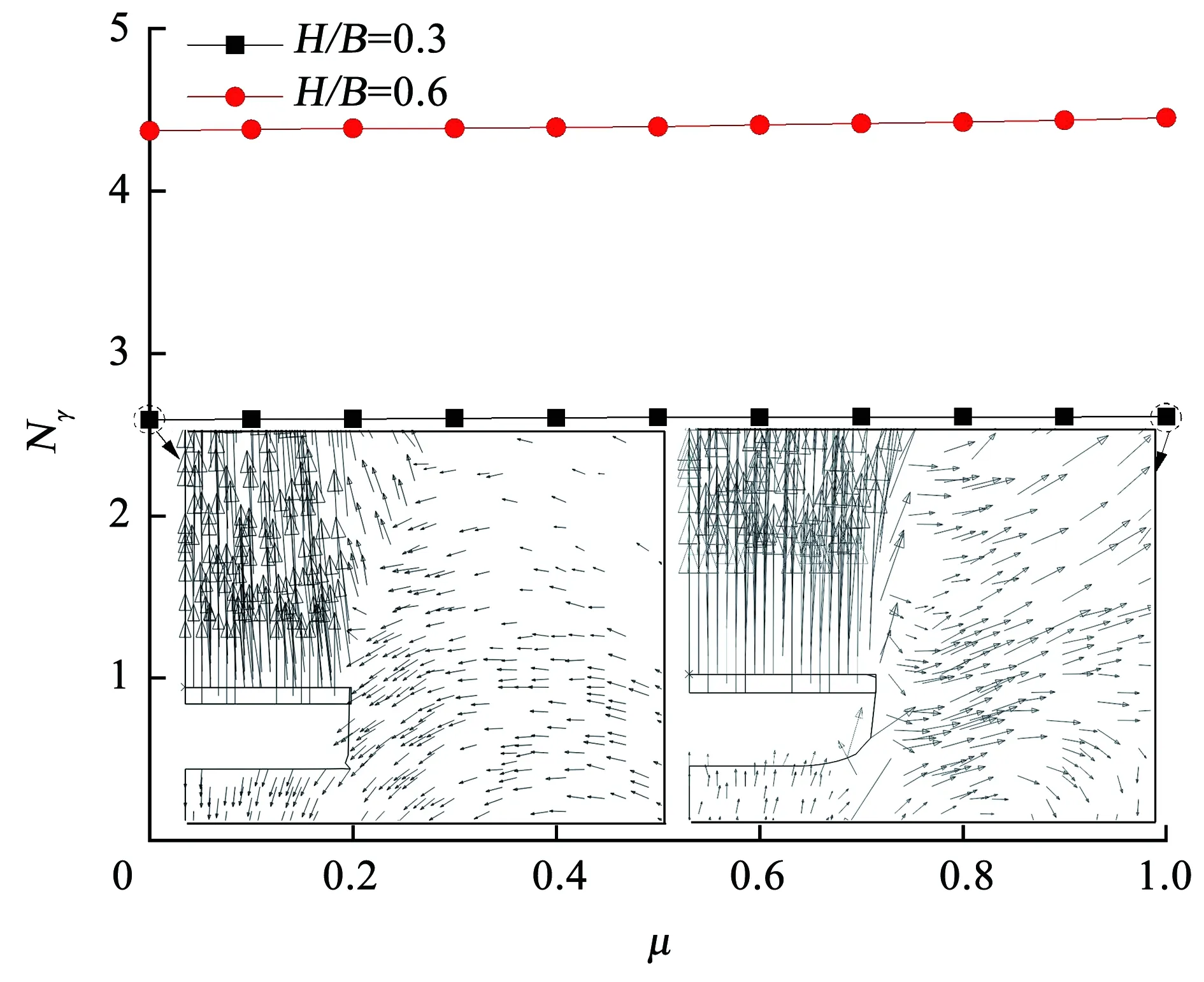
图9 摩擦因数μ对抗拔承载力的影响
2.4 砂土相对密度对抗拔承载力的影响
为探究砂土相对密度对抗拔承载力的影响,采用表1组4算例,其中,H/B分别为3和6,摩擦因数μ=0.3,砂土的相对密度Dr从10%增加到100%(松砂到致密砂),φcv=32.0°,计算结果如图10所示。可以看出,对于相同埋置深度,抗拔承载力系数Nγ随着相对密度Dr的增加而增加。在H/B分别为3和6时,Dr=100%的致密砂土中计算得到的抗拔承载力系数比松砂(Dr<33%)时承载力系数分别增加约25%和21%。
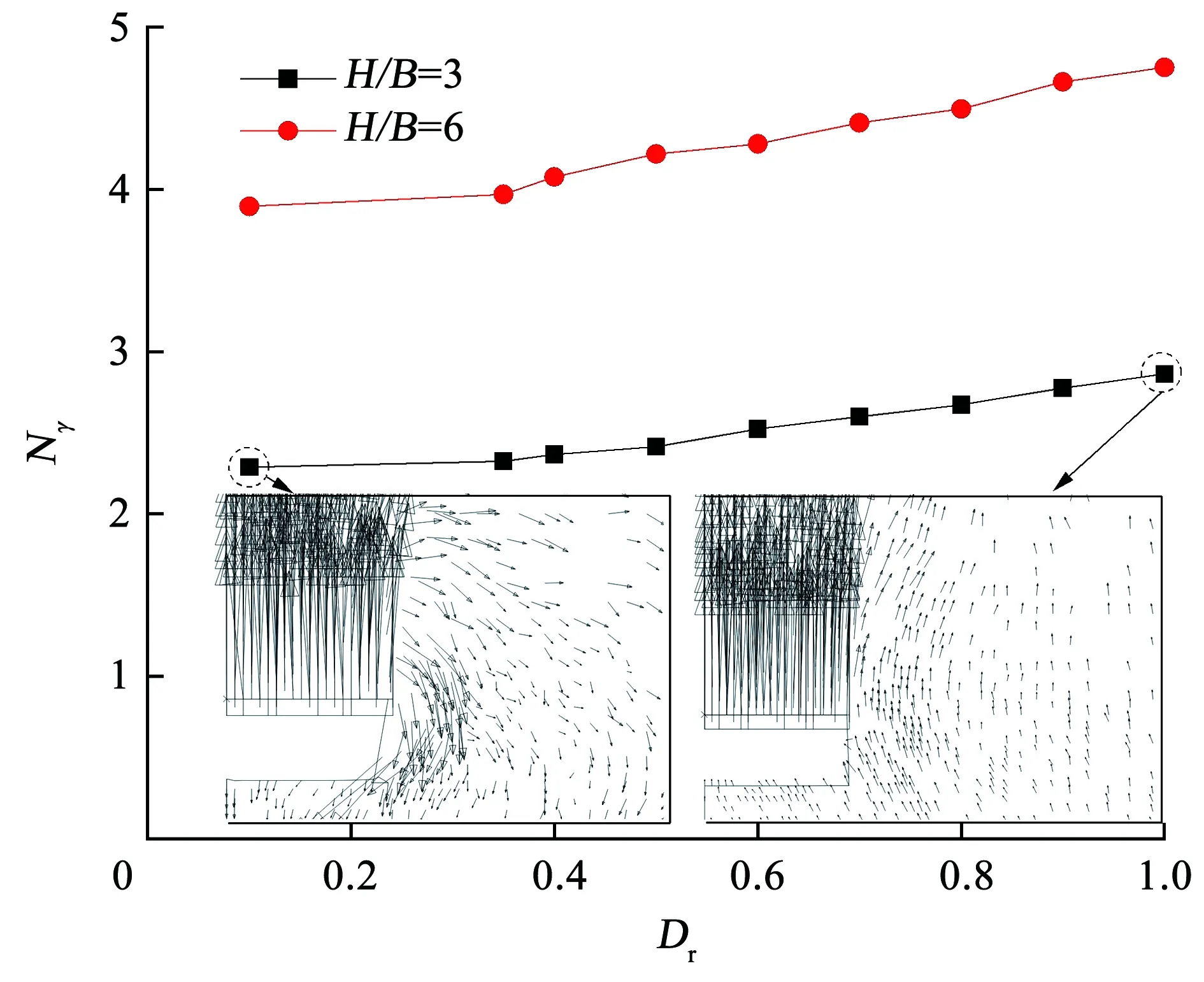
图10 相对密度Dr对抗拔承载力的影响
2.5 埋置深度对抗拔承载力的影响
为探究埋置深度对抗拔承载力的影响,采用表1组5算例,其中H/B变化范围为1.0~10,μ=0.3,Dr=70%,φcv=32.0°,计算结果如图11所示。可以看出,对于相同Dr的情况下,抗拔承载力系数Nγ随埋置深度H/B的增加而增加,这与Balla等[35]及Keskin等[36]所得的结论一致。H/B=10时承载力系数比H/B=1.0时承载力系数增加约273%,由此可见,埋置深度对抗拔承载力系数有显著的影响。另外,图11展示了根据Murray等[8]采用相关联准则(φ=φp=ψ=ψp)以及White等[12]采用非相关联准则(φ=φp,ψ=ψp)的理论计算得到的结果。对于所有的埋置深度,其理论值均高于有限元计算结果。当H/B=10时, Murray[8]和White等[12]得到的承载力系数比有限元计算结果分别高约76%和20%。
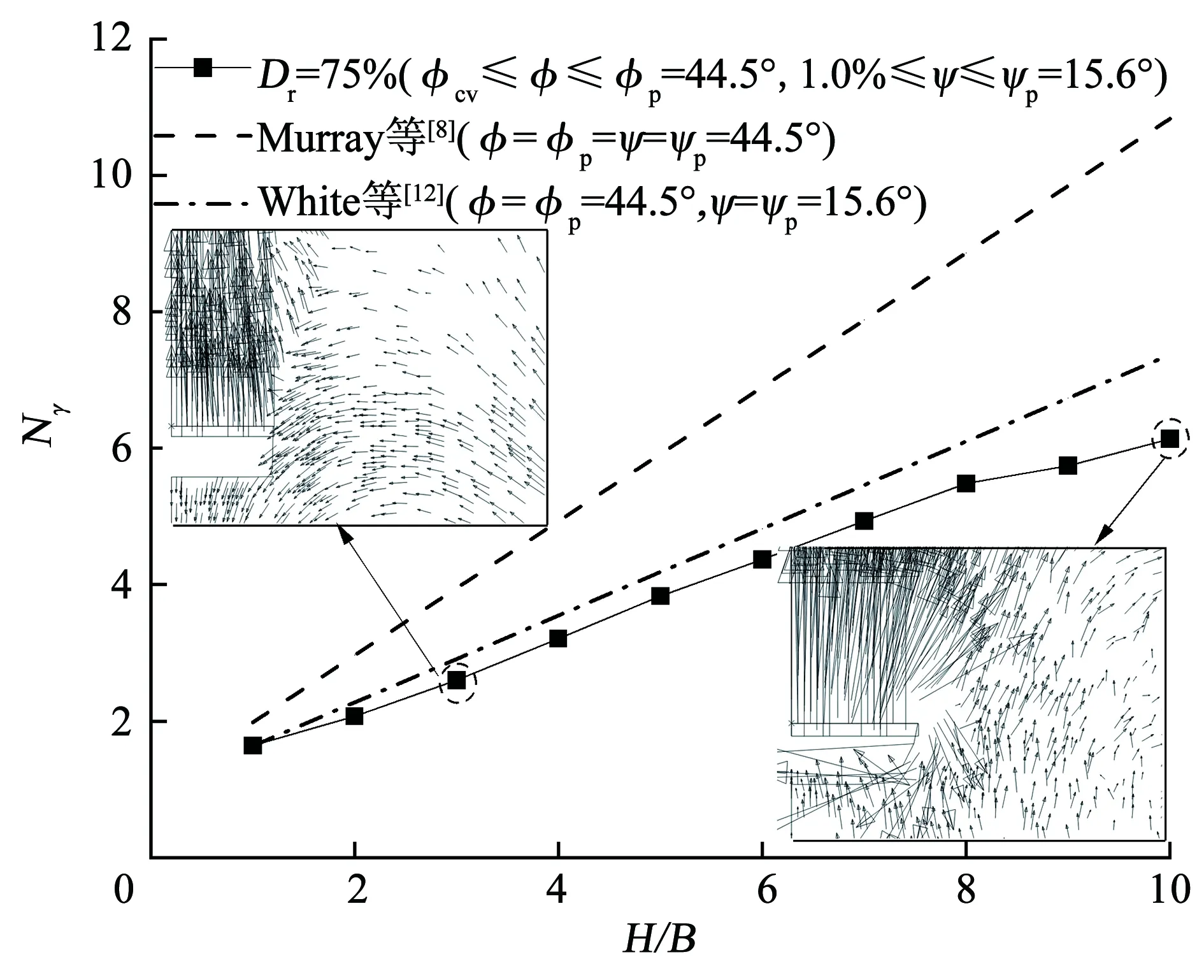
图11 埋置深度H/B对抗拔承载力的影响
3 抗拔承载力系数校准
为考察条形平板锚基础在中密及密砂中的抗拔承载力,采用算例表1组6,其中,H/B为1.0~10.0,参数Dr为40%~100%。如前文所述,条形平板锚的摩擦因数μ对抗拔承载力几乎没有影响。因此,所有算例中μ=0.3。由于砂土的临界状态摩擦角φcv主要随砂土的矿物组成及颗粒形状不同而不同[37],在本组算例中考虑φcv分别为29°,32°,35°,数值计算结果如图12所示。根据计算得到不同埋置深度以及不同砂土相对密度条件下的抗拔承载力系数,可拟合得到如下公式:
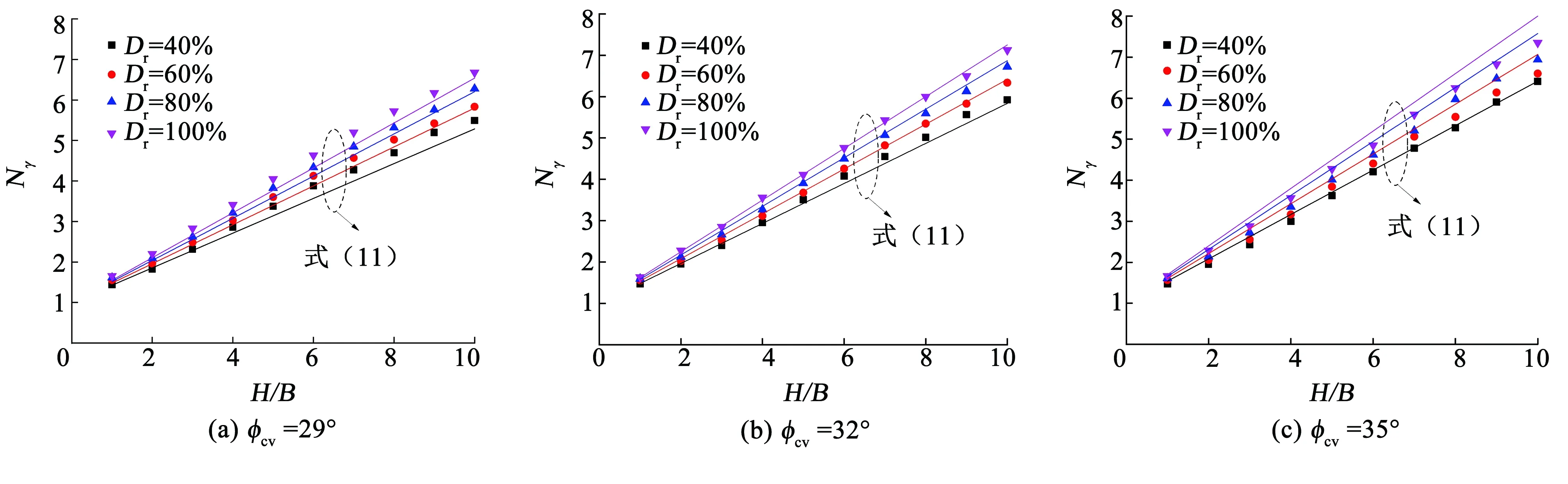
图12 抗拔承载力与Dr以及H/B的关系
(11)
其中,40%≤Dr≤100%。当Dr<33%时,抗拔承载力系数可按照White等[12]采用砂土非关联准则的等式进行计算。
4 结 论
通过二维有限元方法,采用修正Mohr-Coulomb(MMC)模型模拟平板锚在中密砂及密砂的应变软化特性,并开发相应的用户子程序,探究平板锚的抗拔承载特性。通过建立不同参数的数值模型研究锚板的埋置深度、摩擦因数和砂土的相对密度对水平条形平板锚基础在砂土地基中抗拔承载力的影响,并提出校正承载力系数公式。主要结论如下:
1)与传统的MC模型相比,MMC模型仅需3个附加参数(φini,φp,ψp)将应力和密度对砂土强度和剪胀性的影响结合起来,并对中密砂及密砂中平板锚-砂土的相互作用进行描述,提供了一种模拟砂土的硬化-软化行为的新方法。
2)平板锚的埋置深度对抗拔承载力系数有显著影响。H/B=10处承载力比H/B=1处承载力高273%。
3)砂土的相对密度越大,平板锚基础的抗拔承载力系数越大。在H/B=3处,密砂(Dr=100%)中抗拔承载力比松砂(Dr<33%)高约25%。
4)条形平板锚基础的摩擦因数对抗拔承载力几乎没有影响。
5)根据计算结果,对平板锚基础在中密及密砂地基中不同深度的抗拔承载力系数公式进行校正,为平板锚基础的应用提供了理论依据。

