快速周扫探测系统扫描平台的高精度稳定控制

张雅琼，郭建都，徐 阳，郝小健，陈光辉，周 婧，朱晶晶

（中国北方车辆研究所 信息与控制技术部，北京 100072）

引言

随着现代无人车辆和装甲车辆火控系统的发展，车载战场目标搜索设备在战场态势感知中发挥着越来越重要的作用[1]。快速周扫探测系统通过扫描平台带动红外探测器转动实现360°全景成像，系统包含的快速反射镜能够解决快速扫描成像造成的图像拖尾问题，但对扫描平台的控制精度以及稳定性提出了更高的要求。

扫描平台由水平向与垂直向惯性稳定平台系统构成，采用惯性技术进行稳定控制。目前，惯性稳定控制主要采用2种技术方案：一是采用经典控制算法，根据稳定和控制精度等因素针对性地采取不同的补偿措施提高惯性稳定系统控制性能；二是采用智能控制策略，如模糊控制、神经网络控制、遗传算法控制等[2-4]，但这些算法计算复杂，大部分研究还处于仿真实验阶段，实际系统应用很少。工程上，扫描平台的控制大多采用设计简单且稳定的传统PID控制器，但在一些对控制精度要求较高的场景，传统PID很难取得好的控制效果。分数阶微积分是关于任意阶次的微分、积分算子特征研究理论，其本质是一个数学领域的问题[5]。近年来，一些学者已经将分数阶微积分引用到控制领域，并取得了一定的效果。作为分数阶控制的重要分支，分数阶PID控制器与传统PID控制器相比增加了2个整定参数，使得控制器设计更为灵活。目前，分数阶PID在稳定平台的应用已经有许多例子，在稳定性、抗干扰性、鲁棒性、控制精度等方面有着较好的效果[6-8]。

本文以某车载动态快速周扫探测系统为背景，介绍了系统的工作原理，建立了扫描平台的数学模型，控制算法选择分数阶PID控制器。仿真与硬件实验结果表明，分数阶PID控制下的扫描平台具有超调小、抗干扰性强、稳定精度高等特点，可以保证系统获得清晰稳定的全景图像，具有较大的实际应用价值。

1 基于快速反射镜的快速扫描成像原理

快速周扫探测系统扫描成像原理如图1所示。

系统工作时，水平电机驱动转台及其上面的装置按设定转速旋转，控制快速反射镜从初始位置进行水平方向的往复摆动，其转速与转台转速同步。由图1可以看出，在探测器积分时间(曝光成像时间）内快速反射镜的反向摆速为转台转速的1/2时，系统可实现在当下视场凝视成像，同时需保证持续时间大于探测器的积分时间。当探测器完成此视场成像后，快速反射镜快速返回起始位置，再次进行反扫，实现下一视场的凝视成像。如此循环，直至完成整个360°视场全景成像。

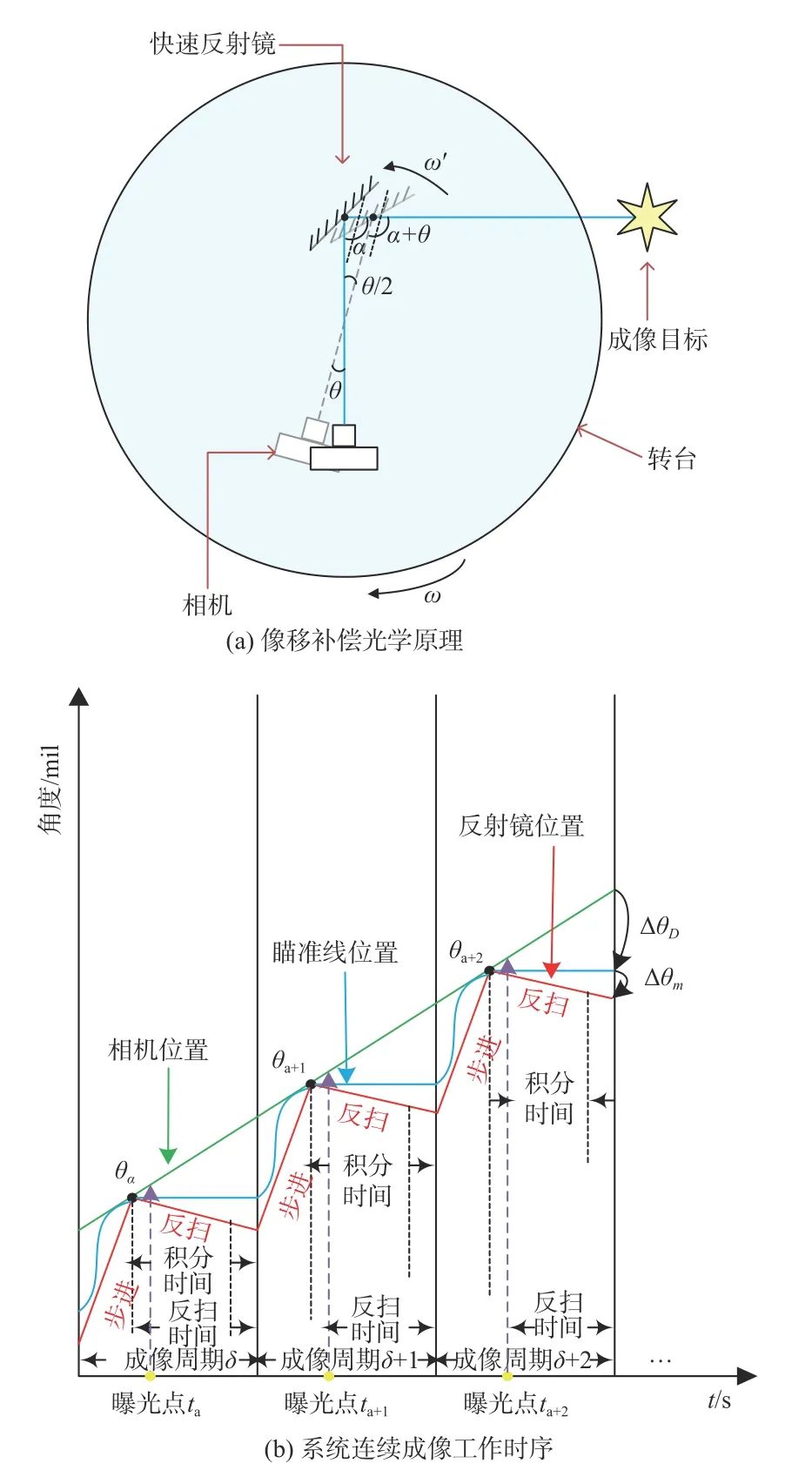
图1 快速周扫探测系统扫描成像原理Fig.1 Scanning imaging principle of fast circumferential scanning detection system

快速反射镜和扫描平台的控制是快速周扫探测控制技术的关键。由于快速反射镜固定在扫描平台上，其摆速是相对方位转台的速率，因此不受扫描平台转动的影响，且没有参数及负载变化，在曝光时间内匀速摆动可实现高精度控制。本文不考虑快速反扫镜控制系统，仅对扫描平台控制系统进行设计。

2 扫描平台控制系统建模

2.1 扫描平台控制需求分析

扫描平台控制系统的结构框图如图2所示。扫描平台控制系统包括水平向直流力矩电机、垂直向直流力矩电机、水平和垂直向功率驱动器、控制板、陀螺、编码器以及上述器件所需要的电源。

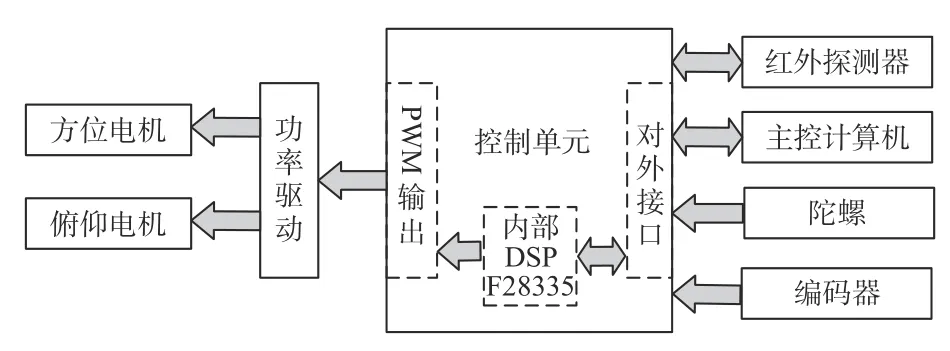
图2 扫描平台系统结构框图Fig.2 Block diagram of scanning platform control system

扫描平台主要有2个作用：一是稳定全景探测器光轴，隔离车载振动带来的干扰；二是带动探测器光轴相对大地坐标方位水平扫描。扫描平台的稳定精度直接影响成像质量，水平转台扫描速度均匀性和精度直接决定像移补偿难度。此外，由于平台内部设备的复杂性、反射镜的快速摆动及限位，使得扫描平台成为机械参数不确定和快速转矩扰动同时存在的复杂系统，传统控制算法很难实现扫描平台的高精度稳定控制。因此，扫描平台的高精度稳定控制成为快速周扫探测系统稳定成像的关键。

2.2 扫描平台工作原理及模型建立

为了满足快速周扫探测控制系统对扫描平台稳定精度和扫描速度均匀性的要求，提高系统的控制精度，建立扫描平台精确的数学模型是非常有必要的。扫描平台系统由水平和垂直2个惯性稳定系统构成，由于二者交叉耦合很小，因此暂不考虑平台耦合影响，把系统看成由彼此独立的单轴惯性稳定系统组成[9]。单轴惯性稳定平台闭环控制框图如图3所示。其中陀螺是惯性稳定平台系统中的核心部件，有干扰力矩输入时，运动载体或基座相对于惯性空间会有转动，陀螺会产生相应的角速度(或者角位移)信号，这个信号经控制器处理和功率放大器放大后传输到转台的稳定电机，稳定电机输出相应力矩驱动转台朝着相对基座转动相反方向转动，直至陀螺信号为零。当系统有信号输入时，陀螺相对惯性空间也会产生一个角速度(角位移)信号。同理，此信号也经过上述环节，使输出信号跟随输入信号变化，这种情况下陀螺仅起到一个参考基准的作用。根据单轴惯性稳定平台系统原理框图，将各个环节的传递函数带入对应环节中并简化，可以得到一个单位负反馈的惯性稳定平台控制模型。简化过程如图4所示。

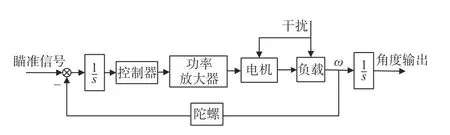
图3 单轴惯性稳平台系统闭环控制框图Fig.3 Block diagram of closed-loop control for uniaxial inertial stabilization platform system

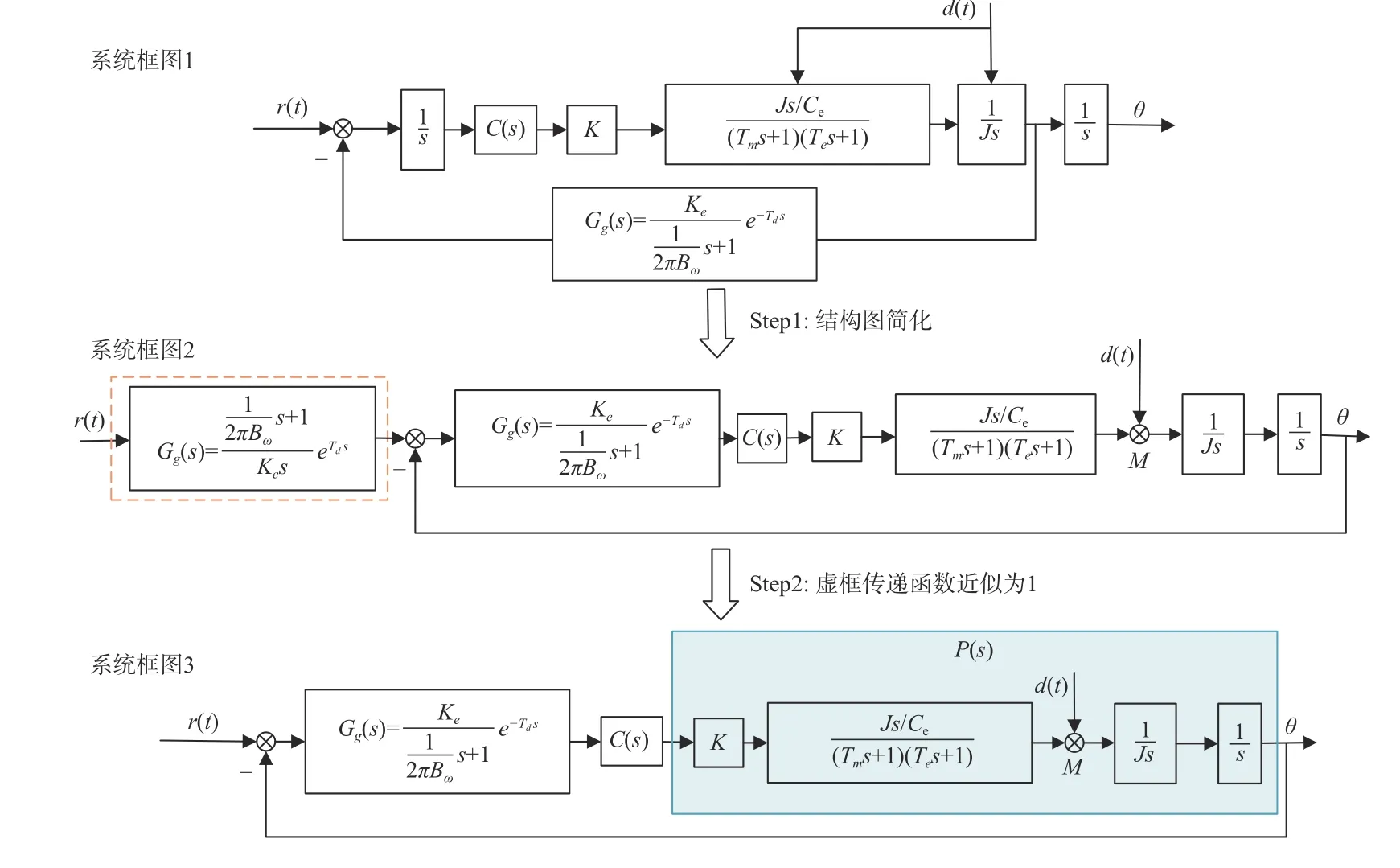
图4 惯性稳定回路数学模型简化过程Fig.4 Simplification process of mathematical model of inertial stabilization loop

3 分数阶PID控制器设计

3.1 分数阶PID控制器

由Podlubny教授提出的分数阶PID控制器——PIλDμ是传统PID控制器的一般形式[10]，其传递函数为

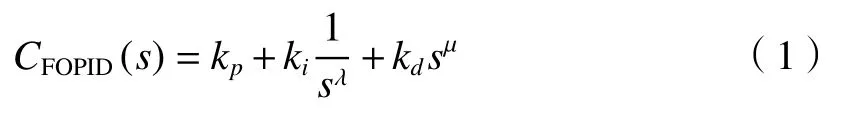
式中：kp、kd、ki是PID控制器的整定参数；s表示原函数经过拉普拉斯变换后的表达式；积分项阶次λ和微分项阶次 μ理论上可以是任意实数。若λ≥2，μ≥2，则控制器采用与传统PID控制器不同的高阶结构[11]。

图5是分数阶PID示意图，横纵轴分别为积分阶次 λ和微分阶次μ。由图5可以看出，传统PI、PD、PID控制器只是等价于图上离散的几个点。由于引入了2个附加的整定参数 λ 和μ，则控制器参数的调整将更加灵活，在某些控制问题中分数阶PID控制器的性能优于传统PID控制器[12]。

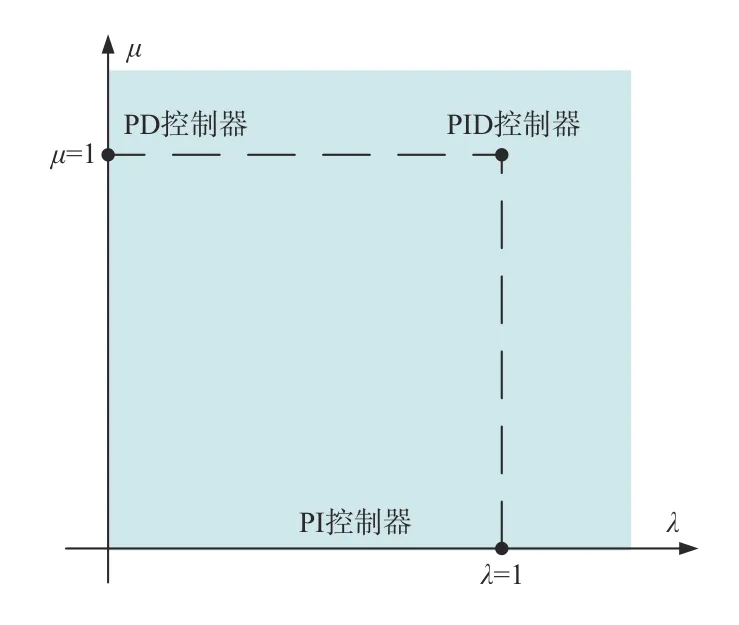
图5 分数阶PID 示意图Fig.5 Schematic diagram of fractional-order PID

3.2 控制器设计

表1为某车载快速周扫探测系统水平向和垂直向惯性稳定平台参数。将表1内参数带入图4所示惯性稳定平台的数学模型中，可以得到水平向和垂直向的被控对象，即给定电机位置系统P(s)。其中，

空间自相关分析基于相关指标来测度要素在空间分布上是否呈现聚集性从全域空间自相关、局部空间自相关两个方面进行分析。

表1 水平向与垂直向惯性稳定平台参数Table 1 Parameters of horizontal and vertical inertial stabilization platform

水平向被控对象：

垂直向被控对象：

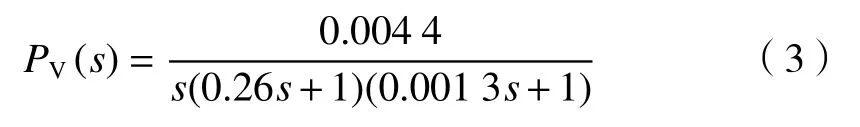
利用文献[13]提出的基于内模控制的分数阶PID设计方法，分别设计水平向和垂直向的分数阶PID控制器。

给定穿越频率ωc=340rad/s 和相位裕度φm=50，得到水平向分数阶PID传递函数：

给定穿越频率ωc=370rad/s 和相位裕度φm=50，得到垂直向分数阶PID传递函数：

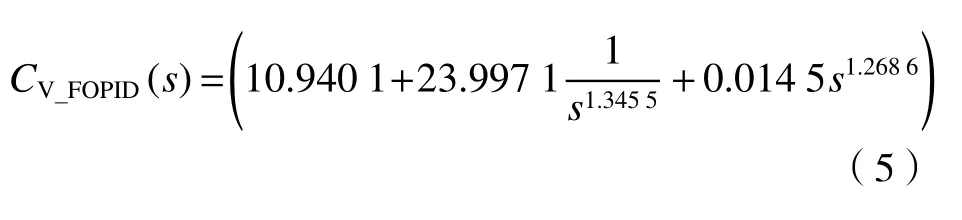
在扫描平台上可验证分数阶PID控制策略的有效性，并与传统PID的控制性能进行仿真和实验对比。为了突出算法的可比性，传统PID控制器的设计仍延用文献[13]中提到的频率约束法，得到水平向和垂直向PID控制器的传递函数为

水平向：

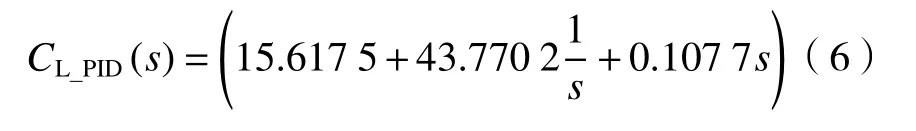
垂直向：

4 仿真与实验结果

在Simulink中搭建的仿真平台如图6所示。其中惯性稳定平台采用连续系统建模，控制器采用离散系统建模。

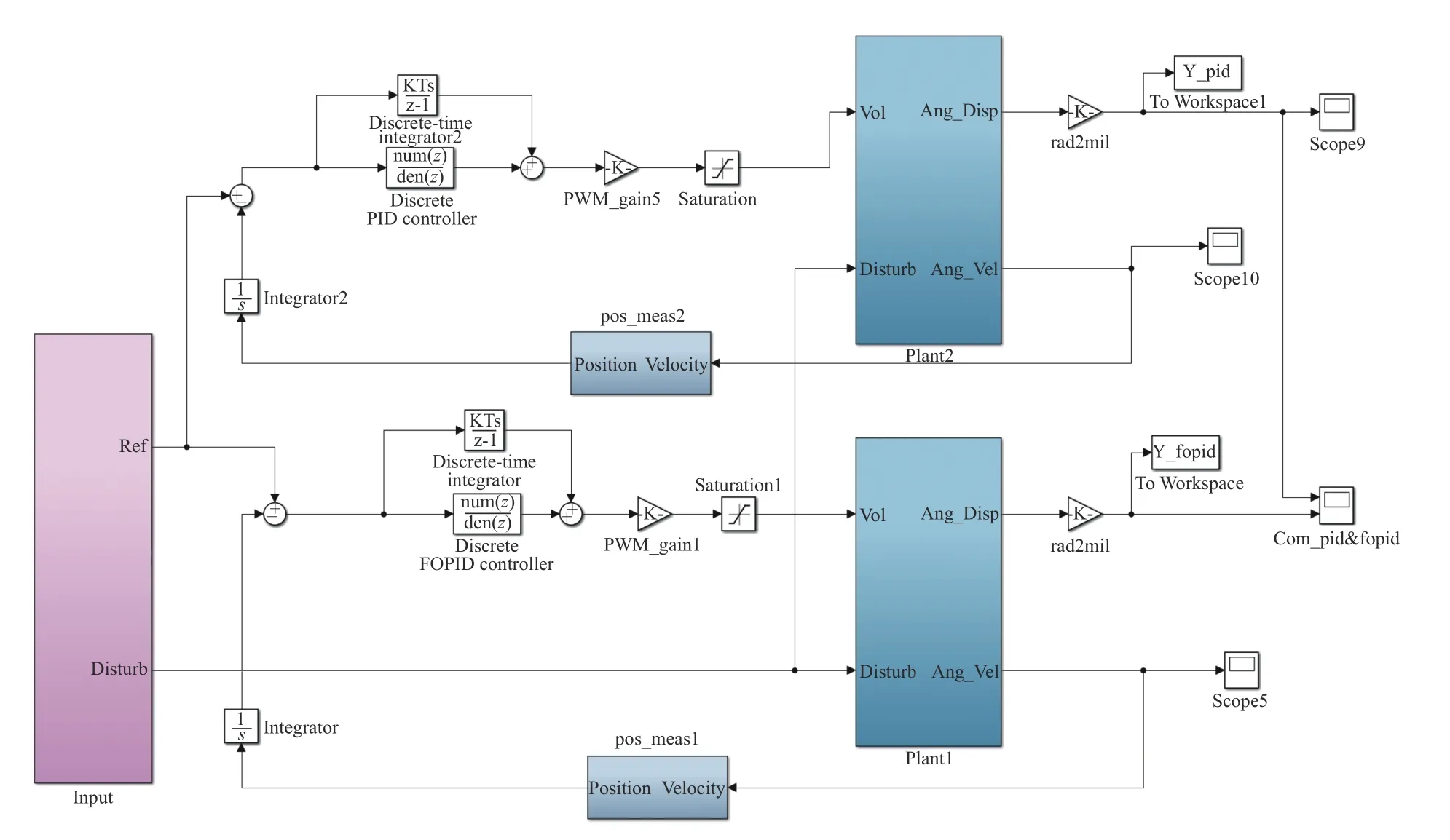
图6 单轴扫描平台的Simulink仿真模型Fig.6 Simulink simulation model of uniaxial scanning platform

快速周扫探测控制系统硬件实验平台如图7所示。其中控制主板处理器为TMS320F28335，最高频率为150 MHz[14]，仿真和实验中算法的采样率均为4 kHz。为了平衡控制算法的运算精度和时间，同时考虑实际硬件平台控制DSP芯片(TMS320F28335)的运算速度和存储空间等因素，离散后控制器系数精度取到小数点后3位。水平向分数阶PID控制器选取幂级数展开法[15],；垂直向分数阶PID控制器选取Muir递归法[16]，得到水平向和垂直向的离散控制器模型为

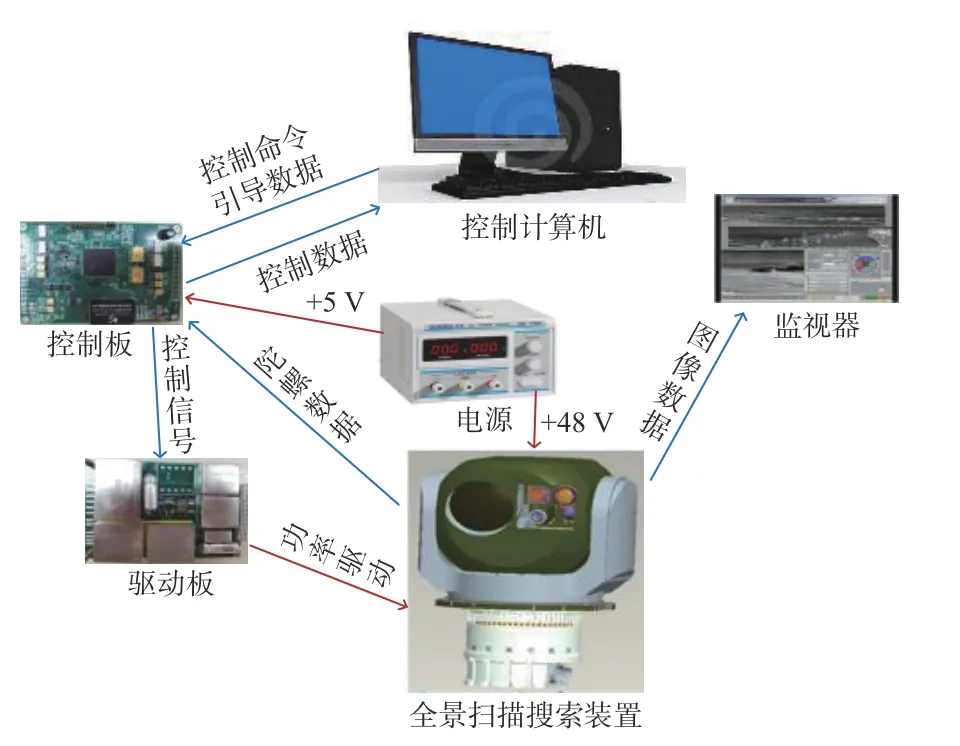
图7 快速周扫探测控制系统现场实验装置Fig.7 Composition of field experiment of fast circumferential scanning detection and control system

水平向分数阶PID控制器（幂级数展开法）：

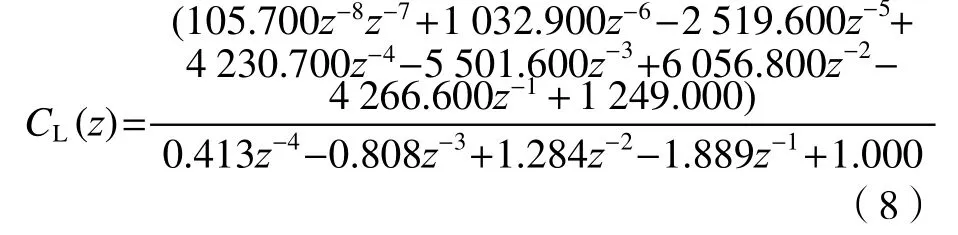
垂直向分数阶PID控制器（Muir递归法）：

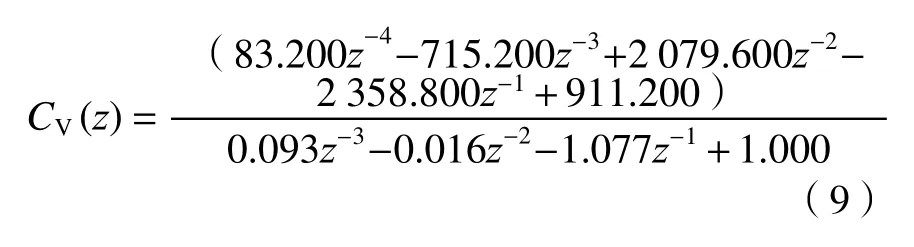
4.1 仿真结果

仿真中扫描平台的水平向转台转速参考值设定为 ω =144/s，图8为PID和分数阶PID控制下的系统转速响应结果。从图8转速放大图中可以看出，分数阶PID算法的转速响应精度高于PID控制器。

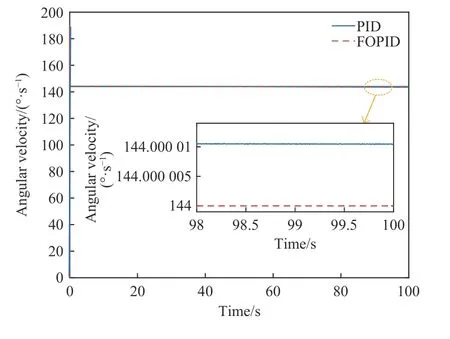
图8 水平向转台控制系统转速响应Fig.8 Speed response of horizontal turntable control system

图9为扫描平台的水平和垂直转台在给定输入 r (t)=60时转台位置阶跃响应。从图9中可以看出，分数阶PID控制下的系统阶跃响应最快，调节时间短且稳定无超调。

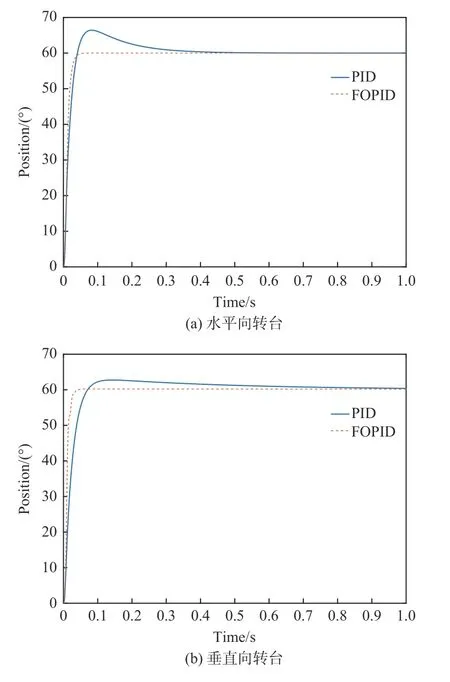
图9 转台控制系统位置响应Fig.9 Position response of turntable control system

在图4 中M处加一正弦干扰力矩d(t)=0.005×sin(4πt)，转台位置扰动输出如图10所示。通过图10可看出，无论分数阶PID还是PID，位置响应均呈现出同频率的起伏变化，但分数阶PID起伏明显小于PID控制器，这说明分数阶PID控制下的系统抗干扰性能、稳定性更高。

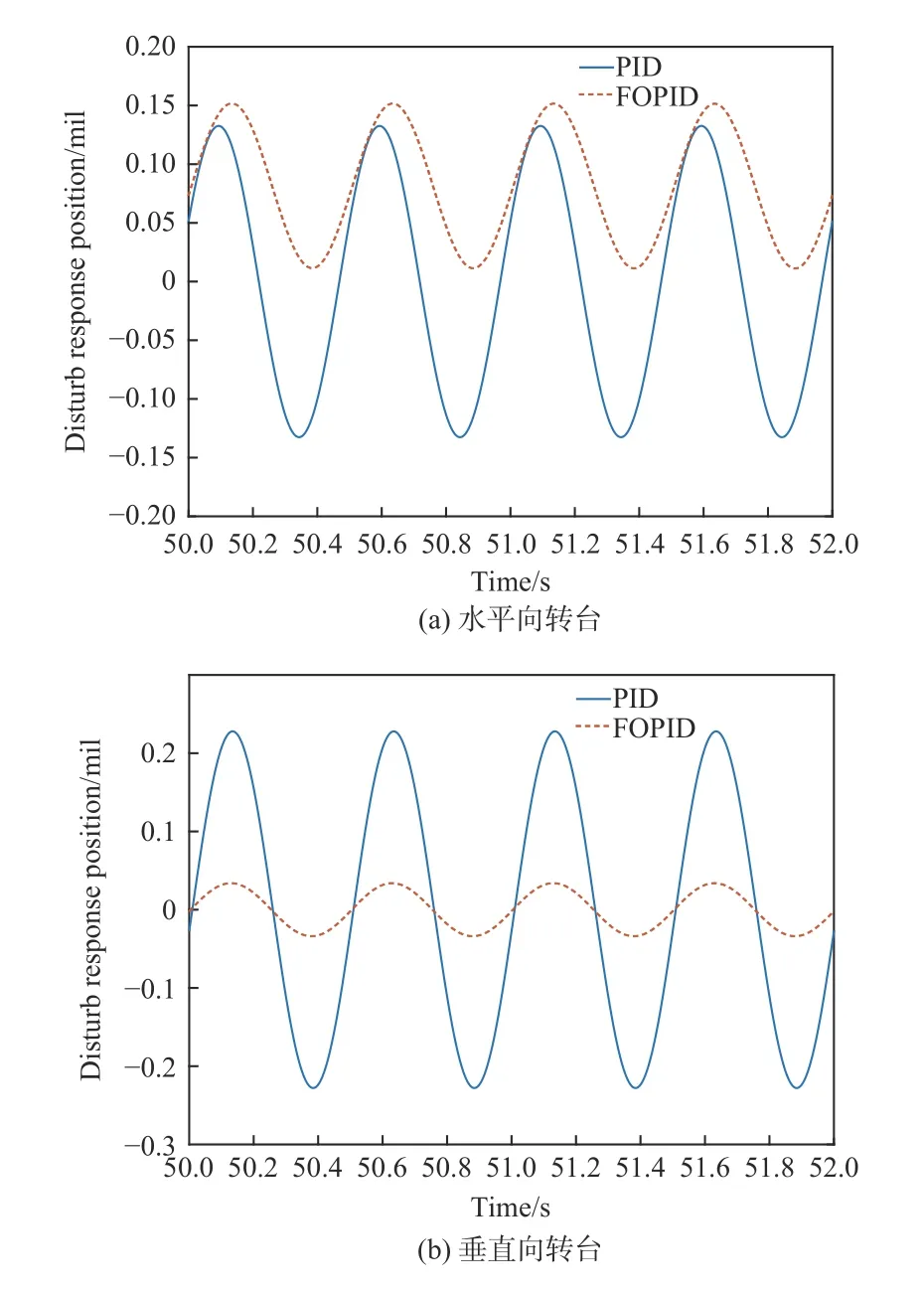
图10 转台控制系统扰动位置输出Fig.10 Disturbance position output of turntable control system

4.2 硬件实验结果

实验时在CCS实验平台完成对控制参数在线更改以及实验数据采集。通过CCS画图工具Tools→Graph画出响应曲线，其中数据采集频率为1 kHz，纵轴每个单位代表0.002 mil（即0.000 12°）。扫描平台由水平向方位转台与垂直向俯仰转台构成，下面分别对方位转台与俯仰转台的控制性能展开讨论。

给定转速信号为144°/s，传统PID和分数阶PID控制下系统的转速响应调试截图如图11所示。通过图11对比可以看出，分数阶PID控制下,系统的稳态精度达到了0.41%，高于PID控制下系统的0.76%，表明转台的扫描速度更为均匀，更利于配合快速反扫镜扫描成像。

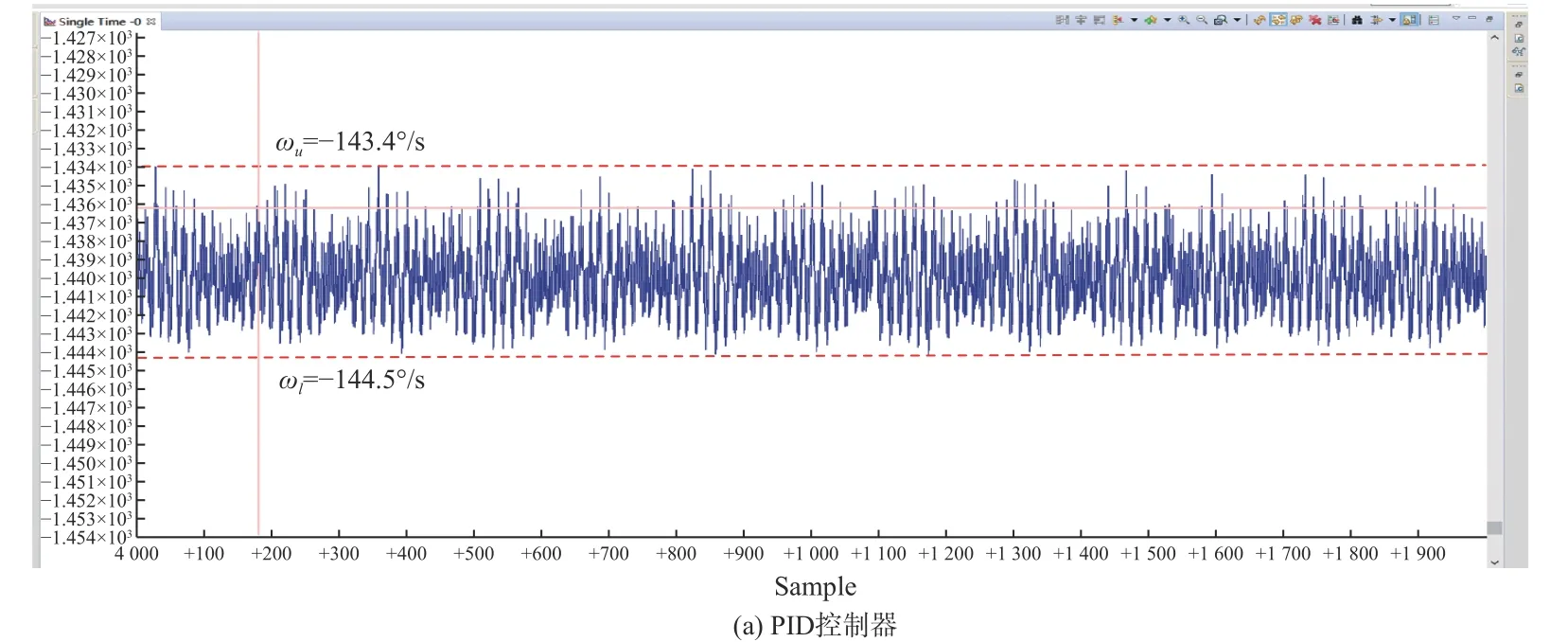
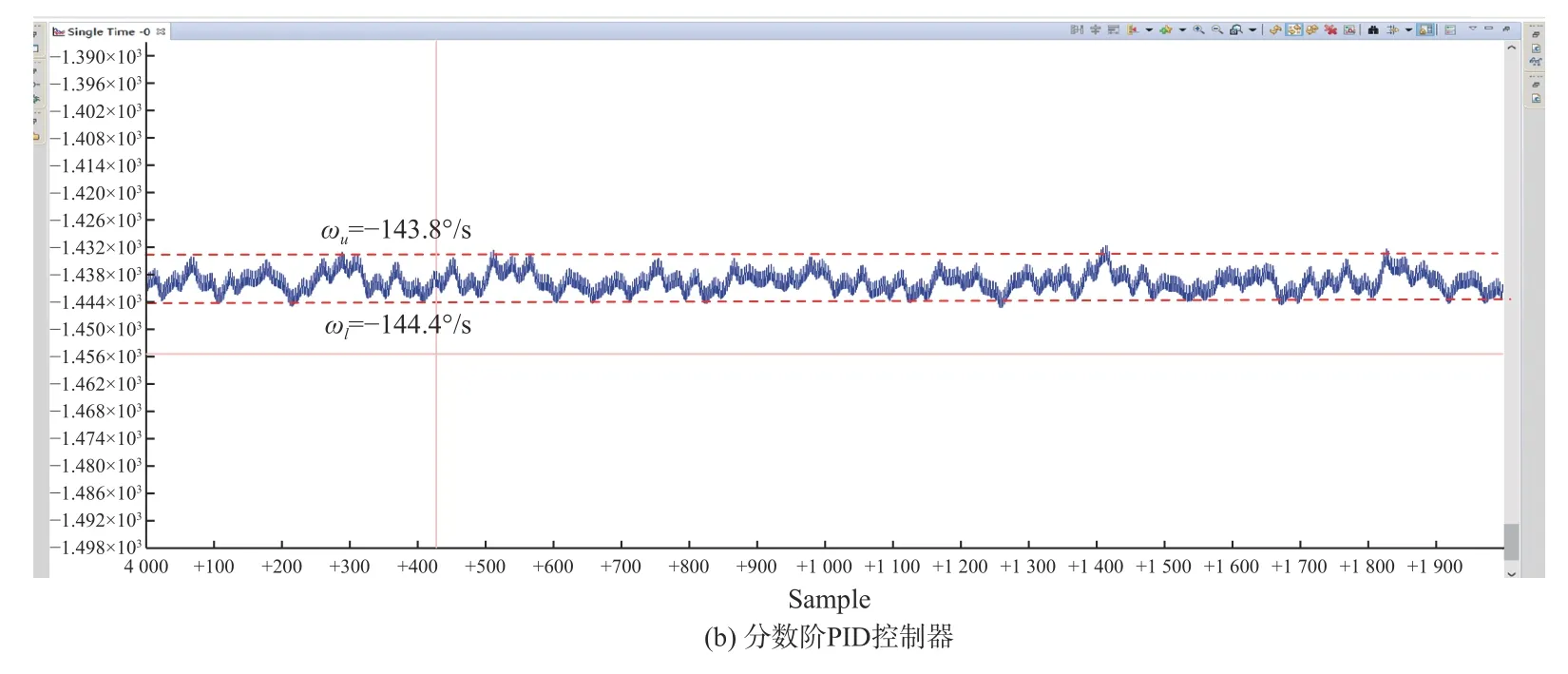
图11 水平向转台控制系统速度响应曲线Fig.11 Speed response curves of horizontal turntable control system

在实际快速周扫探测系统运行时，系统跟瞄控制表示从某一个位置快速精确地运行到另一个位置，是系统的一项重要指标，可以通过给定阶跃信号分析控制系统的动态效果。给定阶跃输入10°，快速周扫探测系统的位置阶跃响应如图12和图13所示。从图12和图13可以看出，无论是水平向转台还是垂直向转台，分数阶PID控制器均具备更好的控制效果。

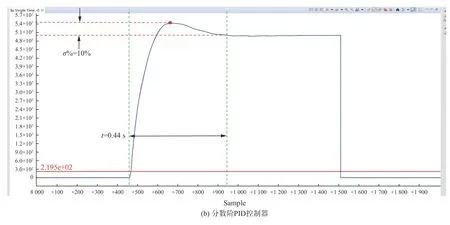
图12 水平向转台控制系统位置响应曲线Fig.12 Position response curves of horizontal turntable control system

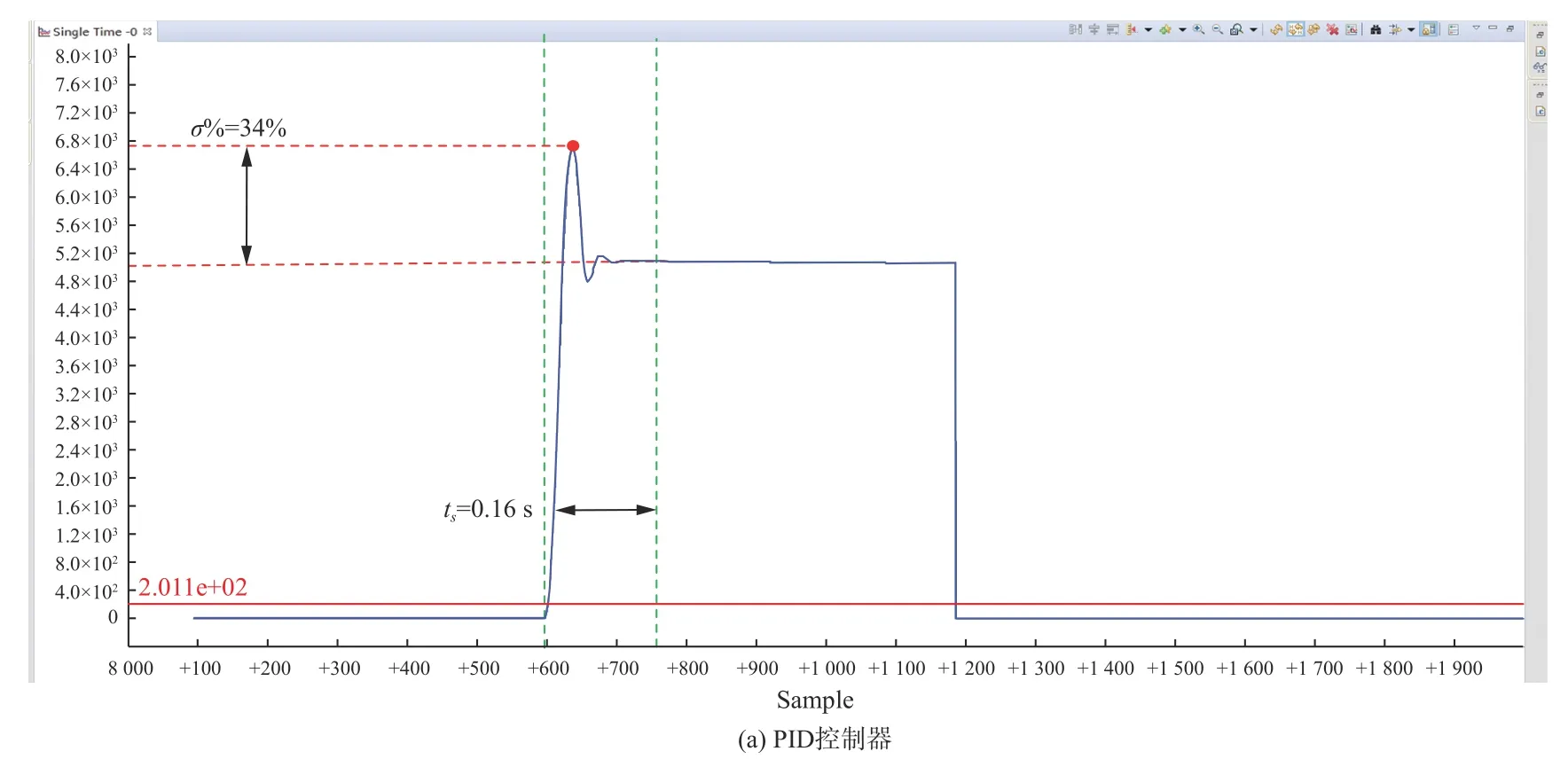
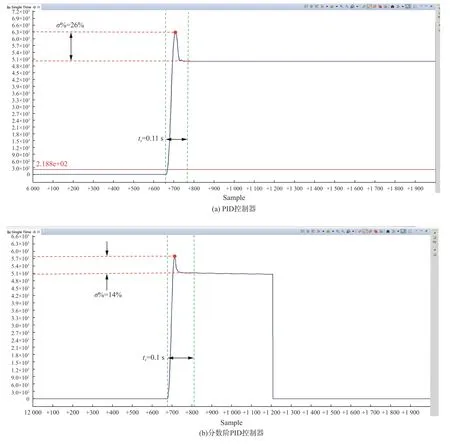
图13 垂直向转台控制系统位置响应曲线Fig.13 Position response curves of vertical turntable control system

给定扰动信号为幅值3°，频率为2 Hz的正弦信号，通过采集陀螺速度信号积分后可测试系统的抗干扰性，图14和图15是水平向和垂直向转台的扰动位置响应输出。由图14可求得水平向转台PID稳定精度为0.005 82°(1σ)，分数阶PID稳定精度为0.001 26°(1σ)。同理，由图15可求得垂直转台PID稳定精度为0.003 66°(1σ)，分数阶PID稳定精度为0.001 62°(1σ)。说明分数阶 PID 控制对系统抗干扰性能提升是显著的，系统可以获得更好的稳定性。

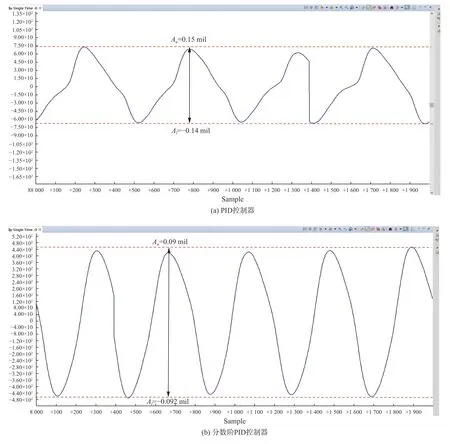
图14 水平向转台控制系统扰动位置输出Fig.14 Disturbance position output curves of horizontal turntable control system

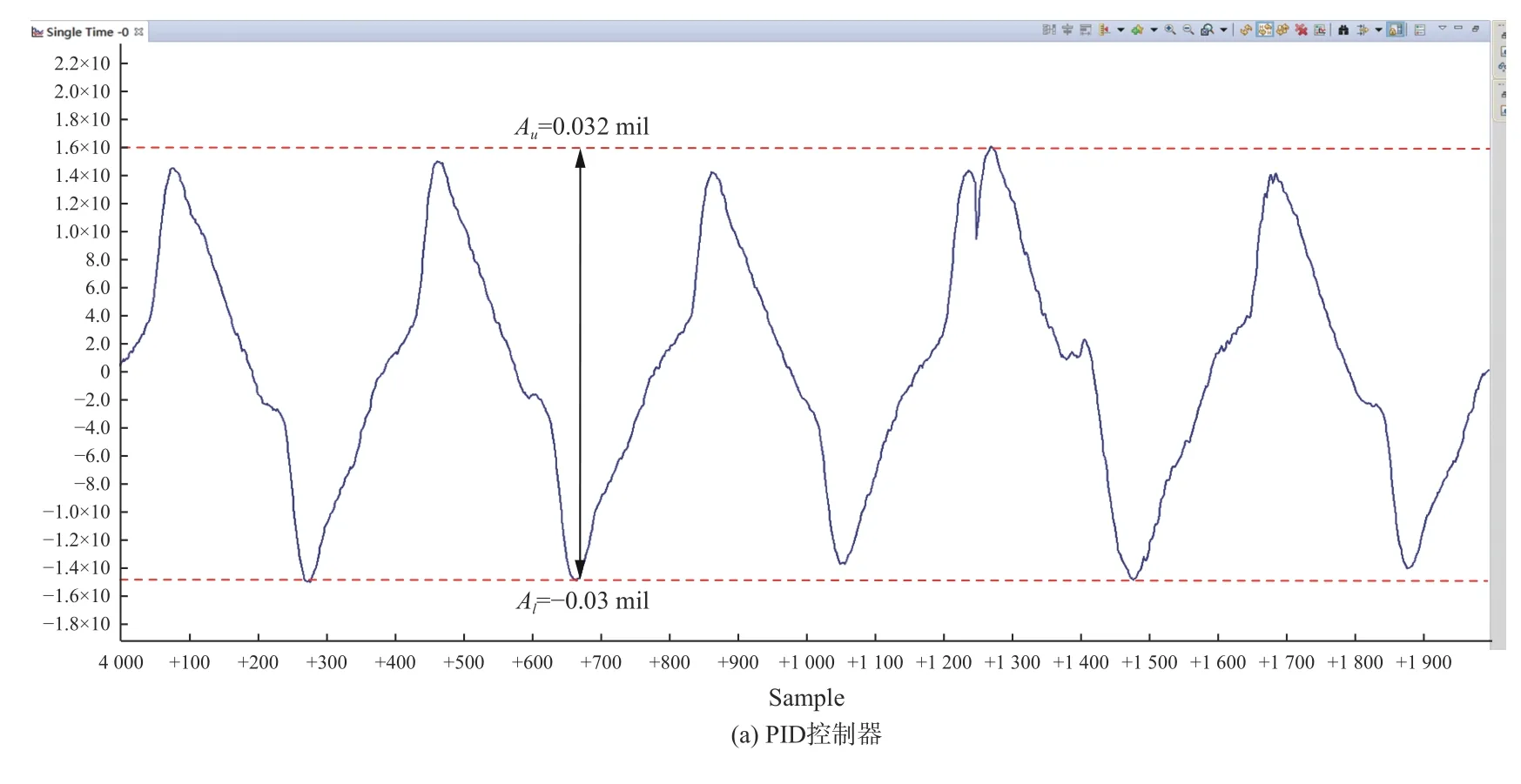
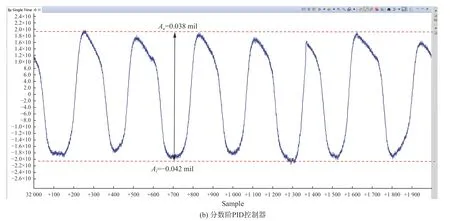
图15 垂直向转台控制系统扰动位置输出Fig.15 Disturbance position output curves of vertical turntable control system

最后，利用分数阶PID控制算法对原理样机进行控制，并对周围360°空间场景进行实景成像。系统搭载红外探测器参数为：单帧水平视场角为9°、单帧像素为1 024×1 280像素、曝光时间为10 ms、帧频为16 Hz，转台转速设定为144°/s(快速反射镜匀速段摆速设定为72°/s)。系统所成单帧图像经处理拼接后得到如图16所示(限于图像长度，将全景图像拆分为4部分展示)周视全景成像图，图17为其局部放大图。从图16和图17可以看出，系统360°全景范围内图像清晰稳定，分数阶PID控制下扫描平台得到了很好控制。

图16 快速周扫探测系统360°全景成像图Fig.16 360° panoramic imaging images of fast circumferential scanning detection system

图17 全景成像局部放大图Fig.17 Partial enlarged images of panoramic imaging

5 结论

通过对快速周扫探测系统中快速扫描原理进行介绍，指出对扫描平台的控制是系统清晰稳定成像的关键，围绕提高扫描平台的控制精度、抗干扰性以及稳定性等问题展开了研究。根据扫描平台控制原理建立了双向惯性稳定平台模型，基于该模型设计并实现了分数阶PID控制器。仿真和硬件实验数据均表明，分数阶PID在控制精度和抗扰动能力方面比传统PID具有明显优势。在实验所用快速周扫探测系统平台下，水平向转台转速设定在144 °/s时，系统全景成像清晰稳定，具有较高的实用价值。