毫米级弹性散射子半径的超声定量检测

张雅婧，张鸿博，王铭浩，莫润阳

(1.陕西师范大学 超声学重点实验室，西安 710119；2.石油管工程技术研究院，西安 710077)

散射体的超声无损定量，无论在工业生产过程中的质量控制还是在医学诊断治疗领域都有着广泛的应用需求。在工业生产领域中，对结构微缺陷的检测及定量是结构健康监测和容限寿命评估的基础；在医学诊疗领域中，生物组织可建模为一系列散射声波的微小粒子的组合[1]，如各种血液细胞及血管内皮细胞受到刺激而活化或发生凋亡后，细胞膜磷脂酰丝氨酸由细胞膜内层进入外层，以出芽方式形成小泡状结构脱落产生的微粒，是病情监测、指导治疗及疗效诊断的散射源[2]。对微缺陷、微粒子等散射子的大小、分布及运动速度等参数进行定量检测，涉及其在各领域的应用，是对其进行效果评价的重要内容。

对尺度与波长相当或小于波长的散射体进行定量检测主要基于光、声两类能量形式。光学方法一般适用于透明液体，如高速摄影、Mie散射[3]等。在微泡尺度及弹性的定征方面，光学技术已成功应用多年[4]，然而对于血液、磁流体甚至固体金属等不透明液体或固体中的微散射体，超声检测则是最具前景的定征工具。声散射是超声目标定征的根本，散射声场是入射声波与散射体相互作用的结果，包含了散射体尺寸在内的许多信息。目标强度TS是表征散射体反射能力的物理量，常用于水下目标的测量，如鱼体长度评估、潜艇成像[5]等。

利用目标强度对毫米级尺度球形散射体的半径a进行定量检测，存在的最大问题是由于声波的干涉效应，两者间并非单值对应关系。为此，笔者从弹性球的声散射出发，利用差频叠加方法减弱干涉，构建TS与球体半径a之间单值对应关系，并设计试验验证了该方法的可行性。

1 弹性球回波分析数学模型

弹性球回波分析数学模型包含背散射形态函数f∞(π)和目标强度TS。若以球形微泡(粒)为检测目标，则f∞(π)和TS分别是散射场的频率响应函数和描述目标反射能力的物理量，均与目标的散射特性有关。笔者在散射声场简正级数解的基础上得到了f∞(π)，借助f∞(π)建立TS与球体半径a之间的数学联系。

1.1 散射声场及其简正级数解

将由拉梅常数为λe、μe的各向同性材料组成、半径为a的光滑弹性球置于无限大理想流体水中，设有一平面声波沿z轴入射到球上，其中ω为入射声波的角频率，k为水中的波数，c为水中声速。为计算弹性球外M点的散射声场，以球心O为坐标原点建立图1所示的球坐标系，图中r、θ和φ为球坐标系中M点的坐标变量。

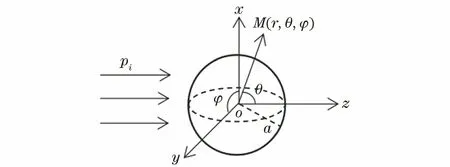
图1 弹性球及入射平面波示意

省略时间因子e-iωt，入射平面声波pi可展开为

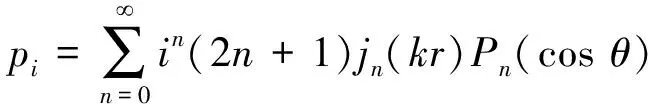
(1)

式中：n为阶数；p0为入射声压幅值；jn(kr)为贝塞尔函数；Pn(cosθ)为勒让德函数。

由于入射声波能透入弹性球内部并激发球内声场，因而球内和球外液体中都有声场，球外的散射声波ps可表示为

(2)

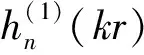
1.2 背散射波的形态函数和目标强度

形态函数f∞是描述目标体散射特性的物理量，与入射声波频率、目标大小和组成材料的特性有关，其定义为[6]

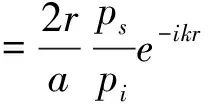
(3)

当观测角θ=π时，可得背散射波的形态函数模|f∞(π)|为

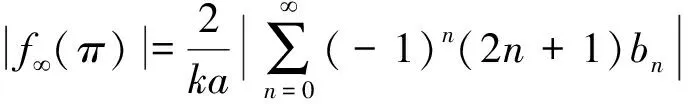
(4)

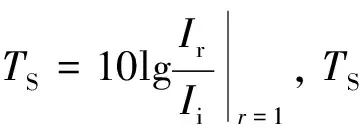
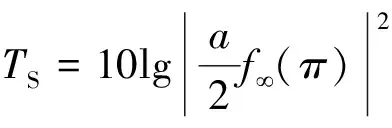
(5)

式(5)即为由TS定量散射子半径a的理论依据。

2 数值结果及讨论

对铜、铝及碳钢三种弹性球散射波形态函数进行数值计算，并分析TS与a的关系及材料特性的影响。数值计算中，水中声速为1 500 m/s，铜、铝及碳钢中横波声速依次为1 940，3 040，3 230 m/s。

2.1 形态函数

铜、铝和碳钢三种材料弹性球背散射波的形态函数如图2所示，作为对比，图中红色虚线为刚性球的|f∞(π)|。由图2可见，弹性球形态函数随ka的振荡起伏较刚性球的更为剧烈，对频率的依赖更强。其根本原因为材料弹性所致的内部共振[6]，ROBERT[7]认为，共振峰的间隔主要与横波波速cT正相关，cT越小峰值间隔越小。图2中横波声速最小的铜球共振峰最大且在相同的ka区间的共振峰个数最多，与此结论一致。

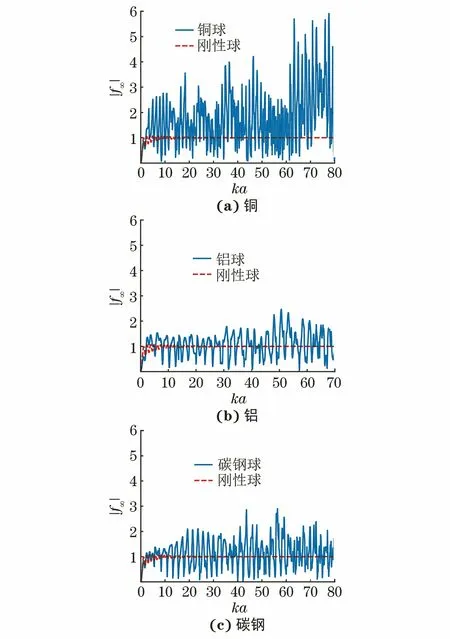
图2 弹性球背散射波的形态函数

2.2 目标强度

以形态函数为基础，由式(5)计算平面波入射时弹性微球的TS。入射声波频率f为2.5 MHz，在相同接收位置处，三种材料弹性球的TS-a关系曲线如图3所示。总体上看，散射强度随球半径a增大而增大，但这种关系带有相干信息，单调变化的曲线伴随有局部峰值，这意味着每个a都与一个TS单值对应，但相同的TS可能与多个a对应。这种多值性在物理上是可以理解的，这是由于平面波经球散射后分成多束相干波，一个处于差的相干态的大散射体所产生的声强，可能不及处于好的相干态的小散射体[3]。这种多值问题虽然容易理解，但却使基于目标强度TS确定散射体尺度a的方法面临困难。

值得一提的是，图3中三条曲线上TS的波动范围大致相同，第一个极大值对应的a几乎相同，说明材料差异对TS的贡献可忽略。对图3(c)曲线的上OA段局部放大发现, 该段曲线光滑几乎没有凸起，说明此时散射干涉影响微弱，TS与a具有单值对应特性，存在由TS唯一确定a的可能性。然而，此时水中波长λ约为0.6 mm(f=2.5 MHz), 而图3中OA段对应a的极大值仅为0.12 mm，λ≫a，这对换能器来说是难以分辨的，不仅如此，此时球的TS值极其微小，在OA段内对a定量极为困难。虽然徐盛瀛等[8]采用了声学隧道效应来增强目标强度，但该技术仅适用于低频范围。总之，需要对OA段以外的部分设法减弱或消除干涉，使TS与a产生单值对应性，是通过测量散射体目标强度获得其半径的根本。所幸的是，目标强度TS是f∞(π)的函数，f∞(π)的频率依赖性使得TS也具有频率依赖性，这为消除干涉提供了条件。

图3 三种材料弹性球的TS-a关系曲线

2.3 TS-a单值化方法-差频叠加处理

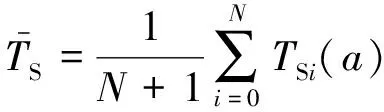
(6)

以此均值作为散射球体的最终目标强度，可减弱干涉效应，使曲线平滑。

设探头中心频率为2.5 MHz，3 dB带宽为1.75 MHz～3.25 MHz，当Δf分别取500，150，20 kHz时，碳钢球散射目标强度叠加效果如图4所示。与单频(f=2.5 MHz)效果相比，差频叠加后曲线起伏程度明显减弱，从曲线平滑效果来看，Δf=20 kHz时最好，Δf=150 kHz时次之，Δf=500 kHz时最差，当Δf取值为20 kHz时曲线上的凸起几乎完全被平滑，此时TS-a关系在一定精度上可认为具有良好的单值对应性。但并不是Δf越小，平滑效果越好，若继续减小Δf，曲线的平滑程度不会有更大改善，反而令大大延长计算时间。因此，进行差频叠加时Δf的取值应兼顾频带范围及测量精度。

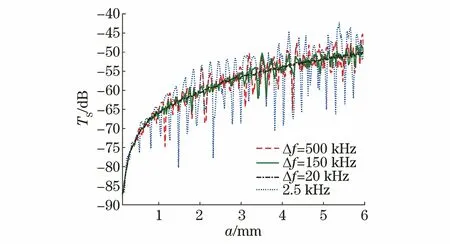
图4 不同差频叠加后碳钢球的TS-a曲线平滑效果

为进一步分析不同材料散射体的Δf选择问题，在与图4相同叠加条件下对铜球、铝球也分别进行了计算，发现铜球和铝球同样是在Δf=20 kHz时曲线平滑效果最好，150 kHz次之，500 kHz最差，与碳钢球的结果一致。Δf=20 kHz时三种材料的差频叠加效果的对比结果如图5所示，可见，三种材料此时的曲线平滑程度相近，铜的TS值略高于铝和碳钢。

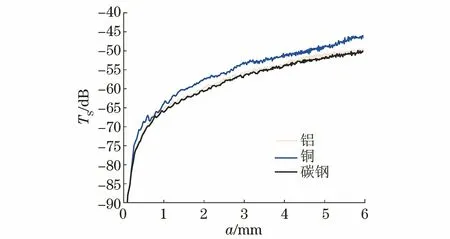
图5 Δf=20 kHz时三种材料弹性球差频叠加后的TS-a曲线

3 超声定量检测试验

利用图6所示的试验装置检验上述理论方法的有效性。先用螺旋测微器对7个弹性钢球的半径a进行测量，结果分别为5.0，5.5，6.0，7.0，7.5，9.0，10.0 mm，以此作为各球的实际半径。发射换能器中心频率为2 MHz，宽带水听器型号为PT-0800546，水听器接收点和待测钢球的几何中心位于换能器的声轴线上，且与发射换能器和钢球的间距分别为R1、R2。

图6 试验装置示意

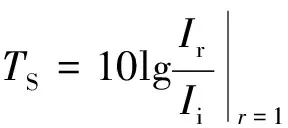
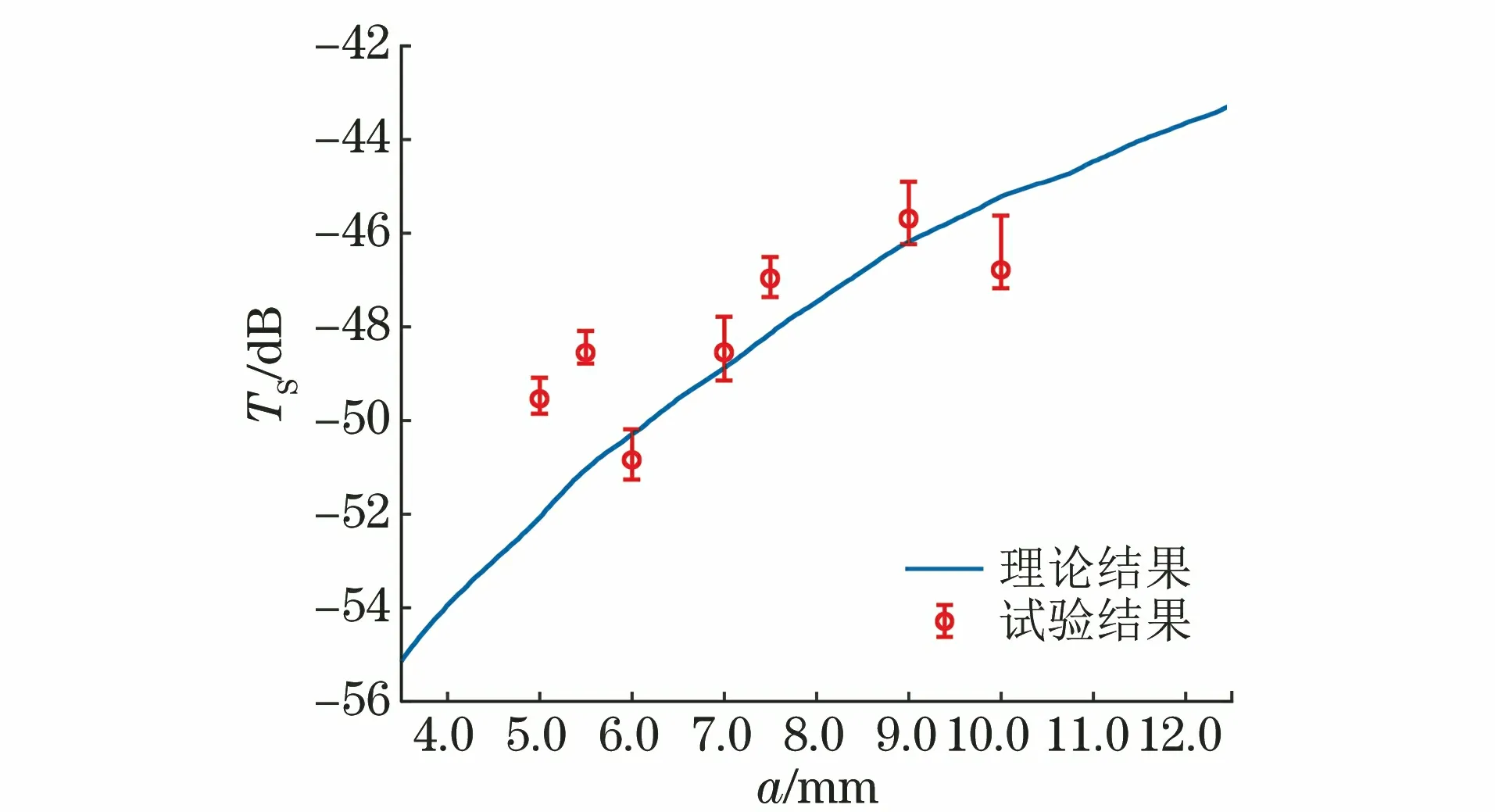
图7 不同球半径所对应目标强度实测值与理论化的对比结果

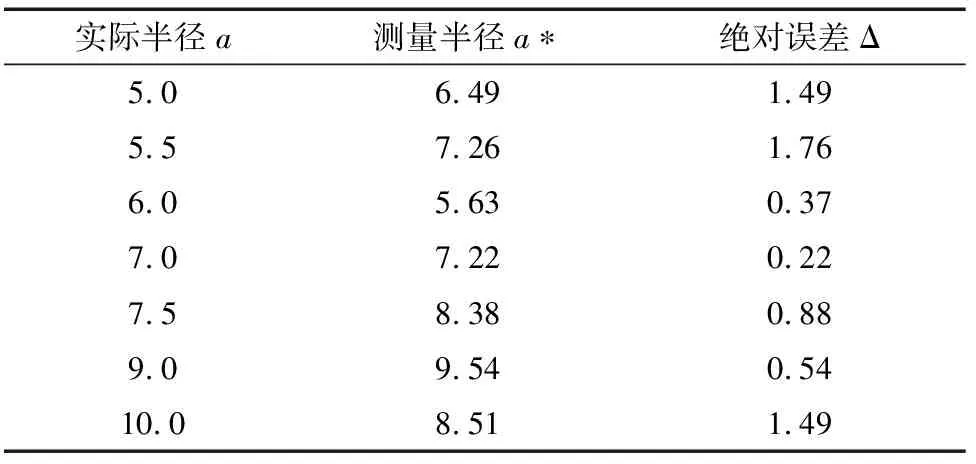
表1 钢球半径的超声定量结果 mm

4 结论

鉴于散射目标强度TS与散射球半径a存在多值性问题，提出了在一定频带内通过对TS差频叠加以减弱干涉，使TS～a满足单值对应的方法，并通过试验对该方法的有效性进行了验证，但该方法易受声信号接收角度的影响且仅对球形散射体有效。通过进一步研究发现，由多个阵元组成的相控阵探头可以接收多角度的散射波，是减弱、消除干涉的优选方法。另外，采用聚焦探头也便于对更多角度的散射波进行叠加、消除干涉，还能提高探头的分辨率，相对增大球半径的可检测范围和检测精度。