我国自然灾害风险预警模型*

张一洋 艾仁华 俞思雅 李 帆

(福州大学环境与安全工程学院，福建 福州 350108)

0 引言

自然灾害对社会发展造成严重影响，对自然灾害的特征、过程、损失以及其他后果等方面开展研究成为学界热点。例如张莹等[1]基于省际面板数据,对影响我国自然灾害损失的若干社会经济因素进行了检验和估计。He Yue等[2]以新浪微博的数据界定自然灾害的范围，并对灾区网络舆情进行研究。胡继亮等[3]建立Probit模型，研究自然灾害频率与损失度对于农户投保意愿的影响程度。

在进行自然灾害数据统计的过程中，研究人员嵌入时间因素对自然灾害情况进行分类说明。例如李媛媛[4]将新疆的自然灾害依照预警时间划分为三类。王萍等[5]对2000—2017年中国知识资源总库中关于灾害风险研究的中文文献进行分析，了解当前灾害风险研究领域现状和热点。景楠等[6]用时间序列数据,对新冠肺炎疫情构建舆情模型并进行参数估计、模型诊断和模型评价。Xu Xiaoyan等[7]应用经验模态分解和自回归综合移动平均相结合的预测方法研究自然灾害后的商品需求。毕硕本等[8]基于EEMD方法对1470—1911年黄河中下游地区旱涝灾害进行多时间尺度分析。Guo Naijing等[9]利用时间序列分析自然灾害和社会因素与灾情变化的相关性。张军[10]建立时间序列组合模型对四川省自然灾害直接经济损失进行趋势分析和预测。肖志权[11]利用时间序列预测模型获取受灾人群分布以及人口数量统计。

在对自然灾害的时间序列研究中，有部分关于自然灾害造成的经济损失和受灾人口的文献，但存在研究样本选取时间和空间跨度较小，以及分析变量较为单一的问题。本文系统梳理了2014年3月至2020年5月(共75个月)全国自然灾害造成的直接经济损失与受灾人口数据，以保证预警模型的全面和可靠。

1 时间序列定义

按照时间顺序排列所得的数组称为时间序列[12]。时间序列可分为平稳时间序列和非平稳时间序列两类[13]。非平稳时间序列数据不具备趋势，当数据存在趋势时,回归分析可能将无关变量拟合出显著的关联关系，这样的分析会得出错误的结论、做出无效的预测,即发生所谓的虚假回归,给实证研究和预测工作带来风险[14]。

1.1 变量定义

本文从国家灾情网和国家减灾网，收集了我国2014—2020年自然灾害导致的直接经济损失和受灾人口的数据，并绘制时间趋势图，见图1和图2。

图1 2014—2020年直接经济损失情况时间趋势图

图2 2014—2020年受灾人口情况时间趋势图

从图1和图2可以看出，受自然灾害影响的直接经济损失和受灾人口没有单调的时间趋势，且从现实而言自然灾害造成的直接经济损失和受灾人口根据每年受灾情况的不同而有所不同，一般不具有持续上升或下降的趋势，因此可以初步认为所选数据具有平稳时间序列的特征，但是需要进行实际的验证。

1.2 数据预处理

为减少由于数据方面出现的异常值和数据量纲方面的问题，将直接经济损失和受灾人口原始数据标准化，使数据保持在一个量级，能更好的进行分析预测，见公式(1)：

Zi=(Xi-μ)/δ

(1)

式(1)中，Zi为标准化后的值，Xi为原数值，μ为均值，δ为标准差。

1.3 单位根检验

由上文可知，直接经济损失和受灾人口没有明显的时间趋势，故采用无时间趋势的单位根检验，进而判断后面的序列是否平稳，结果见表1。

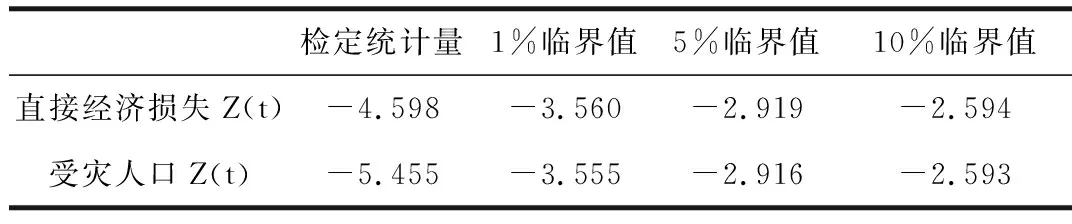
表1 直接经济损失和受灾人口单位根检验结果

从表1可见，直接经济损失和受灾人口的检定统计量分别为-4.598、-5.455，均小于各项检验值的临界值，即认为可以在1%的水平上拒绝“存在单位根”的原假设，所以认为直接经济损失和受灾人口是平稳的时间序列。

2 基于ARIMA的灾害风险预警模型

自回归积分滑动平均模型(Autoregressive Integrated Moving Average Model，ARIMA)是时间序列时域分析的方法之一[15]。ARIMA模型是在自回归滑动平均模型(Autoregressive Moving Average Model，ARMA)的基础上先对数据进行差分，再将差分还原得到预测数据，ARMA的一般表达式见式(2)。

(2)

式(2)中，yt为观测值，p、q分别为自回归阶数和滑动平均阶数，αi和βj分别为自回归系数和滑动平局系数，εt为白噪声。

2.1 相关性分析

通过观察自相关图与偏相关图，确定时间序列的ARIMA(p,d,q)模型的具体形式。其中，p值由自相关图的阶数确定，d是差分的阶数，q值由偏相关图的阶数确定。

2.1.1 自相关分析

首先绘制直接经济损失和受灾人口的自相关图，如图3和图4所示。

图3 直接经济损失自相关图

图4 受灾人口自相关图

从图3、图4看，直接经济损失和受灾人口的自相关图都具有二阶拖尾的特征。直接经济损失和受灾人口一阶自相关系数都超过了95%的置信区间，因此都存在一阶自相关。

2.1.2 偏相关

同理绘制直接经济损失和受灾人口的偏相关图，如图5和图6所示。

图5 直接经济损失偏相关图

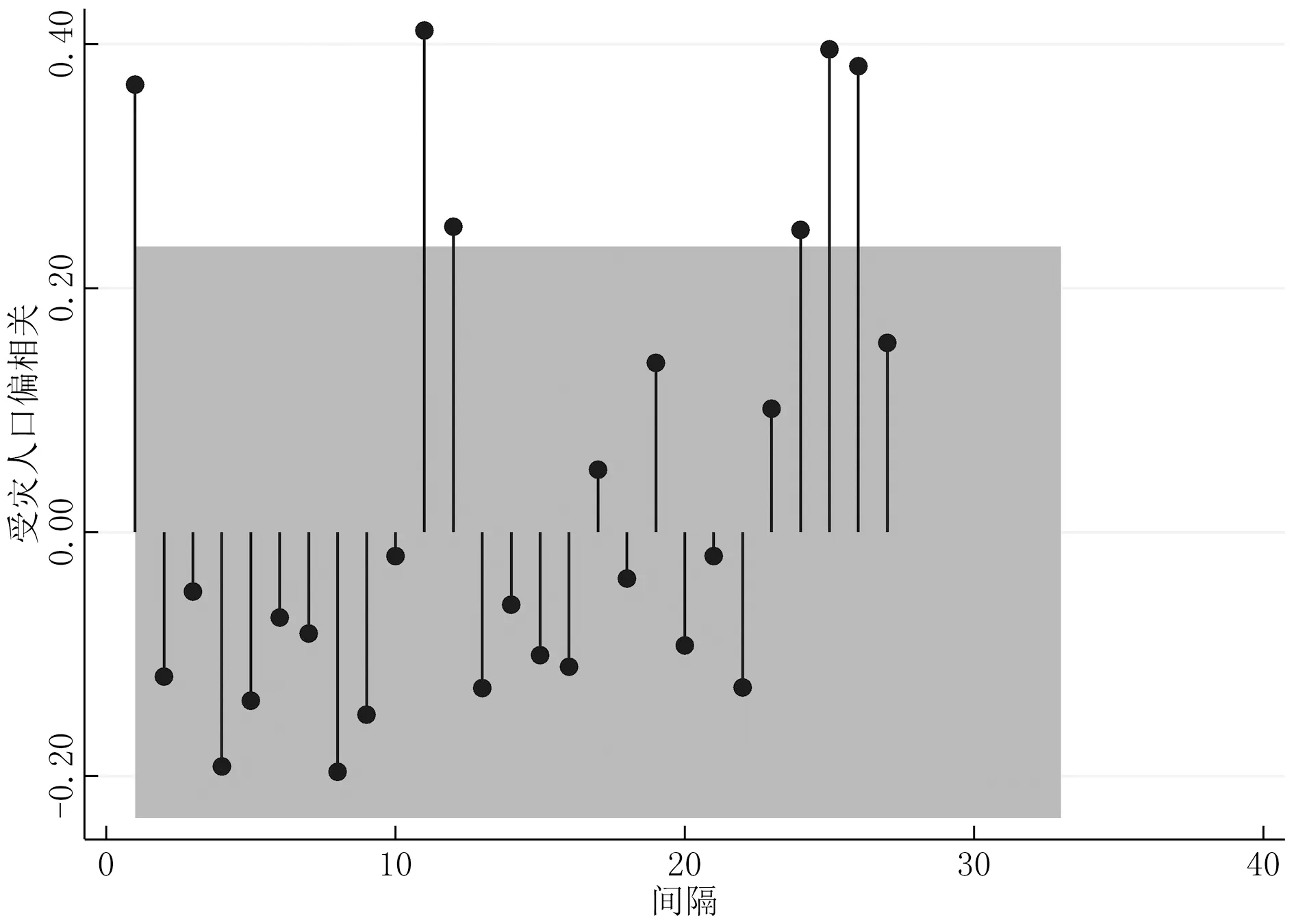
图6 受灾人口偏相关图

从图5、图6看，直接经济损失和受灾人口具有二阶截尾的特征。直接经济损失和受灾人口一阶偏相关系数超过了95%的置信区间，因此存在一阶偏相关。

综合自相关图和偏相关图来看，直接经济损失的自相关图具有二阶拖尾特征，而偏相关图具有二阶截尾特征；受灾人口的自相关图具有二阶拖尾特征，而偏相关图则具有二阶截尾特征，理论上两者均使用AR(2)模型，但还需要通过赤迟信息和贝叶斯信息进行判断。

赤迟信息准则(Akaike Information Criterion,AIC)和贝叶斯信息准则(Bayesian Information Criterion，BIC)是统计学中模型选择和评价的重要工具[16]。AIC和BIC可以权衡所估计模型的复杂度和此模型拟合数据的优良性，两者数值越小越好。

2.2 ARIMA模型

在Stata中，ARIMA模型被看作带有扰动项的结构模型,ARIMA模型公式中本质上使用的是最大似然估计。

直接经济损失原序列通过判断为平稳时间序列，因此ARIMA(p,d,q)模型中d=0，且自相关图具有二阶拖尾特征而偏相关图具二阶截尾的特征，理论上使用AR(2)模型。但是仍有其他4种模型进行选择，分别为ARIMA(1,0,1)，ARIMA(1,0,2)，ARIMA(2,0,1)，ARIMA(2,0,2),最终将通过对比AIC值和BIC值的大小来确定使用哪一个模型，结果见表2。

表2 直接经济损失AIC和BIC结果

对比AR(2)，ARIMA(1,0,1)，ARIMA(1,0,2)，ARIMA(2,0,1)，ARIMA(2,0,2)的AIC值和BIC值，ARIMA(2,0,2)的AIC值和BIC值最小，因此选择ARIMA(2,0,2)模型。

同理，受灾人口的检验结果如表3所示。

表3 受灾人口AIC和BIC结果

对比AR(2)，ARIMA(1,0,1)，ARIMA(1,0,2)，ARIMA(2,0,1)，ARIMA(2,0,2)的AIC值和BIC值，ARIMA(2,0,2)的AIC值和BIC值最小，因此选择ARIMA(2,0,2)模型。

3 白噪声检验

拟合模型后，需要检验残差序列是否为白噪声。生成新的残差序列，直接经济损失残差序列r1和受灾人口残差序列r2，在正常情况下生成的残差应为平稳时间序列。绘制残差图，见图7和图8。

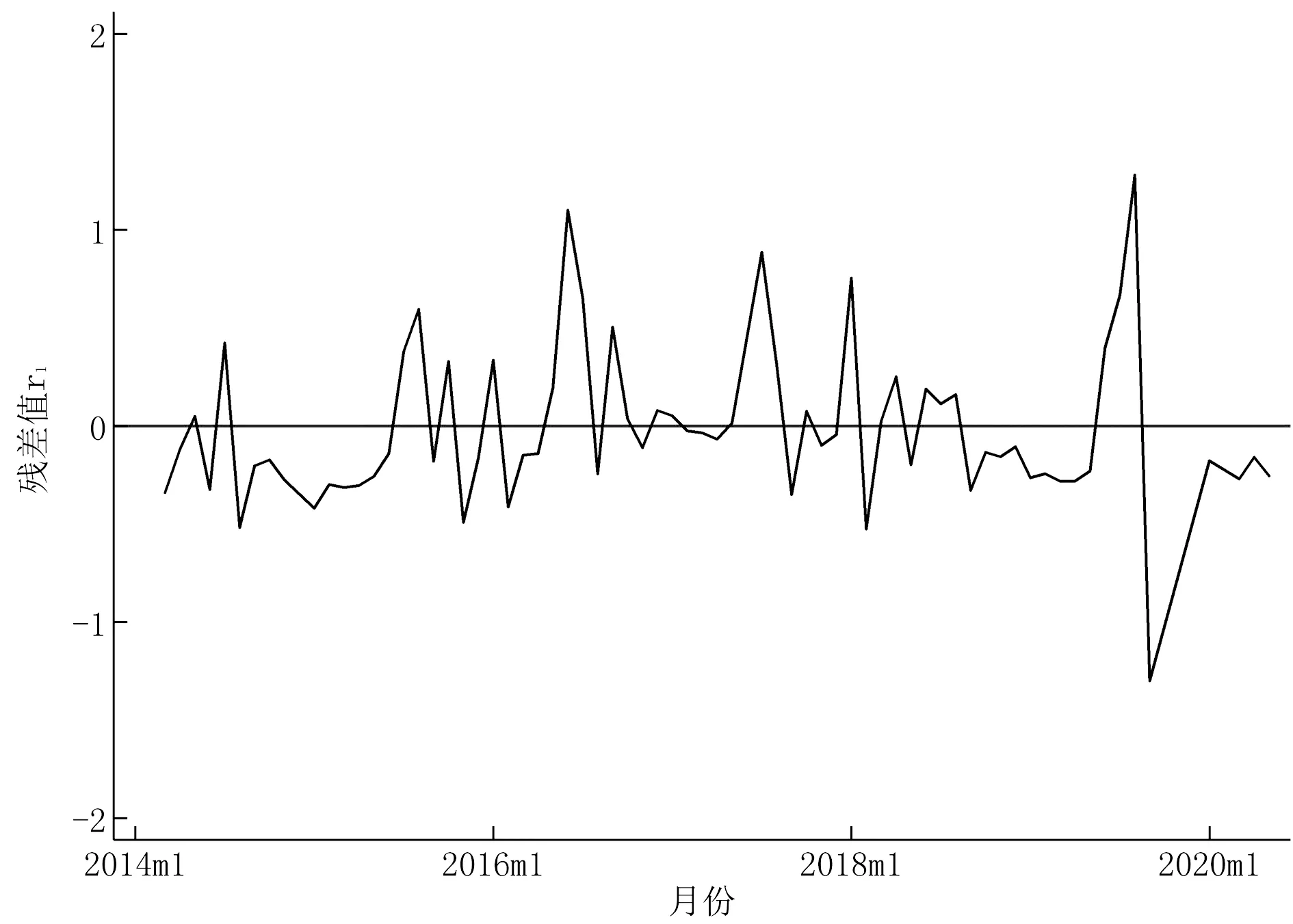
图7 直接经济损失残差图

图8 受灾人口残差图

从图中可以直观看出，直接经济损失和受灾人口的残差序列无明显的上升或者下降趋势，可认为是平稳时间序列。为确定最终结果，还需对残差进行单位根检验，结果见表4。

表4 残差单位根检验结果

根据表4结果可知，直接经济损失和受灾人口的检定统计量分别为-7.471和-6.574，均小于各项检验值的临界值，即认为可以在1%的水平上拒绝“存在单位根”的原假设，所以认为直接经济损失和受灾人口的残差值是平稳的时间序列。

系数显著性检验通过后，要进行模型的有效性检验，也就是检验残差性是否为白噪声，用Q统计量进行白噪声检验，检验结果见表5。

表5 白噪声检验结果

从检验结果来看，r1的P值为0.3321>0.05，可以认为存在白噪声，因此该序列的信息已经被提取完毕，可知模型的拟合性较好。而r2的P值为0.0014<0.05，认为不存在白噪声，因此模型不合理，故重新对ARIMA模型进行选取。按照AIC值和BIC值从小到大进行选取，选出白噪声检验合格的ARIMA模型，结果见表6。

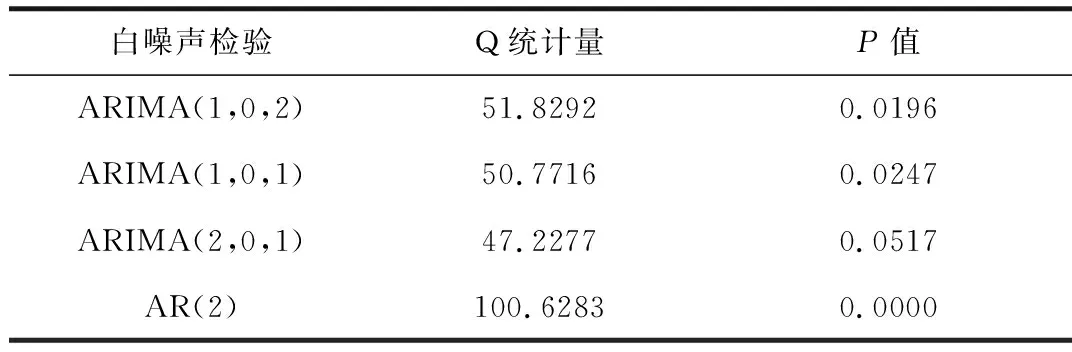
表6 受灾人口残差值检验

根据表6的结果，只有ARIMA(2,0,1)模型的P值满足要求为0.0517>0.05，可以认为存在白噪声，因此该序列的信息已经被提取完毕，可知模型的拟合性较好，可以开始模型的预测。同时，从其残差图(见图9)和单位根检验(见表7)来看，ARIMA(2,0,1)模型也满足条件。

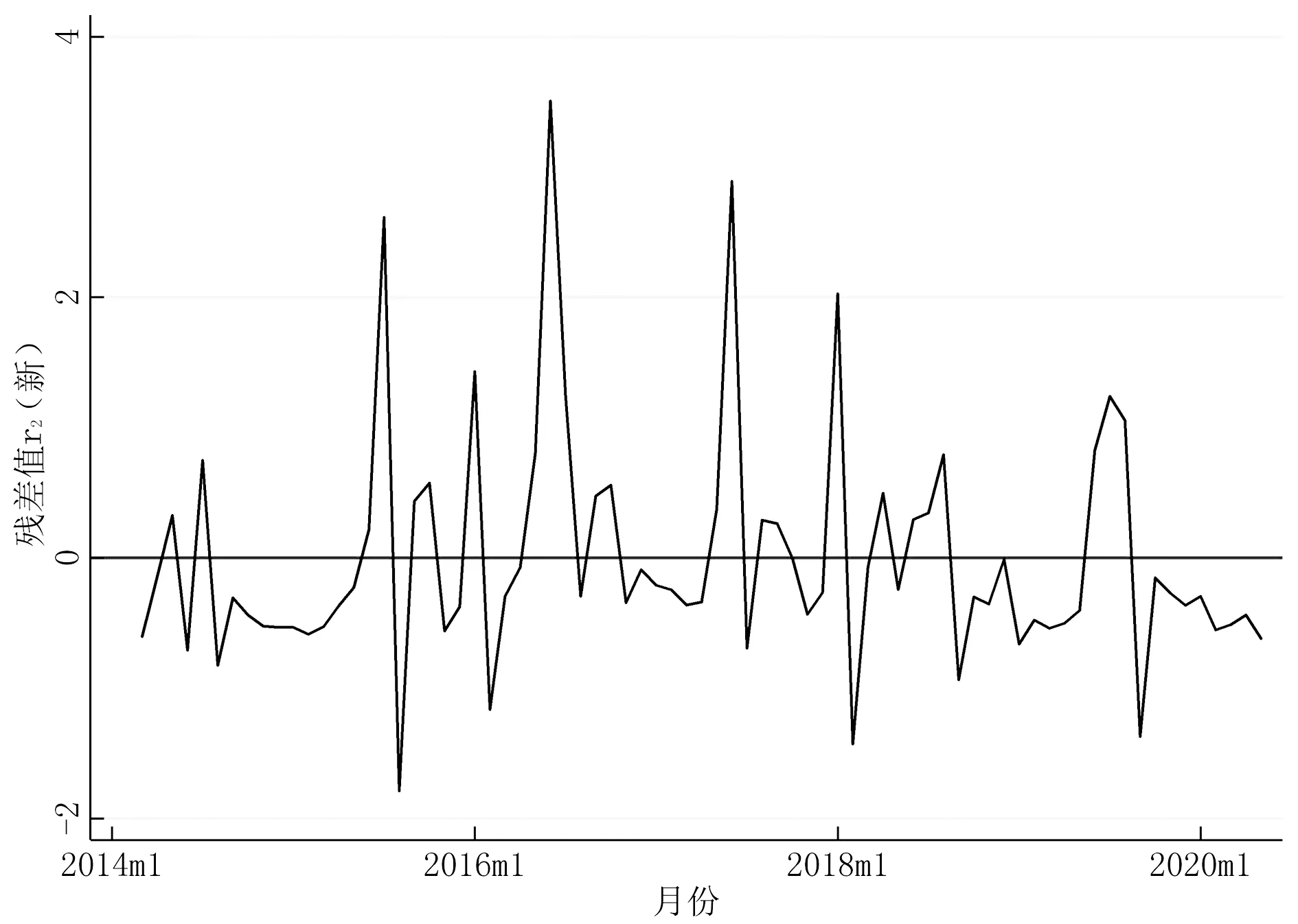
图9 受灾人口残差图(新)

从图9可以看出,受灾人口的残差序列无明显的上升或者下降趋势，可认为受灾人口是平稳时间序列。

表7 残差单位根检验结果(新)

根据结果检定统计量的值为-7.681，均小于各项检验值的临界值，即认为可以在1%的水平上拒绝“存在单位根”的原假设，所以认为残差值是平稳的序列。

综上结果来看，最终选定直接经济损失的ARIMA模型为ARIMA(2,0,2)，受灾人口的ARIMA模型为ARIMA(2,0,1)。

4 风险预警效果分析

4.1 样本内预测

对于模型，研究先采用样本内数据进行估计[17]。样本内预测是使用预测模型对样本内的原始值进行预测，其与实际样本的差异即为残差值。生成新的直接经济损失和受灾人口的时间序列作为预测值，将其比对原始值的拟合线，见图10和图11。

图10 直接经济损失样本内预测

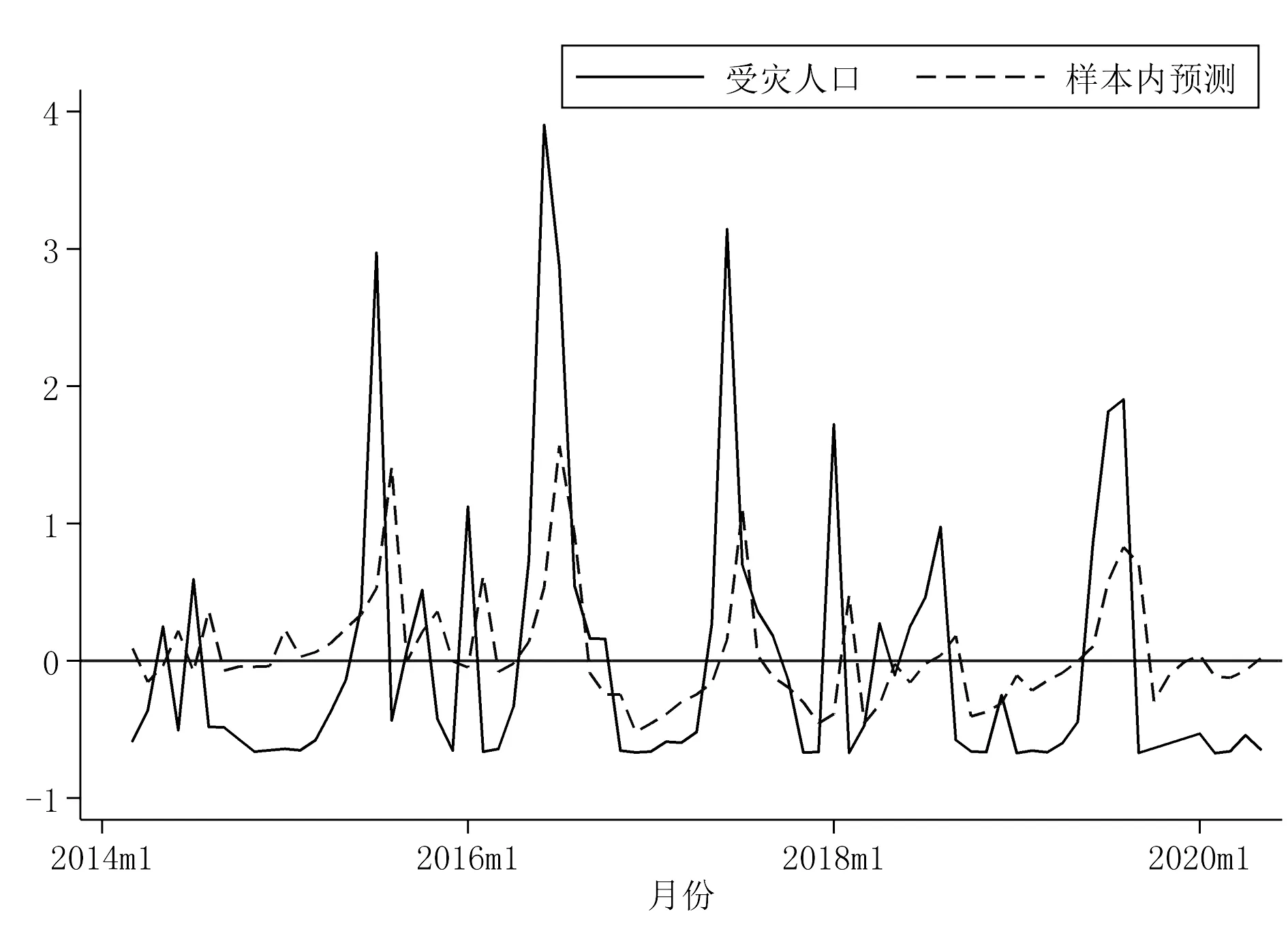
图11 受灾人口样本内预测

图10、图11中，实线为原始值，虚线为样本内预测值。ARIMA模型对实际值进行了更为平均的计算，从直观轮廓可以看出，图中预测值与原始值时间趋势相同，因此可以认为所选预测模型有一定的拟合效果。相比于直接经济损失的模型，受灾人口的模型整体拟合效果稍弱，但能其在时间节点的上升或下降趋势与原始数据相近，能从直观轮廓中看出受灾人口的历年变化趋势，因此认为所选预测模型有一定的拟合效果。从拟合的结果来看，在同一年内一般具有两个较大的起伏，最高值分别处于夏季7月份和冬季1月份，最低值分别处于春季3月份和秋季11月份，最高值约为最低值的2～4倍。

4.2 样本外预测

样本外预测效果在未来预测方面更具有说服力[18]。样本外预测首先要填补空缺值，Stata软件能对未来一定时间内的情况进行预测，该范围取决于时间序列的单位，本文以月份为单位，新添加了12个月的空缺值，即时间范围达到2021年5月末。生成新的时间序列作为样本外预测值，将其与原始值进行比对，结果见图12和图13。

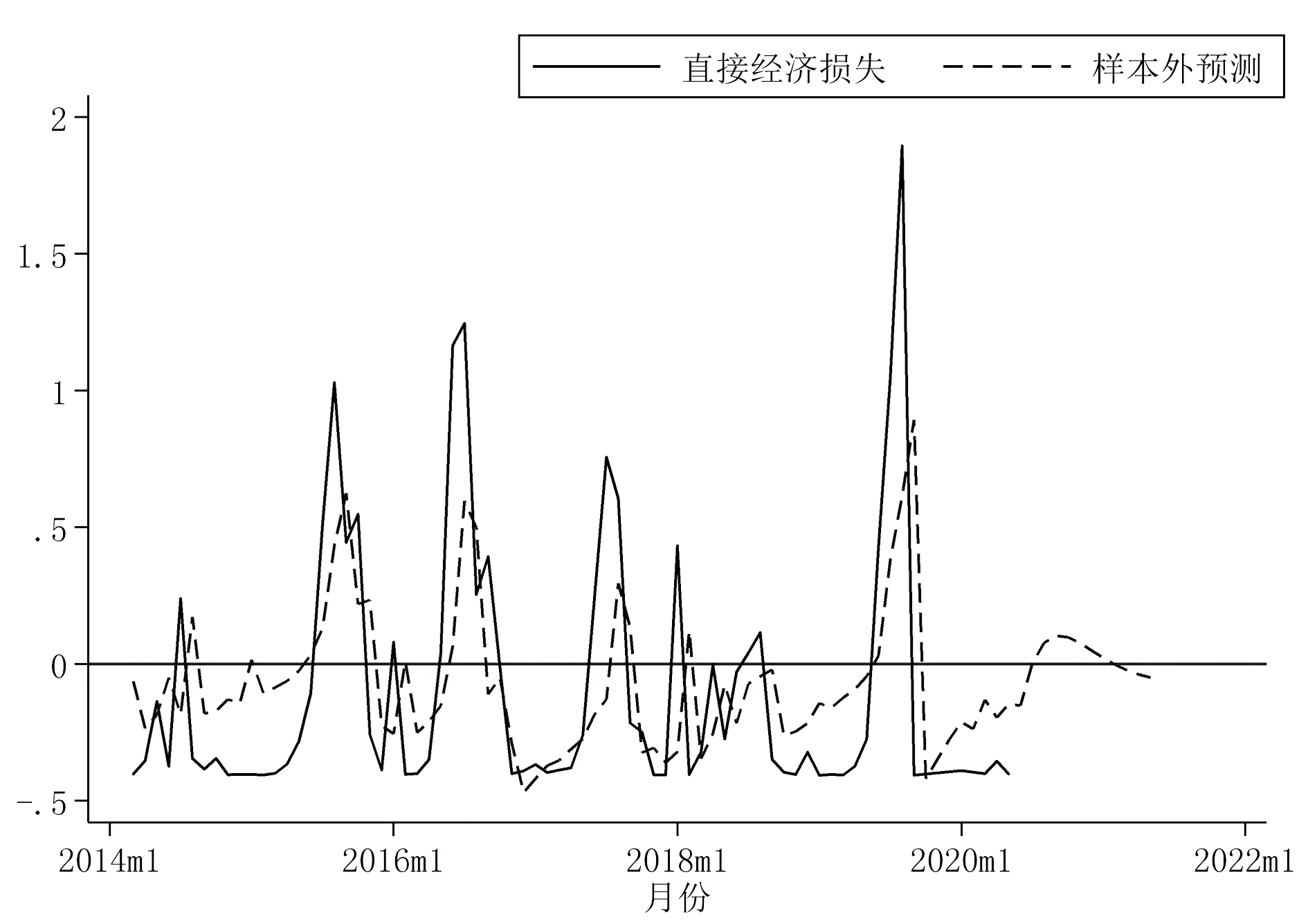
图12 直接经济损失样本外预测

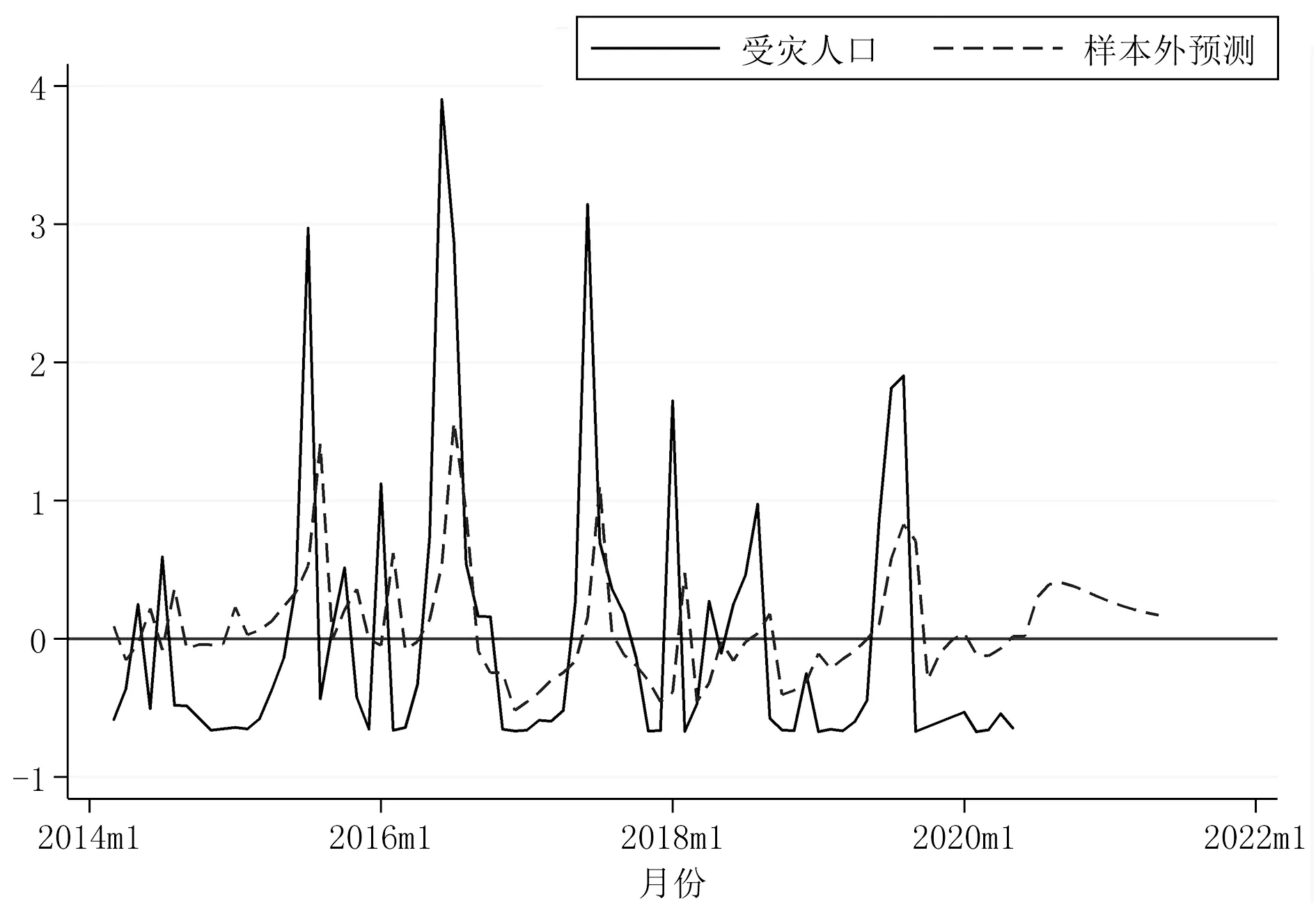
图13 受灾人口样本外预测

图12和图13中实线为原始值，虚线为样本外预测值。样本外预测是在样本内预测的基础上进行的，从图12和图13可以看出，样本外预测值相较于原始值多出了一部分，该部分即为2020年6月初至2021年5月末的直接经济损失和受灾人口的预测值。从预测值的结果来看，接下来的12个月直接经济损失和受灾人口整体呈先上升再下降的趋势。预测时间从2020年6月开始，此时处于夏季，是自然灾害的频发阶段，图中的预测结果显示在接下来的时间中，自然灾害导致的直接经济损失和受灾人口将会上升，这与实际情况相符合，但是在整体预测中只出现了一个较大的起伏，另一起伏表现不明显。

5 结论

①对比直接经济损失和受灾人口时间趋势图发现，两者变化趋势基本相同，即自然灾害造成经济损失的同时也会产生受灾人口。一般来讲，直接经济损失高，受灾人口也多，但是并非绝对，而是与具体造成损失的自然灾害有关。

②由相关性分析得到直接经济损失和受灾人口的自相关和偏相关系数，并由AIC值和BIC值得到时间序列模型。通过白噪声检验和残差值检验，最终选定两者的时间序列模型。

③从样本内预测来看，新生成的模型与原始值有一定差值，但是具有相同的起伏趋势，预测值也满足在冬夏季节直接经济损失和受灾人口多的特征。从样本外预测来看，生成的模型是在样本内预测的基础上形成的，具有样本内预测的特征。得到的结果满足从春季到夏季先升后降的趋势，与实际情况比较符合，对于预测未来直接经济损失和受灾人口有一定参考意义。