基于最小二乘法的桥梁结构刚度损伤识别研究

耿 栋，崔后吉，王 乐

（1.安徽省公路工程检测中心，安徽 合肥 230051；2.桥梁与隧道工程检测安徽省重点实验室，安徽 合肥 230051）

桥梁作为公路工程中的重要节点工程，对社会的经济发展及人民的日常生活起到了非常重要的纽带、衔接作用。建国70 多年来，随着我国经济的大发展，基建工程中尤其是桥梁工程发展相当迅速，如今已成为世界的桥梁大国。然而，近几十年来国内外桥梁事故多有发生，如2012年8月江西广昌河东大桥垮塌，2012年5月湖南平江大桥垮塌等。国外的桥梁事故也不乏鲜见，美国明尼苏达州的35 号洲际公路上一座建成40年的钢筋混凝土大桥在2007年8月突然发生坍塌。在桥梁事故中，独柱墩桥、曲线桥等类型桥梁倒塌受到了特别关注。2019年10月10日18 时10 分许，江苏省无锡市312 国道K135 处锡港路上跨桥发生侧翻事故，侧翻桥梁为独柱墩桥梁结构。资料显示，国内最早的独柱墩桥、曲线桥倒塌事故发生在2007年10月23日，包头市民族东路高架桥突然发生倾覆，事故由三辆半挂牵引重型货车由南向北行驶至桥面造成。此后，类似事故时有发生。

近年来，重大工程结构的安全服役问题越来越突出，对于这些结构的状态监测，损伤状态评估，以及损伤后的安全性评价的理论研究已成为工程结构安全性研究的重要理论需求，并有着广泛应用前景[1]。自90年代开始，一些重大的工程结构安装了结构健康监测系统并获得了大量的数据，然而，基于目前结构健康监测的理论还很难有效地从采集的海量数据中提取出结构的特征参数并对结构的损伤进行识别，更难针对结构的实时状态来进行结构安全评估，从而给结构安全研究带来巨大的挑战[2]。

在桥梁健康监测中结构位移是桥梁监测的关键参数之一。随着国内桥梁尤其是独柱墩桥、曲线桥等类型桥梁需求的增加，桥梁服役过程中结构位移特征引起广泛关注，例如主梁挠度、桥墩沉降位移、支座位移等。桥梁结构位移作为变形的一种描述形式，是桥梁构件受力最明显的反应，反映桥梁构件的工作状态，可以用于评价桥梁刚度及安全性能[3]。

综合国内外研究现状分析发现，大型复杂结构工作刚度损伤识别，尽管有许多的处理方法和研究成果，但还远不能够说是一个已经完全解决了的课题[4]。特别是长期运营中的土木工程结构，由于环境的变化，荷载的变化，以及损伤的积累导致刚度的退化，均会导致结构特性参数随时间变化。同时大部分土木工程结构在一定程度上表现出非线性行为，如材料本身的非线性导致结构的非线性，结构边界条件及状态的非线性，结构在长期荷载或突发荷载作用下发生损伤，也会表现出非线性行为[5]。因此，长期荷载作用下的这些结构，本质上属于时变和非线性结构系统。这就需要能识别结构的时变和非线性参数的理论和方法[6]。本文正是考虑到桥梁结构在极端荷载作用下，由于损伤的积累导致结构表现出双线性的行为，研究基于最小二乘法的桥梁结构刚度损伤识别方法，对结构在极端荷载下的安全评估具有较大的理论与工程应用价值。

1 研究方法

对具有双线性刚度的桥梁结构，在较小荷载作用下桥梁结构保持结构原有的刚度，然而随着荷载的增加，结构的损伤发生，导致桥梁结构的刚度降低。本文正是针对桥梁结构的双线性行为，利用最小二乘法对双线性刚度进行识别。在外荷载作用下的线性桥梁结构，通过一系列的荷载试验，可以利用经典的最小二乘法来估计桥梁结构的线性刚度的解析闭合解[7]。然而对于双线性桥梁结构，国内外的文献中还很难找到基于最小二乘法的双线性刚度识别的闭合解，因此，本文将通过系列理论研究推导桥梁结构双线性刚度的最小二乘法识别方法。

双线性刚度的桥梁结构的位移-荷载曲线如图1所示，其中Δ 为位移，P为外荷载。

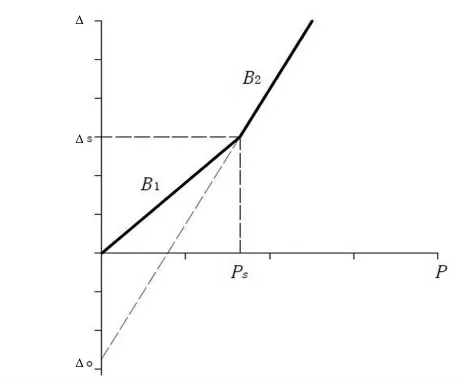
图1 双线性刚度桥梁结构的位移-荷载关系

双线性刚度桥梁结构的位移可表示为：

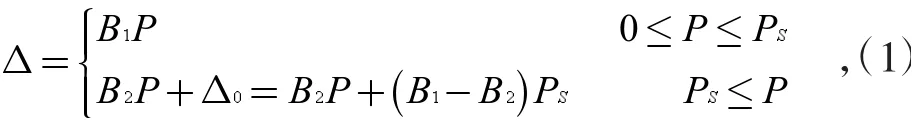
上式中Ps表示过渡荷载，其值即为图1 中两条直线交点的横坐标值。Δs 表示过渡荷载作用下的结构位移，其值即为图中两条直线交点的纵坐标值。B1和B2分别表示两条直线的斜率。Δ0表示斜率为B2的直线在y轴上的截距。

假设有一系列的荷载作用在桥梁结构上，并产生一系列的位移响应，这时荷载、位移可表示为Pi、Δi（i=1~n）。对于过渡荷载Ps是假定为已知的，这是因为桥梁结构在外荷载作用下其刚度发生明显变化的时候往往伴随着明显的破坏特征，比如混凝土结构在其所受荷载达到过渡荷载时会出现较大的裂纹和较大的塑性变形等，而这时过渡荷载就可以被合理地监测得到。虽然过渡荷载是已知的，但过渡位移却不是已知的，这是因为结构的刚度是未知的。对于荷载小于或等于过渡荷载时，荷载、位移分别表示为P1i、Δ1i（i=1~n1），对于荷载大于过渡荷载时，荷载、位移分别表示为P2i、Δ2i（i=1~n2），其中n1+n2=n。为了识别出双线性桥梁结构在承受大于过渡荷载Ps后的刚度损伤，本文将推导基于最小二乘法的双线性最小二乘法。该方法的基本思路是对求双线性结构的位移残余误差平方和最小值，即：

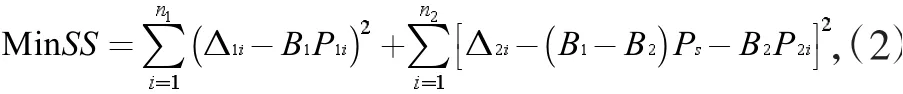
上式是一个标准的线性最小二乘法方程。由于过渡荷载Ps是已知的，所以公式（2）中有两个未知量B1和B2。为使公式（2）达到最优解即结构的位移残余误差平方和取最小值，公式（2）对B1、B2两个未知量的偏导数函数等于0，因此可以解析出B1和B2。综上所述，双线性最小二乘法在理论上能够很好地识别出双线性结构的刚度。因此本文的主要内容就是要推导出基于双线性最小二乘法的双线性刚度识别的理论解。

2 研究内容

推导具有双线性刚度的桥梁结构刚度的双线性最小二乘法的理论解。

公式（2）是一个标准的线性最小二乘法方程。由于过渡荷载Ps是已知的，所以公式（2）中有两个未知量B1和B2。为使公式（2）达到最优解即结构的位移残余误差平方和取最小值，故公式（2）必须满足其对B1、B2两个未知量的偏导数函数等于0 这一条件。

公式（2）对B1的偏导数方程为

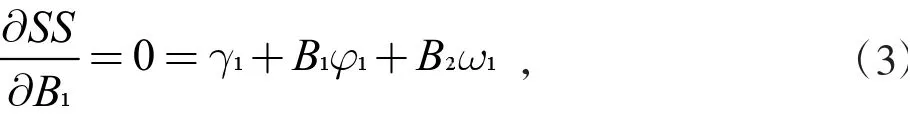
其中：

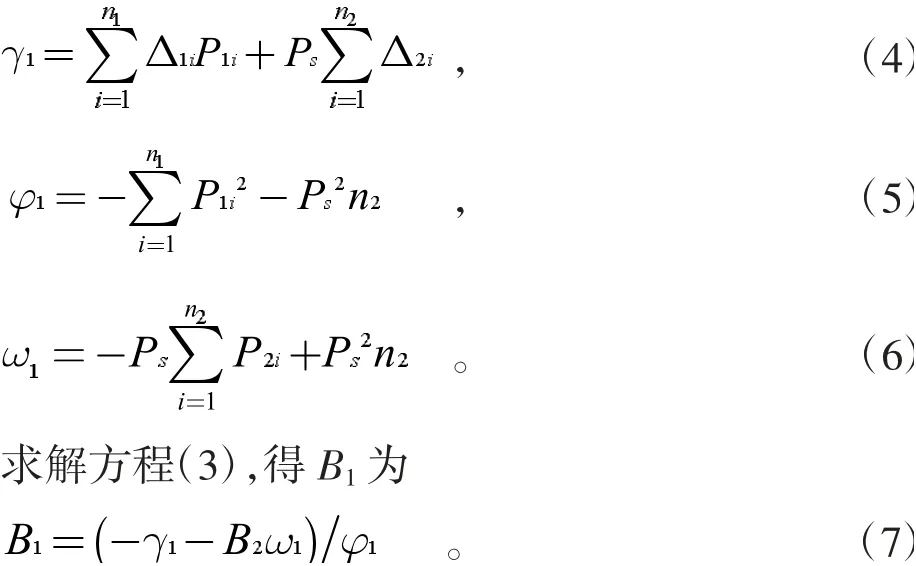
方程（2）对B2的偏导数方程为

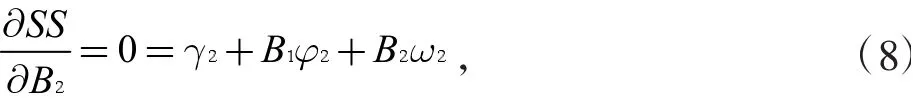
其中：

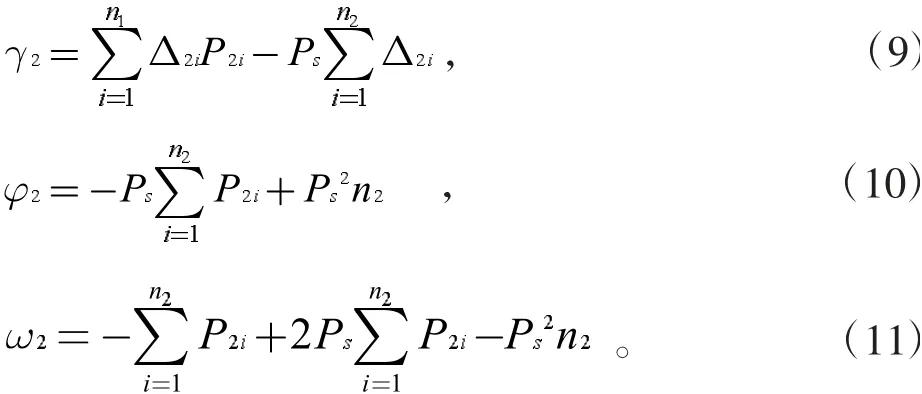
然后，将方程（7）代入到公式（8）中，解得B2为

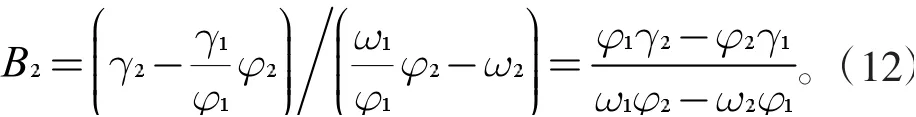
再将B2的结果代回到公式（7）中，得B1为

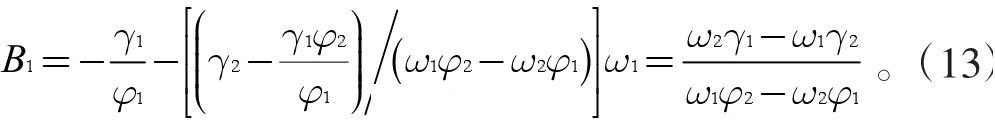
3 数值模拟

为了验证基于最小二乘法识别桥梁结构的双线性刚度的有效性。本文对混凝土简支梁在竖向集中荷载作用下的位移响应进行数值模拟。数值模拟中的混凝土简支梁全长为6 m，其梁横截面为矩形，梁高为0.2 m，梁宽为1.2 m，梁横截面面积为0.24 m2，梁的截面惯性矩为8×10-4m4，弹性模量为32.5 kN/mm2，容重为25 kN/m3。数值模拟的简支梁纵向布置图如图2 所示。

图2 数值模拟混凝土简支梁纵向布置图

数值模拟中简支梁的竖向集中力作用在梁跨中顶部位置，集中荷载逐级加大，记录每级荷载P1i，利用有限元计算软件计算出每级荷载作用下的梁跨中位移Δ1i。桥梁结构在外荷载作用下其刚度发生明显变化的时候往往伴随着明显的破坏特征，比如混凝土结构在其所受荷载达到过渡荷载时会出现较大的裂纹和较大的塑性变形等，而这时过渡荷载就可以被合理地监测得到。本次数值模拟对过渡荷载进行合理假设，并利用降低截面惯性矩的方法来模拟简支梁损伤，随着损伤程度增加，截面惯性矩也相应进行调整。简支梁发生损伤后，继续分级增大荷载，并记录为P2i，利用有限元计算软件计算出简支梁损伤后每级荷载作用下的梁跨中位移Δ2i。

对计算得到的数据进行整理，利用图表工具绘出P、Δ 数据分布图，如图3 所示。根据P、Δ 数据分布特点，本次数值模拟假设过渡荷载Ps为45 kN。利用双线性最小二乘法分别识别出简支梁在过渡荷载前后的构件刚度B1、B2。利用本文研究内容推导的公式，计算得到B1为0.174 mm/kN，计算得到B2为0.497 mm/kN。根据计算得到的简支梁过渡荷载前后的构件刚度，绘出P-Δ 线形关系，结果如图4 所示。

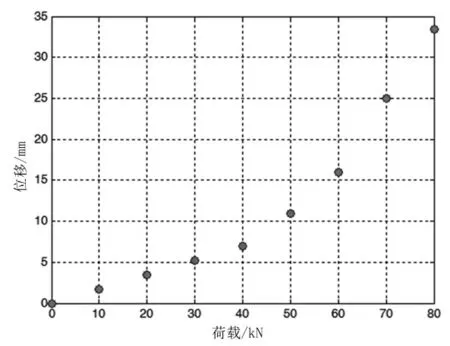
图3 简支梁加载过程中P、Δ 数据分布图

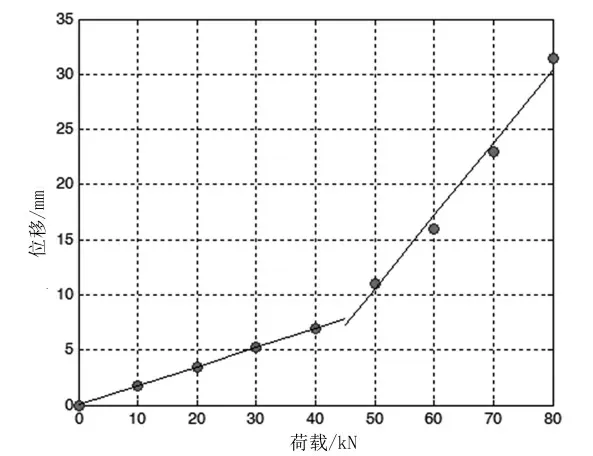
图4 计算得到简支梁P-Δ 线形关系图

根据图4 所示结果，可以看出利用双线性最小二乘法能够分别识别出简支梁损伤前后的构件刚度，计算得到的荷载、位移线形关系与实际荷载、位移数据分布有较高的吻合度。

根据图4 所示结果，还可以看出荷载、位移线形关系在梁结构损伤前后发生明显变化。损伤后的简支梁在荷载作用下发生的位移更为明显。对于梁结构损伤程度的定量分析，本文给出如下公式进行计算。

上式中D表示梁结构刚度损伤程度，B1和B2分别为梁结构损伤前后的刚度。根据公式（14）计算得到，本文数值模拟中简支梁的刚度损伤程度为65%，损伤较为明显。

4 结论

综上所述，基于最小二乘法能够很好地识别出桥梁结构的双线性刚度，利用识别出来的双线性刚度可用于对桥梁结构的损伤进行有效识别。