基于贝叶斯压缩感知与SVM 算法的智能化勘察研究

张 锐

（华设设计集团股份有限公司，江苏 南京 210014）

在当前工程勘察中，对于土层划分和土的参数确定传统上主要依赖于CPT、SPT 等原位测试及取样试验，基于标贯击数和锥尖阻力、侧阻力等物理指标划分地层一直是国内地质勘察工作者最常用的方法，也是最主要的经验方法之一[1]。但是由于土的离散性以及收集的数据有限，很难对场地的分布有细致准确的描述。且钻孔与钻孔之间的距离间隔很大，尤其在公路、隧道等线性工程中，考虑到成本等因素，钻孔的间隔甚至达到了100 m 以上，数据存在很大的不确定性。对于钻孔之间的地层情况难以准确预测，钻孔之间出现土的断层、错动影响[2]，相邻每个钻孔测得的土层种类不一致等问题。因此，基于稀疏地层数据的插值扩充工作显得格外重要。

香港城市大学WAND 等[3-5]基于美国某地静力触探实验数据（锥尖阻力，侧阻力）提出了一种基于贝叶斯压缩感知（Bayesian Compressive Sampling，BCS）的钻孔数据插值扩充方法。BCS 是传统压缩采样（Compressive Sampling，CS）方法的概率扩展，其本质是从信号的部分信息中重构出一个信号的完整信息[6-7]。在岩土工程中，土层性质随深度而变化，因此土层性质剖面可被视为信号进行分析。BCS 方法不仅能从有限的测量数据中合理地解释土层性质剖面，而且还提供了量化与解释剖面相关的统计不确定性的实用工具，量化的统计不确定性为分析的土性质剖面的准确性和可靠性提供了一个衡量标准[8-9]。

在得到充分的勘察数据之后，对于地层的划分一直是研究的热点问题，划分结果的准确性关系到后期工程的安全性和可靠性。我国对土层划分暂无统一的标准，实际工程勘察中多采用SPT 标贯实验和取土钻孔相结合的勘察方法，根据现场取出的实际土样通过经验判断，确定土层的划分。刘松玉等[10]对我国SPT 技术做出了全面的分析，目前采用的《岩土工程勘察规范》《水利水电工程地质勘察规范》和《公路工程地质勘察规范》中采用的分类标准都不尽相同。随着科技的不断进步，关于地层的划分工作已经不仅仅局限于传统的SPT 法、取土分析法等，近年来人工智能技术在工程勘察领域发展得十分迅速，SVM、聚类、神经网络等在国内外地层划分上也取得许多研究进展[11-13]。

本文基于苏州某地块的工程勘察数据进行实例计算分析，采用贝叶斯压缩感知方法对贯入阻力数据进行二维插值扩充，得到整个勘察剖面的贯入阻力分布情况。随后利用支持向量机（SVM）算法对扩充数据进行分类，得到整个地层剖面的划分，从而实现基于少量钻孔信息，即可得到较为准确的地层分布情况，为工程勘察提供智能化技术支持。

1 二维贝叶斯压缩感知原理

1.1 插值矩阵计算

贝叶斯压缩感知是一种信号处理技术，其最大优势是可将收集的稀疏信号进行插值扩展，实现原始数据的重构，广泛应用于各个领域。工程勘察可以认为是对地层数据的稀疏取样，贝叶斯压缩感知可根据稀疏数据有效地重构地层数据。例如地层剖面上的钻孔测得的比贯入阻力可以用插值矩阵F来表示，F可以视为一个二维矩阵，维度大小为（Nx1×Nx2，可根据实际场地自行取值）。Nx1为深度方向长度，Nx2为水平方向长度，由于地层的信息为离散数据，需要用到插值辅助函数等一系列方法，插值矩阵F的计算公式如下：

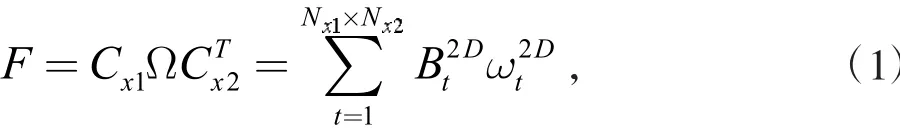
式（1）为贝叶斯压缩感知的基本公式，式中各类参数的计算和构造方法在下述小节将做出详细介绍和推导。

1.2 离散余弦矩阵（DCT）构造

式（1）中，Cx1（Nx1×Nx1）和Cx2（Nx2×Nx2）为离散余弦矩阵，AHMED 等[14]基于傅里叶变换法提出了离散余弦变化（DCT）公式，本研究对DCT 公式进行了展开，化简为矩阵的形式，其数学公式较为复杂，但可利用Python代码构建Cx1和Cx2矩阵，具体见表1。

表1 离散余弦矩阵构造

式（2）中，i表示Cx1的列，j表示Cx2的行，为了方便推导避免引起混淆，将二维索引i，j转化为一维索引t。下标t是通过以升序对B2D列中的所有元素进行编号来定义的，即将二维矩阵按列展开，变为索引从1~Nx1×Nx2的一维数组。在同一列中，t随着行数的增加而增加，例如则可以表示为

1.3 超参数定义及迭代

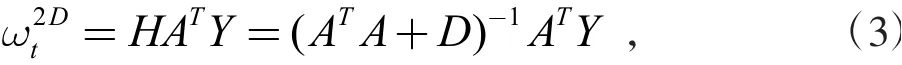
式中，Y为原始数据集（插值矩阵F的子矩阵），维度为与插值矩阵F的关系如式（4）所示：

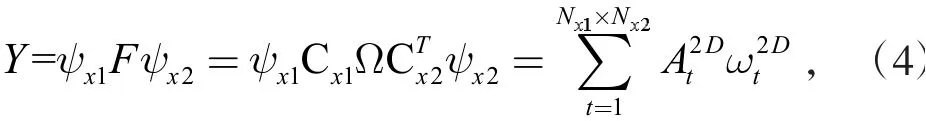
A=为定位矩阵，反映了数据集Y作为插值矩阵F的子矩阵在F中的行列索引，可由单位矩阵轻松构造。D是维度为（Nx1×Nx2，Nx1×Nx2）的对角矩阵，其对角线的值为αi，如式（5）所示：

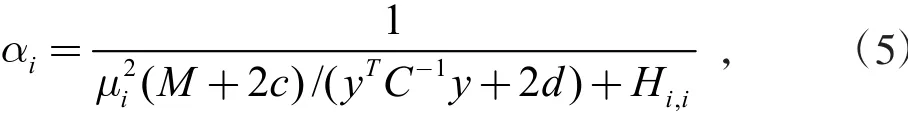
式中，M=Nx1×Nx2，c，d为超参数取值，可以使用HUANG等[15]人提出的策略迭代法获得c和d，一般取值为0.000 1，C＝IM×M+AD-1AT，I是单位矩阵，其维度为（Nx1×Nx2，Nx1×Nx2）。

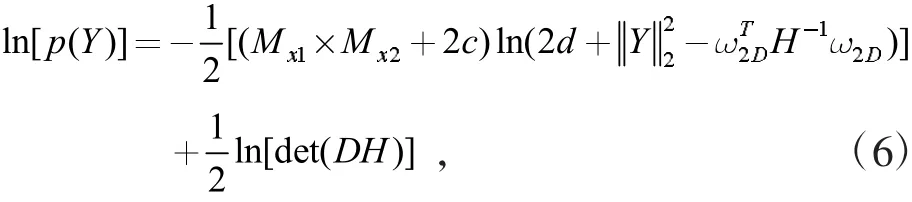
2 研究场地概况

本文选用苏州蕾娜斯地块场地静力触探实验数据进行贝叶斯插值。场地拟建主体建筑为地上三层，地下一层，框架结构的多层古建及宾馆。

如图1 所示，选取该区域第2 剖面为研究场地，该场地剖面长度为113 m，静力触探孔编号7~12，共计6个，钻孔水平间隔分别为23 m，22 m，25 m，23 m，20 m。该剖面在水平方向较为平整且钻孔位于同一轴线上，计算误差相对较小。

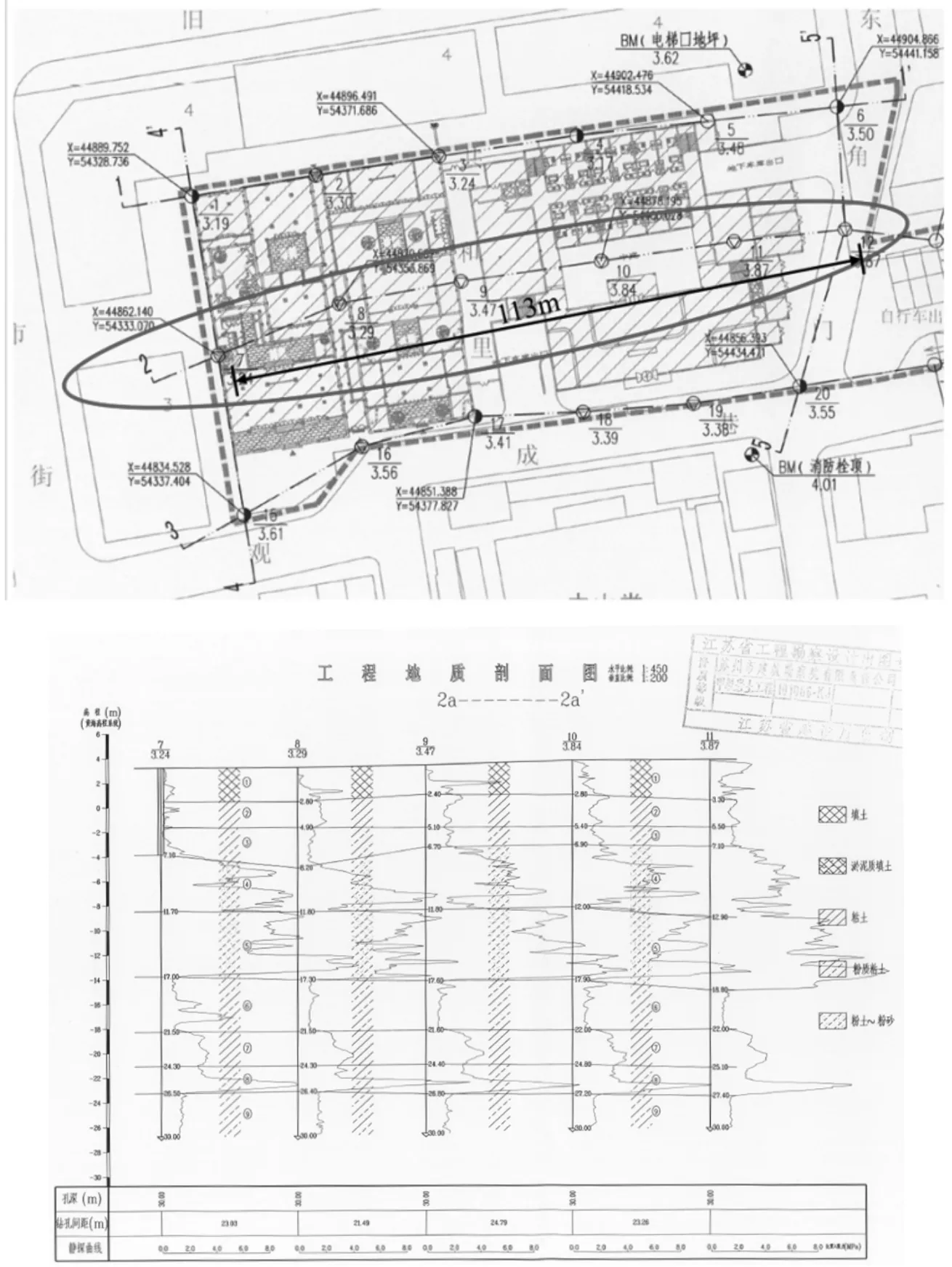
图1 研究剖面示意图

如图2 所示，将钻孔深度和对应的比贯入阻力画成二维图像，每组钻孔深度为30 m，钻孔的比贯入阻力沿深度方向间隔0.5 m，比贯入阻力由于土层不同，大致分布在0~15 MPa 之内（以7 号钻孔为例，8~12 钻孔同理）。

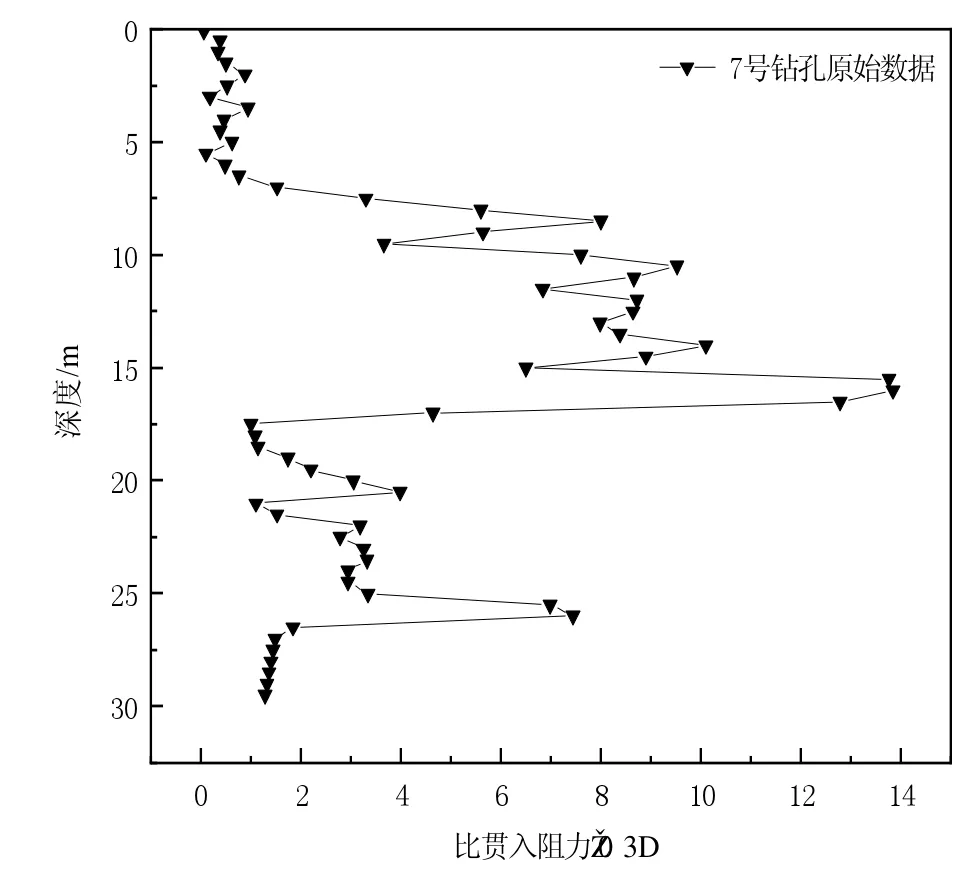
图2 比贯入阻力原始数据

选取该剖面6 组钻孔的比贯入阻力作为原始数据Y，沿深度方向维度为30/0.5=60，水平方向共计6 列数据维度为6，由此二维数组Y的维度为（30×6），即Mx1=30，Mx2=6。

确定完Y之后，结合场地信息预先定义场地参数，hx1，hx2表示剖面场地的深度和水平长度，hx1=30 m、hx2=113 m；ηx1，ηx2表示深度和水平方向上的数据间隔，ηx1=0.5 m、ηx2=1 m；则插值矩阵F的维度大小为hx1/ηx1=60，hx2/ηx2=113。在贝叶斯插值扩充后，每个钻孔沿深度方向的比贯入阻力有60 组数据，水平方向场地113 m 的间距转化为113 组矩阵的列向量，即插值矩阵F维度定义为（Nx1×Nx2=60×113）。Y作为插值矩阵的子集，6 列数据分别位于插值矩阵F的第0，23，45，70，93，112 列，后续将通过Y迭代计算，得到整个插值矩阵F的结果，从而实现数据扩充和预测未知区域比贯入阻力的目的。

3 插值结果分析

由前述可知本研究剖面已经转化为插值矩阵，将通过6 组原始数据Y进行贝叶斯插值，将一维的钻孔比贯入阻力数据进行扩充，通过迭代计算得到插值矩阵F，即可得到113 m 剖面上所有位置的土层比贯入阻力数据，实现一维到二维的数据扩充。

3.1 离散余弦矩阵

离散余弦矩阵（DCT）取Nx1=60，Nx2=113，分别带入表1 构建离散余弦函数Cx1（60×60），Cx2（113×113），计算结果如图3 所示，Cx1，Cx2分别表示沿深度和水平方向上的变换方阵。

图3 离散余弦矩阵Cx1，Cx2 计算结果

3.2 插值矩阵计算结果

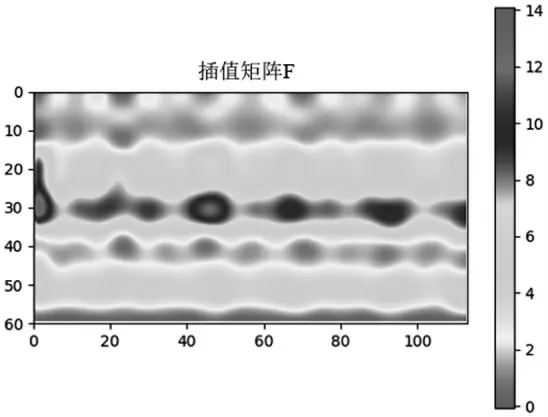
图4 插值后的比贯入阻力分布图

由图4可知，比贯入阻力在研究剖面上成带状分布，深度方向呈现波动变化的特征。在插值矩阵0~10行（实际深度0~20 m 处）比贯入阻力分布较为均匀，在0~3 MPa 之间；插值矩阵15~25 行（实际深度7.5~12.5 m 处）比贯入阻力分布在4~6 MPa 之间；在插值矩阵30 行（实际深度15 m 处）附近区域为比贯入阻力最大区域，尤其在0~5、40~50 列之间出现了比贯入阻力的最大值14.1 MPa。数据之间存在明显的分区域特征，为后续的土层划分工作提供了重要保障。

3.3 插值准确性验证

为了验证插值矩阵F的准确性，将地勘报告中的2 处未参与计算的钻孔数据的插值预测结果与该处真实的地勘数据进行比对，如图5 所示。

由图5可知，预测的插值曲线与原始数据较为吻合，整体走势也保持一致，在25~28 m 处个别点位略有偏差。这可能是由于钻孔不完全在二维垂直剖面内，钻孔不完全垂直于土层剖面，且土层的不确定性较高，插值后仍有可能出现小偏差的情况。从另一方面来说出现小部分点位偏差，可增强模型泛化能力，避免出现过拟合现象。

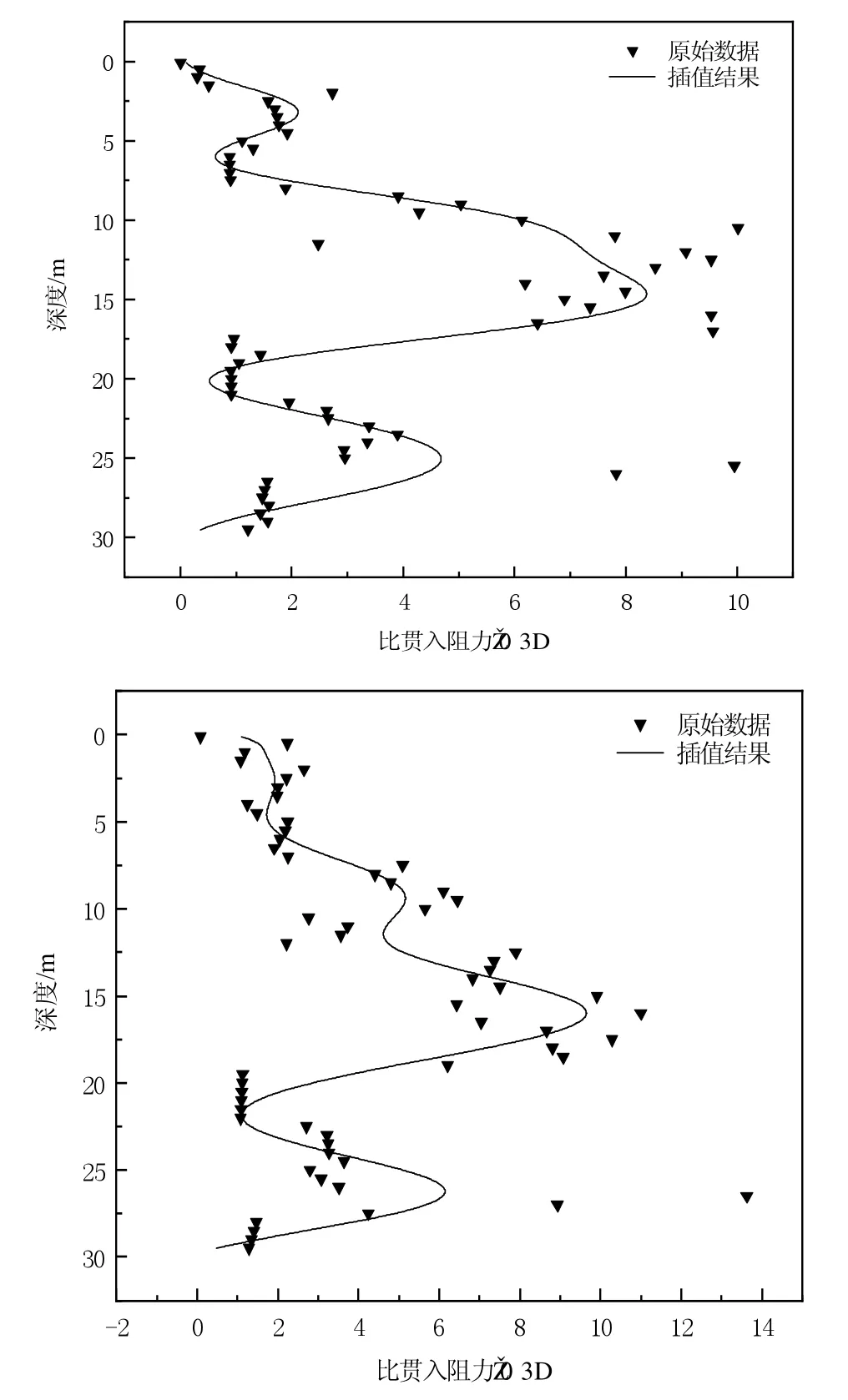
图5 插值结果与原始数据对比图

4 基于SVM 算法划分地层

4.1 SVM 原理

支持向量机SVM 是监督学习中一种常见的分类算法，SVM 在各种实际问题中都表现非常优秀。但是在工程勘察中，利用SVM 对地层进行划分的研究目前在国内外相对较少，本节将基于SVM 的强学习能力，结合周边场地的地勘数据，提出一种新的地层分类模型。

支持向量机的基本原理非常容易理解。如图6 所示，这是一组两种标签的数据，两种土层所包含的参数（本文采用的为比贯入阻力）分别由实心圆和空心圆代表。支持向量机的分类方法，是在这组分布中找出一个超平面（二维坐标系为直线）作为决策边界，使模型在数据上的分类误差尽量接近于0，尤其是在未知数据集上的分类误差（泛化误差）尽量小，对两种不同特征的数据进行有效的划分。因此，支持向量分类器又叫作最大边际分类器。

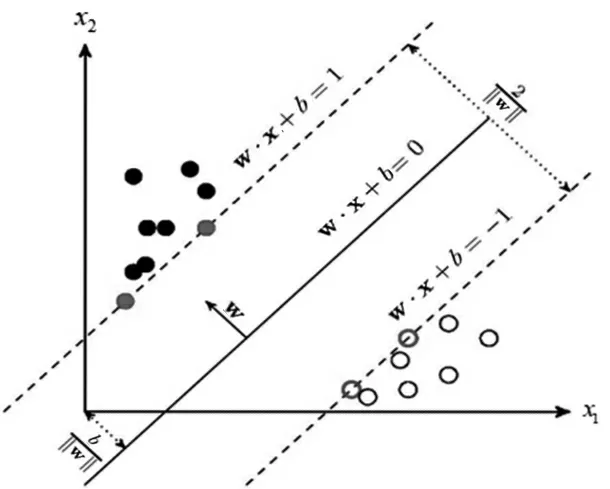
图6 SVM 原理图

4.2 周边场地数据收集

为了更好地适应本研究所在剖面地层的分布情况，做到具体问题具体分析，本研究搜集了部分周边场地的比贯入阻力与深度的地勘数据，以及对应数据点的地层名称，并绘制成散点图，如图7 所示。训练集数据的横纵坐标为比贯入阻力和深度，按照地层编号沿深度方向分布可分为7 类：填土、粘土、粉质粘土、粉土与粉砂、粉质粘土、粘土、粉质粘土。

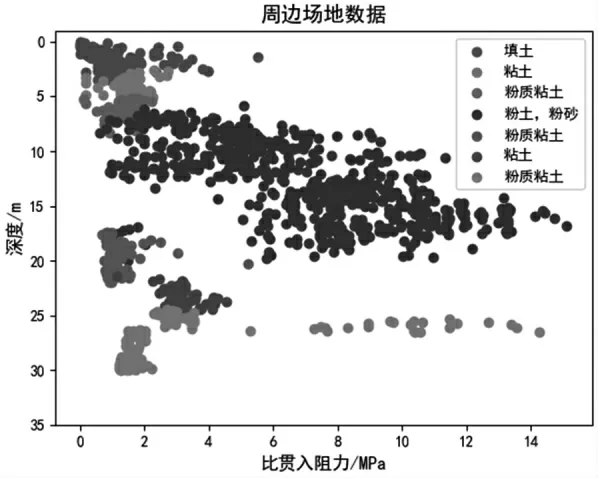
图7 SVM 训练集数据图

由图7可知，该地块土的类型主要分为7 类，在SVM 中，此数据集可看作7 分类的数据问题，找到6个超平面将数据进行划分。划分模型完成后，将第三节研究剖面计算得到的插值矩阵元素点带入模型，进行逐点的预测并画出地层剖面图。

4.3 地层划分结果

将场地周边数据分为3 列向量，前两列分别为每个数据点的深度、比贯入阻力，最后一列为该点对应的土层类型；然后将土层类型实例化，即将填土、粘土、粉质粘土、粉土与粉砂、粉质粘土、粘土、粉质粘土分别定义为数字1~7；最终将三列向量组合成矩阵形式作为训练集输入SVM 模型进行计算，结果如图8 所示。

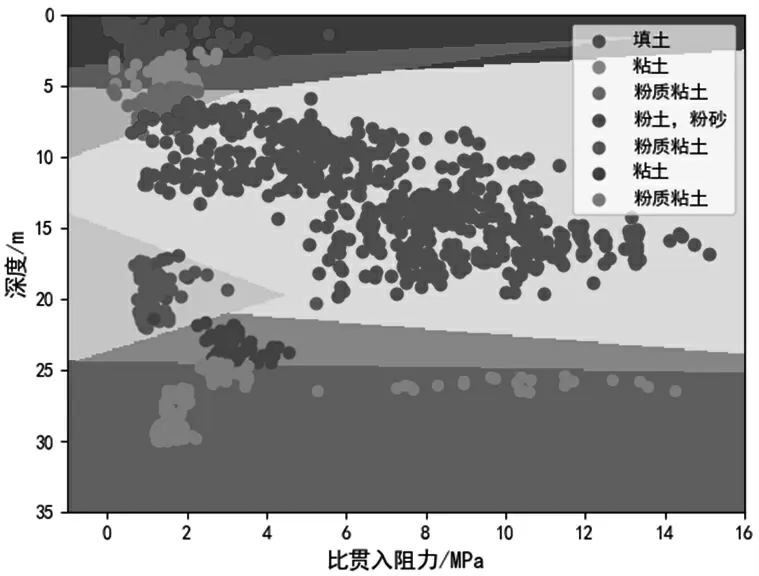
图8 SVM 分类结果图

由图8可知，本文用Python 将SVM 分类结果可视化，把16×35 的区域进行网格划分，不同颜色的区域内通过线性函数分割，分别代表不同的土层分类。分类结果准确率为95.56%，区域中心数据分类基本无误，但是由于数据量较大，且实测数据也可能出现误差，在边界处不可避免地出现数据交汇现象导致部分数据分类错误。分类模型建立后，将第三节的插值矩阵中6 780个像素点带入模型预测每一个像素点的分类，并画出二维散点图，如图9 所示。

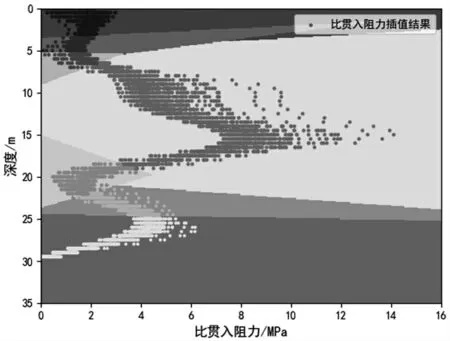
图9 线性核函数预测结果图

由图9可知，将研究场地的标贯击数插值结果带入分类模型后，6 780个数据点分别划分到不同颜色的区域当中，此时，每一个数据点都得到了相对应的土层编号1~7，从而完成了对插值数据的预测。最终将预测得到的土层编号作为像素点的颜色，得到地层划分剖面图，如图10 所示。

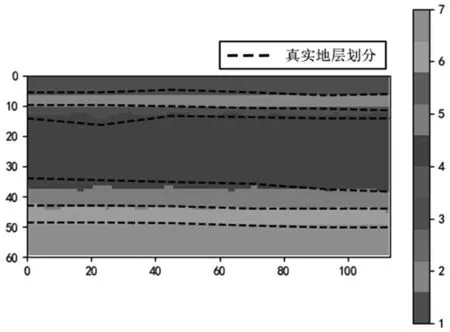
图10 地层剖面划分结果图

由图10可知，黑色虚线为地勘报告中所给出的地层划分线，在0~5 行为填土（编号1）、5~10 行为粘土（编号2）以及49~60 行为粉质粘土（编号7）分类效果非常准确；在15~30 列红色粉质粘土（编号3）的下边界、34~36 行粉色区域（编号5）的上边界存在多个像素点分类错误，考虑到此处地层有起伏，且位于不同地层的交界处，数据在此交汇较多，出现分类误差。总体地层的走势较为清晰。分类较为准确，但土层分界处的分类情况与真实地层分布还存在一定的差距。6 780个像素点分类准确的个数为6 448个，准确率为95.10%。

5 结论

本文以苏州蕾娜斯地块某场地勘察剖面为研究对象，通过对比贯入阻力数据进行贝叶斯插值，对整个剖面场地进行了地勘数据扩充。在插值结果的基础上利用支持向量机模型对插值后的数据进行分类，得到最终的地层剖面图。随后与实际的地层划分做出对比，计算了模型分类的准确率，主要结论如下。

（1）贝叶斯插值源于信号重建原理，对于土层这种离散性大，不确定性高的研究对象非常合适。切合工程实际，只需少量数据即可最大程度反推地层信息，提高了勘察结果的准确性。

（2）苏州蕾娜斯地块的比贯入阻力数据集有明显的分块特征，属于线性可分数据，支持向量机SVM 在处理线性分类问题时较其他算法表现更加优异，且加入了周边场地的地勘数据作为先验条件，大大加强了分类的准确性。

（3）本文采用的数据集是比贯入阻力，所提出的方法不仅仅适用于比贯入阻力一个物理量，涉及地层的任意物理量，例如标贯击数、内摩擦角等都可以进行插值扩充和地层划分。所以本文提出的模型具有一定的泛化能力，能够适应各类工程勘察项目，具有很强的实用性。