分级屈服型金属套管阻尼器减震理论与试验研究
吴 山,何浩祥,兰炳稷,陈建伟
(1. 北京工业大学工程抗震与结构诊治北京市重点实验室,北京 100124;2. 华北理工大学建筑工程学院,河北,唐山 063210)
金属屈服型阻尼器具有机理明确和性能稳定等优点[1],在结构减震设计中被广泛采用,其主要类型包括防屈曲支撑(BRB)、金属剪切耗能阻尼器、金属弯曲耗能阻尼器和铅阻尼器等[2]。防屈曲支撑减震性能突出且安装便捷,目前被广泛应用于减震结构。然而,其优异的性能是依靠核心单元塑性变形累积实现的[3],在反复拉压过程中会迅速累积塑性变形并产生明显残余位移[4−5],这不利于结构的快速修复。另外,核心单元位于约束单元内部,震后无法观察其损伤状态或单独更换,只能整体更换,可恢复性和经济性欠佳。金属剪切或弯曲耗能型阻尼器同样具有震后残余变形较大的不足,其耗能构件虽然外置,便于观察和单独更换,但其耗能钢板往往缺乏屈曲约束措施,容易屈曲失稳,性能并不稳定[6−7]。铅阻尼器塑性变形能力优越,性能稳定,在大变形循环过程中不会出现累积疲劳现象,但铅属于有毒重金属,铅泄露隐患制约了其应用[8]。针对上述问题,亟需设计一种性能稳定、易于安装和更换、且耗能状态可观察的金属屈服型阻尼器。研究者针对此需求进行了诸多有益探索。Amadeo[9]提出一种金属套管阻尼器,该阻尼器形似防屈曲支撑,依靠在外钢管上开洞形成的钢条充分耗能,性能稳定,耗能构件外置,在震后可以将耗损部分快速更换。然而,通过理论分析和拟静力试验建立的相关屈服位移和屈服荷载计算公式不够精确。李国强、孙瑛志等[10−11]从经济效益的角度将此种金属套管阻尼器与防屈曲支撑进行了比较,结果表明该阻尼器在用钢量上有明显优势。疲劳试验表明高宽比大的耗能钢条疲劳性能更优异,且可根据Manson-Coffin公式预测,但相关的整体设计公式和方法仍然不够准确,需要进一步探究。
此外,目前的金属屈服型阻尼器通常只针对中大震进行设计,在小震下难以屈服耗能,阻尼器为主体结构提供的附加阻尼较小,但提供了较大的附加刚度,减小了结构的周期,导致结构有可能遭遇更强烈的地震作用影响,这无疑是负面的。若阻尼器只针对小震设计,则在中大震下的耗能能力是不足的,因此,亟需提出一种能够在大中小震下均能有效耗能的阻尼器,即分级屈服型阻尼器。已有学者对分级屈服型阻尼器进行了理论和试验研究。陈云和蒋欢军等[12]提出一种环形分级屈服阻尼器,利用两种具有不同屈服位移的金属环实现阻尼器的分级屈服功能,但该阻尼器分级屈服效果不够显著,且占用空间较大。刘伟庆等[13]提出的新型分阶段屈服型软钢阻尼器和李国强等[14]提出的双阶屈服钢连梁联肢墙均采用将具有不同屈服位移的剪切型钢板和弯曲型钢板进行组合的方式来实现分级屈服功能的,原理为小震下剪切型钢板先屈服耗能,弯曲型钢板保持弹性,中大震下两种钢板共同耗能,然而,此种阻尼器构造复杂,对加工精度要求较高。高华国和张令心等[15]将Z型支撑和开孔腹板组合提出一种分级屈服复合型阻尼器,从构造和材料角度均可有效实现阻尼器分级屈服。但耗能构件容易滑移,滞回曲线不饱满。范圣刚等[16]提出的金属阻尼器通过将Q235钢和低屈服点钢结合并采用多种的开孔方式实现分级屈服。但通过低屈服点钢实现多级屈服提高了成本,制约了其工程应用。
有鉴于此,本文提出一种分级屈服型金属套管阻尼器,该阻尼器耗能机理明确,便于加工安装,耗能构件外置,易于观察构件损伤状态及单独更换,成本低廉。阻尼器耗能机理与文献[9 − 11]中的金属套管阻尼器类似,但本研究考虑了耗能钢条端部半刚性性能,对已有的屈服位移、屈服荷载计算公式进行了改进和修正,提出精度更高的计算公式,之后进行了拟静力试验,明确了该阻尼器的破坏特征,验证了其优良的耗能能力,并将理论计算、试验和有限元模拟结果进行了对比分析。
1 分级屈服型金属套管阻尼器的构造形式和工作原理
本文提出的分级屈服型金属套管阻尼器(Multistage yield metal tube damper, MYMTD)外形与防屈曲支撑类似,如图1所示,主要由内外钢管组成,外钢管四面开槽,形成耗能钢条和连接板,构成耗能模块,内钢管伸入外钢管内,通过焊接和螺栓连接实现内钢管与连接板固接,内外钢管端部带有端板和接头,与主体结构连接。当内外钢管发生轴向相对位移时,连接板带动耗能钢条发生剪切变形,屈服后耗能。为了实现分级屈服耗能功能,将耗能模块设置为两种,上下面和前后面各采用一种。两种耗能模块中耗能钢条的高宽比不同,高宽比小的钢条屈服位移小,中小震下即可屈服耗能,高宽比大的钢条屈服位移大,大震下方能屈服,从而实现分级屈服耗能的设计目标。可通过改变耗能钢条的高宽比、数量、厚度和材料性能有效调控MYMTD的各级屈服位移、屈服荷载等性能参数。
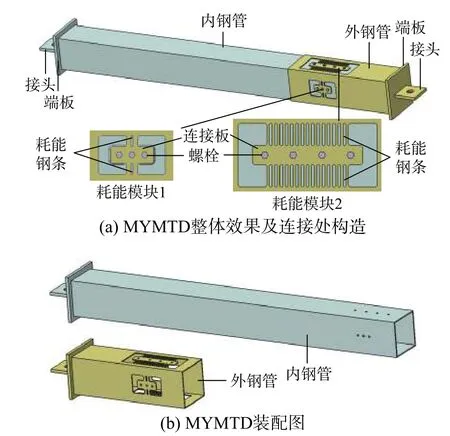
图1 MYMTD示意图Fig. 1 Schematic diagram of MYMTD
2 MYMTD性能参数的理论解析
针对已有的单级屈服金属套管阻尼器的设计理论精度不足的局限,本文力求通过理论解析和试验数据拟合的方式得到MYMTD的各级刚度、屈服荷载和屈服位移的设计公式。首先考虑端部半刚性影响,推导耗能钢条初始刚度,进而得到MYMTD整体刚度。之后推导MYMTD的屈服荷载计算公式,进而获得了精度较高的屈服位移设计公式。
MYMTD可视为由内钢管、耗能模块和外钢管串联形成的等效模型[17−19],如图2所示。命名外钢管四个面上的耗能模块为耗能模块1、耗能模块2、耗能模块3和耗能模块4。

图2 MYMTD简化模型Fig. 2 Simplified model of MYMTD
首先对MYMTD的弹性刚度进行求解。为防止应力集中,对耗能钢条进行倒角设计,具体构造如图3所示。理论分析时对其进行等效处理,如图3(b)所示,等效耗能钢条高度可表示为:
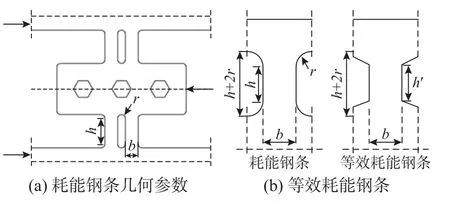
图3 耗能钢条示意图Fig. 3 Schematic diagram of energy dissipation steel strip

式中:h′为等效耗能钢条高度;h为实际耗能钢条高度;r为倒角半径。
下面先假定耗能钢条两端固接,求解耗能钢条弹性刚度,再考虑半刚性节点的影响,对刚度进行修正。单个耗能钢条受到剪力和弯矩共同作用,计算模型如图4所示。以耗能模块1的耗能钢条为例(其参数均标有下标1),其弯曲变形计算公式为:
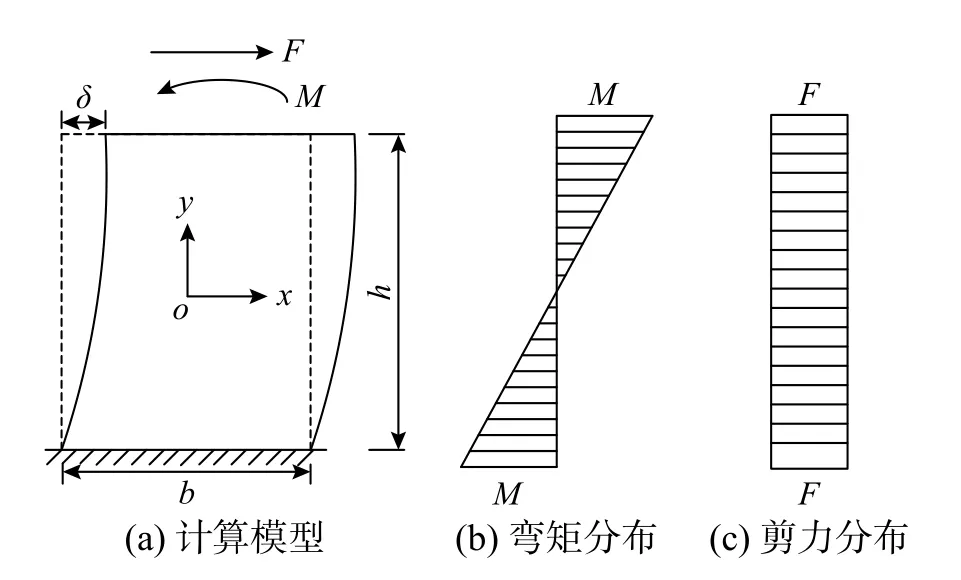
图4 耗能钢条计算模型Fig. 4 Computation model of energy dissipation steel strip
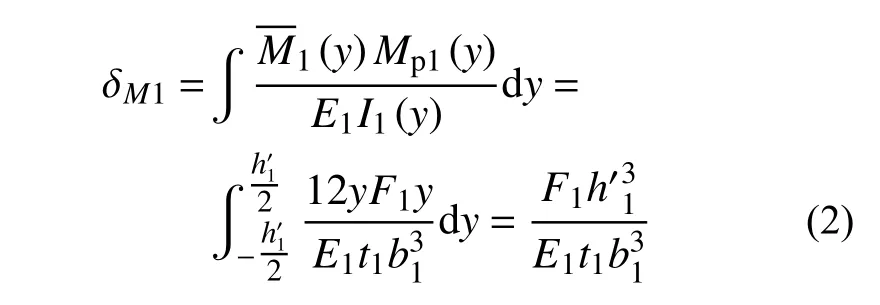
式中:F1为水平外荷载;y为y轴坐标;M1(y)为单位荷载下任一截面的弯矩,(y)=y ;Mp1(y)为水平外荷载F1作用下的任意截面弯矩,Mp1(y)=F1y;E1为钢材的弹性模量;I1(y)为任一截面的惯性矩,I1(y)=t1/12;b1和t1为耗能钢条的宽度和厚度。
耗能钢条的剪切变形为:

式中:β1为剪力不均匀系数,对于矩形截面取1.2;(y)为单位荷载下任一截面的剪力,(y)=1 ;Vp1(y)为水平外荷载F1作用下的任意截面剪力,Vp1(y)=F1;A1(y)为任一截面面积,A1(y)=t1b1;G1为钢材剪切模量,泊松比ν=0.3时,式(3)可表示为:

故耗能钢条的剪切变形可表示为:

由此可得耗能钢条弹性刚度计算公式为:

实际上,耗能钢条两端并非完全固接,当耗能钢条变形时,连接部位也会随之发生变形,这会使耗能钢条的刚度减弱,因此本文引入刚度折减系数对其进行修正,修正后的耗能钢条弹性刚度可表示为:

式中,K1和γ1为修正后耗能模块1中耗能钢条的弹性刚度和刚度折减系数。
从文献[9]和文献[11]的试验结果来看,耗能钢条的高宽比对刚度折减系数存在明显影响,选取文献[9]中试件TTD15/20/5、TTD20/20/5和文献[11]中试件1-1、2-1、3-1的弹性刚度进行拟合从而确定刚度折减系数取值,得到拟合公式为:

拟合相关系数为0.94,方差为0.0082,拟合效果如图5所示。
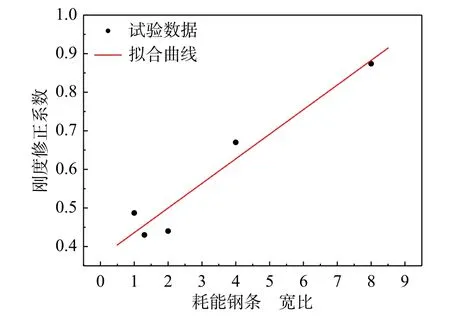
图5 刚度折减系数拟合效果Fig. 5 Fitting effect of stiffness reduction coefficient
为了进一步验证耗能钢条弹性刚度计算公式的正确性,将文献[9]和文献[11]的试验结果与由理论公式得到的计算结果进行对比,参见表1。可见误差均在10%以内,理论公式合理有效。

表1 试验结果与本文理论结果对比Table 1 Comparison of experimental results in comparison with theoretical results in this paper
耗能模块1上所有耗能钢条的总弹性刚度为:

式中,n1为耗能模块1上耗能钢条总数。
可按上述方法求得四个耗能模块的弹性刚度,记为Kw1、Kw2、Kw3和Kw4,四者为并联关系,采用上标表示性能参数的阶数,可知四者总一阶刚度(弹性刚度)为:
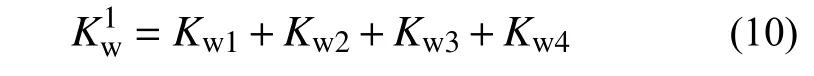
设耗能模块1和耗能模块2(一组对面内)先发生屈服,耗能模块3和耗能模块4(另一组对面内)未屈服,此时四个耗能模块的二阶刚度为:

式中,α1和α2为耗能模块1和耗能模块2的屈服后刚度系数。
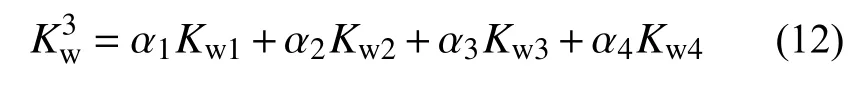
式中,α3和α4为耗能模块3和耗能模块4的屈服后刚度系数。
外钢管受轴向拉压荷载,其弹性刚度公式为:

式中:KE为外钢管弹性刚度;EE为外钢管钢材弹性模量;AE为外钢管横截面积;lE为外钢管长度。
内钢管受力状态与外钢管相同,其弹性刚度公式为:

式中:KI为内钢管弹性刚度;EI为内钢管钢材弹性模量;AI为内钢管横截面积;lI为内钢管长度。
外钢管、耗能模块和内钢管为串联关系,由式(10)、式(13)和式(14)可得MYMTD的一阶刚度K1(弹性刚度)为[20]:
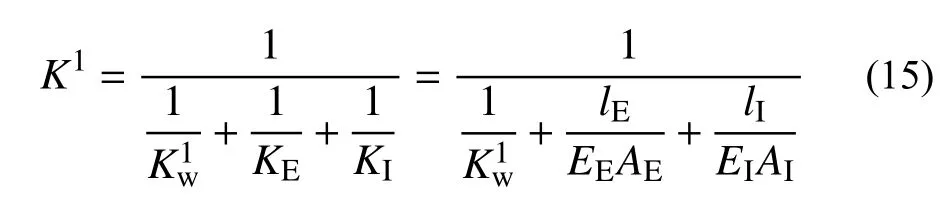
将耗能模块的二阶刚度和三阶刚度代入式(15)可得MYMTD的二阶刚度K2和三阶刚度K3:

耗能模块为MYMTD的主要耗能构件,设计时应保证耗能模块在设计位移内发生屈服,且内外钢管保持弹性状态。耗能钢条横截面在外荷载作用下产生切应力和正应力,两者之一达到强度条件耗能钢条即发生屈服。耗能模块1内的单个耗能钢条最大剪应力τ1可表示为:


式中,fy1为钢材屈服强度。进而可以求得耗能模块1的耗能钢条发生剪切屈服时的屈服荷载Fy1v为:
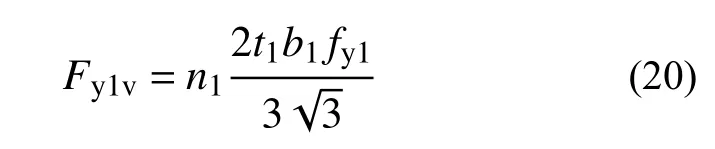
耗能模块1上的单个耗能钢条最大正应力σ1可表示为:

式中,Wz1为弯曲截面系数,z代表截面中性轴,矩形截面为Wz1=tb2/6。正应力强度条件为:
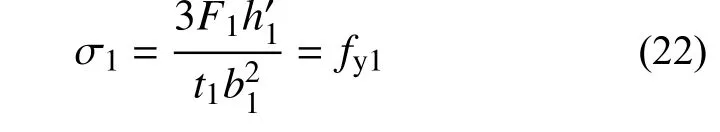
由此可得耗能模块1上的耗能钢条发生弯曲屈服时的屈服荷载Fy1m为:

基于式(20)和式(23)可得耗能模块1上的耗能钢条的屈服荷载Fy1w为:

外钢管四个耗能模块的耗能钢条屈服荷载均可用此方法计算。
四个耗能模块为并联关系,设耗能模块1和耗能模块2(一组对面内)先屈服,则MYMTD的一阶屈服荷载为:

耗能模块3和耗能模块4(另一组对面内)屈服时MYMTD的二阶屈服荷载为:


综上,本文推导了MYMTD的各级屈服位移和屈服荷载的精确公式,相关理论也可以为传统金属阻尼器的设计提供有效支持。下文将通过试验和有限元分析方法对理论结果的精确性进行验证。
3 试验研究
为验证理论公式的正确性,制作一个MYMTD的耗能段试件,并进行了拟静力试验。文[11]中关于套管式金属阻尼器疲劳性能的结论适用于MYMTD,因此本文未对其疲劳性能进行研究。
3.1 材性试验
MYMTD试件采用同批次的Q235B钢,根据《金属材料室温拉伸试验方法》(GB/T 288.1−2010)制作拉伸试件,进行材料的单轴拉伸试验,得到的材料屈服强度fy、抗拉强度fu、收缩率A、伸长率δ和弹性模量E参见表2。

表2 试件钢材力学性能Table 2 Mechanical properties of steel
3.2 试件设计
为了充分验证MYMTD的多级屈服特性,设计的两种耗能钢条高宽比差距较大,分别为2和8。高宽比越大,其屈服位移越大且承载力和刚度越低。为防止高宽比为8的耗能钢条出力过小,其数量设置的较多。内外钢管厚度均8 mm,开洞倒角半径均6 mm。为避免内外钢管间摩擦力过大,在其间涂抹润滑脂。试件的正视图和俯视图如图6所示。制造MYMTD时,首先在外钢管上开洞,形成由耗能钢条和连接板构成的耗能模块,再将内钢管伸入外钢管内部,最后通过螺栓和焊接的方式将连接板和内钢管固接。
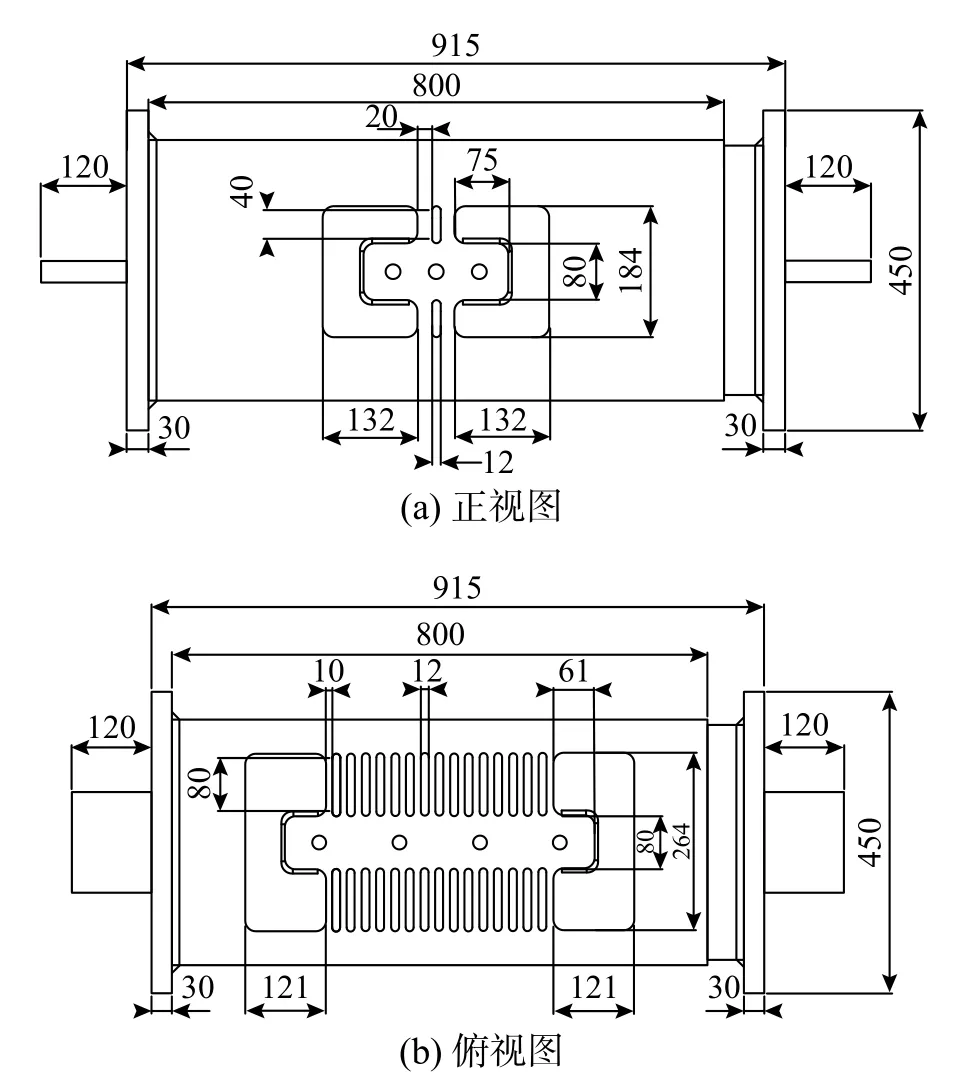
图6 试件构造及尺寸 /mmFig. 6 Details and dimensions of specimen
3.3 加载装置和加载制度
采用MTS疲劳实验机进行阻尼器试件的拟静力试验。将试件竖向放置,其两端的接头通过夹具与疲劳试验机连接,夹具与试件接头接触面摩擦系数较大,且施加足够的预紧力,因此不会出现滑移,下端固定,上端施加拉压荷载,试验装置如图7所示。使用加载设备自带的采集位移荷载功能记录试验数据。
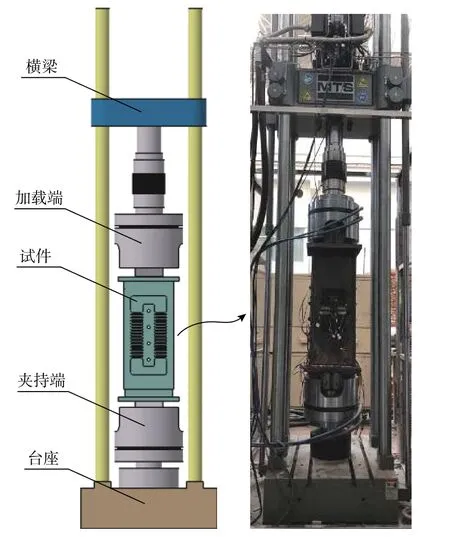
图7 试验装置Fig. 7 Experiment device
根据《建筑抗震试验规程》(JGJ/T 101−2015)规定,首先采用力控制加载,从40 kN开始,以5 kN为单位递增,直至找到一阶屈服点为止,之后改用位移控制加载,从4开始,以4为单位递增,20以内每级位移加载一圈,20开始每级加载两圈,当恢复力下降至85%峰值恢复力时停止加载,如图8所示,加载频率0.01 Hz。

图8 加载时程Fig. 8 Loading time history
3.4 试验现象
试验初期,试件无异响,加载至70 kN时,出现一阶屈服点,小高宽比钢条端部应变数据如图9所示,结合由表2数据可知,此时钢材应变已达到屈服应变0.0013,相应的一阶屈服位移为0.5 mm。采用位移控制加载至10 mm时,试件恢复力达到峰值。12 mm位移下正向加载时,高宽比小的耗能钢条两端出现裂缝,如图10(a)所示,另一种耗能钢条完好,此时滞回环依然饱满,但承载力出现轻微下降,反向加载时,裂缝贯通,高宽比小的耗能钢条剥落,如图10(b)所示。图中白色斑点是为视觉技术测量变形而喷涂的标记,对试验结果不造成影响。承载力急剧下降至85%以下,停止加载。
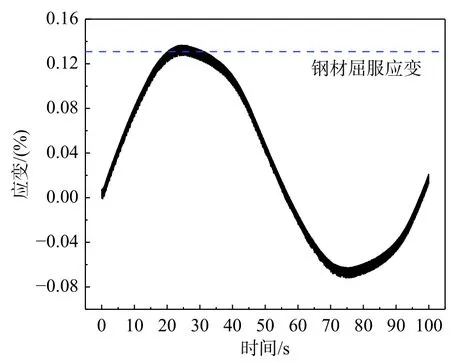
图9 小高宽比钢条屈服时端部应变Fig. 9 Strain at end of strip with small height-width ratio at yielding

图10 耗能钢条破坏Fig. 10 Failure of energy dissipation steel strips
3.5 试验结果分析
3.5.1 滞回曲线和骨架曲线
图11给出了试件的滞回曲线和骨架曲线。滞回曲线整体饱满,内外钢管没有明显的屈曲和面外变形,屈服后刚度没有随着加载圈数增多而出现明显下降,在耗能钢条开裂前,承载力没有下降,表明MYMTD具有优越的变形能力和耗能能力。加载至12 mm第一圈时,高宽比小的耗能钢条出现裂缝,而高宽比大的耗能钢条没有明显破坏,说明耗能钢条高宽比越大,其疲劳性能越好。

图11 滞回曲线和骨架曲线Fig. 11 Hysteretic curve and skeleton curve
3.5.2 屈服荷载与屈服位移
提出MYMTD构造的主要目的是使两种耗能钢条具有不同的屈服位移从而实现分级屈服。为了验证MYMTD具有一阶屈服的能力,给出加载75 kN和2 mm时的荷载-位移曲线,如图12所示。由图12(a)可见此时已出现滞回环,证明一阶屈服位移是存在的。从图11中可以看出二阶屈服位移较为明显。由此验证了MYMTD具备分级屈服能力。
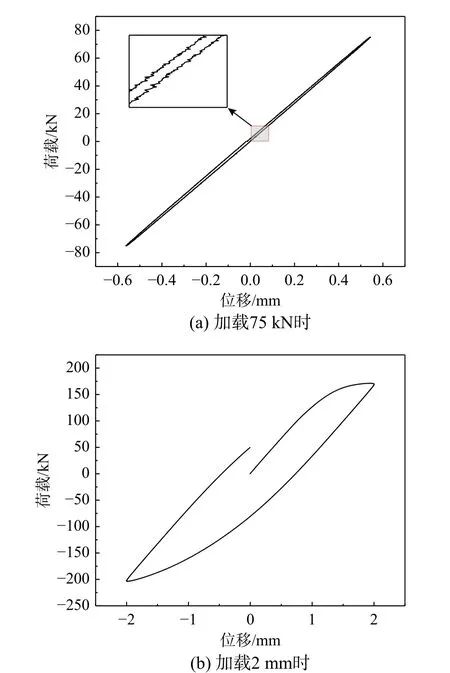
图12 加载75 kN和2 mm时的荷载-位移曲线Fig. 12 Load-displacement curve under 75 kN and 2 mm load
表3给出了试件的屈服位移和屈服荷载。从表3可以看出,试件一阶屈服位移和二阶屈服位移差别显著,可以较好地实现不同位移下均可耗能减震的设计目标。

表3 试件屈服荷载和屈服位移Table 3 Yield load and yield displacement of specimen
3.5.3 刚度退化
采用同级位移下的环线刚度Kj研究试件的刚度退化。试件刚度退化曲线如图13所示。加载初期,刚度急剧退化,随着加载位移幅值加大,刚度退化愈发平缓。加载至12 mm试件破坏时,环线刚度退化至初始环线刚度的11.76%。整体刚度退化曲线较为平滑,没有明显突变,表明MYMTD力学性能稳定,具有较出色的变形能力。
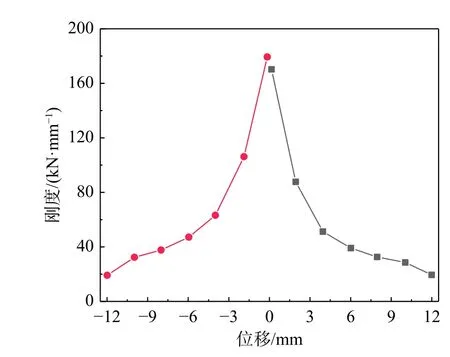
图13 刚度退化曲线Fig. 13 Stiffness degradation curve
3.5.4 耗能能力分析
等效粘滞阻尼比可以有效量化阻尼器或构件的耗能能力[21]。MYMTD试件的等效粘滞阻尼比如图14所示。可见试件的等效粘滞阻尼比随位移增大而增大,初始阶段增大速度较快,4 mm位移后增大速度逐渐趋于平缓,破坏时达到最大。试件的最大等效粘滞阻尼比高达0.46,表明MYMTD试件在大位移下仍具有优良的耗能能力。

图14 等效粘滞阻尼比Fig. 14 Equivalent viscous damping ratio
4 有限元分析
4.1 有限元模型
为了进一步验证理论和试验的结果和结论,本文采用ABAQUS/Standard分析模块对试件进行了模拟分析。所有部件的单元均采用壳单元(S4R)模拟,试件有限元模型如图15所示。

图15 MYMTD试件有限元模型Fig. 15 Finite element model of MYMTD specimen
内外钢管之间设置表面接触,耗能模块连接板与内钢管接触面绑定(Tie)约束,在接头外设参考点(RP1),参考点与接头耦合,采用位移加载方式,对参考点RP1施加z方向逐级增大的往复位移,加载时程保持与试验一致,钢材采用双线性随动强化模型模拟。
4.2 模型验证
对拟静力试验进行模拟,与试验对比结果如图16所示。

图16 试验与模拟结果对比Fig. 16 Comparison of experimental and simulated results
由结果可知,一阶屈服点小高宽比钢条屈服,二阶屈服点大高宽比钢条屈服,不同高宽比的耗能钢条具有不同的屈服点,验证了MYMTD的设计理念,有限元模拟结果与试验结果吻合较好,特别是初始刚度、屈服点和卸载刚度与试验结果均非常接近,但屈服后刚度与试验结果存在一定差异,原因在于有限元模型采用的双线性随动强化模型与钢材实际性能有一定区别。
为验证MYMTD具有分级屈服特性,提取位移为0.515 mm(一阶屈服位移左右)和0.812 mm(二阶屈服位移左右)时的有限元模型Mises应力云图,如图17所示。从图17中可见,当位移为0.515 mm时小高宽比耗能钢条两端已经屈服,而大高宽比耗能钢条尚处于弹性阶段;当位移为0.812 mm时,两种耗能钢条均已屈服,从而验证了MYMTD具有分级屈服特性,且高宽比越小的耗能钢条屈服位移越小,应力水平越高,疲劳性能越差。另外,MYMTD工作时应力集中在耗能钢条两端部位,这与试验时耗能钢条两端先出现裂缝并断裂的现象是相互印证的。

图17 应力云图 /MPaFig. 17 Stress nephogram
4.3 理论、试验与模拟对比
将理论计算、试验和有限元模拟得到的试件一阶性能参数列于表4。

表4 性能参数理论计算、试验和有限元模拟结果对比Table 4 Comparison of performance parameters obtained by theoretical calculation, experiment and finite element simulation
以试验结果为基准计算了理论结果和模拟结果的误差,其中计算二阶屈服刚度时α1和α2取0.81,计算三阶屈服刚度时α1、α2、α3和α4均取0.02。由表4可以看出,理论计算和有限元模拟得到的一阶和二阶性能参数与试验结果吻合较好,误差均在10%以。虽然有限元模拟中三阶刚度结果偏大,但对整体滞回效果影响不大。总体来看,理论计算公式与模拟方法是正确和合理的。
5 结论
本文提出了一种分级屈服型金属套管阻尼器,通过两种不同高宽比的耗能钢条具有不同屈服位移的原理实现阻尼器的多级屈服特性。由理论推导得到了该阻尼器的性能参数。通过拟静力试验对理论公式进行了验证,并研究了阻尼器的破坏模式、滞回性能、刚度退化特性及耗能能力。最后通过有限元精细化模拟进一步与理论和试验结果进行对比验证。具体结论如下:
(1)不同高宽比的耗能钢条具有不同的屈服位移,本文提出采用两组不同高宽比的耗能钢条作为耗能构件的阻尼器可以有效实现分级屈服功能。
(2)耗能钢条间开洞处倒圆角处理后耗能钢条两端应当做半刚性节点处理,对钢条的刚度存在削弱现象,引入刚度折减系数可以有效修正刚度。本文提出的阻尼器性能参数计算公式具有较高精度,可以准确预测耗能模块和阻尼器整体性能,也为其它类型的金属阻尼器性能参数计算提供参考。
(3)该阻尼器整体性能稳定,具有较好的变形能力和耗能能力。阻尼器应力集中部位在耗能钢条两端,循环荷载作用下,耗能钢条两端先产生裂缝,裂缝贯通后发生破坏。高宽比小的耗能钢条屈服位移更小,刚度更大,疲劳性能更差,在设计和制造时要注意安全校核。
(4)有限元模拟得到的滞回曲线与试验结果吻合较好,应力集中部位和试验现象一致,验证了本文建模方法的合理性和正确性。
(5)为了进一步验证阻尼器的性能,可以对安装有传统单级阻尼器和分级屈服阻尼器的结构进行弹塑性时程分析和性能比对,但限于篇幅本文没有深入探究,将在以后的研究中开展。

