Polymer-/Ceramic-based Dielectric Composites for Energy Storage and Conversion

Honghui Wu , Fangping Zhuo* , Huimin Qiao , Lalitha Kodumudi Venkataraman ,Mupeng Zheng, Shuize Wang*, He Huang*, Bo Li, Xinping Mao, and Qiaobao Zhang*

1. Introduction

Dielectric composite materials are usually produced from at least two constituent dielectric materials with notably different functional properties, such as electrical or mechanical properties, wherein one typical dielectric is chosen as a matrix and a dielectric material is chosen as filler,combining the unique properties of both components.[1]Generally,organic polymers and inorganic ceramics can both be used as matrix materials and/or fillers in the fabrication of a dielectric composite. For nonpolar polymers such as polytetrafluoroethylene and low-density polyethylene, the dipoles cancel out each other due to symmetry,resulting in lower dielectric permittivity,[2,3]whereas for polar polymers like poly(vinylidene fluoride) (PVDF),[2,4]the dipole movements do not cancel out each other and exhibit higher dielectric permittivity than that of polymers without polar orders. Apart from polymers,nonconducting and(semi-)conducting ceramics are now widely utilized to prepare polymerbased and ceramic-based dielectric composites.[5–11]Nonconducting ceramics are usually considered insulators as they exhibit a high band gap such as Pb(ZrxTi1−x)O3(PZT) piezoceramics,[5]prototypical ferroelectric (FE)BaTiO3(BT),[6,7]and SrTiO3.[8]In addition,conducting fillers including graphene[9]and carbon nanotubes,[10]and semiconducting ZnO particles[11]are also widely used since they possess some merits. For example, comparatively higher dielectric permittivity can be simply achieved via the addition of conducting ceramic fillers, although one of the demerits is that the addition of conducting fillers is very limited because continuous channels are formed after the critical concentration.[12]

The growing demand for environmentally friendly, highly efficient, and low-cost energy storage and conversion is spurred by plenty of applications in electric vehicles, energy or power systems, and smart microelectronics devices. Dielectric composites are now rapidly emerging as novel materials in advanced electronic devices and energy systems including capacitive energy storage and energy harvesting,[6,7,13–18]high-power electronics,[11,19]solid-state cooling devices,[20–24]electric circuits, and[25]actuators and sensors (see Figure 1).[26–31]To meet the demands of the industry and advanced energy systems, polymer- and ceramic-based dielectric composites with high dipole reversibility show great application potentiality.Polar polymers (i.e., PVDF and its copolymers) and polar ceramics (i.e., piezoelectrics and ferroelectrics) are provoking many research activities in dielectric composites for energy storage and conversion technologies.[6,7,11–31]In the past two decades, polymer-/ceramic-based dielectric composites containing piezoelectricity and ferroelectricity have been intensively developed for high-performance energy and power systems.[1,6,7,11,13–31]For instance, a discharged density above 30 J cm−3and a giant electrocaloric temperature change up to about 50 K near room temperature have been realized in PVDF-based FE nanocomposites,[15,22]and significantly enhanced depolarization temperature and mechanical quality factor have also been achieved in ceramic-based semiconductorrelaxor FE composites.[11]In addition to the great strides in experimental research, it is useful and in strong demand for predicting the properties of dielectric composites. Early attempts have been tried to theoretically understand the properties of dielectric composites, such as dielectric permittivity,[32–37]piezoelectric coefficient,[38]and hysteresis effect.[39]Comprehensive finite-element phase-field simulations and machine learning frameworks have been developed to predict the breakdown behavior, damage evolution, and electromechanical properties of dielectric composite systems.[40–42]The development of both theoretical tools and experimental protocols helps in better understanding of the dielectric composite systems, and much progress has been achieved in the last 10 years.

In this review, we begin with a summary of a brief history of the development of dielectric composites, followed by an overview of the basic electrical and mechanical parameters for evaluating the relevant functionality of dielectric composites. Then, recent advances in polymer- and ceramic-based dielectric composites are highlighted,followed by a discussion on fabrication techniques for highperformance dielectric composites. Viewpoints regarding the challenges and future research opportunities in high-performance polymer- and ceramic-based dielectric composites are discussed, and the conclusion and outlook are highlighted in the last section of this review.

2. Brief History of the Development of Dielectric Composites

The development of dielectric composites is closely related to the progress in subgroups of dielectrics such as piezoelectric and FE materials. Piezoelectricity was first discovered in quartz and Rochelle salt crystals,[43]which is characterized by a linear coupling between mechanical strain and polarization. Piezoelectric materials have been commercially used for electromechanical energy interconversion.[28]FE materials are a subgroup of piezoelectrics. Valasek discovered ferroelectricity in 1920 and then experimentally confirmed the piezoelectric response and polarization hysteresis loop.[44,45]FE materials possess at least two energetically equivalent spontaneous polarization states, and these two directions of spontaneous polarization are capable of being switched between each other by experiencing an electric field. Most piezoelectric devices used in ultrasound imaging are FE materials such as PZT ceramics.[28]The PZT system was first developed at the Tokyo Institute of Technology in 1952, which exhibits anomalously superior dielectric and piezoelectricresponses when the selected compositions are at a morphotropic phase boundary.[46–48]However, the high density(～7.9 g cm−3) and brittle nature of PZT ceramics also limit their practical application in flexible electronics. This triggers the researchers to search for flexible and lightweight organic polymers with outstanding piezoelectricity.[49–51]For example, in 1969, Kawai discovered piezoelectricity (a piezoelectric charge coefficient of 20 pC N−1) in PVDF,[49]which is lower than the counterpart ceramic-based piezoelectric materials.Hereafter,different approaches were proposed to access the high piezoelectric response of PVDF such as introducing voids into polymers, optimizing poling process, and improving crystal orientation via the addition of trifluoroethylene (TrFE).[52,53]PVDF, as well as its copolymers, is of greatest interest as piezoelectric polymers so far,and the progress in piezoelectric coefficients of polymers is summarized in recent reviews.[54,55]Even if the piezoresponse of the state-of-the-art polymers is not so high as that of piezoceramics,polymers still merit unique properties that ceramics do not possess,such as their low weight, mechanical flexibility, smaller acoustical impedance,and lower fabrication cost.

Hong Hui Wu is currently an associate professor at the University of Science and Technology Beijing. He received his Ph.D. degree from the Hong Kong University of Science and Technology. His research interests mainly are advanced metal materials, integrated computational materials engineering, and materials informatics. Till now, he has published more than 80 papers, including Nature Communications, Materials Today,Chemical Society Reviews, etc., sixteen of which are highly cited, which attracted more than 2500 citations with an h-index of 26.

Fangping Zhuo is a postdoctoral researcher at the Department of Materials and Earth Sciences, Technical University of Darmstadt, Germany. He received his Ph.D. degree in Chemistry from Tsinghua University, Beijing, China. For his PhD thesis, he visited the Group for Ferroelectrics and Functional Oxides in the Institute of Materials of Swiss Federal Institute of Technology in Lausanne (EPFL) for six months. He was a postdoctoral researcher at the Department of Physics, Korea Advanced Institute of Science and Technology (KAIST). His research interests are (anti-)ferroelectric materials, machine learningbased piezoresponse force microscopy technique, and dislocation-tuned functionalities of ferroelectrics.

Huimin Qiao is a research professor at the Department of Advanced Materials Science and Engineering at Sungkyunkwan University (SKKU), Korea.She received her Ph.D. in Materials Physics and Chemistry from Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences. Her research interests include ferroelectric materials and the application of scanning probe microscopy on ferroelectrics.

The concept of designing dielectric composites by taking full advantage of both ceramic and polymer for achieving better performance and flexibility dates back to the earlier 20th century.In 1972,Kitayama and Sugawara reported the first flexible 0-3 type PZT–PVDF piezoelectric composite with a combination of an active PZT ceramic filler in a passive PVDF matrix,[56]which demonstrated enhanced piezoelectric and dielectric performances compared with pure PVDF. Then, Newnham et al.[57]first proposed the concept of connectivity,which also included 10 connectivity families for a diphasic composite (Figure 2). In Table 1, we summarize the brief history of developing typical dielectric/piezoelectric/ferroelectric composites. Before the 21st century,enormous efforts were made to develop Pb-based ceramicpolymer piezoelectric composite materials for sensors and transducers, mainly focusing on the design of connectivity and processing techniques.[58,59]Over the past 20 years of this century, Pb-free polymer-based FE nanocomposites possessing outstanding properties,namely,high intrinsic dielectric permittivity and electrical breakdown strength, are attracting ever-increasing interest driven by the potential applications in capacitive energy storage,[14,15]energy harvesting,[13]and solid-state cooling.[20,22]The advances in nanocomposites containing the FE polymer for high efficient energy storage applications are well-summarized in recent reviews.[15,60]

The discussion of dielectric composites was taken beyond polymerbased composites to include ceramic–ceramic composites such as relaxor–FE composites[30,44]and FE–antiferroelectric (AFE) composites.[61,62]Ceramic–ceramic FE composites are now “hot” topics,despite that the first article was published in 1980, when an FE–AFE composite was fabricated by designing FE and AFE layers.[61]Later,Dausch et al.[39,63]revealed that an FE phase in an AFE matrix can reduce the field-induced phase transition critical field. Lee et al.[64,65]demonstrated phase transformation induced by a low field in Pb-free relaxor–FE (RE–FE) composites, where RE and FE phases are served as matrix and filler,respectively. Recently, the RE–FE composite approach is a solution in the quest for large strain achieved at low fields in leadfree incipient piezoceramics.[66]The recent interest in FE ceramic–ceramic composites was fueled by the reports of the enhancements of depolarization temperature and mechanical quality factor in 0-3 type semiconductor–relaxor FE composites.[11]In addition, the ceramic–ceramic composite strategy has been widely used to modulate specific properties, for example, dielectric permittivity,[30,67,68]piezoelectric properties,and[69]electromechanical properties.[31]

Lalitha Kodumudi Venkataraman (a.k.a Lalitha K.V.; https://orcid.org/0000-0002-4848-5436)is currently a Group Leader at Technical University of Darmstadt, Germany. Her recent research interests are on developing and characterizing leadfree piezoceramics with a focus on quenching perovskite-structured bismuth-based ferroelectrics. She is the Principle Investigator of the Deutsche Forschungsgemeinschaft funded project on “Quenching enhanced lattice polarizability in leadfree ferroelectrics” (grant no. KO 5948/1-1, Nr. 414311761).She finished her doctoral studies at the Indian Institute of Science, Bangalore, India. She is also the recipient of the Alexander von Humboldt Postdoctoral Fellowship (2016-2018) and the Electroceramics 2020 Young Researcher Award.

Mupeng Zheng was born in China in January 1988. He received his Ph.D. degree at Beijing University of Technology, Beijing, China in 2015. He is currently an associate professor at the Beijing University of Technology. His research interests are ceramic processing, ferroelectric, and piezoelectric properties of ferroelectric ceramics as well as their application in energy harvesting devices.

3. Basic Electrical and Mechanical Parameters of Dielectric Composites

Regarding various energy storage and conversion applications, the following basic electrical and mechanical parameters will be introduced,including dielectric permittivity and loss, dielectric nonlinearity, polarization, electrical and thermal conduction, piezoelectric coefficient,breakdown strength, mechanical quality factor, electrocaloric temperature change,energy storage density,and efficiency.Other electrical and mechanical parameters (elastic constants, Young’s modulus, and depolarization temperature)are also important to evaluate the material property and device performance; we directly highlight some parameters that are related to the energy performance in the corresponding sections.

3.1. Electrical Polarization and Dielectric Response

Dielectric permittivity is usually described as the relative permittivity of a matter in comparison with the free space.In general,the macroscopic polarization(Pi)is the sum of all dipole moments,which can be calculated via the following equation:

where ϵ0refers to the vacuum permittivity, Ejdenotes the applied electric field, and χijmeans the dielectric susceptibility. It is welldocumented that polarization and dielectric displacement (Di) are interrelated as follows: Di= ϵ0Ej+ Pi. The dielectric permittivity is composed of real (ϵr) and imaginary (ϵi) parts, and the dielectric loss is defined as tanδ = ϵi/ϵr, which describes the power loss in a dielectric material. Dielectric materials usually have four main polarization mechanisms (i.e., interfacial and space charge,dipolar, ionic, and electronic) in the resonance and relaxation regions (Figure 3a).[2]The electronic polarization is related to the displacements of the electrons with reference to the nucleus,whereas the ionic polarization is a result of electric field-driven movements of the positive and negative ions (Figure 3b), respectively. The dielectric loss caused by either the electronic polarization or ionic polarization mechanism is negligible due to the ultrahigh frequencies. The dipolar polarization is vital to develop the permittivity in dielectric materials with permanent dipoles(Figure 3b). Interfacial polarization usually comes into play because the charges between two dielectrics can accumulate at the interfaces,[2,60]especially for the case of dielectric composites(Figure 3b).

To explore the effective dielectric permittivity (ϵeff) of the composites, various mathematical equations have been proposed based on some assumptions, as shown in Table 2. The permittivity of a dielectric composite could be evaluated by one or more of the mathematical equations in Table 2, based on the orientation and geometry of the inorganic filler, volume ratio, the permittivity, and the interaction between the matrix material and filler material. In fact, dielectric loss is always undesirable for the utilization of dielectric materials. In general, there are two types of losses for a real capacitor, that is, the frequency-independent ohmic conduction losses stemming from the long-range charge migration and the frequency dependence of dielectric losses due to the field-related movement of charges associated with the absorption of energy.[70]The loss is mainly caused by electrical conduction and relaxation behavior in a single dielectric material. For a dielectric composite,the mismatch between electrical conductivity and dielectric constant contributes to the charge accumulation at the interface, which produces an additional dielectric loss.[71]Maintaining a low dielectric loss is of great importance for capacitors because loss significantly contributes to Joule heating in capacitor devices.

He Huang is currently a postdoctoral research fellow in the Department of Material Science and Engineering, at the University of Science and Technology Beijing. He received his Ph.D. degree in Mechanical and Aerospace Engineering from the Hong Kong University of Science and Technology in 2019. His current research interests include theoretical studies of the alkali-ion transport mechanism and fundamentals relevant to energy storage materials.

Xinping Mao is a member of China Engineering Academy and a professor at the University of Science and Technology Beijing. His research interest is near net shape manufacturing technology, advanced steel materials, titanium Microalloying Technology, green highperformance automotive steel,etc.

Qiaobao Zhang is currently an Associate Professor in the Department of Materials Science and Engineering, College of Materials, at Xiamen University. He obtained his Ph.D. degree from the City University of Hong Kong in 2016. He joined Prof. Meilin Liu’s group as a visiting Ph.D.student at the Georgia Institute of Technology in 2015.Then he joined Xiamen University in 2016. His current research focuses on the fundamental issues relevant to energy storage systems including Li/Na/K ion batteries, especially on the key electrode materials, interfacial properties and in situ techniques. Till now, he has published more than 110 papers, eighteen of which are highly cited, which attracted more than 6300 citations with an h-index of 42.

3.2. Electrical and Thermal Conductivity

Figure 1. Applications of dielectric composites in various fields.a)–c)Energy storage and energy harvester.a)Reproduced with permission from Ref.[13]Copyright©2017,Elsevier Ltd.b)Reproduced from Ref.[14]Copyright©2015,Royal Society of Chemistry.c)Reproduced from Ref.[18]Copyright©2018,John Wiley&Sons.d)High power application.[28]Copyright©2015,Elsevier Ltd.e)Actuators.[26]Copyright by piezosystem jena GmbH.f)Electrocaloric solid-state cooling devices.[20]Copyright©2015,John Wiley&Sons.g)Electronic circuit.[25]Copyright©2020,American Chemical Society.h)and i)pressure and temperature sensors.[27]Copyright©2015,American Association for the Advancement of Science.Copyright©2015 Tech Xplore.

Electrical conductivity is linked to the movement of carriers, that is,the escape from a localized trap happens when there is feasible activation energy for a carrier to hop over the energy barrier of a trap.As a result, both external electric field and temperature could have a significant influence on electrical conductivity. When a low field is employed to a dielectric, ionic hopping mainly contributes to the electrical conduction, whereas under a high field, the injected electrons are dominant for the conduction of a dielectric. FE polymers demonstrate a low thermal conductivity, whereas FE ceramics and single crystals show better thermal conductivity than FE polymers.[72]The poor thermal conductivity could critically limit the heat conduction in dielectric materials. Therefore, both thermal and electrical conductivity need to be taken into account while designing a dielectric composite.

3.3. Dielectric Nonlinearity

It is well-documented that stored energy density (Ws) of a dielectric system can be defined as follows:[15,16]

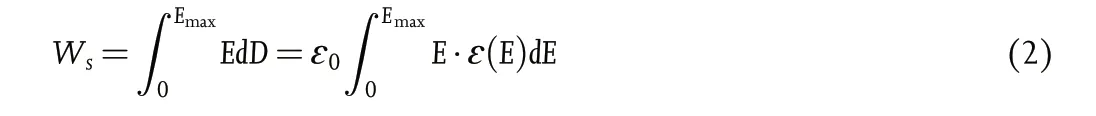
where Emax, D, and ϵ(E) indicate the maximum external electric field, the displacement, and field-dependent dielectric permittivity,respectively. Theoretically, the recoverable or discharged energy density (Wr) and efficiency (η) are given as follows:[16]

Figure 2. Connectivity patterns of the two-phase composite system. The total number of connectivity families is reduced from 16 to 10 due to permutations involved in the composite systems. Reproduced from Ref.[57], Copyright © 1978 Elsevier.

Table 1. Dielectric/piezoelectric/ferroelectric composite development history.

where Dris the remanent displacement and Dmaxis the maximum.Therefore, an energy density loss Wlossis equal to Ws−Wr, which is closely related to the dielectric nonlinearity.

As shown in Figure 4, there is little or no energy loss in linear dielectrics and the energy density of a dielectric system is dominated by the strength of breakdown.Ferroelectric(e.g.,BT)and relaxor FE(e.g.,(1–x)Pb(Mg1/3Nb2/3)O3-xPbTiO3, hereafter referred to as PMN–PT)ceramics possess high permittivities and nonlinear dielectric responses(the paraelectric phase only exists once the temperature is above the Curie point,TC),as shown in Figure 4.[73,74]In most cases,the dielectric permittivity of FEs reduces as the field increases. An AFE material with nearby antiparallel dipoles can develop a large field-induced polarization at a high field.[75,76]The antiparallel dipoles could be constrained along parallel directions once the electric field exceeds the scope of AFE–FE phase switching,leading to a sharp increase in dielectric permittivity during the switching process.[77,78]Such a nonlinear feature is valuable as the electric field-forced phase change could enable a much larger recoverable electrical energy storage capability than linear dielectrics and ferroelectrics. The mechanism of dielectric nonlinearity in a dielectric composite is much more complex than a single-phase material.In recent years,it was reported that the dielectric nonlinearity of composite materials is associated with the conduction of space charges and the relaxation of conduction current.[34,79,80]

Figure 3. Dielectric polarization mechanisms. a) Dielectric response (permittivity and loss) with different frequencies. Reproduced from Ref.[2] with permission from American Chemical Society. b) Schematic of four polarization mechanisms (electronic polarization, ionic polarization, dipolar polarization,and interfacial polarization). Reproduced from Ref.[60] with permission from Elsevier.

For solid-state cooling devices, the electrocaloric (EC) temperature change and entropy change (written as ΔT and ΔS, respectively) can be calculated using the thermodynamic Maxwell relations as follows:[22]

Here, C indicates the specific capacity and ρ represents the material density.The polarizations are determined from the upper branch of the polarization loop,as shown in Figure 4.In the literature,EC strength is

Table 2. Theoretical equations to calculate the effective dielectric permittivity of composites composed of inorganic fillers (ϵ1) and matrix materials (ϵ2).

Table 2. Continued

3.4. Breakdown Strength

Research on the electrical breakdown behavior in dielectric materials goes back to the early last century.[81]To date, mechanisms of shorttime and long-time electrical breakdown have not been fully explained; thus, many apparent challenges exist in the preparation of dielectric composites. In the case of short-time breakdown, it is usually a consequence of several different breakdown effects, that is, electric, thermal, and electromechanical breakdown. The first one is an intrinsic property associated with electron avalanche, which usually happens at low temperatures.[82]When the heat originates from Joule heating and dielectric loss largely exceeds the energy dissipation by conduction and convection, there could be a thermal breakdown. The electromechanical breakdown is caused by the deformation or fracture of the materials, and the breakdown strength (EBD) can be evaluated as follows:[82]

where V represents applied voltage to the material, Y indicates Young’s modulus, and drand doare the reduced and original thicknesses of the sample, respectively.[16,82]In general, the measured electromechanical EBDof a dielectric composite depends on the electrode geometry and contact, voltage frequency, ambient medium, sample thickness, dielectric permittivity, and mechanical mismatches between the matrix and the filler, temperature, and humidity.[16]The long-time breakdown of a dielectric composite under work conditions is related to partial discharges(e.g., internal, surface, and corona discharges).[83]In a heterogeneous dielectric material (for instance, polymer composite),EBDis a combined consequence of various factors, for instance,the geometry of filler, filler/matrix interface, microstructure,defects (e.g., pores), conductivity, and dielectric and mechanical properties.

Figure 4. Dielectric nonlinear and energy storage characteristics of different dielectric materials.Schematic of the electric field versus polarization,P,permittivity,ϵr,and electrostrain,S,of different dielectrics with increased nonlinearity from left to right.The orange area corresponds to the discharged energy.

3.5. Piezoelectric Charge and Voltage Coefficients

The piezoelectric effect is closely associated with the dipole moments,[28,75,84]and the piezoelectric charge coefficient (dij) is expressed as follows:

where D, σ, E, and S refer to the electrical displacement, mechanical stress, applied electric field, and mechanical strain, respectively.The large-signal d∗33can be determined from the unipolar strain performance according to the following formula:

where Smaxand Sminare the maximum strain at maximum field Emaxand the minimum strain, respectively. The field-dependent strain responses of linear dielectrics, paraelectrics, and (anti-)ferroelectrics are schematically displayed in Figure 4. In general, the dijis employed at low frequencies or in nonresonant devices, and the piezoelectric stress coefficient (eij) is used under mechanically clamped conditions or at high frequencies,which can be defined as follows:

The piezoelectric voltage coefficient,gij,is associated with the stressinduced voltage variation,and given as follows:

The piezoelectric clamped voltage coefficient,hij,is defined according to the following equation:

The aforementioned piezoelectric coefficients (dij, eij, gij, and hij) are interrelated as given in the following equations:

where i, j = 1, 2, and 3; k, l = 1, 2, 3, 4, 5, and 6; s indicates the elastic compliance; c is the stiffness; and β is the dielectric impermeability. Note that the transduction coefficient, namely, d33× g33,is among the most important specifications to determine an outstanding performance of piezoelectric energy harvesters, which can be written as follows:[85]

3.6. Mechanical Quality Factor

From a power dissipation point of view,a high mechanical quality factor (Qm) is important in power piezoelectric transducers and resonant applications.[19,75]For a piezoelectric material,mechanical loss(i.e.,the inverse of the Qm) characterizes the power loss over the stored energy,and the Qmis calculated by the following equation:

where fris the resonance frequency and Δf refers to the halfmaximum full width of the resonance peak.[75]It is welldocumented that external conditions could affect the Qmvalues,including contact resistance, frequency, and damping. Other intrinsic factors will also affect Qm, such as domain state, domain size,and polarization rotation angle.

4. Recent Advances in Dielectric Composites for Energy Storage and Conversion

In the past decades, dielectric composites have received evergrowing attention because they show promising potential applications in modern energy storage and conversion systems.[6,7,11,13–19]Dielectric composites can be divided into three categories, namely, polymer–polymer (organic–organic),ceramic–polymer (inorganic–organic), and ceramic–ceramic(inorganic–inorganic) composite materials. Polymer–polymer composites have some unique merits, for example, they exhibit good mechanical properties and are easy to fabricate on a large scale with small dielectric loss, reduced acoustic impedance,and large electrical breakdown strength, although a critical demerit is the low dielectric constant.[2]Ceramic–polymer composite systems are of great interest for designing outperforming properties, which are resulted from the characters of the endmembers, the volume ratio, and the interface property between the ceramics and polymers. In recent years, FE-based ceramic–ceramic composites are promising in high-power and electromechanical applications. To date, the need for highly efficient and environmentally friendly energy storage and conversion is the most important impetus of intensive research activities in dielectric composites. The recent progress in the energy performance of polymer–polymer, ceramic–polymer, and ceramic–ceramic composites are discussed in this section, focusing on the intended energy storage and conversion, such as energy harvesting, capacitive energy storage, solid-state cooling,temperature stability, electromechanical energy interconversion,and high-power applications.

4.1. Polymer–Polymer Composites

The global market demand for piezoelectric devices is estimated to increase from USD 28.9 billion $ in 2020 to 34.7 billion $ by 2025,[86]and the dielectric polymer is undergoing the fastest growth.Dielectric polymers are the preferred materials to fabricate capacitor devices. To date, two widely used dielectric polymers are linear poly(ethylene terephthalate)(PET)dielectric polymer and biaxially oriented polypropylene (BOPP) film, which demonstrates the following measured electrical properties, discharged density of 5 ～ 6 J cm−3, dielectric permittivity of 2 ～ 3, the dielectric loss of 0.0003 ～ 0.002, and EBDof 600 ～ 700 MV m−1.[87,88]As compared with PET and BOPP,PVDF exhibits a higher dielectric permittivity of ～10 with higher breakdown strength. Thus, PVDF or its copolymer has a better energy density as a result of high dielectric permittivity and large EBD. Nevertheless, the PVDF or PVDF-based FE polymers have a deficiency that they can be contaminated by ionic impurities, causing high dielectric losses,in particular at low frequencies and elevated temperatures.[89]

With the rapid advances in modern electrical devices,it is desired to develop polymer dielectrics possessing large dielectric permittivity together with low dielectric loss. To achieve this goal, the polymer–polymer dielectric composite approach has been proposed in recent years.[89,90]In the polymer–polymer dielectric composite films, all polarization mechanisms(electronic polarization and ionic polarization,for instance) could come into play. However, hopping polarization of space charges and FE domain switching in PVDF are disadvantages for applications. Using the multilayer coextrusion process (Figure 5a),Mackey et al.[90]prepared various polymer composites composed of alternating high-permittivity FE polymer layer and high-EBDlinear polymer layer (e.g., polycarbonate (PC)). Phase images for the PVDF–PC 50/50 composites with different layers are shown in Figure 5b.In Figure 5c, there is a relaxation peak in the frequency-dependent dielectric loss of PVDF–PC composite polymers at 75 °C,corresponding to impurity ion-hopping polarization.[90]Moreover,The PVDF–PC and PC–nylon polymer composites show stable energy storage performance up to 125 °C (Figure 5e–g).[91]Past investigations have been focusing on multilayered polymer–polymer composite systems, such as PVDF–PC,[90]poly (vinylidenefluoride–co-hexafluoropropylene) [P(VDFHFP)]-PC,[92]P(VDF-HFP)-poly(methyl methacrylate)(PMMA)-PC,[92]and P(VDF-HFP)-P(VDF-TrFE-CFE).[93]The composite polymer is a useful approach to improve energy storage capacity, especially impeding electrical conduction. Very recently, Yuan et al.[94]reported an allorganic dielectric polymer/molecular semiconductor composite that exhibits a high energy density of 3.0 J∙cm−3and high discharge efficiency of 90%up to 200 °C through the suppression of electrical conduction.The obtained energy storage performance is much higher than that of the existing dielectric polymers and polymeric composites.

Polymeric dielectric composites owing to their flexibility and lightweight have received growing attention in wearable and flexible electronics, energy conversion, and harvesting devices. For example, Ma et al.[95]developed a water-responsive polymer pentaerythritol ethoxylate–polypyrrole composite film actuator, which demonstrated potentials in sensors and power sources for ultralow-power devices.In recent years,polymeric composite-based mechanical energy harvester offers a facile approach for developing flexible devices for ferro- and piezoelectric energy harvesting and storage applications. For instance, Vijayakanth et al.[96]demonstrated that the composites of all organic ferroelectric salts were found to have high output current and power density.Although prolonged efforts in the field of polymer–polymer dielectric composite films have led to much progress in energy storage and conversion,polymer–polymer composites could have a low dielectric loss,enhanced breakdown,and efficiency performance; they do not create much interest because of one common drawback of low dielectric constant.

4.2. Ceramic–Polymer Composites

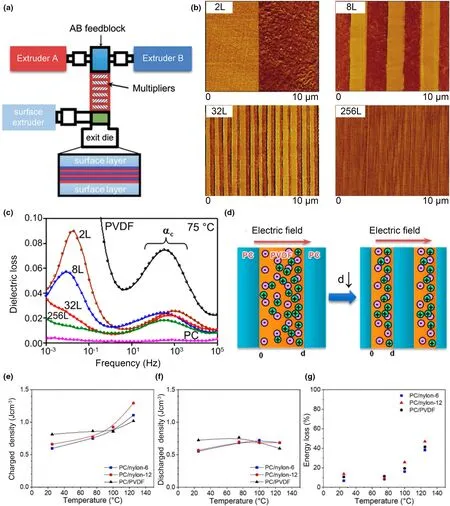
Figure 5. Fabrication of multilayer polymer–polymer composite films. a) Schematic illustration of the coextrusion process of multilayer polymer–polymer films.[89] b) Phase images of PC–PVDF composites with 2-layer (2L), 8-layer (8L), 32-layer (32L), and 256-layer (256L).[90] Dielectric loss and ion-hopping polarization mechanism in the PC–PVDF composite films. c) Dielectric loss for the PC–PVDF composites, PVDF, and PC polymers at 75 °C.[90] d) Schematic showing the ion-hopping polarization mechanism in PC–PVDF dielectric composites.[90] After an electric field is employed, a gradient in charge concentration was induced. Thin PVDF layers have less charge motion and total charge buildup when comparing with thick PVDF layers. Copyright © 2012, American Chemical Society. Energy storage performances. d↓indicates the reduction of the thickness of composite films. e) Charged density, f) discharged density and g) loss of PC-nylon-6, PC-nylon-12, PC-PVDF 33-layer films at different temperatures.[91] Copyright © 2019, American Chemical Society.

FE polymers are flexible, lightweight, and much easier to fabricate at low temperatures as compared with inorganic FE ceramics. It is commonly observed that FE polymers with the incorporation of embedded inorganic nanofillers could have optimized electrical, mechanical, and thermal properties.[15,16]FE polymer nanocomposites have numerous emerging applications, for instance, solid-state coolers, energy harvesting, energy storage capacitors, sensors, and actuators in virtue of their excellent dielectric property and easiness of fabrication.Here,we review recent progress in FE ceramic–polymer nano-/composites targeted for energy storage and energy conversion.

4.2.1. Capacitive Energy Storage

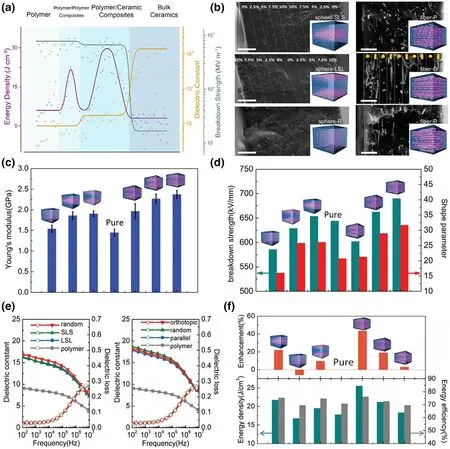
Figure 6. Energy storage performances of polymer–ceramic composites. a) Energy density,dielectric constant, and EBD of dielectric materials in the literature. Reproduced from Ref.[15]Copyright © 2019, Elsevier Ltd. b) Cross-sectional scanning electron microscopy images (Scale bar,2 µm) of BT-P(VDF-HFP) FE nanocomposites. The insets show schematic FE nanocomposites with configurations of sphere-small-large-small composition gradient (sphere-SLS), sphere-reverse large–small–large composition gradient (sphere-LSL), sphere-random (sphere-R), fiber-parallel (fiber-P),fiber-orthotropic (fiber-O), and fiber-random (fiber-R). c) Young’s modulus, d) EBD and shape parameter, e) frequency dependence of permittivity, and f) energy performances of different P(VDF-HFP)-BT composite materials.[113] Copyright © 2018, John Wiley & Sons.

Demands in smaller, lighter, transportable electrical devices and power systems have motivated researchers to develop more advanced materials for high-performance energy storage technologies, e.g., dielectric capacitors,[13–17,97–101]supercapacitors,[102–104]fuel cells,[105,106]and batteries.[105,107]Among them,fuel cells and batteries have high energy storage density,but their low power density and charge/discharge performances limit their applications in power systems. On the contrary,the dielectric capacitors are more attractive for pulsed power systems,electromagnetic guns,and launch platforms, hybrid industrial vehicles,and modern industrial and defense fields due to their high power density, fast charging/discharging rate, and good stability.[2,15,16,108]The discharged density of a dielectric is intrinsically affected by factors such as the dielectric constant and the EBD.For a nonlinear dielectric system,the discharged density is controlled by the efficiency of charge–discharge because there exists energy loss in the processes of energy storage and release. Unfortunately, in pure ceramics or polymers or polymer–polymer composites(see section 4.1),high dielectric permittivity and EBDare hardly achieved concomitantly. In general, dielectric ceramics demonstrate a high dielectric constant but low EBD; meanwhile,the dielectric polymers usually exhibit a low dielectric permittivity but high EBD.Alternatively,combining polymer with ceramic might synergize both advantages and achieve enhanced dielectric properties.

More recently,polymer–ceramic FE nanocomposites are emerging as a promising approach worthy of intensive investigation.Figure 6a summarizes the tendencies of dielectric properties relevant to the energy storage dependent on the components.[15,92,109–112]The permittivity increases and EBDdecreases when increasing ceramic content with polymer and pure ceramics depicting the extreme case scenarios.The energy density, however, shows enhancement for polymer–polymer and polymer–ceramic composites and a lower value for pure polymers and ceramics. Among various composites,the PVDF is utilized in the majority of work,and there is a consensus that the achievement of high energy density requires concurrent improvement of EBD, dielectric constant, and discharge efficiency. By tailoring the interface through organic surfactants, modulating the breakdown path,or suppressing the mobility of free charge carriers,the EBDcan be efficiently improved. Meanwhile,introducing massive ceramic fillers or adding metallic fillers near percolation threshold has been reported to be a reliable solution to improve dielectric constant,however at the expense of decreasing EBDand efficiency. In most cases, energy efficiency is relevant to dielectric loss,that is,high discharge efficiency corresponds to low dielectric loss, which could be achieved by suppressing carrier mobility, tuning the crystalline structure, using polymer nanofillers,instead of ceramic ones,improving the heterogeneity of interfaces, etc. In reality, those parameters need to be taken into consideration as a whole to obtain optimal energy performance. More recently, the modification of the nano-/microstructure in polymer–ceramic composite materials has been proposed to achieve a better energy storage property.For instance,a nonequilibrium processing technique was developed to fabricate several P(VDF-HFP)-BT nanocomposites (see Figure 6b).[113]The addition of BT nanofillers increased Young’s modulus as compared with pure polymer(see Figure 6c).It is clear that the EBDstrongly depends on the configurations (Figure 6d). P(VDF-HFP)-BT composite films demonstrated an improved dielectric constant in contrast to pure polymer, as plotted in Figure 6e. The fiberorthotropic P(VDF-HFP)-BT sample showed the highest discharge density about 25 J cm−3along with an efficiency of about 76%,which improves 45.8%over that of the polymer,as shown in Figure 6f.

4.2.2. Solid-State Cooling

Figure 7. Polymer–ceramic composites for electrothermal energy conversion. a) Electricity consumption in the United States (US) and China (CN).[22] Copyright © 2019, Elsevier Ltd. b) EC cooling cycle of a singlelayer dielectric capacitor. The application of an electric field (E-field) adiabatically polarizes the material with random polarization distribution, leading to the temperature of the material is increased from T1 to T2. Heat is dumped by the relative motion of dipoles along the applied E-field, so that the temperature is reduced to T3 by an isothermal process. Under adiabatic conditions,the removal of the E-field then depolarizes the poled material, and the temperature of the active material is further reduced to T4. Finally, the temperature is increased back to T1 when the heat is absorbed from the regenerator. c) Many publications regarding the ECE per year for the time range from 2000 to February 2021. d) Published papers on ECE in the last 20 years. The data in c) and d) were gathered from the Web of Science, and the keyword “Electrocaloric”was used. The precise number of publications may vary from the data shown here. e) ΔT as a function of EC strength for thin films, polymers, ferroelectric-polymer composites, bulk ceramics/single crystals, and MLCCs. f) The corresponding working temperature at maximum EC temperature change. The solid,horizontal line indicates the room temperature. The open and filled symbols represent the data were calculated by a thermally derived method based on Maxwell relation and measured using direct methods,respectively.

Approximately 20 percent of the world’s total electricity in buildings is used for refrigeration purposes.[114,115]As shown in Figure 7a,25%of electricity in the United States and 20%of that in China were consumed to provide refrigeration and air conditioning. Current vapor compression-based cooling systems are difficult for the sort of miniaturization for coolers.[22,116]Therefore,there is a primary concern for overcoming global warming that we are currently facing by developing environmentally friendly and highly efficient refrigeration technologies.Several non-vapor compression cooling technologies based on thermoelectrics(TE)and caloric effects including the electrocaloric effect(ECE),[117–122]magnetocaloric effect,[123]elastocaloric effect,[124]and barocaloric effect have been developed.[125]TE refrigeration is available in the market;however,the low efficiency limits its further implementation in the major market. The caloric cooling techniques show a potentiality to give a highly efficient cooling solution because the loading and unloading of the external stimuli(electric,magnetic,and mechanical inputs)generate limited hysteresis energy loss.[126,127]Owing to its low cost,direct electricity utilization,and high efficiency,cooling technology based on the electrocaloric(EC)effect(see Figure 7b for the cooling cycle in detail)has quickly regained growing attention since the giant ECE in thin-film PbZr0.95Ti0.05O3was pronounced in 2006 (see Figure 7c).[121]For the improvement of ECE, the FE, AFE, relaxor FE, and paraelectric materials have been studied in various forms, including thin/thick films, bulks, polymers,composites,and multilayers(Figure 7d).

To date, the EC material is dominated by bulk ceramics.Other forms of materials such as composites and multilayers have not yet been fully explored.The amount of composites in EC materials is only 3%,which brings additional opportunities to enhance ECE. Inorganic EC systems in the forms of bulk ceramics and single crystals could achieve high EC strength (ΔT/ΔE); however, the low-breakdown electric field restricts their applications.[128,129]Meanwhile, the issue could be addressed by developing multilayer ceramic capacitors (MLCCs) and thin films, which allow a substrate effect at the same time.[20,130]Nevertheless,the high TCof inorganic EC materials makes it difficult to achieve a high ECE at room temperature. On the contrary, large ECE was achieved at room temperature via a polymer nanocomposite approach,[23,24,131]which survived an ultrahigh electric field.Through modulating the geometry of nanofillers or the boundaries between the matrix and fillers,a high EC temperature change could be realized in polymer nanocomposites. Figure 7e summarizes the EC temperature change as a function of EC strength of ceramics,single crystals,thin films,MLCCs, and polymer nanocomposites. Data were collected from the literature.[20–24,106,132–150]Notably,the polymer nanocomposites usually have a smaller EC strength than inorganic bulks and thin films, but they provide a large EC temperature change near room temperature compared with other material systems (Figure 7f). The detailed EC performances of different material systems are also summarized in Table 3. With the rapid development of fabrication methods, some drawbacks of EC materials in different forms arebeing addressed. For instance, high EC strength (ΔT/ΔE) was recently reported in the all-scale hierarchical structures of P(VDF-TrFE-CFE)-based FE nanocomposite materials with fillers of BiFeO3nano-sized particles in Ba(Zr0.21Ti0.79)O3nanofibers.[23]In the near future, several critical factors such as the structure of the nanocomposites, material combinations, and device integration need to be taken into account to accomplish the development of high-performance EC cooling systems.In addition, domain engineering and interfacial engineering may provide opportunities to achieve high EC performance of ferroelectric ceramic–polymer nanocomposites.

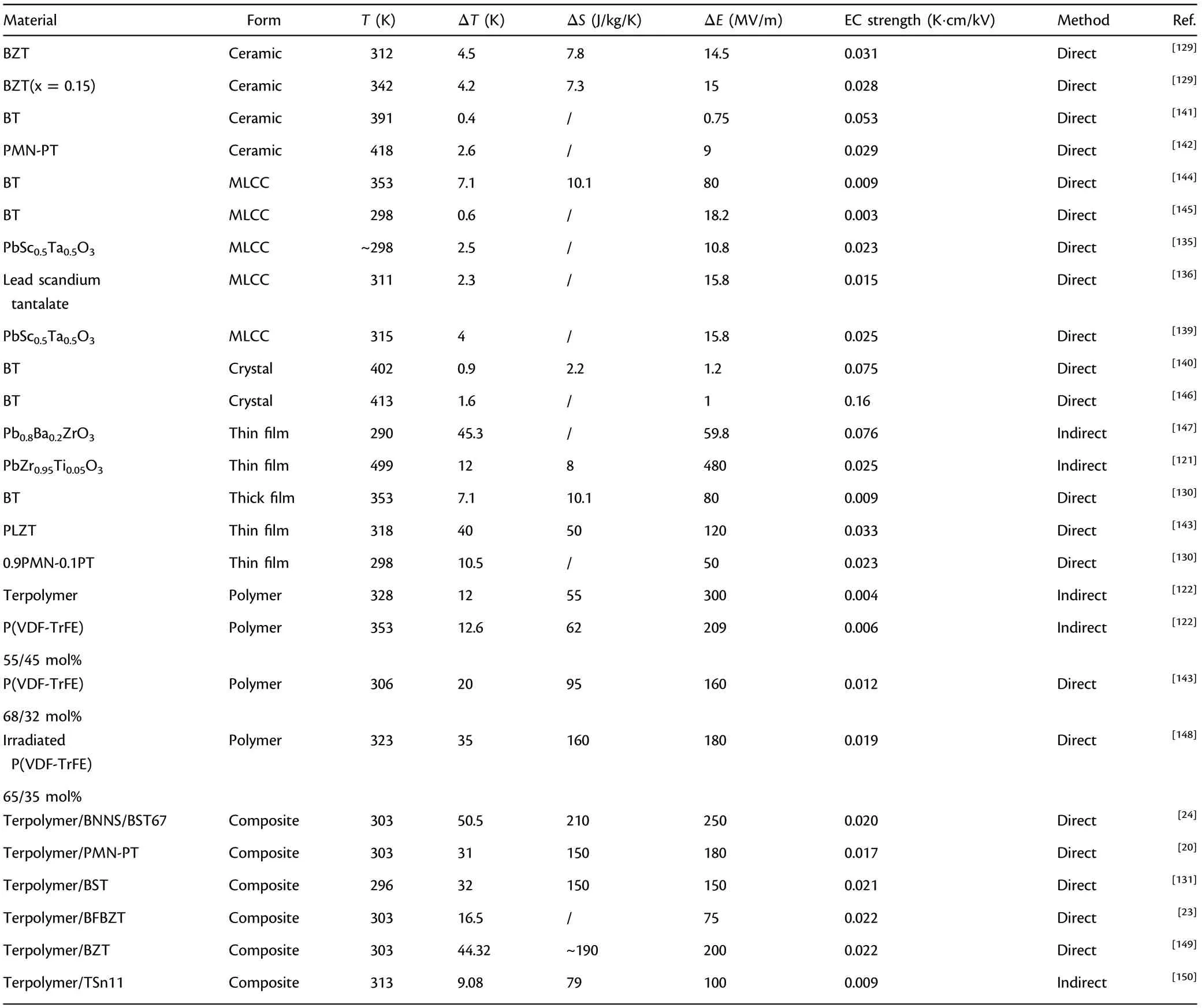
Table 3. Summary of the ECE among different material systems.

4.2.3. Sensor and Actuator

PZT as a piezoceramic was documented in the 1950s;since then,it has been extensively applied for actuators and sensors.[150,151]However,these single-phase piezoelectric ceramics have poor mechanical ductility and fragile cracks, which limit their application in integrated selfpowered sensors.[152,153]Moreover, the problems of piezoelectric ceramics in impedance matching and mechanical properties compatibility limit their application in the malleability field as monitoring sensors.Fortunately, polymer-based composites extend the diversity of design freedom,which enables their possibility to meet the need of the aforementioned applications. By taking full advantage of the inorganic ceramic filler and the organic polymeric matrix, ceramic–polymer composites are candidates for self-powered sensor applications. As a result,all types of ceramic–polymer composite-based sensors have been under exploration with great attraction, including PZT, BT nanofibers,and nanoparticles in combination with PVDF,[154,155]PVDF–TrFE,[156,157]polydimethylsiloxane (PDMS) nanowires,[158]and so on.Such ceramic–polymer composites exhibit good mechanical flexibility and structure reversibility. However, when the sizes are reduced to nano-or microscale for highly integrated electronic circuits,the dielectric constants of these composites are usually not as good as their bulk counterparts, leading to poor piezoelectric response with low d33and g33. Most recently, Gao et al.[159]fabricated a PDMS-based piezocomposite touch sensor (Figure 8a) and wearable keyboard (Figure 8b,c),and the device exhibited an excellent sensitivity(Figure 8d),which is very promising for high-performance flexible devices. Park et al.[27]designed a sensor, and the reduced graphene oxide (rGO)-PVDF composite was sandwiched between Au electrodes (Figure 8e).They demonstrated that the rGO-PVDF FE nanocomposite film can detect and discriminate multiple stimuli such as pressure (Figure 8f),vibration, and temperature (Figure 8g) with high sensitivities. In the future, the pursuit of overall high-performance composites, including interface compatibility, mechanical ductility, and the high response of multifunctionality, will be a hot research topic for ceramic–polymer composites for next-generation smart sensors.

4.2.4. Energy Harvesting

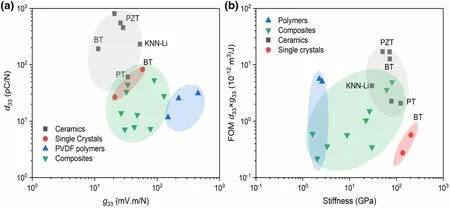
Figure 9. Polymer–ceramic composites for piezoelectric energy harvesting. a) d33 vs g33 and b)energy harvesting figure of merit, d33 × g33), versus Young’s modulus or stiffness in the thickness direction for different piezoelectric materials. The data were collected from Ref.[72,85–93,160,161]

In recent years, piezoelectric energy harvesting technologies have attracted growing interest for applications in flexible and wearable electronic devices, sensing, and monitoring networks.[17,160–164]Because various vibrations are ubiquitous in the environment, a piezoelectric energy harvester has become a promising candidate for resolving the environmental problems that we are currently facing due to the consumption of fossil fuel energy. The piezoelectric ceramic filler particles in the uncured 0-3 ceramic–polymer composites can align in chain-like structures.As a result,the 0-3 composites can exhibit a large g33at low volume fractions of fillers.[159,165]In this case,the stiffness and ductility of the matrix polymer dominate, and the composites remain flexible.The d33versus the g33, and the energy harvesting figure of merit(d33× g33) versus Young’s modulus (Y) for different piezoelectric systems are shown in Figure 9a,b. Piezoelectric ceramics and single crystals have excellent d33,[51,74]neverthess,their high stiffness makes it very difficult to directly assemble them into flexible and wearable electronics with require structures. Even though the PVDF polymer has a g33of about 200 mV m N−1, the low TC(e.g., P(VDF-TrFE) (65/35)has a TCof 100 °C) severely limits its operational temperature window.[166]The TCof ceramic–polymer piezoelectric composites remains that of the ceramic filler in first-order approximation, but the main shortcoming is that the g33lags behind that of polymers such as PVDF.The search continues for ceramic–polymer composites with an adequate figure of merit (FOM) and low stiffness for piezoelectric energy harvesting. However, the state-of-the-art ceramic-polymer piezoelectric nanocomposites are facing a major challenge of enhancing one property(e.g.,d33)at the cost of the other(e.g.,g33).P(VDF-TrFE)copolymers exhibit behaviors reminiscent of a morphotropic phase boundary that is widely used to design high-performance inorganic piezoelectrics,and a d33of −63.5 pC N−1has been realized in morphotropic phase boundary P(VDF-TrFE) copolymers.[167]This may provide a way to prepare a polymer matrix with a high piezoelectric charge coefficient.Attempts have not yet been made to fabricate composites based on morphotropic phase boundary P(VDF–TrFE)copolymers and ceramic fillers.Recently,research interests are directed to develop flexible and lead-free piezoelectric composites due to the toxicity of Pb,[168]and lead-free piezoelectric composites have promising applications in tire pressuremonitoring systems,[169]structural health monitoring,[170]and energy harvesting.[17,164]Therefore, ceramic–polymer Pb-free piezoelectric composites would be one of the hot topics in the next few years.

4.3. Ceramic–Ceramic Composites

Comparing with dielectric polymer and polymer-based composites,ceramic–ceramic composites lack flexibility and have low breakdown strength. This is the main reason why the energy performance of ceramic–ceramic dielectric composites has reached a plateau over the past years. Development in ceramic–ceramic dielectric composites with polar orders is largely due to the progress in lead-free piezoceramics and the improvement in the microstructure of basic ceramics.Over the last 20 years,prolonged efforts have led to certain progress in developing lead-free piezoceramics.[11,19,66,168,171,172]Several lead-free candidates have been reported so far including BT, K1/2Na1/2NbO3(KNN),and Na1/2Bi1/2TiO3(NBT)-based materials.[168,171,172]Although the lead-free alternatives cannot replace the PZT family of materials in all applications, certain niche areas like high-power ultrasonics have been identified where KNN-and NBT-based materials demonstrate advantages over PZT.[19,66,168]Nevertheless, leadfree piezoceramics find limited applications due to their pronounced drawback concerning the poor thermal stability of the piezoelectric and ferroelectric properties. For example, d33significantly decreased at the depolarization temperature (Td～100 °C) of the (1–x)(Na1/2Bi1/2)TiO3-xBaTiO3(hereafter, simply NBT-xBT) composition.[168]A ceramic–ceramic composite strategy was proposed to tune the microstructures of these materials,contributing to a better thermal stability. Early studies on Pb-free piezoceramics focused on 0-3 type ceramic–ceramic composites,[57]where the randomly distributed FE “seeds” embedded in an ergodic relaxor FE matrix.[64,65]

More recently, the ceramic–ceramic composite is a powerful approach to tailor electrical properties of ferro-/piezo-/dielectrics. For instance, NBT-6BT (matrix) and ZnO (NBT-6BT/ZnO) composites exhibit higher Td[11]and a large increase in Qmwhen compared with pure NBT-6BT.[19]This may open up avenues in the search for suitable oxide inclusions[173]to tailor relaxor/ferroelectric stability[174]and materials with high Qm.However,the brittle nature and high density of FE composite ceramics, of course, limit their proposed applications in flexible electronics.Previous studies mainly focused on the thermal stability and electromechanical energy conversion performance of bulk FE composite ceramics. Therefore, we summarize the recent advances in ceramic–ceramic composites targeted for energy electromechanical energy interconversion and high-power applications.

4.3.1. High-Power Applications

For high-power applications such as ultrasonic cleaners,ultrasonic nebulization devices,piezoelectric voltage transformers,and hard piezoelectric materials with good thermal stability are highly demanded.[166]Recently, several approaches have been proposed to achieve hardening effects in piezoceramics,[11,19,66,171,172,174,175]for example, chemical dopants in combination with corresponding defects (vacancies and lattice defects), grain boundary-related two-dimensional hardening and composite-based three-dimensional hardening. The point defects or inclusions could pin the domain walls, constrain their mobility, and result in “hard-type” ferroelectrics. However, the increase in thermal stability directly causes reduced piezoelectric properties, and most improvements of the piezoelectric properties are at the cost of thermal stability. To mitigate the incompatibility between thermal depolarization and large piezoresponse, most recently, the increment of depolarization temperature up to 125 °C and retained d33as high as 80 pC N−1have been achieved in the relaxor–semiconductor (NBT-6BT/ZnO)composites with designed microstructures,[11]as established from an ex situ study tracking the retained d33(Figure 10a,b).The reason for hardening was initially ascribed to the partial depolarization field compensation via the free electrons of ZnO.Later,the depolarization behavior tracked in situ for different contents of ZnO (Figure 10c)established the operational temperature limit as 140 °C. The residual stress resulted from the different thermal expansion mismatch between the NBT-6BT and the ZnO[171,174]was proposed to stabilize an FE order, thus increasing the depolarization temperature (Figure 10c).Despite the enhancement of depolarization temperature, the relaxor–semiconductor composite approach is an effective way to achieve a two-fold enhancement in Qmas compared with pure NBT-6BT,[19]as displayed in Figure 10d.The enhancement of Tdand Qmwill provide a new solution for a high-power system of Pb-free piezoceramics.

Figure 10. Ceramic–ceramic ferroelectric composites for high power applications. a) The microstructure and b) retained d33 of 0-3-type NBT-6BT:0.3ZnO composite.[11] Copyright © 2015,Macmillan Publishers. c) d33 vs temperature for NBT-6BT:xZnO composites.[171] Copyright © 2017,Elsevier Ltd.d)Qm of poled NBT-6BT:xZnO samples.[19]Copyright©2017,American Institute of Physics.

4.3.2. Electromechanical Energy Conversion Devices

Artificial intelligence is now offering abundant opportunities for high-performance electromechanical devices.[176,177]As shown in Figure 4, dielectric materials such as FEs, relaxor FEs, and AFEs with multiple strain responses are arousing intensive research interest.[178–180]Among them, hard PZT and relaxor FE ceramics are dominant in the market.[181]For most applications, high strain, low hysteresis in strain response, and high thermal stability are always desired for electromechanical applications.[73]For example, the working temperatures of the electric compressors and sensors used in gas exploration are ranging from 170 to 300 °C.[182]However, the widely used hard PZT exhibits a very large hysteresis (>50%, see Figure 11a),and the use of the toxicity of lead also poses strong threats to serious environmental concerns, driving the prolonged search for leadfree candidates.[182]As one example, the actively investigated leadfree NBT-based materials exhibit an electrostrain value of 0.3 ～ 0.7%accompanied by a very large hysteresis (>35%),[183]as shown in Figure 11a. To mitigate the incompatibility between small hysteresis and large strain, the strategy of forming ergodic–nonergodic(or REFE)composites was reported to be efficient by introducing a relaxor phase into an FE matrix,[66,184,185]for example, the Na1/2Bi1/2TiO3–BaTiO3–K1/2Na1/2NbO3(NBT-BT-KNN) RE-FE composite exhibiting an induced strain of 0.12 ～ 0.15% and a strain hysteresis of 20 ～ 35%.[184]Chemical modifiers,optimized compositions(e.g.,morphotropic phase boundary composition), and the configurable design of ceramic-based composites may be important for simultaneously obtaining large field-induced strain and low hysteresis in strain response. Therefore, the selected composition should have a high strain, and the FE ordering can be easily developed by applying an external field. For instance, a high strain of 0.72% along with a strain hysteresis of 36.2%was recently reported in modified NBT-based ceramics.[186]The giant strain stemmed from the reversible change between the FE state and the ergodic one under an external electric field. Recently, a high strain of ～0.51% accompanied with a hysteresis of about 29% and excellent stability were simultaneously achieved in oriented NaNbO3-doped NBT-6BT ceramics.[187]Although promising developments are made in NBT-based RE–FE composite ceramics, these materials still face a problem of increased hysteresis upon cooling(Figure 11b,c).The hysteresis increase at low temperatures is related to intrinsically cooling-driven transition from the RE-to-FE state,which also explains the temperature-sensitive hysteresis of the PMN and NBT-based ceramic materials,[188,189]as displayed in Figure 11c. To solve this critical issue of intrinsic incompatibility between broad temperature window and low hysteresis, a re-entrant RE–FE composite (RRFC)(Ba0.925Bi0.05)(Ti1−x/100Snx/100)O3(later, simply BT-5Bi-xSn) system was reported by introducing a sufficient disorder to develop a re-entrant relaxor state.[184]With the help of the creation of local polar nanoregions,the re-entrant transformation allows additional electromechanical degrees of freedom and also prefers the RE state,rather than the FE state during cooling. As a result, low hysteresis smaller than 20% and large electrostrain higher than 0.1% in a temperature window up to 168 °C have been realized in the RRFC composite ceramics.[184]

Despite the aforementioned methods, the design of RE-FE composites is an effective way to achieve large electromechanical responses with practically viable thermal and cyclic stability. Figure 11d shows the large-signal piezoelectric coefficients of the representative lead-free piezoceramics at room temperature.[168,172,186,189,190]BT-based, e.g.,Ba(Zr, Ti)O3-(Ba, Ca)TiO3(BZCT), lead-free materials usually demonstrate poor temperature stability (low TCor frozen temperature Tf),whereas KNN-based piezoceramics exhibit relatively small strain and d33, which would limit their applications in smart actuators and highperformance electromechanical devices.The NBT-based incipient piezoceramics show great potentiality,but the relatively high field is needed to trigger the giant strain; meanwhile, the large hysteresis also hinders their applications. Thus, the RE–FE composite has been considered as a sufficient approach to overcome the disadvantages stated before. The RE–FE composites already show large piezoelectric coefficients, which are comparable with that of the commercialized PZT ceramics (Figure 11d).It should be noted that,however,RE–FE composites still have lower TC(or Tf) than that of the PZT family. Many efforts need to be made to increase the temperature stability and optimizing the density and flexibility of RE–FE composites. Here, we plot the measured d33over the mass density and the elastic compliance against selected piezoelectric materials,[191–199]as shown in Figure 11e. The piezoelectric composites could have a larger specific piezoelectric constant(i.e.,|d33|/ρ) and higher elastic compliance than hard and soft PZT ceramics. The low-density and flexible piezoelectric composites suggest a promising application as a simultaneously highly sensitive and lightweight smart actuator and sensor.

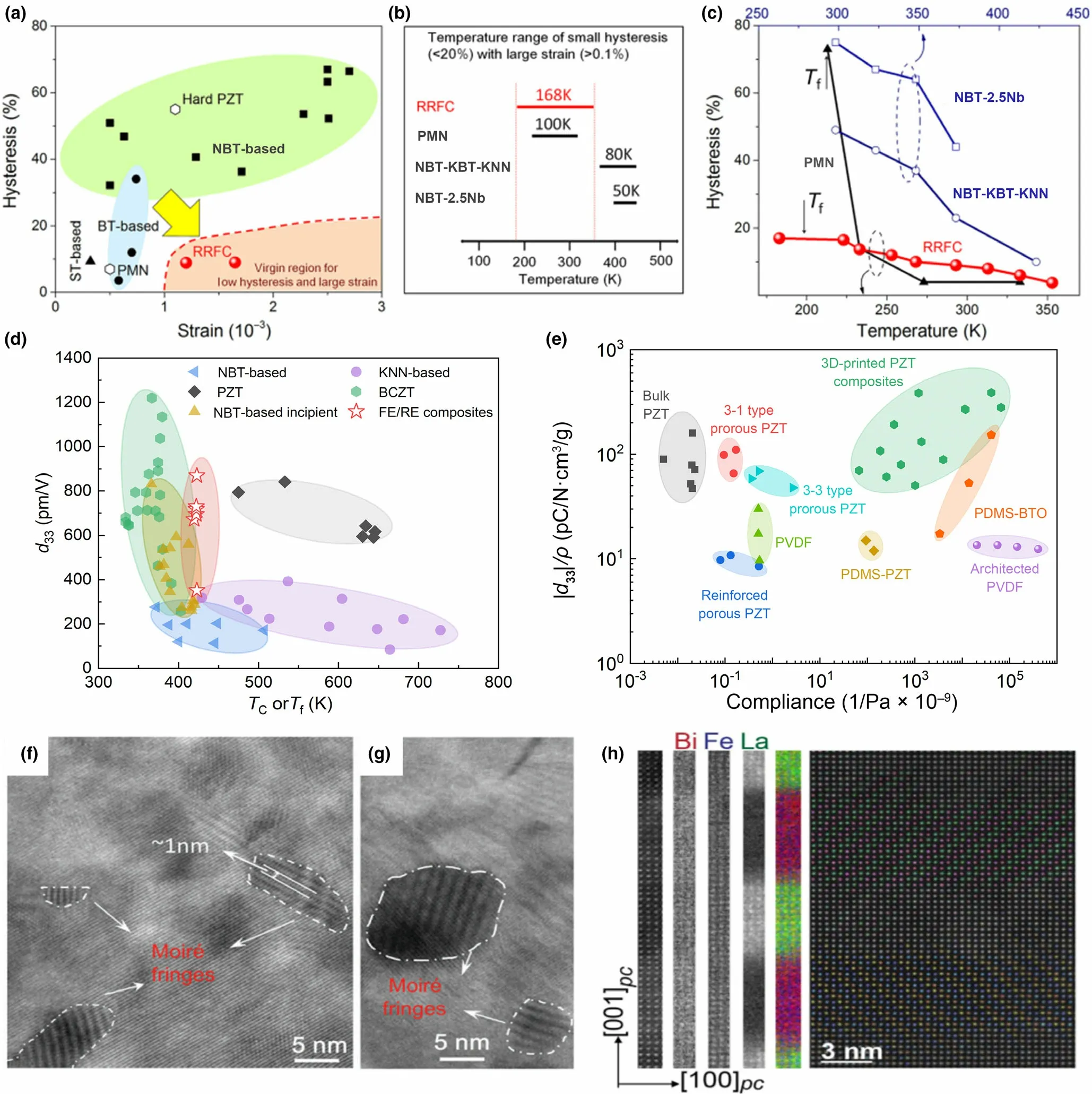
Figure 11. Ceramic–ceramic ferroelectric composites for electromechanical energy conversion. a) Room temperature hysteresis and the maximum strain among the RRFC composite, hard PZT, PMN, and other Pb-free systems including NBT-based, SrTiO3(ST)-based), and BT-based.[184] b) Temperature window for the RRFC composite, PMN, and two representative NBT-based ceramics, NBT-2.5Nb and NBT-KBT-KNN. c) Hysteresis vs temperature for various system RRFC, PMN, NBT-2.5Nb, and NBT-KBT-KNN. The Tf indicates the freezing temperature. a–c) Copyright © 2018, Springer Nature. d) d33 vs temperature for KNN-based, BCZT, NBT-based piezoelectrics, PZT, and FE-RE composites. Data are collected from Refs.[168,172,186,191] e) Specific piezoelectric charge coefficients vs elastic compliance for various piezoelectric materials. Data are collected from Refs.[192–199] f–g) TEM images showing Moir´e fringes and the existence of PNRS.[203] Copyright © 2018, The Royal Society of Chemistry. h) Atomic concentrations of bismuth, iron, and lanthanum in red, blue, and green, respectively.Two different atomic-scale deformations of the BFO layer are observed as twin variants as viewed along the [010]pc. Reproduced from Ref.[205] Copyright ©2018, arXiv.

Recently, a route was proposed to enhance the piezoelectric charge/strain coefficients and power density by texturing the (Ba,Ca)(Ti, Sn)O3-BT dielectric composites.[200]It is noteworthy that high piezoelectricity is not the fixed criteria for obtaining a good overall performance when referring to the RE–FE composite design,For instance, the design space of piezoelectric coefficients, the corresponding reliability, and flexibility are highly desirable to extend the promise of RE–FE composites. In addition, the introduction of proper local structural heterogeneity (LSH) was proposed to enhance piezoelectric response and polarization, and the complex polar states such as PNRs are addressed to induce LSH in relaxor ferroelectrics.[201,202]PNRs can contribute to the high piezoelectricity and excellent stability, resulting from the structural homogeneity induced FE-to-relaxor transition.[203]High-resolution transmission electron microscopy results (see Figure 11f,g) demonstrate that the Moir´e fringes indicate the evidence of PNRs, which belong to one of the induced LSHs.[203]For nanoscale structural heterogeneity in composite materials, effective techniques were developed to manipulate the interfaces, such as solvothermal or hydrothermal method,[204]and molecular beam epitaxy method for the fabrication of superlattices. As one example, Figure 11h shows the Pnma AFE phase of BiFeO3(BFO) in (La0.4Bi0.6FeO3)n/(BFO)nsuperlattices.[205]

The composite approach has also been used to realize hightemperature capacitors with stable permittivity in a wide temperature window. Although chemical modifications and ternary solid solutions have been utilized to develop new compositions,[206,207]the key demand for capacitors working at high temperatures is also lower thermal conductivity. In this regard, the composites of BaTiO3with ZnO inclusions utilize the residual stress approach to enable a multiphase coexistence, thus widening the temperature window ranging from 100 to 176 °C, with ±15% change in permittivity and lower dielectric loss smaller than 0.02. In ferroelectric systems, the composite approach can be used to suppress the phase transition and flatten permittivity, but this also comes at the cost of reduced permittivity(due to lower permittivity of the oxide inclusions). This then opens up the avenues for developing new composites with suitable oxide inclusions to achieve a high and stable permittivity in a wide operational temperature range.

4.4. Other Composites

Composite materials containing ferroic orders such as ferroelectric–ferromagnetic and ferroelectric–multiferroic composite systems are provoking much research activity due to their profound physics and potential applications in sensors, memories, and spintronics.[208–211]However, these composites are out of the scope of this review, and the progress in these composites has been summarized in the recent reviews.[208–210]One has to note that ferroelectric composite materials have shown great potentiality for many other new applications such as ferroelectric memory devices,[212,213]flexo-photovoltages,[213]and advanced nano-/micro-electromechanical systems based on flexoelectric composites.[214,215]In addition, the ferroelectric nanocomposite may be a good platform for exploring nontrivial topology in ferroelectrics.[8]For example, the polar skyrmion was demonstrated in a ferroelectric nanocomposite consisting of a cylindrical BT nanowire embedded in a nonpolar SrTiO3matrix.[8]Ferroelectric-based composite materials are particularly appealing not only because they hold the properties of the parent compounds but also because they offer additional design parameters based on the matrix and the filler,leading to new structures and functionalities.

5. Emerging Fabrication Techniques for Dielectric Composites

Dielectric composites show fascinating performances such as higher temperature stability,higher dielectric permittivity,higher energy storage capability,and larger electrocaloric temperature change.The electrical and mechanical properties mainly benefit from the configuration of fillers in the dielectric composites. Consequently, it is of great importance to developing fabrication methods that can manipulate the architecture of fillers in a matrix and design the microstructure. In recent years, new emergent approaches have been proposed to prepare composite dielectrics, including 3D printing,[195]electrospinning,[216]and cold sintering.[217]In the following text, we briefly describe the fabrication techniques of dielectric–ferroelectric composites.

5.1. 3D Printing

Additive manufacturing (e.g., 3D printing) allows the high fidelity printing of millimeter- to centimeter-scale objects with complex 3D architectures,making it a straightforward,yet versatile,fabrication technique for both science and industry.The progressive alignment of fillers during the 3D printing process is schematically illustrated in Figure 12a. Recently, ceramic–polymer composites have been printed using 3D printing, which may be exploited to fabricate devices that require materials with high permittivity.[192,195,218–220]Castles et al.[220]demonstrated that 3D-printed BT–acrylonitrile butadiene styrene composites(see Figure 12b,c)exhibited enhanced real part of dielectric permittivities, which were reproducible over the entire manufacturing process.Moreover,the dielectric permittivity can be modified by changing the dimensional patterning in a 3D printing process. Cui et al.[192]reported that 3D-printed electromechanical architectures showed high specific piezoelectric coefficients and tailorable flexibility. 3D printing can be extended to piezoelectric ceramics(e.g.,PZT and BT)and multifunctional composites. 3D printing of dielectric composites, especially polymer–ceramic composites,have already developed at a rapid pace in recent years.However,several common drawbacks of 3D printing need to be overcome before it is widely used by most industries. First, the wide application of this technology is strongly restricted by printable materials.Currently,only a few polymers and powders have been used in the 3D printing process.[219]Therefore,there is a critical need for the discovery of new reinforcement and synthesis of matrix materials which could be used to improve the versatility of composites printing.Second,the printed composites usually show low mechanical strength and low electromechanical breakdown strength.This is the reason why the electrical performance of 3D-printed composites is rarely documented in the literature.Last but not least,it is difficult to manufacture composites that have large volumes because most of the current 3D printing processes are time-consuming. Consequently, new printing approaches with fast and scalable processing of materials need to be developed.[221–223]Researchers are now exploring new materials focusing on processing control, scalability, and mechanical and electrical performances of 3D-printed products, and novel applications of 3D manufactured composites.

5.2. Electrospinning

Electrospinning is an attractive one-step technique for preparing uniform polymeric micro-/nanofibers and their composites at long length scales and in a continuous process, making full advantages of constituents.[216,224]To date, multiple structures and morphologies of polymers, ceramics, metals, metal oxides, and inorganic–inorganic,organic–inorganic, and organic–organic composites have been fabricated using the electrospinning method.[224]For example, the polyimide (PI)/multi-walled carbon nanotubes (MWCNTs) nanocomposites were prepared, which demonstrated good mechanical flexibility,[225]high relative dielectric constant of 217, and the five-fold increase in energy density using electrospinning.Liu et al.[226]fabricated polysulfone-MWCNT composite dielectrics with improved permittivity,low loss, and high energy performance. Overall, electrospinning may be a useful technique to fabricate nanocomposites for energy storage and conversion. Despite these achievements, common shortcomings still exist.For example,aligning or dispersing the nanofillers in a polymeric matrix is still one of the most challenging aspects of preparing ceramic–polymer nanocomposites. In addition, pores or voids may be unavoidably introduced into the nanocomposites, which leads to a decrease in EBD.[16]As a result,there is in desperate need for proper dispersion of nanofillers, and several strategies have been addresses to improve the dispersion of nanofillers, including the drying process,subsequent heating treatment,and chemical modification of nanofillers.As one example,the nonequilibrium method was recently developed to achieve a homogeneous distribution of inorganic nanoparticles in BT-P(VDF-HFP) FE polymer composites.[20,227]This method could be extended to other nanocomposites such as a nanocomposite with parallel BT nanofibers(Figure 12d).

5.3. Cold Sintering

Sintering is very important in the processing of metals, metal oxides, ceramics, and polymers into a dense solid.[228]In principle, the co-sintering of ceramic and polymer into a solid with high density is impossible due to the large different processing temperature gaps of ceramic and polymer, as shown in Figure 12e. Recently, cold sintering, known as a low-temperature sintering process, has been proposed for ceramics and composites.[217,229]For example,CaCO3,[230]ZnO,[231]and Na0.5Bi0.5MoO4-Li2MoO4have been prepared by using a cold sintering or electric field-assisted cold sintering process.[232]In the next few years, there are many opportunities and possibilities to redesign ceramic–polymer composites based on cold sintering techniques, as schematically shown in Figure 12f,g.Many factors can influence the dielectric breakdown strength, such as the electromechanical breakdown model, electron avalanche, and thermal runaway. Generally, the dielectric EBDof bulk ceramics is much smaller than that of polymers, and thus, the EBDof ceramics will be increased by designing ceramic–polymer composites. For example, the obtained EBDof cold-sintered Na2Mo2O7–polyetherimide (PEI) composite ceramics with 10 ～ 20 vol% of PEI was enhanced from ～55 to ～107 MV m−1.[233]Although the understanding of the transdisciplinary cold sintering method is ongoing,we anticipate that the cold sintering method could open up avenues for preparing polymer-based composites with high EBDand also could contribute to future developments for composite-based multifunctional electronic devices.

5.4. Other Methods

Many other fabrication approaches have been utilized to prepare FEbased composite materials,[16,234]including traditional mechanical rolling,[10]ball milling,[235]freeze casting,[236]dielectrophoretic,[237]strain assembly,[238]and template-assisted fabrication.[239]It was reported that mechanical rolling enables the alignment of TiO2/MWCNTs in the PVDF matrix, contributing to enhanced EBDand suppressed dielectric loss.[10]Ball milling has been widely employed to reduce the particle size of inorganic ceramics,and it has been extended to align ceramic filler in certain polymers.[235]Recently,the freeze casting process has been employed to produce FE-based composite materials with desirable dielectric properties.[236]For instance, Kim et al.[236]used the freeze casting strategy to align BaTiO3nanoparticles in epoxy composites, resulting in a two-fold enhancement of permittivity as compared with the composites with the randomly mixed composites.Dielectrophoretic assembly is a new route to prepare anisotropic polymer-based composites.[237]The dielectrophoretic assembly allows the fabrication of nanocomposite systems with well-ordered fillers,but it is limited to producing composites with aligned fillers at low concentrations. Therefore, the strain assembly method has been considered as a sufficient way to align fillers in nanocomposite materials with a high filler concentration.[238]To prepare dielectric nanocomposites with a well-aligned structure,a template-assisted fabrication approach has been recently used to prepare nanoporous anodic aluminum oxide–PVDF composites with relaxation and relaxor–ferroelectric-like response.[239]However, proper fillers and polymers are needed to be used as templates to produce different FE polymer nanocomposites with controlled structures.

Despite remarkable achievements in fabricating dielectric composites,each approach has its drawback. For instance, voids or pores may be unavoidably induced into the polymer-based nanocomposites during the electrospinning process, resulting in a decrease in energy density and EBD. Most of the 3D-printed dielectric composites cannot meet the requirements of the functional properties and large-scale production.A growing number of ceramics can be readily sintered using cold sintering, which may open up new multi-material space for fabricating unique ceramic–polymer composites.Note that the cold sintering is yet new,and it has not been applied to manufacture ceramic–ceramic composites like relaxor–ferroelectric and AFE–FE composites. In fact, fabricating composites is only at the primary stage,and plenty of efforts on fabrication techniques should be developed in the future.

6. Challenges and Future Opportunities

Ceramic–polymer nano-/composite dielectrics are candidates for piezoelectric energy harvesting, capacitors, high-efficiency solid-state refrigeration, and sensors. As compared with BOPP polymers, the dielectric loss needs to be further reduced to obtain a long lifetime. Therefore,the concurrent improvement in the EBD, permittivity, and piezoelectric and electrocaloric performances of ceramic–polymer composite materials has been pursued to achieve more practical applications.RE–FE composites have shown enhanced thermal depolarization temperature,improved mechanical quality factor, and high-performance electromechanical properties. Despite the certain progress, the lack of simultaneously high piezoelectric response and insensitive temperature stability restricts the real applications of RE-FE composites.To improve the temperature stability and piezoelectric response,approaches were proposed to modify the microstructure and interfaces, such as domain engineering and structural heterogeneity via chemical routes.[200,240]Here, we highlight the challenges and future opportunities for developing highperformance dielectric composites.

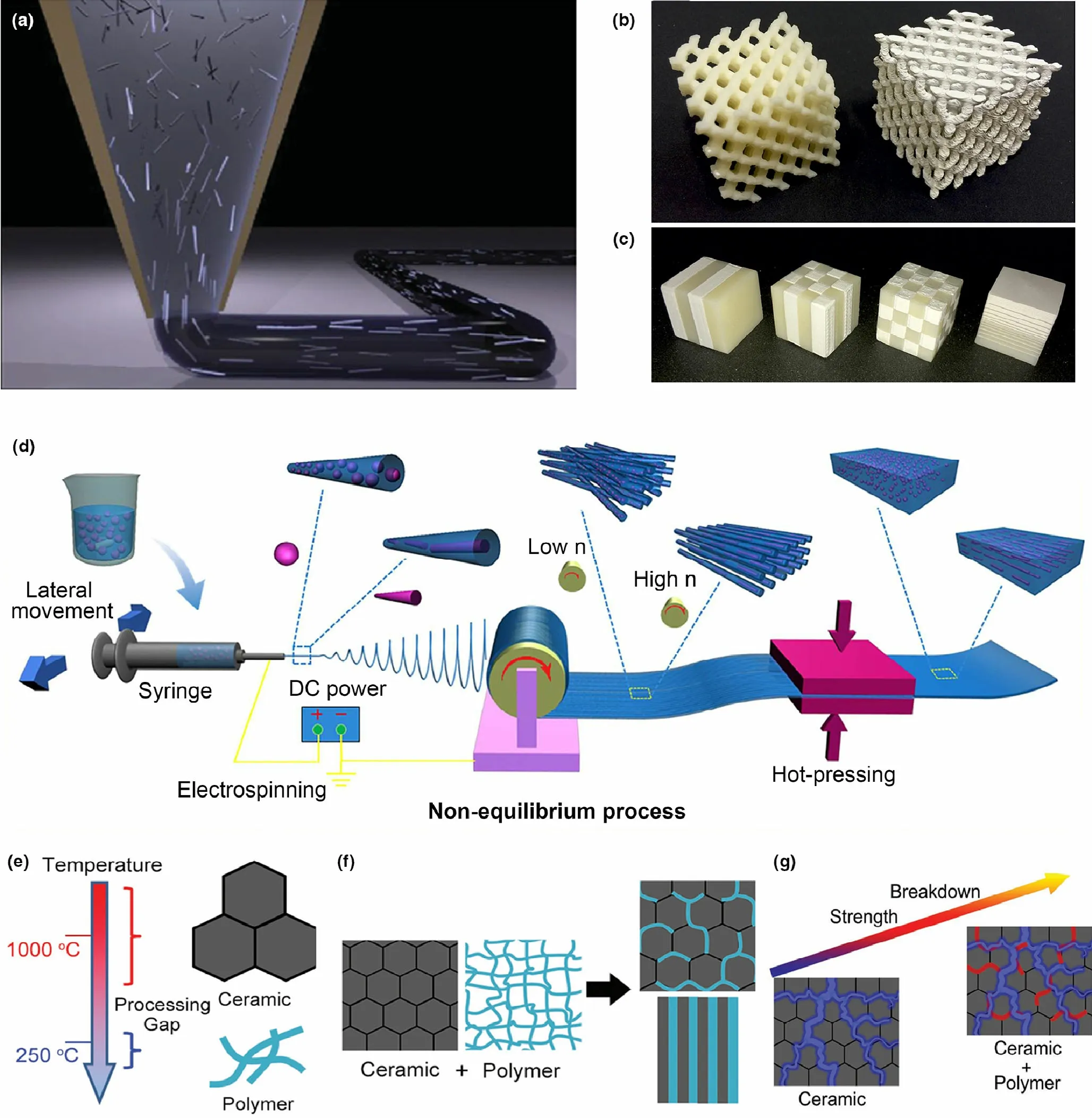
Figure 12. Emergent fabrication techniques of dielectric composite materials. a) Schematic showing the 3D printing system with the progressive alignment of fillers during composite ink deposition.[218] Copyright © 2014, John Wiley & Sons. b) 3D-printed acrylonitrile butadiene styrene polymer (left) and 50 wt% BT acrylonitrile butadiene styrene polymer composite (right). In Figure b), each 3D-printed structure has a side scale length of 32 mm. c) 3D-printed 1D, 2D,and 3D periodic composites as well as a 1D graded structure using 50 wt% BT and acrylonitrile butadiene styrene polymer. Each 3D-printed structure has a side scale length of 16 mm.[220] Copyright © 2016, Springer Nature. d) Schematic showing the non-equilibrium method.[227] Copyright © 2018, John Wiley &Sons. e, f) Schematic showing the processing temperatures of polymers and ceramics, and g) ceramic-polymer composites. Reproduced from Ref.[229]Copyright © 2018, John Wiley & Sons.

6.1. Domain Engineering and Structural Heterogeneity Design

Ultrahigh d33over 2100 pC N−1was reported in successfully domainengineered PMN–PT single crystals through the reduction of 71°domain wall density via AC electric field poling.[240]Therefore,domain engineering addresses a solution for achieving giant piezoelectricity in the PMN–PT system,which offers a useful concept for designing highperformance RE–FE composites. To achieve high-performance RE–FE composites, the interfacial effect plays a very important role in determining structural homogeneity. Therefore, much more effort should be made to advance the RE–FE composites, despite the recent progress in optimizing depolarization temperature, improving Qm, and highperformance electromechanical properties.[241]Future research work should be focused on exploring good overall performances through either structural heterogeneity or domain engineering design in RE–FE composites. The most effective way to introduce LSH in relaxor ferroelectrics is the chemical doping strategy; however, challenges are the optimization of the doping element types, amount, and effectiveness.In addition to that,it is still confronted with a critical challenge to precisely achieve the structural heterogeneity with controlled interfaces.In addition, the optimization of the integration between relaxors and ferroelectrics is still needed to obtain composites for applications with reliability and flexibility.

6.2. Interfacial Effect

In recent years, experimental and theoretical protocols demonstrate the decisive influence of the interfaces on the mechanical/electrical/thermal performance of dielectric composites. Interface modification has become one of the mainstream methods for enhancing the compatibility between inorganic and organic materials and improving the EBDof polymer–ceramic nanocomposites.[242,243]It has been found that small ligands could be useful to tune the surfaces of the fillers,and local electric field concentration can be mitigated by core-shell structure design,[244–246]leading to an improved EBDof the polymer–ceramic composites. In return, the enhancement of EBDcontributes to the high energy density and electrocaloric effect. However, interfacial defects may be formed, such as microvoids and cracks, resulting in uniform microstructure in the nanocomposites and also limiting further enhancement of the breakdown strength.Recently,a new approach via interfacial engineering by constructing a multiscale interface is a simple,yet useful tool for the enhancement of the energy density and efficiency of ceramic–polymer nanocomposite materials.[113]A better understanding of the interfacial effect will be helpful in gaining more structural insights into ferroelectric nanocomposites and assist in designing highperformance nanocomposites. Unfortunately, it is a grand challenge to directly observe the physical and chemical properties of the interfacial regime (such as local polarization, space charge density,[247]chemical mapping of the interfacial coupling, and electric field distribution).Recently, Peng et al.[202]employed a Kelvin probe force microscopy setup (Figure 13a,b) with a nanoscale spatial resolution to detect the polarizations at the interface in P(VDF-TrFE)-BT nanocomposites. They found a high surface potential at the interfaces, as shown in Figure 13c–e. Liu et al.[248]used atomic force microscopy–infrared spectroscopy setup (Figure 13f) to study the chemical mapping in ceramic–polymer nanocomposites, as displayed in Figure 13g–i. New experimental characterization techniques could provide insights into the interfaces of polymer–ceramic nanocomposite systems. Prolonged efforts should be made to disclose the mystery of the relationship between interfacial effect and electrical properties. The novel interface approach is considered as one of the best engineered strategies for high permittivity, high EBD, and high-energy performance polymer-based nanocomposites. Interfacial engineering could play an essential role in designing ceramic–ceramic dielectric composites. Many interfacedirected works were reported over the last 5 years, but the features of these interfaces require practical implications and further understanding. As one example, the interface-related properties under electric fields and the relationship between the components and interfaces demand detailed answers from researchers.

6.3. Performance Predictions

Computational approaches such as finite-element and phase-field have been successfully developed to describe breakdown processes and electric field distribution in dielectric composites. However, it is a major challenge to calculate the permittivity, electrical polarization, piezoelectric response,and the distribution of electric field due to a lot of factors that must be taken into consideration. For example, the finite-element method(FEM)is a useful tool to evaluate the spatial potential and interface charge density distribution in FE nanocomposites. A large increase in energy density was found in BT–PVDF FE composites,[249]which was related to the favorable electric field redistribution through finiteelement simulations, as provided in Figure 14a–c. Shen et al.[250]employed the FEM to explain the critical role of space charges on the electrical properties of polymer composite dielectrics (Figure 14d).FEM has been proven to be successful to access the electric field distribution, breakdown path, and electrical properties of nanocomposite dielectrics. However, different meshes are needed for describing the microstructures, and the cost of numerical calculation significantly increases when the complexity of the composites increased.

Phase-field simulation is suggested to overcome this challenge by solving electrostatic equations in a parallel computing algorithm.[113,251]In a phase-field model, the interphase boundary conditions could be automatically satisfied when simulating the dielectric permittivity,charge density,and local field distribution.It is of interest to employ phase-field modeling to access the breakdown performance in composite systems.Recently,high-throughput phase-field calculation has been utilized to create surrogate models of the performance predictions and properties of ceramic–polymer FE nanocomposites.[41]For instance,it was found that the EBDand breakdown pathway rely on the microstructures of the nanocomposite, as shown in Figure 14e–h.Using high-throughput phase-field model, a PVDF–BT nanocomposite with a sandwich microstructure was designed,which had the enhancement of energy density by 244% with respect to pure PVDF.[41]The phase-field model has also emerged as one of the mesoscale simulation tools for the understanding of grain boundary, phase transitions,microstructure evolution, and dielectric breakdown process in RE–FE composites.[252,253]However, there are plentiful unsettled questions and challenges, such as the connection between the domains and the enhancement of the piezoelectric and dielectric responses,the origin of the relaxation process, and the influence of defects like oxygen vacancies, thermofluctuations, and dynamics of PNRs, deserving more intense investigation. However, the phase-field calculations require a profound knowledge of the physical parameters (in most cases known as ferroelectric order parameters)of the material,most of which are not available.

Figure 13. Advanced characterization techniques for disclosing the interfacial effect. Schematic of a) measuring process and b) working principle of Kelvin Probe Force Microscopy setup. c) Topography signal and d) a 3D image of the topography and e) the surface potential difference (ΔV).[202] Copyright ©2019, John Wiley & Sons. f) Schematic of atomic force microscopy-infrared spectroscopy. g) Topography and chemical maps of P(VDF-TrFE-CFE). h) Local spectra of the sites marked in g). i) Topography and chemical maps of BT-P(VDF-TrFE-CFE) composite.[248] Copyright © 2020, John Wiley & Sons. The size of images in g) and i) is 2 × 2 µm2.

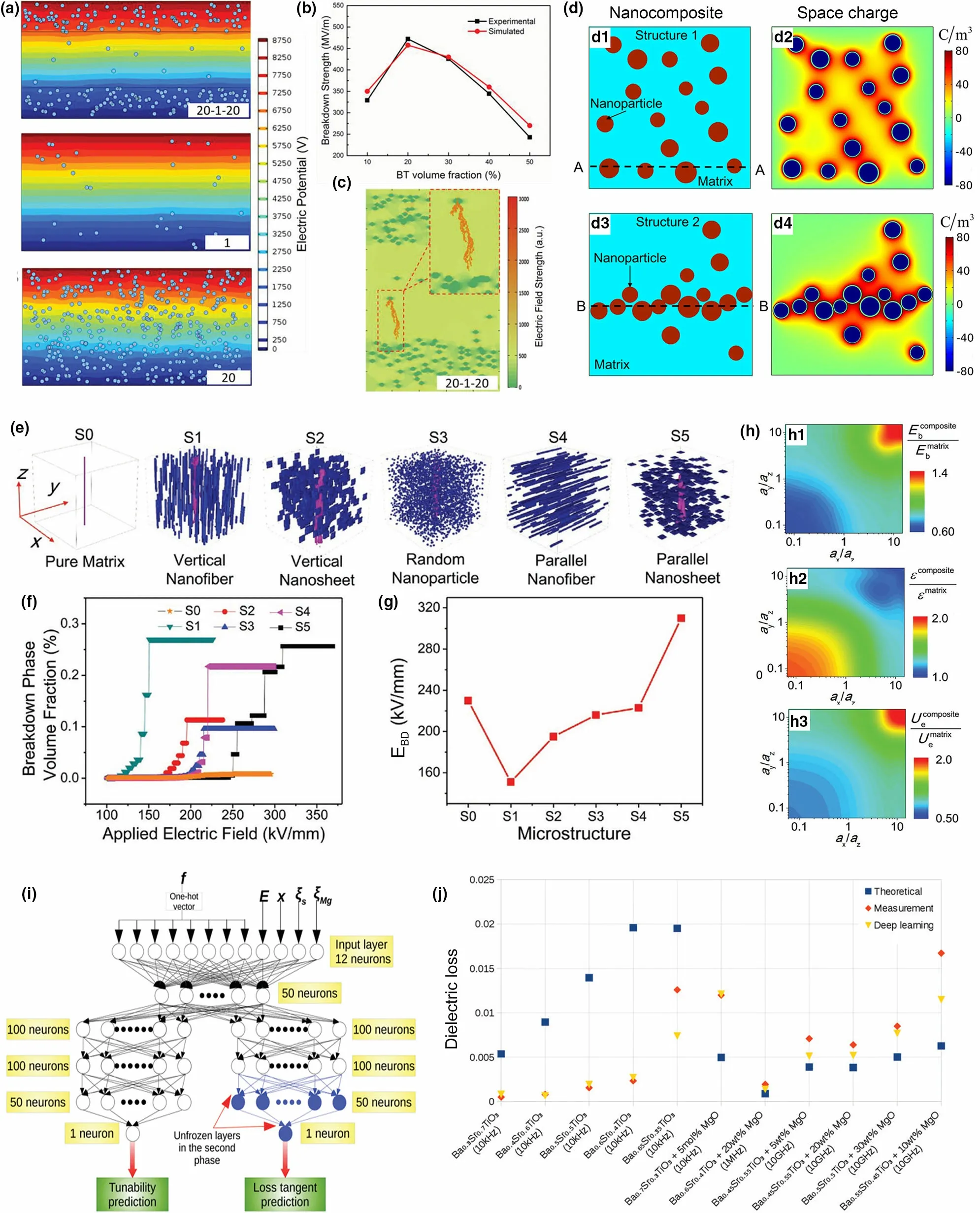
Figure 14. Emerging simulation approaches. a) The electric field distribution in FE BT-PVDF composites. b) Experimental and simulated EBD. c) The breakdown process in BT-PVDF.Ref.[249]Copyright©2015,John Wiley&Sons.d)Schematics of the nanocomposites with randomly distributed(structure 1)and aggregated(structure 2)SrTiO3 nanoparticles and corresponding distributions of space charges.[250]Copyright©2017,AIP Publishing.e–h)Phase-field simulation results of nanocomposites with different breakdown phase morphology.[41]Copyright©2017,John Wiley&Sons.i)Deep neural network and j)comparison of theoretical model simulations,experimental data,and ML predictions of various single-phase materials and composites.[255]Copyright©2020,The Royal Society of Chemistry.

To effectively bypass these calculations, machine learning (ML)frameworks are increasingly being employed to predict material properties (e.g., dielectric constant and loss) and to design and discover novel dielectric composites.[254–258]Despite being useful for the discovery and optimization of new dielectric composites,the integration of machine learning remains a less explored research field. The timely relevance of BT-based piezoelectric materials and polymer-based dielectrics is apparent with the help of the development of accelerated discovery using ML,[251,259]and the notion of ML has been recently employed to predict material properties of dielectric composites.[246]Very recently,the ML framework(Figure 14i)was introduced to calculate the properties of different composite dielectrics.ML results are closer to the experimental results than the simulated data by other methods (see Figure 14j). Currently, ML and high-throughput calculations have not yet been extensively used in the design of ceramic–polymer composite materials.Many efforts need to be made for understanding the mechanisms of dielectric,piezoelectric,electrocaloric,energy performance,and simulating the microstructures of composites by inverting the prediction pipeline using advanced theoretical strategies.[260]

6.4. Working at Elevated Temperature

Dielectric polymers are usually used at low working temperatures,which does not meet the need for energy storage and conversion in automobiles, the military arena, aerospace power systems, and advanced microelectronics.[261–263]For example, the glass transition of the BOPP film is at 105 °C, the maximum working temperature for BOPP polymer.[15]A polymer-based nanocomposite approach is a useful way to enhance the working temperature, but the energy performance of the existing polymer nanocomposite-based dielectrics is still very limited at high temperatures. This is caused by the higher local thermal instability at high temperatures due to the ease of thermal breakdown. The high-record working temperature up to 250 °C has been recently achieved in cross-linked divinyltetramethyldisiloxanebis(benzocyclobutene) nanocomposites with boron nitride nanosheets as the fillers due to the suppression of the electric conduction and improvement of the thermal conductivity.[92]In general, the thermal conductivity of PVDF-based polymer could be largely enhanced with the incorporation of barium strontium titanate nanowires.[264]The low thermal conductivity poses an obstacle to realizing high efficiency in EC devices because most thermal energies of ECE are blocked in EC materials when used at a high frequency.This challenge can be addressed via the nanocomposite approach, for example, thermal conductivity was realized in the PVDF-based nanocomposite materials. The periodical pattern of fillers anchored in a polymer material could contribute to the anisotropic thermal conductivity of the dielectric nanocomposites.[13,264]Further study on the effects of thermal conductivity and electric conduction is needed so that the ceramic–polymer composites can work at higher temperatures.

7. Summary and Outlook

In summary, recent progress including scientific understanding, the aspects of applications and fabrication techniques, and technology demonstrations using polymer-based and ceramic-based FE composites has been reviewed. The area of FE-based dielectric composites for energy storage and conversion applications is experiencing fast growth in recent years and is indeed among one of the hot research pursuits because composites have a distinct advantage of the flexibility of design over other materials.The technology of dielectric composites,in return,would help develop a new approach in materials research (e.g.,topologically polar skyrmions can be stabilized in FE nanocomposites with confined geometry[8]). High performances of energy storage and conversion are the driving force in advanced FE-based dielectric composites. To design composites with high-performance multifunctional properties more than the net sum of the properties of individual components, significant efforts are still required to understand the structure–property relation, performance, and fabrication process of dielectric composites.Composites can undoubtedly generate a new way of thinking and turn the attention of materials scientists to interfacial engineering,with interfaces and surfaces becoming a prime concern of materials science and technology and is emerging as a new area of research.[265–267]

Although manifold improvements in the dielectrics, energy storage,electrocaloric effect, and thermal stability of dielectric composites have been achieved, numerous investigations need to be done as challenges and opportunities persist.The development of dielectric composites will receive considerable attention in the inorganic/organic chemistry community and condensed matter community, including the modeling community. Herein, we highlight some points for upcoming research avenues on scale-bridging optimization of composites for energy storage and conversion. First, environmentally friendly and sustainable materials are highly desirable for both filler and matrix phases in the design of composites.In the future,lead-free dielectric composites with high-performance functional responses should be developed to replace toxic Pb-based materials. Second, the structure; chemical composition,electrical, and mechanical parameters of filler and matrix phases; and interfacial effect should be taken into account to design a dielectric composite. For example, relaxor FEs and FEs with compositions near morphotropic phase boundary exhibit outstanding dielectric,piezoelectric, and electromechanical properties are the material bases for energy systems. Most recently, chirality-induced relaxor features and morphotropic phase boundary have been observed in PVDF-based copolymers,[167,268]which may offer opportunities for optimizing the performances of the polymer material. Many factors are related to the inhomogeneity in a dielectric composite,such as defects,gradients,and interfaces.For example,the introduction of large permittivity fillers into polymers with small permittivity results in inhomogeneous concentrations of the electric field around the fillers,which results in an increased relative permittivity and increased probability of electrical breakdown.Third, the demand for high-performance capacitors and high-efficient coolers to address the limitations of energy devices and systems with high operating temperatures also triggers the researchers to search for composites with high temperature stability, which leads to new challenges with respect to dielectric loss and electrical/thermal conductivity.[269,270]Last but not least, emerging machine learning and highthroughput phase-field calculations are just dawning, which could accelerate the design and discovery of dielectric composites that meet the target property-oriented requirements.

Acknowledgements

H.W., F.Z. and H.Q. contributed equally to this work. This work was financially supported by the State Key Lab of Advanced Metals and Materials (No. 2020-Z16) and the Fundamental Research Funds for the Central Universities (USTB:No. 06500135). Huimin Qiao thanks the National Research Foundation of Korea(No. 2019R1I1A1A01063888) for financial support. Fangping Zhuo would like to thank the Alexander von Humboldt Foundation for financial support. The computing work was supported by USTB MatCom of Beijing Advanced Innovation Center for Materials Genome Engineering. Prof. Q. Zhang also acknowledges the financial support from the Opening Project of National Joint Engineering Research Center for Abrasion Control and Molding of Metal Materials,and Henan Key Laboratory of High-temperature Structural and Functional Materials, Henan University of Science and Technology(Grants No.HKDNM2019013).

Conflict of interest

The authors declare no conflict of interest.

Keywords

composite, dielectric, energy storage and conversion, ferroelectric

Received: May 2, 2021

Revised: June 12, 2021

Published online: June 21, 2021

[1] D. D. L. Chung, Composite materials: Functional Materials for Modern Technologies, Springer Verlag, London 2004.

[2] Prateek, V. K. Thakur, R. Gupta, Chem. Rev. 2016, 116, 4260. https://doi.org/10.1021/acs.chemrev.5b00495

[3] G. G. Raju, Dielectrics in Electric Fields, Marcel Dekker Inc, New York 2003.

[4] A. J. Lovinger. in Developments in Crystalline Polymers—1 (Ed: D. C.Bassett), Springer, Netherlands, 1982, Ch. 5.

[5] K. Rittenmyer, T. Shrout, W. A. Schulze, R. E. Newnham, Ferroelecrrics 1982, 41, 189.

[6] K. Kakimoto, K. Fukata, H. Ogawa, Sens. Actuators, A 2013, 200, 21.

[7] P. Kim, N. M. Doss, J. P. Tillotson, P. J. Hotchkiss, M.-J. Pan, S. R. Marder, J. Li, J. P. Calame, J. W. Perry, ACS Nano 2009, 3, 2581.

[8] Y. Nahas, S. Prokhorenko, L. Louis, Z. Gui, I. Kornev, L. Bellaiche, Nat.Commun. 2015, 6, 8542.

[9] V. G. Shevchenko, S. V. Polschikov, P. M. Nedorezova, A. N. Klyamkina,A. N. Shchegolikhin, A. M. Aladyshev, V. E. Muradyan, Polymer 2012,53, 5330.

[10] L.Yang,H.Ji,K.Zhu,J.Wang,J.Qiu,Compos.Sci.Technol.2016,123,259.

[11] J. Zhang, Z. Pan, F.-F. Guo, W.-C. Liu, H. Ning, Y. B. Chen, M.-H. Lu, B.Yang, J. Chen, S.-T. Zhang, X. Xing, J. R¨odel, W. Cao, Y.-F. Chen, Nat.Common. 2015, 6, 6615.

[12] L. Deng, M. Lin, S. Ji, M. Zhang, Q. Yang, Fu. Prog. Polym. Sci. 2014, 39,627.

[13] Y. Hao, X. Wang, K. Bi, J. Zhang, Y. Huang, L. Wu, P. Zhao, K. Xu, M.Lei, L. Li, Nano Energy 2017, 31, 49.

[14] Q. Li, G. Zhang, F. Liu, K. Han, M. R. Gadinski, C. Xiong, Q. Wang,Energy Environ. Sci. 2015, 8, 922.

[15] M. Guo, J. Jiang, Z. Shen, Y. Lin, C.-W. Nan, Y. Shen, Mater. Today 2019, 29, 49.

[16] X.Huang,B.Sun,Y.Zhu,S.Li,P.Jiang,Prog.Mater.Sci.2019,100,187.

[17] J. Fu, Y. Hou, X. Gao, M. Zheng, M. Zhu, Nano Energy 2018, 52, 391.

[18] C. K. Jeong, C. Baek, A. I. Kingon, K.-I. Park, S.-H. Kim, Small 2018, 14,1704022.

[19] K. V. Lalitha, L. M. Riemer, J. Koruza, J. R¨odel, Appl. Phys. Lett. 2017,111, 022905.

[20] Q. Li, G. Zhang, X. Zhang, S. Jiang, Y. Zeng, Q. Wang, Adv. Mater.2015, 27, 2236.

[21] H. Hu, F. Zhang, S. Luo, J. Yue, C. H. Wang, J. Mater. Chem. A 2020, 8,16814.

[22] J. Shi, D. Han, Z. Li, L. Yang, S.-G. Lu, Z. Zhong, J. Chen, Q. M. Zhang,X. Qian, Joule 2019, 3, 1200.

[23] Y. Chen, J. Qian, J. Yu, M. Guo, Q. Zhang, J. Jiang, Z. Shen, L.-Q. Chen,Y. Shen, Adv. Mater. 2020, 32, 1907927.

[24] G. Zhang, Q. Li, H. Gu, S. Jiang, K. Han, M. R. Gadinski, M. A. Haque,Q. Zhang, Q. Wang, Adv. Mater. 2015, 27, 1450.

[25] H. Zhang, M. A. Marwat, B. Xie, M. Ashtar, K. Liu, Y. Zhu, L.Zhang, P. Fan, C. Samart, Z.-G. Ye, ACS Appl. Mater. Interfaces 2020, 12, 1.

[26] Piezosystem jena GmbH. https://www.piezosystem.com/downloads/ma rketing_material/catalog/, accessed: January, 2021.

[27] J. Park, M. Kim, Y. Lee, H. S. Lee, H. Ko, Sci. Adv. 2015, 1, e1500661.

[28] S.Zhang,F.Li,X.Jiang,J.Kim,J.Luo,X.Geng,Prog.Mater.Sci.2015,68,1.

[29] Z.-Y. Shen, J.-F. Li, R. Chen, Q. Zhou, K. K. Shung, J. Am. Ceram. Soc.2011, 94, 1346.

[30] K.A.Klicker,J.V.Biggers,R.E.Newnham,J.Am.Ceram.Soc.1981,64,5.

[31] Q. M. Zhang, H. Li, M. Poh, F. Xia, Z. Y. Cheng, H. Xu, C. Huang, Nature 2002, 419, 284.

[32] N. Jayasundere, B. V. Smith, J. Appl. Phys. 1993, 73, 2462.

[33] D. J. Bergman, Phys. Rep. 1978, 43, 377.

[34] X. Yang, X. L. Zhao, Q. Li, J. Hu, J. L. He, J. Phys. D: Appl. Phys. 2018,51, 115407.

[35] T. Zakri, J.-P. Laurent, M. Vauclin, J. Phys. D: Appl. Phys. 1998, 31,1589.

[36] L. A. Pauer, IEEE Int. Conv. Rec. 1973, 21, 1.

[37] D. A. G. Bruggeman, Ann. Phys. 1935, 416, 636.

[38] H. Banno, Ferroelectrics 1989, 95, 111.

[39] D. E. Dausch, E. Furman, F. Wang, G. H. Haertling, Ferroelectrics 1996,177, 237.

[40] S. B. Biner, S. Y. Hu, Acta Mater. 2009, 57, 2088.

[41] Z. H. Shen, J. J. Wang, Y. Lin, C.-W. Nan, L.-Q. Chen, Y. Shen, Adv.Mater. 2018, 30, 1704380.

[42] T. Shimada, T. Kitamura, T. Q. Bui, V. H. Dinh, Compos. Commun.2020, 22, 100540.

[43] J. Curie, P. Curie, Compt. Rendus 1880, 91, 294.

[44] J. Valasek, Phys. Rev. 1921, 17, 475.

[45] J. Valasek, Phys. Rev. 1922, 20, 639.

[46] G. Shirane, D. A. Takeda, J. Phys. Soc. Jpn. 1952, 7, 5.

[47] G. Shirane, K. Suzuki, A. Takeda, J. Phys. Soc. Jpn. 1952, 7, 12.

[48] J. Jaffe, H. Jaffe, W. R. Cook, Piezoelectric Ceramics, Academic Press,London 1971.

[49] H. Kawai, Jpn. J. Appl. Phys. 1969, 8, 975.

[50] A. J. Lovinger, Science 1983, 220, 1115.

[51] K. Uchino, in Advanced Piezoelectric Materials: Science and Technology(Ed: K. Uchino), Woodhead Publishing, Sawston, Cambridge, UK 2017,Ch. 9.

[52] M. Latour, J. Electrostatics 1977, 2, 241.

[53] C. Hong, S. Huang, J. Shieh, S. Chen, Macromolecules 2012, 45, 1580.

[54] K. S. Ramadan, D. Sameoto, S. Evoy, Smart. Mater. Struct. 2014, 23,033001.

[55] Y. Liu, Q. Wang, Adv. Sci. 2020, 7, 1902468.

[56] T. Kitayama, S. Sugawara, presented at Professional Report Gr. Inst.Elec. Comm. Eng. Japan, CPM72, Piezoelectric and pyroelectric properties of polymer-ferroelectric composites, 1972 (in Japanese).

[57] R.E.Newnham,D.P.Skinner,L.E.Cross,Mater.Res.Bull.1978,13,525.

[58] V. F. Janas, A. Safari, J. Am. Ceram. Soc. 1995, 78, 2945.

[59] E. K. Akdogan, M. Allahverdi, A. Safari, IEEE Trans. Ultrason. Ferr.2005, 52, 746.

[60] H. Li, Y. Zhou, Y. Liu, L. Li, Y. Liu, Q. Wang, Chem. Soc. Rev. 2021, 50,6369.

[61] T. R. Shrout, W. A. Schulze, J. V. Biggers, Ferroelectrics 1980, 29, 129.

[62] L. P. Curecheriu, M. T. Buscaglia, F. Maglia, U. Anselmi-Tamburini, V.Buscaglia, L. Mitoseriu, Appl. Phys. Lett. 2014, 105, 252901.

[63] D. E. Dausch, E. Furman, F. Wang, G. H. Haertling, Ferroelectrics 1996,177, 221.

[64] D.-S. Lee, S.-J. Jeong, E.-C. Park, I.-S. Song, J. Electroceram. 2006, 17, 505.

[65] D. S. Lee, D. H. Lim, M. S. Kim, K. K. Kim, S. J. Jeong, Appl. Phys. Lett.2011, 99, 062906.

[66] G. Groh, D. J. Franzbach, W. Jo, K. G. Webber, J. Kling, L. A. Schmitt, H.-J.Kleebe,S.-J.Jeong,J.-S.Lee,J.R¨odel,Adv.Funct.Mater.2014,24,356.

[67] O. Furukawa, M. Harata, M. Imai, Y. Yamashita, S. Mukaeda, J. Mater.Sci. 1991, 26, 5838.

[68] V. O. Sherman, A. K. Tagantsev, N. Setter, App. Phys. Lett. 2007, 90,162901.

[69] A.Yoneda,T.Takenaka,K.Sakata,Jpn.J.Appl.Phys.Part 1 1989,28,95.

[70] Z.-M. Dang, J.-K. Yuan, J. W. Zha, T. Zhou, S.-T. Li, G.-H. Hu, Prog.Mater. Sci. 2012, 57, 660.

[71] L. Zhu, J. Phys. Chem. Lett. 2014, 5, 3677.

[72] J. E. Mark, Physical Properties of Polymers Handbook, Springer, New York, USA 2007.

[73] S. Park, T. R. Shrout, J. Appl. Phys. 1804, 1997, 82.

[74] S. Zhang, F. Li, J. Appl. Phys. 2012, 111, 031301.

[75] F. Zhuo, D. Damjanovic, Q. Li, Y. Zhou, Y. Ji, Q. Yan, Y. Zhang, Y.Zhou, X. Chu, Mater. Horiz. 2019, 6, 1699.

[76] J. Li, J. Li, H.-H. Wu, S. Qin, X. Su, Y. Wang, X. Lou, D. Guo, Y. Su, L.Qiao, Y. Bai, ACS Appl. Mater. Interfaces 2020, 12, 45005.

[77] F. Zhuo, H. Qiao, J. Zhu, S. Wang, Y. Bai, X. Mao, H.-H. Wu. Chin.Chem. Lett. 2021, 32(7), 2097.

[78] X. Hao, J. Zhai, L. B. Kong, Z. Xu, Prog. Mater. Sci. 2014, 63, 1.

[79] S. Liu, M. Tian, L. Zhang, Y. Lu, T. W. Chan, N. Ning, J. Mater. Sci.2016, 51, 2616.

[80] G. Zhang, D. Brannum, D. Dong, L. Tang, E. Allahyarov, S. Tang, K.Kodweis, J.-K. Lee, L. Zhu, Chem. Mater. 2016, 28, 4646.

[81] R. H. Oppermann, Dielectric Phenomena in High Voltage Cables,McGraw-Hill Book Company, Pittsburgh 1937.

[82] N. Zebouchi, M. Bendaoud, R. Essolbi, D. Malec, B. Ai, H. T. Giam, J.Appl. Phys. 1996, 79, 2497.

[83] S. Li, G. Yin, G. Chen, J. Li, S. Bai, L. Zhong, Y. Zhang, Q. Lei, Dielectr.Electr. Insul. 2010, 17, 1523.

[84] F. Zhuo, C.-H. Yang, Phys. Rev. B 2020, 102, 214112.

[85] X. Yu, Y. Hou, H. Zhao, J. Fu, M. Zheng, M. Zhu, J. Mater. Chem. C 2019, 7, 3479.

[86] Piezoelectric Devices Market. https://www.marketsandmarkets.com/Ma rket-Reports/piezoelectric-devices-market-256019882.html,accessed:January, 2020.

[87] W. J. Sarjeant, I. W. Clelland, R. A. Price, Proc. IEEE 2001, 89, 846.

[88] K.-C. Kao, Dielectric Phenomena in Solids: With Emphasis on Physical Concepts of Electronic Processes, Elsevier Academic Press, Boston, MA 2004.

[89] E. Baer, L. Zhu, Macromolecules 2017, 50, 2239.

[90] M. Mackey, D. E. Schuele, L. Zhu, L. Flandin, M. A. Wolak, J. S. Shirk,A. Hiltner, E. Baer, Macromolecules 1954, 2012, 45.

[91] Z. Li, X. Chen, C. Zhang, E. Baer, D. Langhe, M. Ponting, M. Brubaker,T. Hosking, R. Li, M. Fukuto, L. Zhu, A. C. S. Appl, Polym. Mater. 2019,1, 867.

[92] Z. Zhou, C. Carr, M. Mackey, K. Yin, D. Schuele, L. Zhu, E. Baer, J.Polym. Sci. Pt. B-Polym. Phys. 2013, 51, 978.

[93] J. Jiang, Z. Shen, J. Qian, Z. Dan, M. Guo, Y. Lin, C.-W. Nan, L. Chen, Y.Shen, Energy Storage Mater. 2019, 18, 213.

[94] C.Yuan,Y.Zhou,Y.Zhu,J.Liang,S.Wang,S.Peng,Y.Li,S.Cheng,M.Yang,J.Hu,B.Zhang,R.Zeng,J.He,Q.Li,Nat.Commun.2020,11,3919.

[95] M. Ma, L. Guo, D. G. Anderson, R. Langer, Science 2013, 339, 186.

[96] T. Vijayakanth, F. Ram, B. Praveenkumar, K. Shanmuganathan, R.Boomishankar, Chem. Mater. 2019, 31, 5964.

[97] S. Liao, Z. Shen, H. Pan, X. Zhang, Y. Shen, Y.-H. Lin, C.-W. Nan, J.Mater. Chem. C 2017, 5, 12777.

[98] N. Luo, K. Han, F. Zhuo, C. Xu, G. Zhang, L. Liu, X. Chen, C. Hu, H.Zhou, Y. Wei, J. Mater. Chem. A 2019, 7, 14118.

[99] X. Yang, F. Zhuo, C. Wang, Y. Liu, Z. Wang, H. Tailor, C. He, X. Long, J.Mater. Chem. A 2019, 7, 8414.

[100] D. Ai, H. Li, Y. Zhou, L. Ren, Z. Han, B. Yao, W. Zhou, L. Zhao, J. Xu,Q. Wang, Adv. Energy Mater. 2020, 10, 1903881.

[101] Q. Li, L. Chen, M. R. Gadinski, S. Zhang, G. Zhang, H. U. Li, E. Iagodkine, A. Haque, L.-Q. Chen, T. N. Jackson, Q. Wang, Nature 2015, 523,576.

[102] Y. Wang, Y. Xia, Adv. Mater. 2013, 25, 5336.

[103] C. Guan, X. Liu, W. Ren, X. Li, C. Cheng, J. Wang, Adv. Energy Mater.2017, 7, 1602391.

[104] T. Yang, H.-J. Liu, F. Bai, E.-H. Wang, J.-H. Chen, K.-C. Chou, X.-M. Hou,Int. J. Min. Met. Mater. 2020, 27, 220.

[105] J. B. Goodenough, Energy Storage Mater. 2015, 1, 158.

[106] A. Khaligh, Z. Li, IEEE Trans. Veh. Technol. 2010, 59, 2806.

[107] X. Han, Y. Gong, K. Fu, X. He, G. T. Hitz, J. Dai, A. Pearse, B. Liu, H.Wang, G. Rubloff, Y. Mo, V. Thangadurai, E. D. Wachsman, L. Hu, Nat.Mater. 2017, 16, 572.

[108] T. D. Huan, S. Boggs, G. Teyssedre, C. Laurent, M. Cakmak, S. Kumar,R. Ramprasad, Prog. Mater. Sci. 2016, 83, 236.

[109] P. Hu, W. Sun, M. Fan, J. Qian, J. Jiang, Z. Dan, Y. Lin, C.-W. Nan, M.Li, Y. Shen, Appl. Surf. Sci. 2018, 458, 743.

[110] P. Wang, Z. Pan, W. Wang, J. Hu, J. Liu, J. Yu, J. Zhai, Q. Chi, Z. Shen, J.Mater. Chem. A 2021, 9, 3530.

[111] B. Luo, X. Wang, E. Tian, Y. Yao, Z. Cai, K. Xi, H. Song, H. Song, B. Li,L. Li, Mater. Today Energy 2019, 12, 136.

[112] Q. Chi, Y. Zhou, Y. Feng, Y. Cui, Y. Zhang, T. Zhang, Q. Chen, Mater.Today Energy 2020, 18, 100516.

[113] X. Zhang, J. Jiang, Z. Shen, Z. Dan, M. Li, Y. Lin, C.-W. Nan, L. Chen, Y.Shen, Adv. Mater. 2018, 30, 1707269.

[114] The Future of Cooling Opportunities for Energy-Efficient Air Conditioning, https://www.iea.org/reports/the-future-of-cooling, accessed:May, 2018.

[115] G. J. Velders, D. W. Fahey, J. S. Daniel, M. McFarland, S. O. Andersen,Proc. Natl. Acad. Sci. USA 2009, 106, 10949.

[116] H. H. Wu, J. Zhu, T. Y. Zhang, Nano Energy 2015, 16, 419

[117] B. Russ, A. Glaudell, J. J. Urban, M. L. Chabinyc, R. A. Segalman, Nat.Rev. Mater. 2016, 1, 16050.

[118] Z. Li, J. Li, H. H. Wu, J. Li, S. Wang, S. Qin, S. Yang, L. Qiao, D. Guo, Y.Bai, Acta Mater. 2020, 191, 13.

[119] F. Zhuo, Q. Li, J. Gao, Y. Ji, Q. Yan, Y. Zhang, H.-H. Wu, X.-Q. Xi, X.Chu, W. Cao, ACS Appl. Mater. Interfaces 2018, 10, 11747.

[120] H.-H. Wu, J. Zhu, T.-Y. Zhang, RSC Adv. 2015, 5, 37476.

[121] A. S. Mischenko, Q. Zhang, J. F. Scott, R. W. Whatmore, N. D. Mathur,Science 2006, 311, 1270.

[122] B. Neese, B. Chu, S. G. Lu, Y. Wang, E. Furman, Q. M. Zhang, Science 2008, 321, 821.

[123] V. Franco, J. S. Bl´azquez, J. J. Ipus, J. Y. Law, L. M. Moreno-Ram´ırez, A.Conde, Prog. Mater. Sci. 2018, 93, 112.

[124] J. Tuˇsek, K. Engelbrecht, D. Eriksen, S. Dall’Olio, J. Tuˇsek, N. Pryds, Nat.Energy 2016, 1, 16134.

[125] B. Li, Y. Kawakita, S. Ohira-Kawamura, T. Sugahara, H. Wang, J. Wang,Y. Chen, S. I. Kawaguchi, S. Kawaguchi, K. Ohara, K. Li, D. Yu, R. Mole,T. Hattori, T. Kikuchi, S.-I. Yanoi, Z. Zhang, Z. Zhang, W. Ren, S. Lin,O. Sakata, K. Nakajima, Z. Zhang, Nature 2019, 567, 506.

[126] X. Moya, S. Kar-Narayan, N. D. Mathur, Nat. Mater. 2014, 13, 439.

[127] X. Moya, N. D. Mathur, Science 2020, 370, 797.

[128] H. H. Wu, R. E. Cohen, Phys. Rev. B 2017, 96, 054116.

[129] X. S. Qian, H. J. Ye, Y. T. Zhang, H. Gu, X. Li, C. A. Randall, Q. M.Zhang, Adv. Funct. Mater. 2014, 24, 1300.

[130] S. Crossley, T. Usui, B. Nair, S. Kar-Narayan, X. Moya, S. Hirose, A.Ando, N. D. Mathur, Appl. Phys. Lett. 2016, 108, 032902.

[131] G. Zhang, X. Zhang, T. Yang, Q. Li, L. Q. Chen, S. Jiang, Q. Wang, ACS Nano 2015, 9, 7164.

[132] X. Li, S.-Q. Lu, X.-Z. Chen, H. Gu, X.-S. Qian, Q. M. Zhang, J. Mater.Chem. C 2013, 1, 23.

[133] M. Valant, Prog. Mater. Sci. 2012, 57, 980.

[134] T. Correlia, Q. Zhang, Electrocaloric Materials: New Generation of Coolers, Springer, Berlin, Heidelberg, Germany 2014.

[135] Y. Wang, Z. Zhang, T. Usui, M. Benedict, S. Hirose, J. Lee, J. Kalb, D.Schwartz, Science 2020, 370, 129.

[136] A. Torell´o, P. Lheritier, T. Usui, Y. Nouchokgwe, M. G´erard, O. Bouton,S. Hirose, E. Defay, Science 2020, 370, 125.

[137] X. Moya, E. Defay, N. D. Mathur, S. Hirose, MRS Bull. 2018, 43, 291.

[138] A.Kumar,A.Thakre,D.-Y.Jeong,J.Ryu,J.Mater.Chem.C 2019,7,6836.

[139] B. Nair, T. Usui, S. Crossley, S. Kurdi, G. G. Guzm´an-Verri, S. Moya, S.Hirose, N. D. Mathur, Nature 2019, 575, 468.

[140] X.Moya,E.Stern-Taulats,S.Crossley,D.Gonz´alez-Alonso,S.Kar-Narayan,A.Planes,L.Ma˜nosa,N.D.Mathur,Adv.Mater.2013,25,1360.

[141] A. I. Karchevskii, Sov. Phys. Solid State 1962, 3, 2249.

[142] B. Roˇziˇc, M. Kosec, H. Urˇsiˇc, J. Holc, B. Maliˇc, Q. M. Zhang, R. Blinc, R.Pirc, Z. Kutnjak, J. Appl. Phys. 2011, 110, 064118.

[143] S. G. Lu, B. Roˇziˇc, Q. M. Zhang, Z. Kutnjak, X. Li, E. Furman, L. J.Gorny, M. Lin, B. Maliˇc, M. Kosec, R. Blinc, R. Pirc, Appl. Phys. Lett.2010, 97, 162904.

[144] Y. Bai, G. P. Zheng, K. Ding, L. Qiao, S. Q. Shi, D. Guo, J. Appl. Phys.2010, 110, 094103.

[145] Y. Liu, H. Strozyk, B. Dkhil, E. Defay, Appl. Phys. Lett. 2016, 109,212902.

[146] Y. Bai, K. Ding, G.-P. Zheng, S.-Q. Shi, L. Qiao, Phys. Status Solidi A 2012, 209, 941.

[147] B. Peng, H. Fan, Q. Zhang, Adv. Funct. Mater. 2013, 23, 2987.

[148] X. Li, X. Qian, H. Gu, X. Chen, S. G. Lu, M. Lin, F. Bateman, Q. M.Zhang, Appl. Phys. Lett. 2012, 101, 132903.

[149] J. Qian, R. Peng, Z. Shen, J. Jiang, F. Xue, T. Yang, L. Chen, Y. Shen,Adv. Mater. 2018, 31, 1801949.

[150] Y.-C. Lu, J. Yu, J. Huang, S. Yu, X. Zeng, R. Sun, C.-P. Wong, Appl. Phys.Lett. 2019, 114, 233901.

[151] G. H. Haertling, J. Am. Ceram. Soc. 1999, 82, 797.

[152] F. Felten, G. A. Schneider, J. M. Salda˜na, S. V. Kalinin, J. Appl. Phys.2004, 96, 563.

[153] D. K. Khatua, N. P. Maria Joseph Raj, G. Khandelwal, A. N. Rao, S.-J.Kim, Mater. Today Energy 2021, 20, 100679.

[154] A. Jain, K. J. Prashanth, A. K. Sharma, A. Jain, P. N. Rashmi, Polym. Eng.Sci. 2015, 55, 1589.

[155] D. Prateek, N. Singh, A. Garg, R. K. Gupta, Compos. Sci. Technol. 2019,174, 158.

[156] C. G. Wu, P. Li, W. B. Luo, J. Meng, X. Y. Sun, Y. Shuai, W. L. Zhang,Mater. Res. Innov. 2014, 18, S2-229.

[157] K. Shi, B. Chai, H. Zou, P. Shen, B. Sun, P. Jiang, Z. Shi, X. Huang, Nano Energy 2021, 80, 105515.

[158] K. K. Sappati, S. Bhadra, IEEE Sens. J. 2020, 20, 4610.

[159] X.Gao,M.Zheng,X.Yan,J.Fu,Y.Hou,M.Zhu,Nanoscale 2020,12,5175.

[160] H. Zhao, Y. Hou, X. Yu, M. Zheng, M. Zhu, J. Mater. Chem. A 2021, 9,2284.

[161] D. B. Deutz, PhD Thesis, Delft University of Technology (Delft). October, 2017.

[162] H. Li, C. Tian, Z. D. Deng, Appl. Phys. Rev. 2014, 1, 041301.

[163] N. K. James, D. B. Deutz, R. K. Bose, S. van der Zwaag, W. A. Groen, J.Am. Ceram. Soc. 2016, 99, 3957.

[164] K. N. Kim, J. Chun, S. A. Chae, C. W. Ahn, I. W. Kim, S.-W. Kim, Z. L.Wang, J. M. Baik, Nano Energy 2015, 14, 87.

[165] D. B. Deutz, N. T. Mascarenhas, J. B. J. Schelen, D. M. de Leeuw, S. van der Zwaag, P. Groen, Adv. Funct. Mater. 2017, 27, 1700728.

[166] S. Bauer, F. Bauer, in Piezoelectricity: evolution and future of a technology, Vol. 114 (Eds: W. Heywang, K. Lubitz, W. Wersing) Springer Science & Business Media, Germany 2008, Ch 6.

[167] Y. Liu, H. Aziguli, B. Zhang, W. Xu, W. Lu, J. Bernholc, Q. Wang, Nature 2018, 562, 96.

[168] J. R¨odel, K. G. Webber, R. Dittmer, W. Jo, M. Kimura, D. Damjanovic, J.Eur. Ceram. Soc. 2015, 35, 1659.

[169] D. A. van den Ende, W. A. Groen, S. van der Zwaag, J. Intel. Mater.Syst. Str. 2013, 24, 2262.

[170] X. Fang, J. He, Y. Zhang, Sensor Mater. 2016, 28, 681.

[171] L. M. Riemer, K. V. Lalitha, X. Jiang, N. Liu, C. Dietz, R. W. Stark, P. B.Groszewicz, G. Buntkowsky, J. Chen, S.-T. Zhang, J. R¨odel, J. Koruza,Acta Mater. 2017, 136, 271.

[172] M. Acosta, N. Novak, V. Rojas, S. Patel, R. Vaish, J. Koruza, G. A. Rossetti, J. R¨odel, Appl. Phys. Rev. 2017, 4, 041305.

[173] J. Yin, Y. Wang, Y. Zhang, B. Wu, J. Wu, Acta Mater. 2018, 158, 269.

[174] K. V. Lalitha, M. Hinterstein, K.-Y. Lee, T. Yang, L.-Q. Chen, P. B. Groszewicz, J. Koruza, J. R¨odel, Phys. Rev. B 2020, 101, 174108.

[175] J. A. Weimer, AIAA/IEEE Dig. Avion. Syst. Conf. IEEE 1993.

[176] P. Ren, J. Wang, Y. Wang, K. V. Lalitha, G. Zhao, J. Eur. Ceram. Soc.2020, 40, 2964.

[177] Y. Yan, J. E. Zhou, D. Maurya, Y. U. Wang, S. Priya, Nat. Commun.2016, 7, 13089.

[178] J. Hao, W. Li, J. Zhai, H. Chen, Mat. Sci. Eng. R 2019, 135, 1.

[179] S.-T. Zhang, A. B. Kounga, W. Jo, C. Jamin, K. Seifert, T. Granzow, J.R¨odel, D. Damjanovic, Adv. Mater. 2009, 21, 4716.

[180] F. Zhuo, Q. Li, Y. Zhou, Y. Ji, Q. Yan, Y. Zhang, X. Xi, X. Chu, W. Cao,Acta Mater. 2018, 148, 28.

[181] R. E. Newnham, Properties of Materials: Anisotropy, Symmetry, Structure, Oxford University Press, UK 2004.

[182] J. Watson, G. Castro, Analog Dialogue 2012, 46, 1.

[183] T. R. Shrout, S. Zhang, J. Electroceram. 2007, 19, 113.

[184] F. Fang, Y. Ji, Z. Zhang, Y. Yang, C. Liu, D. Wang, L. Zhang, J. Gao, X.Ren, NPG Asia Mater. 2018, 10, 1029.

[185] K. T. Seifert, J. R¨odel, J. Am. Ceram. Soc. 2010, 93, 1392.

[186] H. Zhang, C. Groh, Q. Zhang, W. Jo, K. Webber, J. R¨odel, Adv. Electron Mater. 2015, 1, 1500018.

[187] T. Li, X. Lou, X. Ke, S. Cheng, S. Mi, X. Wang, J. Shi, X. Liu, G. Dong, H.Fan, Y. Wang, X. Tan, Acta Mater. 2017, 128, 337.

[188] W. Bai, X. Zhao, Y. Ding, L. Wang, P. Zheng, J. Hao, J. Zhai, Adv. Electron Mater. 2020, 6, 2000332.

[189] T. Tsurumi, K. Soejima, T. Kamiya, M. Daimon, Jpn. J. Appl. Phys. 1959,1994, 33.

[190] X. Liu, X. Tan, Adv. Mater. 2016, 28, 574.

[191] H. Zhang, P. Xu, E. Patterson, J. Zang, S. Jiang, J. R¨odel, J. Eur. Ceram.Soc. 2015, 35, 2501.

[192] H. Cui, R. Hensleigh, D. Yao, D. Maurya, P. Kumar, M. Kang, S. Priya,X. Zheng, Nat. Mater. 2019, 18, 234.

[193] S. Priya, S. Nahm, Lead-Free Piezoelectrics, Springer, New York, USA 2011.

[194] W. R. McCall, K. Kim, C. Heath, G. L. Pierre, D. J. Sirbuly, ACS Appl.Mater. Inter. 2014, 6, 19504.

[195] K. Kim, W. Zhu, X. Qu, C. Aaronson, W. R. McCall, S. Chen, D. J. Sirbuly, ACS Nano 2014, 8, 9799.

[196] C. R. Bowen, A. Perry, A. C. F. Lewis, H. Kara, J. Eur. Ceram. Soc. 2004,24, 541.

[197] J. Wang, N. Nie, C. Lan, G. Wang, X. Dong, X. Chen, F. Gao, H. He,Ceramics Int. 2013, 39, 3915.

[198] I. Babu, G. de With, Composites Sci. Technol. 2014, 91, 91.

[199] L. Fang, J. Li, Z. Zhu, S. Orrego, S. Kang, J. Mater. Res. 2018, 33, 330.

[200] Y. Sun, Y. Chang, J. Wu, Y. Liu, L. Jin, S. Zhang, B. Yang, W. Cao, J Mater. Chem. A 2019, 7, 3603.

[201] F. Li, S. Zhang, D. Damjanovic, L.-Q. Chen, T. R. Shrout, Adv. Funct.Mater. 2018, 28, 1801504.

[202] S. Peng, X. Yang, Y. Yang, S. Wang, Y. Zhou, J. Hu, Q. Li, J. He, Adv.Mater. 2019, 31, 1807722.

[203] Q. Liu, Y. Zhang, J. Gao, Z. Zhou, H. Wang, K. Wang, X. Zhang, L. Li,J.-F. Li, Energy Environ. Sci. 2018, 11, 3531.

[204] J.Fu,Y.Hou,M.Zheng,M.Zhu,ACS Appl.Mater.Interfaces 2020,12,9766.

[205] J. Mundy, C. A. Heikes, B. F. Grosso, D. F. Segedin, Z. Wang, B. H.Goodge, Q. N. Meier, C. T. Nelson, B. Prasad, L. F. Kourkoutis, W. D.Ratcliff, N. A. Spaldin, R. Ramesh, D. G. Schlom, arXiv preprint arXiv:1812.09615.

[206] P. Ren, J. Wang, J. He, Y. Wang, H. Yuan, Y. Hao, T. Fr¨omling, Y. Wan,Y. Shi, G. Zhao, Adv. Electronic Mater. 2020, 6, 1901429.

[207] M. H¨ofling, S. Steiner, A.-P. Hoang, I.-T. Seo, T. Fr¨omling, J. Mater.Chem. C 2018, 6, 4769.

[208] Y. Wang, J. Hu, Y. Lin, C.-W. Nan, NPG Asia Mater. 2010, 2, 61.

[209] Z. Chu, M. PourhosseiniAsl, S. Dong, J. Phys. D: Appl. Phys. 2018, 51,243001.

[210] A. Molinari, H. Hahn, R. Kruk, Adv. Mater. 2019, 31, 1806662.

[211] M. T. Le, L. V. Lich, T. Shimada, T. Kitamura, G. T. Nguyen, V. H. Dinh,Appl. Phys. Lett. 2021, 118, 052905.

[212] A. Tsurumaki-Fukuchi, H. Yamada, A. Sawa, Appl. Phys. Lett. 2013,103, 152903.

[213] C. Wang, Y. Zhang, B. Zhang, B. Wang, J. Zhang, L. Chen, Q. Zhang, Z.Wang, K. Ren, Adv. Sci. 2021, 8, 2004554.

[214] B. Wang, Y. Gu, S. Zhang, L. Chen, Prog. Mater. Sci. 2019, 106, 100570.

[215] W. Zhu, J. Fu, N. Li, L. Cross, Appl. Phys. Lett. 2006, 89, 192904.

[216] J. K. Y. Lee, N. Chen, S. Peng, L. Li, L. Tian, N. Thakor, S. Ramakrishna,Prog. Polym. Sci. 2018, 86, 40.

[217] J. Guo, H. Guo, A. L. Baker, M. T. Lanagan, E. R. Kupp, G. L. Messing,C. A. Randall, Angew. Chem. Int. Ed. 2016, 128, 11629.

[218] B. G. Compton, J. A. Lewis, Adv. Mater. 2014, 26, 5930.

[219] X. Wang, M. Jiang, Z. Zhou, J. Gou, D. Hui, Compos. Part B: Eng. 2017,110, 442.

[220] F. Castles, D. Isakov, A. Lui, Q. Lei, C. Dancer, Y. Wang, J. Janurudin, S.Speller, C. Grovenor, P. Grant, Sci. Rep. 2016, 6, 22714.

[221] M. Zastrow, Nature 2020, 578, 20.

[222] M. Skylar-Scott, J. Mueller, C. Visser, J. Lewis, Nature 2019, 575, 330.

[223] M. Regehly, Y. Garmshausen, M. Reuter, N. K¨onig, E. Israel, D.Kelly, C.-Y. Chou, K. Koch, B. Asfari, S. Hecht, Nature 2020, 588,620.

[224] S. Peng, G. Jin, L. Li, K. Li, M. Srinivasan, S. Ramakrishna, J. Chen, Chem.Soc. Rev. 2016, 45, 1225.

[225] W. Xu, Y. Ding, S. Jiang, J. Zhu, W. Ye, Y. Shen, H. Hou, Eur. Polym. J.2014, 59, 129.

[226] H. Liu, Y. Shen, Y. Song, C.-W. Nan, Y. Lin, X. Yang, Adv. Mater. 2011,23, 5104.

[227] J. Jiang, X. Zhang, Z. Dan, J. Ma, Y. Lin, M. Li, C.-W. Nan, Y. Shen, ACS Appl. Mater. Interfaces 2017, 9, 29717.

[228] R.M.German,Sintering Theory and Practice,Wiley,New York,USA 1996.

[229] J. Guo, X. Zhao, T. Beauvoir, J.-H. Seo, S. Berbano, A. Baker, C. Azina,C. A. Randall, Adv. Funct. Mater. 2018, 28, 1801724.

[230] F. Bouville, A. Studart, Nat. Commun. 2017, 8, 14655.

[231] J. Gonzalez-Julian, K. Neuhaus, M. Bernemann, S. J. J. P. Da Silva, A.Laptev, M. Brama, O. Guillon, Acta Mater. 2018, 144, 116.

[232] D. Wang, D. Zhou, S. Zhang, Y. Vardaxoglou, W. Whittow, D. Cadman,I. Reaney, ACS Sustain. Chem. Eng. 2018, 6, 2438.

[233] J. Guo, N. Pfeiffenberger, A. Beese, A. Rhoades, L. Gao, A. Baker, K.Wang, A. Bolvari, C. Randall, ACS Appl. Nano Mater. 2018, 1, 3837.

[234] K. D. Hermanson, S. O. Lumsdon, J. P. Williams, E. W. Kaler, O. D.Velev, Science 2001, 294, 1082.

[235] H.Wu,W.F.Zhao,H.W.Hu,G.H.Chen,J.Mater.Chem.2011,21,8626.

[236] D. S. Kim, C. Baek, H. J. Ma, D. K. Kim, Ceram. Int. 2016, 42, 7141.

[237] V. Tomer, C. A. Randall, J. Appl. Phys. 2008, 104, 074106.

[238] H. Tang, Y. Lin, H. A. Sodano, Adv. Energy Mater. 2012, 2, 469.

[239] J. Martin, A. Iturrospe, A. Cavallaro, A. Arbe, N. Stingelin, T. A.Ezquerra, C. Mijangos, A. Nogales, Chem. Mater. 2017, 29, 3515.

[240] C. Qiu, B. Wang, N. Zhang, S. Zhang, J. Liu, D. Walker, Y. Wang, H.Tian, T. R. Shrout, Z. Xu, L.-Q. Chen, F. Li, Nature 2020, 577, 350.

[241] H. Y. Hwang, Y. Iwasa, M. Kawasaki, B. Keimer, N. Nagaosa, Y. Tokura,Nat. Mater. 2012, 11, 103.

[242] H. Luo, X. Zhou, C. Ellingford, Y. Zhang, S. Chen, K. Zhou, D. Zhang,C. R. Bowen, C. Wan, Chem. Soc. Rev. 2019, 48, 4424.

[243] Z. Pan, L. Yao, J. Zhai, X. Yao, H. Chen, Adv. Mater. 2018, 30, 1705662.

[244] H. Li, D. Ai, L. Ren, B. Yao, Z. Han, Z. Shen, J. Wang, L.-Q. Chen, Q.Wang, Adv. Mater. 2019, 31, 1900875.

[245] L. Xie, X. Huang, Y. Huang, K. Yang, P. Jiang, ACS Appl. Mater. Interfaces 2013, 5, 1747.

[246] X. Huang, P. Jiang, Adv. Mater. 2015, 27, 546.

[247] H.Li,L.Wang,Y.Zhu,P.Jiang,X.Huang.Chin.Chem.Lett.2021,32,2229.

[248] Y. Liu, T. Yang, B. Zhang, T. Williams, Y.-T. Lin, L. Li, Y. Zhou, W. Lu, S.H.Kim,L.-Q.Chen,J.Bernholc,Q.Wang,Adv.Mater.2020,32,2005431.

[249] Y. Wang, J. Cui, Q. Yuan, Y. Niu, Y. Bai, H. Wang, Adv. Mater. 2015, 27,6658.

[250] Z.-H. Shen, J.-J. Wang, X. Zhang, Y. Lin, C.-W. Nan, L.-Q. Chen, Y. Shen,Appl. Phys. Lett. 2017, 111, 092901.

[251] Z.-H. Shen, J.-J. Wang, J.-Y. Jiang, S. Huang, Y.-H. Lin, C.-W. Nan, L.-Q.Chen, Y. Shen, Nat. Commun. 1843, 2019, 10.

[252] S. Wang, A. Ayrikyan, K. G. Webber, H. Zhang, B.-X. Xu, Adv. Electron Mater. 2019, 5, 1800710.

[253] S. Choudhury, Y. Li, I. C. Krill, L. Chen, Acta. Mater. 2007, 55, 1415.

[254] C. Chen, G. Gu, MRS Commun. 2019, 9, 556.

[255] N. Liu, A. Ihalage, H. Zhang, H. Giddens, H. Yan, Y. Hao, J. Mater.Chem. C 2020, 8, 10352.

[256] R. Batra, L. Song, R. Ramprasad. Nat. Rev. Mater. https://doi.org/10.1038/s41578-020-00255-y

[257] A. Chen, X. Zhang, Z. Zhou, InfoMat 2020, 2, 553.

[258] W. Sha, Y. Li, S. Tang, J. Tian, Y. Zhao, Y. Guo, W. Zhang, X. Zhang, S.Lu, Y.-C. Cao, S. Cheng, InfoMat 2021, 3, 353.

[259] R. Yuan, Z. Liu, P. Balachandran, D. Xue, Y. Zhou, X. Ding, J. Sun, D.Xue, T. Lookman, Adv. Mater. 2018, 30, 1702884.

[260] J. I. Roscow, R. W. C. Lewis, J. Taylor, C. R. Bowen, Acta Mater. 2017,128, 207.

[261] R. W. Johnson, J. L. Evans, P. Jacobsen, J. R. Thompson, M. Christophe,IEEE Trans. Electron Packag. Manuf. 2004, 27, 164.

[262] Q. Li, F. Liu, T. Yang, M. R. Gadinski, G. Zhang, L.-Q. Chen, Q. Wang,Proc. Natl. Acad. Sci. USA 2016, 113, 9995.

[263] H.Li,L.Ren,D.Ai,Z.Han,Y.Liu,B.Yao,Q.Wang,InfoMat 2020,2,389.

[264] G. Zhang, B. Fa, P. Zhao, Z. Hu, Y. Liu, F. Liu, S. Jiang, S. Zhang, H. Li,Q. Wang, ACS Appl. Energy Mater. 2018, 1, 1344.

[265] B. Xu, S. Qi, M. Jin, X. Cai, J. Ma, Chin. Chem. Lett. 2019, 30, 2053.

[266] B. Y. Zhou, S. J. Fan, Y. C. Fan, Q. Zheng, X. Zhang, W. Jiang, L. J.Wang, Rare Met. 2020, 39, 513.

[267] C. Zhao, Y. Huang, J. Wu, InfoMat 2020, 2, 1163.

[268] Y. Liu, B. Zhang, W. Xu, A. Haibibu, Z. Han, W. Lu, J. Bernholc, Q.Wang, Nat. Mater. 2020, 19, 1169.

[269] S.Chen,X.Lv,X.Han,H.Luo,C.Bowen,D.Zhang,Polym.Chem.2018,9,548.

[270] M. X. Zhu, Q. C. Yu, H. G. Song, T. X. Chen, J. M. Chen, A. C. S. Appl,Energy Mater. 2021, 4, 1449.

[271] W. B. Harrison, presented at Proc. Workshop on Sonar Transducer Materials, Naval Research Laboratory 1976.

[272] J.R.Giniewicz,K.Duscha,R.E.Newnham,A.Safari,0-3 Composites for Hydrophone Applications,IEEE Int.Symp.Appl.Ferroelect.Bethlehem,PA 1986.

[273] A. Safari, V. F. Janas, U.S. Patent, 5,539,965. 1996.

[274] J. Fousek, L. E. Cross, D. B. Litvin, Mater. Lett. 1999, 39, 287.

[275] L. Rayleigh, Philos. Mag. Ser. 1892, 5, 481.

[276] K. Lichtenecker, Physik. Zeitschr. 1929, 30, 805.

[277] J. C. Maxwell, Electricity and Magnetism, Clarendon Press, Oxford, UAS 1982.

[278] R. Landauer, J. Appl. Phys. 1952, 23, 779.

[279] T. Yamada, T. Ueda, T. Kitayama, J. Appl. Phys. 1982, 53, 4328.

[280] F. Fang, W. Yang, S. Yu, S. Luo, R. Sun, Appl. Phys. Lett. 2014, 104,132909.

[281] C.-W. Tao, X.-Y. Geng, J. Zhang, R.-X. Wang, Z.-B. Gu, S.-T. Zhang, J.Eur. Ceram. Soc. 2018, 38, 4946.