基于相机阵列的视频稳像方法
魏文力, 黄陆明, 安城辉, 张彩友
(1.国网浙江省电力有限公司检修分公司, 浙江 杭州 311200; 2.国网温州供电公司, 浙江 温州 325000)
视觉传感器由于具有多用途、抗干扰、模块化等优点,正逐渐成为移动通信终端、无人驾驶汽车、无人机等移动装置的重要部件和任务载荷。移动装置采集的视频影像往往存在抖动、晃动和畸变等不稳定因素,这使得依赖视觉信息的控制和相关应用受到极大限制。因此,研究视频稳像技术对于推动通信终端、无人驾驶汽车、无人机的广泛应用具有重大意义。目前,机械稳像方法大多需要在移动装置上搭载相应的机械装置,这就降低了移动装置携带有效载荷的能力。相比之下,电子稳像技术由于无需加载附加的机械配件,正逐渐成为国内外移动装置稳像的主流技术。
1 相关工作
一般来说,电子稳像方法包含三个主要步骤:运动路径估计、运动路径平滑、新视点生成(见图1)。现有的电子稳像技术根据计算原理的不同,主要分为2D[1,2]、3D[3]和2.5D[4,5]三类方法。

图1 视频稳像处理流程Fig.1 Schematic diagram of video stabilization process
2D稳像方法首先估计相邻视频帧之间的二维变换关系,通过连接图像帧之间的变换关系,在2D空间内估计相机运动路径,然后通过平滑2D相机路径实现稳定视频的生成。为了抑制相机低频抖动,Chen等[6]提出用多项式曲线拟合相机的运动轨迹。Gleicher等[7]对相机的运动轨迹进行分段处理,通过对各段轨迹进行独立的平滑计算,获得了更好的稳像效果。最近,Ma等[8]提出一种将轨迹平滑与帧变换融合的视频抖动去除方法。该方法以轨迹平滑为主体,帧变换为辅助,在一阶导数和自适应加权的约束下实现了视频稳像。该研究成果已成功应用于Google公司YouTube网站的视频优化。Liu等[9]仅考虑网格顶点的矢量运动,提出了一种空间平滑稀疏运动场模型的在线视频稳定技术。文献[10]~[12]也是2D方法中的新进展。由于2D类方法只需要估计相邻帧之间的特征匹配,因此鲁棒性较高,运算速度较快。但是,基于特征点匹配的2D方法需要假设场景中的物体位于一个平面内或者相机只进行单纯的旋转运动,因此其应用具有较大的局限性。
3D稳像方法需要估计完备的场景三维结构,即需要以准确的相机3D姿态和场景中点云深度为先验,才能实现稳像。场景三维结构一般可通过SFM算法[13,14]计算获得,或者采用深度传感器直接获取。Buehler等[15]提出一种基于场景摄影重构的三维视频稳像方法,而场景的摄影重构则通过对未标定的相机数据进行SFM计算获得。Zhang等[16]假设场景的欧氏重构已经获得,通过最小化相机在旋转、平移和变焦时的加速度来获取平滑的相机运动轨迹,最终实现视频稳像。Liu等[3]通过引入内容保护规整方法(content-preserving warps,IPW),在合成新视点图像帧的基础上,实现了基于完整三维结构的视频稳像方法。虽然基于3D重构的方法可以获得精度很高的稳像效果,但是由于3D重构本身是一个病态的逆问题,加之采集的视频存在低精度特征匹配、运动模糊、相机快速姿态变化以及焦距变化大等特点,这使得3D重构问题本身就存在精度不高及鲁棒性差的问题。
2.5D稳像方法是介于2D稳像和3D稳像之间的一种折衷方法。2.5D方法认为,完整的3D结构信息对于视频稳像来说是冗余的。因此,它将3D方法中对场景完整结构信息的需求松弛为部分结构信息,并采用对极几何与特征跟踪技术将相机运动信息表达为特征轨迹。Goldstein等[4]利用对极变换方法,在2.5D框架下实现了视频稳像,在一定程度上避免了脆弱的3D重建对稳像的影响。Wang等[17]将每个轨迹表示为贝塞尔曲线,采用时空最优化算法实现了轨迹平滑。Lee等[18]引入特征修剪技术来选择鲁棒的特征轨迹,并在此基础上实现对运动轨迹的平滑。Liu等[3]通过扩展子空间算法来处理立体视频,但该方法的实用性仍受限于场景遮挡和长特征轨迹(超过30帧)的获取。
综上所述,现有方法均能在一定程度上去除视频抖动,但对剧烈抖动、场景存在遮挡等复杂情况均无法获得较好的稳像结果。本文基于多视几何理论,将相机阵列作为视频采集平台,在普吕克坐标系下对相机阵列的运动轨迹进行估计,进而实现视频的稳像。本文的创新在于,提出了一种基于光线匹配的相机阵列运动轨迹估计方法,实现了对复杂场景结构信息的获取,为视频稳像提供了新的研究思路。
2 基于线匹配的相机阵列运动轨迹估计
普吕克坐标系是一个齐次坐标系,与传统的利用笛卡尔坐标系表示直线的方法不同,用普吕克坐标系描述直线可以在不使用无限大的情形下表示射影平面上的任意点[19]。在多视几何中引用普吕克坐标表示光线,可以消除对相机投影中心的依赖性。将相机阵列转换到普吕克坐标系下有两个好处:①在普吕克坐标系中描述光线,投影到均匀光场坐标中的是一个线性映射;② 3D场景中的点可以在相邻时刻的相机阵列中产生线性约束。
根据多视几何理论,相机阵列的运动轨迹由一系列连续的相邻时刻的相对运动组成,如图2所示。其中,Rn、tn分别表示相机阵列从n时刻到n+1时刻的旋转运动和平移运动。X′和X是同一场景点在两个局部相机坐标系中的坐标。由于相机的旋转和平移是相互独立的,因此n时刻的相机路径Cn可拆分为两个部分:相机朝向CRn和相机位置Ctn。因此,相机路径的估计表达式为:
(1)
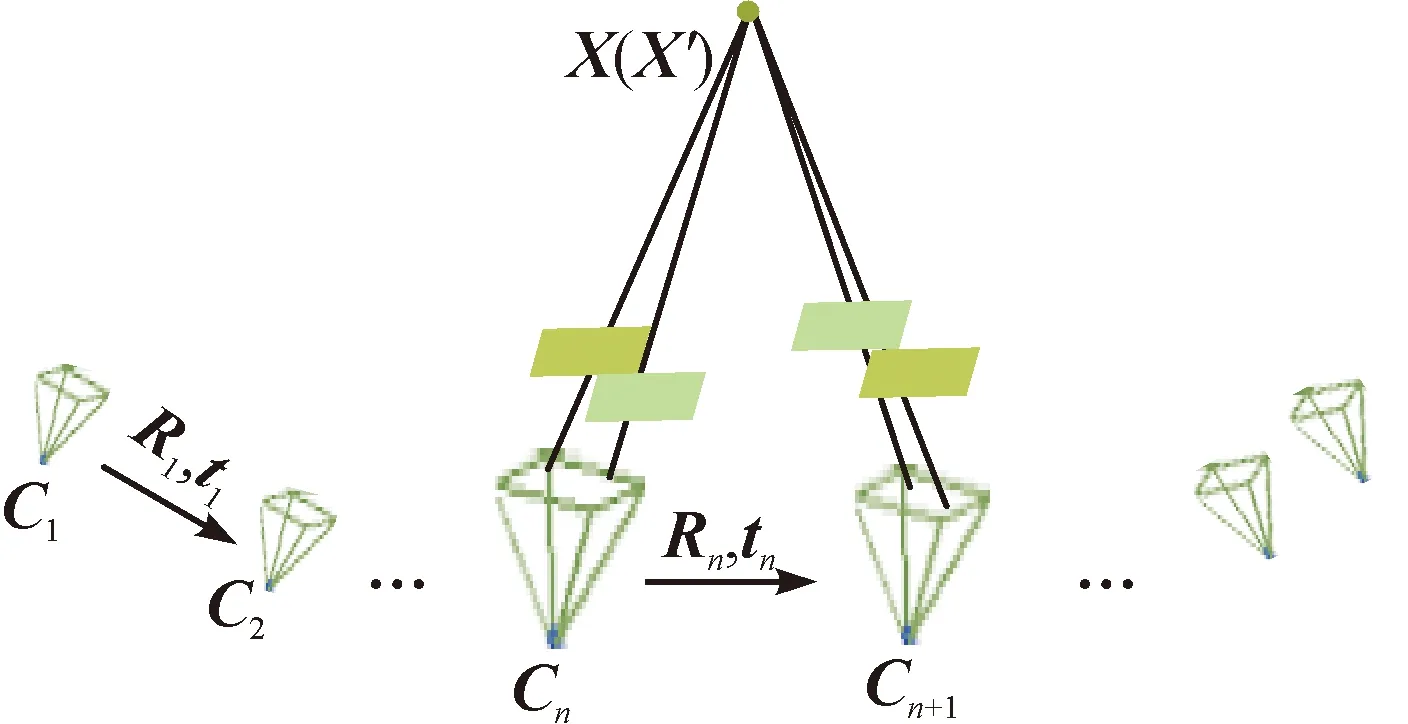
图2 相机阵列的运动轨迹Fig.2 Trajectory of the camera array
以对应空间点的变换关系为基础推导光线之间的线性关系。假设相邻时刻的相机阵列存在旋转矩阵R和平移矩阵t的相对运动,则空间中给定的三维点在相邻帧中的坐标X和X′满足如下关系:
X′=RX+t
(2)
在普吕克坐标系下,空间点(X,X′)之间的关系可用光线对(l,l′)表达,l=(q∶m)和l′=(q′∶m′),其中q表示光线方向,只与旋转矩阵R有关,q′=Rq,m表示直线的矩矢量,同时m=X×q:
(3)
因此,在普吕克坐标系下,光线对的变换关系可写成如下的矩阵形式:
(4)
式中:E=[t]×R是多视几何理论框架下的本质矩阵,是归一化图像坐标下仅依赖于外参的基本矩阵;[·]×表示向量叉积。若n时刻和n+1时刻的相机阵列间存在Rn、tn的相对运动,则n时刻光线集合Ln在n+1时刻的对应光线Ln+1为:
(5)
在普吕克坐标系下,两条光线(q1∶m1)和(q2∶m2)相交可表示为:
(6)
因此根据式(5),可以得到两个相机阵列关于Rn和tn的对极约束关系:
(7)
该约束方程建立了相机阵列之间的基于线匹配的相对运动约束关系。式(7)可改写成线性方程的形式:
AEnvec(En)+ARnvec(Rn)=0
(8)
式中:vec(En)和vec(Rn)分别是En和Rn中所有分量的矢量表达;AEn和ARn是由对应约束集合产生的系数矩阵。
通过变换可消除变量En,得到只含参数Rn的线性方程:
(9)
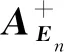
[VD]=eig(MTM)
(10)
式中:eig(·)返回特征值的对角矩阵D和对应的右特征向量为列的矩阵V。
当M是非奇异矩阵时,根据内积的非负性可知MTM是一个正定矩阵,其特征值大于0。构造正定矩阵的正定平方根:
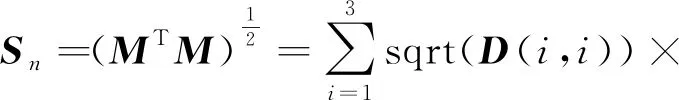
(11)
当M是奇异矩阵时,MTM是一个对称矩阵,其特征值与0的关系不定,特征值按先非0、后0的顺序排列成对角矩阵D。用i表示非0特征值下标,1≤i<3,用j表示0特征值下标,j=i+1,从第j个特征值开始为0。构造对称矩阵的线性根:
(12)
因此,可以用式(13)从M中分解出旋转矩阵Rn。
(13)
其中,±的选择视情况而定,目的是保证M为奇异矩阵时分解得到的旋转矩阵Rn的正交性。为满足‖Rn‖=1约束,对Rn进行归一化操作:
Rn=Rn/det(Rn)
(14)
其中,det(·)用来求矩阵的模值。获得旋转矩阵Rn后,将其代入式(7)得到一个只与平移矩阵tn有关的线性方程,利用最小二乘法可以求解tn。利用上述方法,可以获得所有时刻的旋转矩阵和平移矩阵的线性解,进而获得相机阵列的运动轨迹。
3 本文算法
本文的稳像算法包含三个主要步骤:步骤一是本文提出的复杂场景长轨迹生成方法;步骤二是利用最小曲率变化的路径平滑方法[20]实现平滑路径的生成;步骤三是利用单应矩阵实现新视角视频的生成。
输入:n和n+1时刻相机阵列的视频帧In、In+1;对应的关联光线集合L′n与L′n+1。
输出:从n时刻到n+1时刻相机阵列的稳定视频帧I′n、I′n+1。
步骤一:
1) 从In、In+1中提取关联光线集合L′n和L′n+1,执行式(5)和(7)建立关于Rn、tn的对极约束关系;
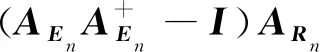
3) 将Rn回代入式(7),得到关于tn的线性方程,利用线性求解方法求出tn的初始解;对于初始解Rn、tn,执行非线性优化操作,获得相机阵列的原始运动轨迹CRn和Ctn。
步骤二:
利用最小曲率变化的路径平滑方法构造能量方程,从CRn和Ctn获取相机阵列在平滑路径上的朝向SRn和位置Stn。
步骤三:
利用3D稀疏点云与2D单应融合的单应矩阵方法,从平滑路径生成新视点视频帧,实现稳像视频I′n、I′n+1的生成。
4 实验与分析
本实验采用Windows 7平台,处理器Intel i7-8700,内存8GB,Visostudio 2013。本文对比算法参考文献[3]的Content-preserving warps(CPW)方法,该算法是3D稳像方法中的代表方法,具有较好的稳像效果。实验数据[16]均由相机阵列获取。cooler 是一个具有显著深度变化的静态场景;juggle 是一个抖动较小的远景动态场景;crowd 是一个具有显著相机抖动的近景动态场景。本文从定性观察有无明显扭曲变形和定量分析稳定视频帧的帧间变换保真度差异(difference of inter-frame transfor- mation fidelity,DITF)两个方面,衡量生成视频帧的质量。帧间变换保真度差异定义为:
DITF(In)=|PSNR(In-1,In)-PSNR(In,In-1)|
(15)
式中:In-1、In、In+1分别表示生成的第n-1、n、n+1帧稳定视频帧;PSNR(In-1,In)为峰值信噪比,用来衡量帧间的相似度。利用峰值信噪比衡量视频的帧间变化,涉及帧间运动和帧间图像变化。当连续两帧间抖动较大或者出现扭曲变形时,帧间变化越大,DITF越高。
图3~图5给出了3种不同场景下本文算法和CPW算法的稳定帧生成结果。

图3 本文算法和CPW算法的稳定帧生成结果对比(cooler)Fig.3 Comparison of the results by the proposed method and the CPW based on cooler

图4 本文算法和CPW算法的稳定帧生成结果对比(crowd)Fig.4 Comparison of the results by the proposed method and the CPW based on crowd
对比黄色和红色框标记的区域可以看出,CPW方法在cooler和crowd场景上均出现了明显的扭曲,分别位于红色框的柱子和黑板区域,原因在于柱子和黑板类似于光滑反光物体,其上的特征点数目较少甚至没有特征点。无特征点的块的单应(即整体2D单应)与周围有特征的块的单应差距较大,各自变换得到的块并不能很好地拼接在一起,因此会出现明显的变形。在juggle场景上,两种算法均没有明显的扭曲变形,但对比图中红色和黄色边框标记的区域可以看出,CPW方法在天花板处有细微的扭曲。此外,CPW算法在图5(a)、(c)上有轻微的凸起,在图5 (b)、(d)上有轻微的凹陷,如图5的第三行所示。出现这种细微扭曲的原因在于,天花板是一个整体平面区域,而CPW算法在分块的过程中并未考虑其整体性,还是对其进行分块操作,使得各块独立按照各自的单应做变换,虽然块与块间的单应相差不大,但仍会导致天花板处块与块不能完美地拼接成一个平面,从而出现这种扭曲。这种扭曲在单个视频帧上不易被肉眼察觉,但在动态的视频中会造成严重的视觉影响。

图5 本文算法和CPW算法的稳定帧生成结果对比(juggle)Fig.5 Comparison of the results by the proposed method and the CPW based on juggle
除了上述定性分析,本文还利用帧间变换保真度差异(DITF)对两种算法生成的稳定视频进行定量分析,如表1所示。
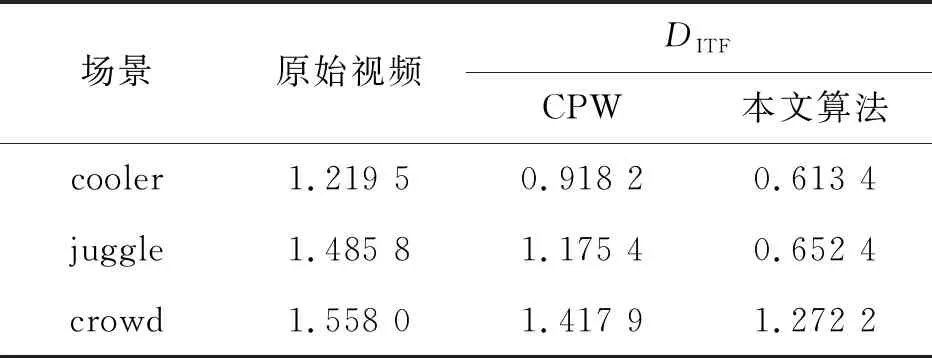
表1 两种算法的平均帧间保真度差异(DITF)Tab.1 DITF of the two algorithms
可以看出对于3个场景,本文算法和CPW算法的DITF相对原始视频均有所降低,但本文算法的DITF均比CPW低,这表明本文算法生成的稳定视频的帧间变换较小、稳定度较高,说明本文算法效果更好。
最后,比较本文算法和CPW算法生成视频帧所用的时间。表2给出了两种算法在3个场景上平均每帧的生成时间。

表2 两种算法的稳定视频帧生成时间对比Tab.2 Comparison of video frame generation time between two algorithms
由表2可以看出,本文算法比CPW算法快了8~9倍,且平均每帧的生成时间约为0.1 s,基本可以达到实时效果。
实验结果表明,本文提出的基于线约束的稳像方法,无论是视觉效果还是量化的保真度差异,都优于对比算法,同时,本文算法的计算效率也明显优于对比算法。
5 结 语
本文以相机阵列作为数据采集平台,实现了基于光线匹配的相机阵列路径生成,并在此基础上使用基于最小曲率变化的路径平滑方法和基于单应矩阵的稳定视频帧生成方法,实现了快速高效的视频稳像。相较于传统的基于单目视觉的方法,本文方法对于视频剧烈抖动、场景存在遮挡等复杂情况均能获得较好的稳像结果。后期研究会将相机阵列用于视频模糊的去除,从而提升稳像视频的质量。本文所提方法在电力行业的多传感器无人机巡检、搭载多相机的移动消费终端视频质量提升以及基于相机阵列的相关视觉应用等领域具有广阔的应用前景。未来还需在系统轻量化、降低能耗和成本方面持续优化。

