Neutrosophic κ-Structures in Ordered Semigroups

G.Muhiuddin,K.Porselvi,B.Elavarasan and D.Al-Kadi

1Department of Mathematics,Faculty of Science,University of Tabuk,Tabuk,71491,Saudi Arabia

2Department of Mathematics,Karunya Institute of Technology and Sciences,Coimbatore,641114,India

3Department of Mathematics and Statistic,College of Science,Taif University,Taif,21944,Saudi Arabia

ABSTRACT In general,ordered algebraic structures,particularly ordered semigroups,play an important role in fuzzification in many applied areas,such as computer science,formal languages,coding theory,error correction,etc.Nowadays,the concept of ambiguity is important in dealing with a variety of issues related to engineering modeling problems,network theory,decision-making problems in real-life situations,and so on.Several theories have been developed by various researchers to overcome the difficulties that arise from uncertainty,including fuzzy sets,intuitionistic fuzzy sets,probability,softsets,neutrosophic sets,and many more.In this paper,we focus solely on neutrosophic set theory.In ordered semigroups,we define and investigate the properties of neutrosophic κ-ideals and neutrosophic κ-interior ideals.We also use neutrosophic κ-ideals and neutrosophic κ-interior ideals to characterize ordered semigroups.

KEYWORDS Ordered semigroup;ideals;neutrosophic κ-structures;neutrosophic κ-ideals;neutrosophic κ-interior ideals

1 Introduction

In[1],Zadeh proposed the theory of fuzzy sets to model vague notions in the universe.In[2],Atanassov generalized the fuzzy set theory concepts and renamed as Intuitionistic fuzzy set theory.According to his view,there are the two kinds of degrees of freedom in a globe such as membership to a vague subset and non-membership to that given subset.In[3],Rosenfeld introduced the concepts of fuzziness in groups and obtained several results.Recently,many researchers pursue their research in this area and these concepts have been applied to different algebraic structures such as semigroups,ordered semigroups,rings(see[4–10]).

Smarandache proposed the notions of neutrosophic sets to handle uncertainty that arises everywhere.It is the generalization of fuzzy sets and intuitionistic fuzzy sets.Using these three attributes such as a truth(T),an indeterminacy(I)and a falsity(F)membership functions,neutrosophic sets are characterized.These sets have numerous applications in various disciplines to deal with the complexities that arise primarily from ambiguity data.A neutrosophic set can differentiate between relative and absolute membership functions.Smarandache used these sets in non-standard analysis,namely decision making theory,control theory,decision of sports(winning/defeating/tie),etc.

In[11],Muhiuddin et al.presented the notion of implicative neutrosophic quadruple-algebras,and various properties were investigated.In[12],Muhiuddin et al.found the relationship between(ε,ε)-neutrosophic ideal and(ε,ε)-neutrosophic subalgebra in a BCK-algebra.Also,they provided conditions under which an(ε,ε)-neutrosophic subalgebraic structure to be an(ε,ε)-neutrosophic ideal structure.In[13],Muhiuddin et al.introduced the theory of neutrosophic implicative κ-ideal in BCK-algebras,and examined its properties.In addition,the relationship between different kinds of neutrosophic implicative κ-ideals were discussed.

In[14],Khan et al.defined and discussed various properties of neutrosophic κ-subsemigroup andε-neutrosophic κ-subsemigroup in a semigroup.As a motivation from[14],we delve into different types of notions of neutrosophic κ-structures,namely neutrosophic κ-ideals,neutrosophic κ-bi-ideals,neutrosophic κ-interior ideals and investigated various properties.In[15],Elavarasan et al.proposed the notions of neutrosophic κ-ideals and characteristic neutrosophic κ-structure in semigroup and discussed its properties.Further,the equivalent assertions for characteristic neutrosophic κ-structure were provided.In[16],Porselvi et al.defined and obtained various properties of neutrosophic κ-bi-ideal structure in a semigroup.We have shown that both neutrosophic κbi-ideals and neutrosophic κ-right ideals were the same if the semigroup is regular left duo.Moreover,we have obtained equivalent conditions for regular semigroup in terms of neutrosophic κ-product.In[17],Porselvi et al.defined and discussed the notions of neutrosophic κ-interior ideal structures and neutrosophic κ-simple in semigroup.Also,we explored equivalent assertions for a simple semigroup,and neutrosophic κ-interior ideal structures.For more concepts related to this work,we refer the readers to[18–23].

The aim of this paper is to define the concepts of neutrosophic κ-ideals,neutrosophic κbi-ideals and neutrosophic κ-interior ideals in ordered semigroup,and discuss its properties.We obtain an equivalent assertion of an interior ideal in ordered semigroup in terms of characteristic neutrosophic κ-structures.Further,we define the notion ofε-neutrosophic κ-ideals andε-neutrosophic κ-interior ideals in ordered semigroup,and explore its properties.Moreover we show that the preimage of neutrosophic κ-right(resp.,left,ideal)ideal is neutrosophic κ-right(resp.,left,ideal)ideal under a homomorphism of an ordered semigroup.

2 Preliminaries

It is evident that all the neutrosophic κ-ideals are neutrosophic κ-bi-ideals,but neutrosophic κ-bi-ideal need not be a neutrosophic κ-ideal,as given by an example.

Example 2.1.Consider the ordered semigroup N:={k1,k2,k3,k4,k5}with the binary operation“.” and the partial order “≤” as follows:

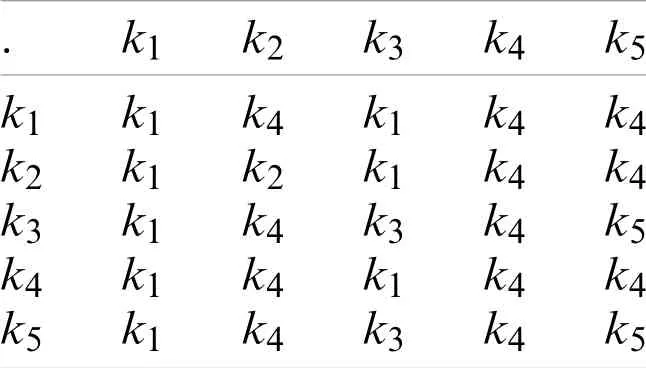
.k1k2k3k4k5 k1k1k4k1k4k4 k2k1k2k1k4k4 k3k1k4k3k4k5 k4k1k4k1k4k4 k5k1k4k3k4k5

and ≤:={(k1,k1),(k1,k3),(k1,k4),(k1,k5),(k2,k2),(k2,k4),(k2,k5),(k3,k3),(k3,k5),(k4,k4),(k4,k5),(k5,k5)}.

3 Neutrosophic κ-Structures in Ordered Semigroups

4 Conclusion

In ordered semigroups,the concepts of neutrosophic κ-ideals,neutrosophic κ-bi-ideals,and neutrosophic κ-interior ideals were introduced and their properties were investigated.We defined ordered semigroups by employing various neutrosophic κ-ideals,neutrosophic κ-bi-ideals,neutrosophic κ-interior ideals and so on.In our future work,we intend to define different types of notions in neutrosophic κ-structures over-ordered semigroups,such as neutrosophic κ-prime,neutrosophic κ-quasi-prime,and investigate the structural properties of ordered semigroups using the concepts and results in ordered semigroups.Hopefully,our research work will continue in this direction and will create a platform for other algebraic structures.

Funding Statement:The authors are grateful to the anonymous referees for careful checking of the details and for helpful comments that improved this paper.This work was supported by the Taif University Researchers Supporting Project(TURSP-2020/246),Taif University,Taif,Saudi Arabia.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.