Isogeometric Analysis with Local Adaptivity for Vibration of KirchhoffPlate

Peng Yu,Weijing Yun,Junlei Tang and Sheng He

College of Civil Engineering and Architecture,Key Laboratory of Disaster Prevention and Structural Safety of Ministry of Education,Guangxi Key Laboratory of Disaster Prevention and Structural Safety,Guangxi University,Nanning,530000,China

ABSTRACT Based on our proposed adaptivity strategy for the vibration of Reissner–Mindlin plate,we develop it to apply for the vibration of Kirchhoffplate.The adaptive algorithm is based on the Geometry-Independent Field approximaTion(GIFT),generalized from Iso-Geometric Analysis(IGA),and it can characterize the geometry of the structure with NURBS(Non-Uniform Rational B-Splines),and independently apply PHT-splines(Polynomial splines over Hierarchical T-meshes)to achieve local refinement in the solution field.The MAC(Modal Assurance Criterion)is improved to locate unique,as well as multiple,modal correspondence between different meshes,in order to deal with error estimation.Local adaptivity is carried out by sweeping modes from low to high frequency.Numerical examples show that a proper choice of the spline space in solution field(with GIFT)can deliver better accuracy than using NURBS solution field.In addition,for vibration of heterogeneous Kirchhoffplates,our proposed method indicates that the adaptive local h-refinement achieves a better solution accuracy than the uniform h-refinement.

KEYWORDS Isogeometric analysis;local refinement;adaptivity;vibration;kirchhoffplate

1 Introduction

Isogeometric analysis(IGA)was proposed in[1]to assemble analysis in Computer Aided Engineering(CAE)and Computer Aided Design(CAD).Due to high continuity of NURBS basic functions[1,2],NURBS-based IGA is widely used in the field of engineering structure,such as shape optimization of structure[3–5],vibration of plates,including Kirchoff plate[6–9]and Reissner–Mindlin plate[10–13].These studies have shown that IGA results are often better than traditional finite element method(FEM)based approaches.Since ford≥2,NURBS are defined with tensor product form,the refinement is constrained by the global structured grid(see Fig.1a).Unfortunately,this leads to extra computational costs as the mesh is refined for the solution field.Moreover,the tensor product based refinement does not facilitate local refinement to capture local phenomenon,e.g.,sharp gradients or boundary layer.

Figure 1:(a)NURBS global refinement and(b)expected local refinement

To address this problem,two approaches have been used in the literature.In[14],authors consider NURBS local prolongation operators which are based on multigrid principles.However,this approach needs to construct an operator by marking some extra elements for refinement,thereby,the resulting adaptive mesh is not the most efficient one.This situation can be partially alleviated by the use of hierarchical refinements of NURBS[15].Another approach is to use splines with local refinement properties[14–19].In authors’opinion,the most commonly used splines with local refinement possibility are(truncated)hierarchical B-splines[20–23],T-splines[16,17],and PHT-splines(polynomial splines over hierarchical T-meshes)[18].Because of a convenient local cross insertion and removal algorithm,we use PHT-splines in this study.PHT-splines have been used to solve static elastic solid issues.Numerical results show that the adaptive PHT refinement enjoys a higher convergence rate than uniform NURBS refinement[24].However,since PHTsplines are polynomial functions,they are not able to exactly represent the geometry of shapes with conic sections,e.g.,circles,ellipsoids,and spheres,which typically arise in engineering design and analysis.To tackle with this limitation,rational splines over hierarchical T-meshes(RHTsplines)have been recently introduced in[25].Nevertheless,the continuity of RHT-splines is limited to onlyC1.Though the continuity ofC1is sufficient for the analysis of many engineering problems,for the description of geometry requiring higher continuity,RHT-splines will suffer from the geometry inexactness.To weaker this tight coupling between geometry and simulation,a new approach called Geometry-Independent Field approximaTion(GIFT)has been proposed[26].This approach utilizes spline spaces for solution field independently of that for the geometry representation,and thus,offers the advantages of both the worlds.For instance,NURBS is used for the geometry representation(taken directly from the CAD model),and PHT-splines are use for the solution field.Thereby,the geometry information is preserved,and the local refinement is(independently)performed only on solution field.There are three main contributions of this article.(1)The GIFT method is employed to investigate the structural vibration based on the Kirchhoff plate theory.(2)In case of vibration,the advantage of GIFT is demonstrated with a feasible selection of spline domain of physical field.(3)Based on our established adaptive method for the vibration of thick plate problem[27],we extend to the adaptivity for thin plate vibration by sweeping the mode driven by a-posteriori error estimation,with the help of MAC method to recognize the correspondence between two different mesh spaces.

The organization of this paper is as follows.In Section 2,the variational form of linear elasto-dynamics,based on Kirchhoff plate theory,is set up.The weak form,based on IGA and GIFT framework,is introduced in Section 3.In Section 4,a-posteriori error estimation and the hierarchical local refinement process is developed.In Section 5,the a-posteriori error estimates and hierarchical local refinement of proposed in Section 4 is combined with MAC for modal analysis,and the resulting error-driven local adaptivity for vibration is presented.In Section 6,several numerical examples are presented.These results using GIFT approach show two major achievements:(1)Despite a poor geometric parameterization,an accurate numerical approximation can be obtained by adopting an appropriate parameterization in solution field.(2)When structural vibration is localized,the proposed adaptive refinement delivers a better convergence rate than the uniform refinement.

2 Problem Statement

LetΩ⊂Rdrepresent the spatial domain of an elastic plate,and let(x,y,z)denote the Cartesian coordinate system.Moreover,let(u,v,w)denote the deflections of the plate in the(x,y,z)directions,respectively,andhdenote the thickness of the plate in thezdirection.Based on the Kirchhoff plate theory,see e.g.,[28],the displacement componentsuandv,at a distancezfrom the neutral surface,can be expressed as

wherewis the deflection of the neutral plane of the plate in thez-direction.Thereby,wis the only independent variable,and we obtain a simple relationship

Moreover,the relationship between the three components of strain and the deflection is given by

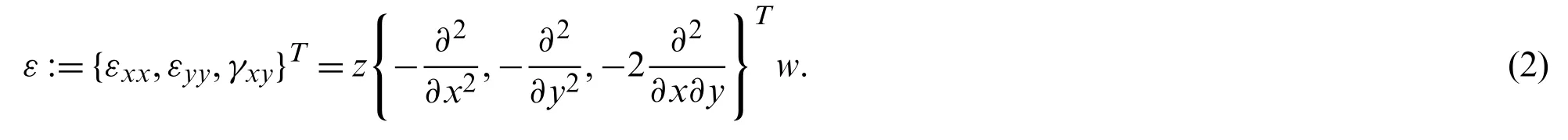
By introducing the differential matrices

the relations(1)and(2)can be written as

LetCbe the matrix of material stiffness constants.The in-plane(normal and shear)stressesσxx,σyy,andσxycan then be obtained,by substituting the value ofεinto the constitutive relationσ=Cε,as follows:

To evaluate the strain at the neutral plane of the plate,hence independent of the coordinatez,we introduce thepseudostrain εp,which is defined as

Let the parameterD=Eh312(1 -ν2)denote the bending stiffness of the plate,whereEis the Young’s modulus,andνis the Poisson’s ratio.Furthermore,letMxx,Myy,andMxydenote the bending moments,and twisting moments,respectively,which are defined as

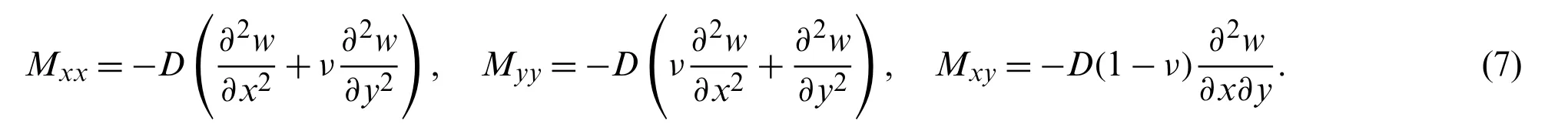
These three components of the moments then define thepseudostressas

LetDdenote the constant matrix of the material property and the plate thickness,which is defined as

For a thin plate,the generalized Hooke’s law then gives the relation ofpseudostressandpseudostrainas

Now letVxzandVyzdenote the shear forces.Considering the moment equilibrium of the plate cell with respect to thex-(andy-)axis,and neglecting the second order small terms,leads to a relation in terms of moments

Letρdenote the mass density of the plate material.The plate cell is then subjected to the inertial forceρh¨w.In deriving the system equilibrium equations,now consider the equilibrium of the small plate cell in thezdirection,which can be written as

dVxzdy+dVyzdx+(bz-ρh¨w)dxdy=0,

wherebzis the external force.Usingd Vxz=∂Vxz∂x dx,andd Vyz=∂Vyz∂y dy,we get

Substituting the relations of shear forces from(11),and the moments from(7),we get the following equation for homogeneous and isotropic plates

For free vibration analysis,withbz=0,we get

We consider the clamped boundary conditions on all side,i.e.,

We now introduce the function spaceV0={v∈H2(ω):v=∂v∂n=0 onγ}.Then the elasto-dynamic vibration problem in variational form reads[7,28]

whereuis the displacement field,is the virtual displacement,andis the virtual strain.Then,using the relation of pseudostress and pseudostrain(10),the weak form(15)can be rewritten as

3 The Discrete Form Using GIFT

LetPbe the parametric domain.The physical domainωis parametrized onPby a geometrical mappingF

We assume that the domainωmay consist sub-domains such thatTypically,the geometrical mapFis given by a set of basis functionsNi1,i2,...,id(ε)and a set of control pointsP i1,i2,...,idas

whereNi1,i2,...,id(ε)can be ad-dimensional tensor product of NURBS,B-splines,T-splines,PHT-splines,etc.For brevity reasons,we introduce two sets of multi-indices(i1,i2,...,id)of NURBS basis functions by

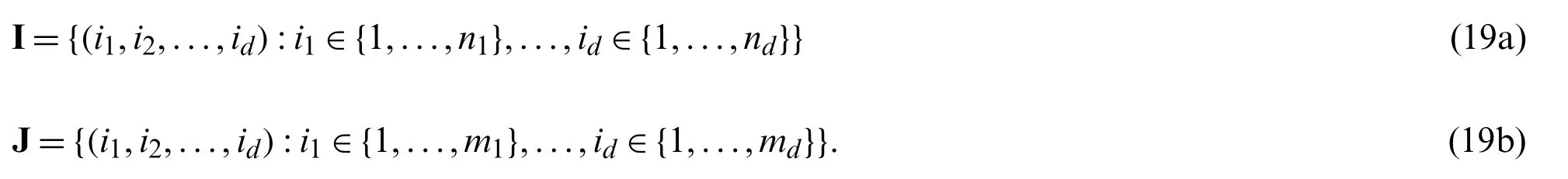
Moreover,wherever suitable,for multi-index(i1,i2,...,id)we will interchangeably use the collapsed notationkThence,Eqs.(17)and(18)are written as

In what follows,we will refer to the set {Nk()}k∈Ias thegeometry basis.For change of variables,we will also need the Jacobian matrixJ(ε)of the mappingF,which is given by

The GIFT method is presented in detail by Atroshchenko et al.[26].In IGA,the solution fielduIis represented through the same spline functions which are used for the geometry

Now,using the basis functionsMk( ),we approximate the deflectionwin Eq.(16)as

whereMk(ε)are basis functions,andwkare unknown control variables.Substituting(25)in(16),we obtain the discrete form of the dynamical equation as follows:

wherewdenotes the vector of deflections at the control points,andKandMrespectively denote the stiffness and mass matrices,which are defined as follows

whereMxdenotes the basis functions from the spaceVG,and the matrixmthe mass matrix

The general solution of the free vibration Eq.(26)can be expressed as

whereiis the imaginary unit,is the eigenvector,andλis the natural frequency.Substituting(29)into(26),and ignoring the virtual quantity,the natural frequencyλof thin plates can be calculated by solving the following generalized eigenproblem:

3.1 Boundary Conditions

As eigenproblem(30)does not include the essential boundary conditions,it is necessary to find a proper way to impose essential boundary conditions.Some of the methods proposed in the literature to impose essential boundary conditions,e.g.,[29,30]can be extended to the isogeometric framework.However,for efficiency reasons,we prefer another approach[31].

In this approach,simply supported boundary condition can be imposed through fixing thez-component of the first row of control variables for the respective boundary.Clamped boundary conditions can be imposed by fixing thez-component of the first two rows of control variables for the respective boundary.

In the next section,we introduce the error in the energy norm,and then define the hierarchical local refinement process.Unless otherwise stated,in what follows,we only compute the energy norm of the variables.

4 Hierarchical Local Refinement

For the complex cases,it is difficult to obtain the analytical solution for generalized eigenproblem(30).Therefore,to compute the errors in our numerical solution,we compute the solution on a refined mesh.This mesh is called therefined mesh,and the solution on it is called thebetter solution.Let ¯u denote the better solution,andu hdenote the numerical solution at a mesh with characteristic mesh sizeh.Then,the error in the numerical solution can be written as e=¯u-uh.Note that the refined mesh elements are created by dividing each element of the current mesh intoNe=2d·Leelements,wheredis the dimension of the problem,andLeis the level of refinement,which is set by the user.The element-wise error in the energy norm for theith elementis then defined as

Now LetNdenote the total number of elements in the domain.Then,the energy norm of error in the whole domain is defined as

Letηdenote the error tolerance,i.e.,if the error in any element is above this threshold,then the element is marked for refinement.For element marking,we employ the mean-value strategy with some simple modification.To be specific,we first select the elements for which the error satisfieswhereτis certain percentage(chosen as 20% in this article).Let us assume that the number of such selected elements be ¯N.Out of these elements,let the number of elements

Thence,we mark the elements whereand refine them intoNeelements.The process of adaptive local refinement has been summarized in Algorithm 1.For the 2D case,withLe=1,the adaptive process of Algorithm 1 is presented in Fig.2.

Algorithm 1:Adaptive hierarchical local refinement strategy Input:solution uh and u Output:Mesh domain ω after adaptivity 1.Compute the error e=u-uh 2.Loop over elements i===1,2...N in current mesh domain Ω(a)Compute the local error indicator ‖e‖2Ωei(b)if ‖e‖2Ωei ＞η,mark element i to be refined 3.End loop over elements 4.Refine marked elements in current mesh domain Ω to generate a new finer mesh Ω*5.Replace Ω with Ω*

5 Error-Driven Local Adaptivity for Vibration

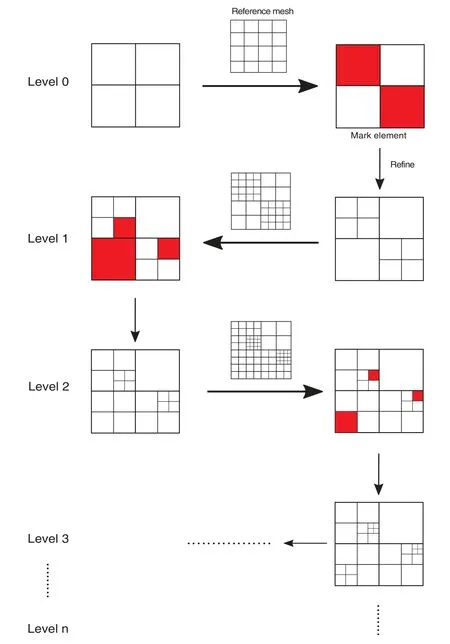
Figure 2:Adaptive refinement process of Algorithm 1 in 2D

5.1 Modal Assurance Criterion

Modal Assurance Criterion(MAC)is a statistical indicator originally proposed for orthogonality check[32]and has been developed as one of the most well-known method to compare modal vectors quantitatively[33].In this paper,it is utilized for assistance for error estimation between two different mesh systems.The value of MAC is computed as the scalar product of the two sets of normalized eigenvectorsandwherethe is eigenvector at themode in the refined mesh,andis the eigenvector at theithmode in current mesh.Note that,unless otherwise stated,the eigenvectors are normalized.The outcome will be assembled into MAC matrixusing the formula

where ||·||mis the mass norm and defined by

andmis the mass matrix defined in Eq.(28).The values of the MAC matrix are located in the interval[0,1],where 0 means no consistent resemblance whereas 1 means a consistent correspondence.Generally,it is accepted that large values denote relatively consistent correlation whilst smaller value represents poor association of the two modal vectors.For instance,an example of MAC matrixare illustrated in Table 1 with 3D view in Fig.3a.For the first three modes,it is obvious thatare correlated torespectively but orthogonal to those in rest modes.However,when it comes to the 4th and 5th modes,we can see the resemblance are not unique any more.Instead,it is exhibited as a block made up with 4 bars marked with red circle in Fig.3a.That is because 4th and 5th modes in both current and refined domains are multiple modes thatandseparately represent one pair of basis for eigenvector space for current and refined mesh.The method to tackle with the multiple modes is introduced in our work[27],and after the measurement,it can be seen that the block of MAC matrix shown in red circle in Fig.3a are merged into a bar in red circle in Fig.3b,namely,Accordingly,the conversion is also made in Table 2.MAC helps to construct correlation of modal vectors between current and refined domain.Combined with scheme of error estimation and hierarchical refinement proposed in Algorithm 1,strategy of adaptive local refinement for vibration would be developed in the following section.

Table 1:An example of MAC matrix with multiple eigenvectors(in highlights)before projection.Row number is for mode and column number is for i mode

Table 1:An example of MAC matrix with multiple eigenvectors(in highlights)before projection.Row number is for mode and column number is for i mode

Mode12345...1 0.99270.00000.00000.00000.0000...2 0.00000.97700.00000.00000.0000...3 0.00000.00280.98930.00000.0000...4 0.00000.00000.00000.45930.4263...

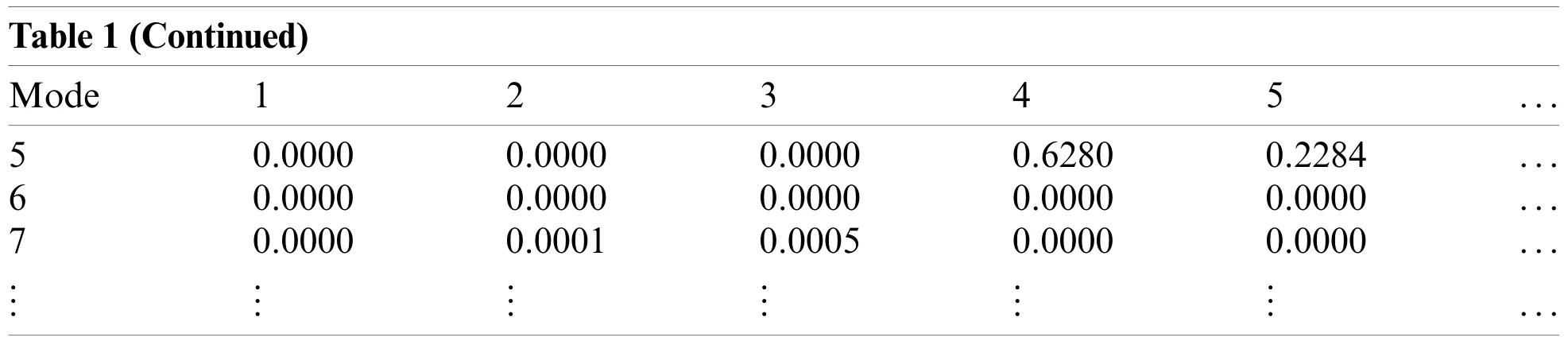
Table 1(Continued)Mode12345...5 0.00000.00000.00000.62800.2284...6 0.00000.00000.00000.00000.0000...7 0.00000.00010.00050.00000.0000........................

Table 2:An example of MAC matrix M after projection of multiple eigenvectors(in box).Row number is for mode and column number for i mode

Table 2:An example of MAC matrix M after projection of multiple eigenvectors(in box).Row number is for mode and column number for i mode

Mode 1234–5...1 0.99270.00000.00000.0000...2 0.00000.97700.00000.0000...3 0.00000.00280.98930.0000...4–50.00000.00000.00000.8702...6 0.00000.00000.00000.0000...7 0.00000.00010.00050.0000...

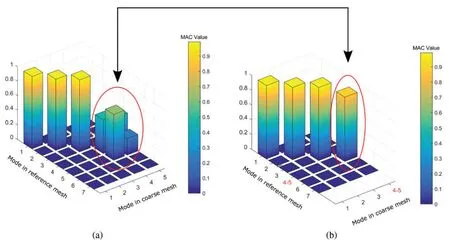
Figure 3:An example of 3D view for MAC values.(a)MAC matrix with multiple eigenvectors(in red circle)before projection;(b)MAC matrix after projection of multiple eigenvectors(in red circle)

5.2 Adaptive Local Refinement for Vibration

As we know,mode shapes of structural vibration are often different from modes to modes.One may pay attention to the mode shapes around specific range of frequency according to engineering problems.For general applications,in this paper,the adaptive refinement is carried out via sweeping modes from low to high frequency.The procedure is summarized in Algorithm 2.

Algorithm 2:Adaptivity by sweeping modes for vibration for i ←1 to n modes in current mesh do for i ←1 n modes in refined mesh Compute do Compute Mi,i and Mi+1,i.if ηminM ＜[Mi,i,Mi+1,i]＜ηmaxM and |λi+1-λi|/λi ＜ηλthen Identify(i,i+1) modes and(i,i+ 1)modes are correlated double eigenmodes.Call the algorithm[27]to deal with the multi-eigenmodes to obtain equivalent φhi,φi.else Identify i mode is an unique mode.end Pick up Mmaxi,i=Max{M1,i,...,Mn,i}and mark i.Compute eλi and eφ i with(i,i).if Mmaxi,i ＞¯ηM or eλi ＞ηλ or eφ i ＞ηφ then Call Algorithm 4(Let uh=φhi,u=φi).else Move to mode i + 1 or i + 2(multiple modes).end end end In this paper,we set tolerannce that ηminM=0.05,ηmaxM=0.9,¯ηM=0.95,ηλ=0.1%,ηφ=0.5%.

6 Numerical Tests

Four numerical examples are carried out for the following purposes.Example in Section 6.1 is the vibration investigation of circular plate to show that GIFT method has the merit of flexibility to choose spline space in solution field independently from that of geometry,which would yield better solution compared to IGA on condition that control points describing geometry are distributed unreasonably.Examples in Sections 6.2–6.4 employ GIFT,with NURBS representing geometry and PHT describing solution field,to study vibration problem for heterogeneous plate with different shapes,especially,analysis of multiple modes is presented in example in Section 6.2.These heterogeneous plate perform obvious concentrated local response where PHT is able to show the advantage of local refinement.Noted that in instances of Sections 6.2–6.4,due to lack of theoretical solution for the problems,we adopt the computational result from the very fine uniform mesh as the approximation of analytical solution.

6.1 Circular Plate

The geometric and material parameters for circular plate are listed in Table 3,with radiusR,thicknessh,Young’s modulusE,and densityρ.On assumption that the geometry of circular plate is established by cubic NURBS basis functions with irregularly distributed control points 24 × 24,shown in Fig.4a.In IGA scheme,the solution space in Fig.4b is imposed to be the same as geometric space.However,GIFT is free to pick up the solution space so that the uniform one in Fig.4c is preferred here.For better comparing with theoretical results[34],the normalized natural frequency related parameteris defined

Table 3:Geometric and material constants for circular plate

whereλis natural frequency andDis flexural stiffness.Consequently,supposed thatis computational natural frequency related parameter,the relative erroreNcan be written as

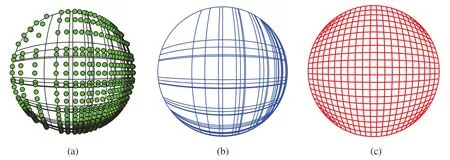
Figure 4:The same geometry parameterization and different spline spaces in solution field of IGA and GIFT for circular plate.Cubic NURBS for both IGA and GIFT.(a)Geometry with 24 ×24 control points;(b)Geometry with 24 × 24 control points;(c)Geometry with 24 × 24 control points

In this example,IGA and GIFT method is compared with exact solution in simply supported boundary condition and clamped boundary condition separately,where the difference of these two boundary conditions has been clarified in Section 3.1.The results are illustrated in Tables 4,5 and Fig.5.It is observed that GIFT shows a better accuracy than IGA with increasing of modes.This example inspires us that when the geometric space of structure is not good enough,we can count on GIFT to re-construct the solution space to achieve a better precision.

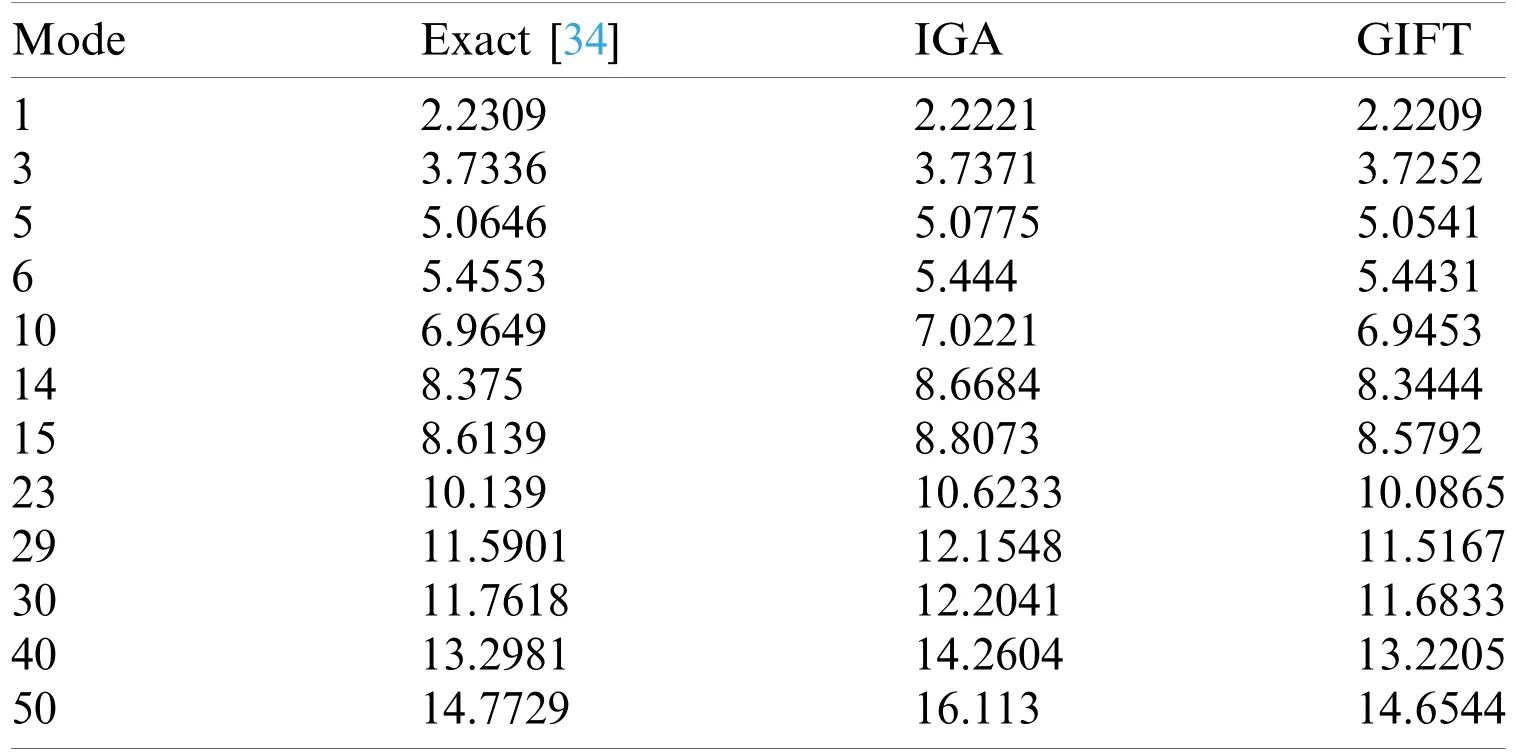
Table 4:Comparison of eN for simply supported circular plate

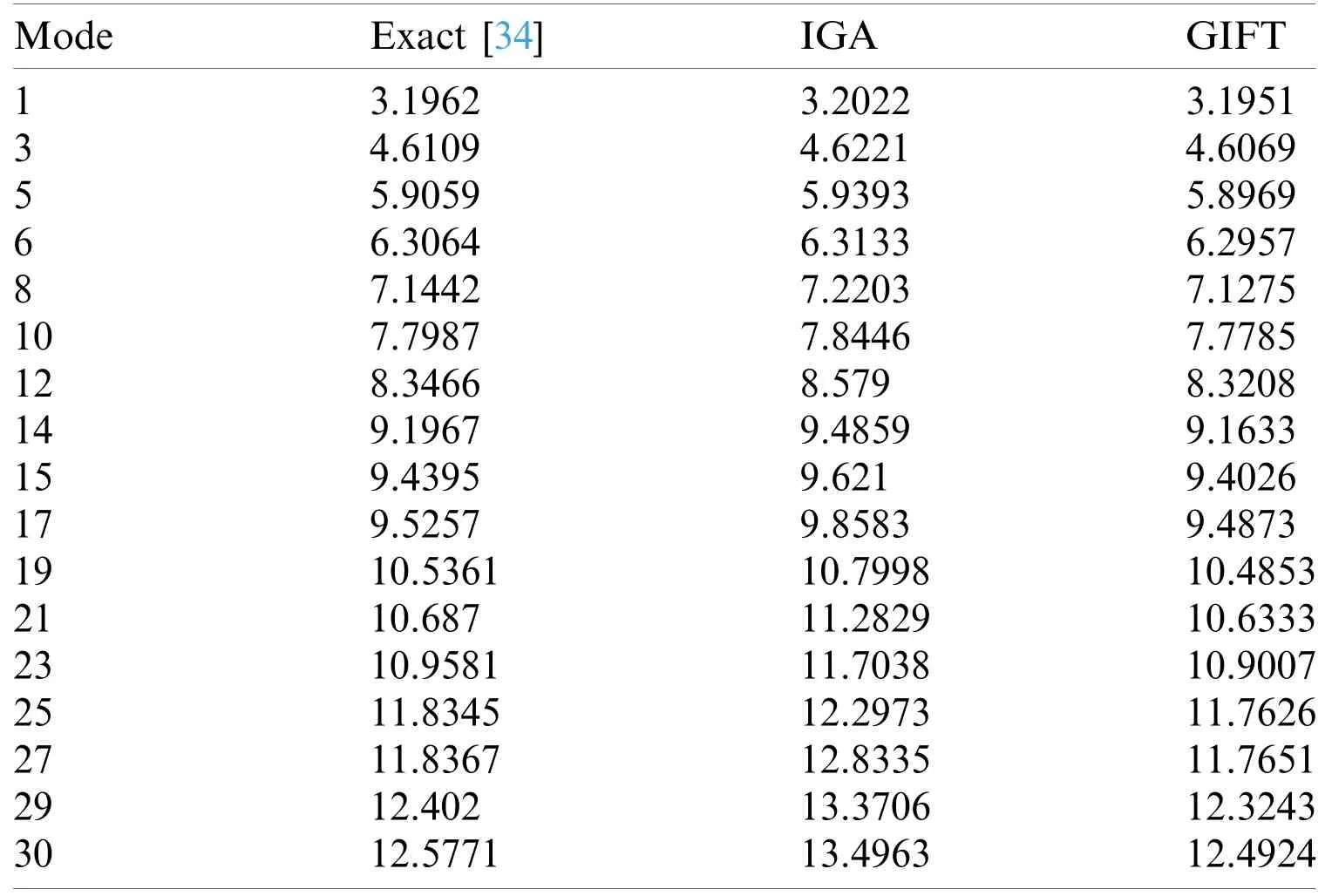
Table 5:Comparison of eN for clamped circular plate

Figure 5:Comparison of eN between IGA(729 control points)and GIFT(576 control points)in solution field(Cubic NURBS,cpts control points).(a)Simply support;(b)clamped

6.2 Heterogeneous L-Shape Plate

In this test,a heterogeneous L-shape structure is built with 3 Patches where relevant geometric parameters and material constants are displayed in Fig.6a.The whole domain boundary is simply supported.Densityρis 2700,and thicknesshis 0.01 and Poisson’s rateνis 0.3.The Young’s modulus of 3 Patches isE2=E=107,E1=E3=1000E2respectively so that it is evident the vibration would be concentrated in the Patch 2 as the material is softest in this area.As explicitly discussed on the principle in Section 5,the adaptivity starts with an initial mesh in Fig.7a from the 1th mode and afterwards sweeps from low to high frequency.Here we would like to emphasize that firstly,the error indicators of both natural frequencyand eigenvectorat 1th are compared in the situation that the refined mesh is generated with refinement levelLe=1,2,3,respectively.Seen from Figs.9a and 10a,the three plots perform the almost same convergence rate,which symbolizes the refinement levelLe=1 we select for error estimation is reasonable.In addition,the adaptive performance in different modes is able to be fairly understood from Figs.7,9b and 10b.Particularly,from Fig.9b,we can see the local refinement is conducted at 1th,2–3th,5–6th,9–10th modes.While there is no refinement for 4th,7–8th,11th,12–13th,14–15th since the solutions by mesh state which they inherit from the previous modes are underneath the error indicator,namely,it does not meet the condition at Step(h)in Algorithm 5.2 and then move to Step(i).Similarly,this state can be also observed in Fig.7 that 2–3th mode share the mesh with 4th mode,and 5–6th mode share the mesh with 7–8th mode,etc.Furthermore,it is noted that in some situation thatin Fig.9b,though,it still has to be refined.That is because conditionis unsatisfied.Obviously,from Figs.9b and 10b,compared with,the decrease ofis more tough to achieve.Besides,the contrast of relative error in energy norm is made between adaptive refinementeadpand uniform refinementeuni,where the errors are calculated by comparing to the approximation of exact solution ˆu that

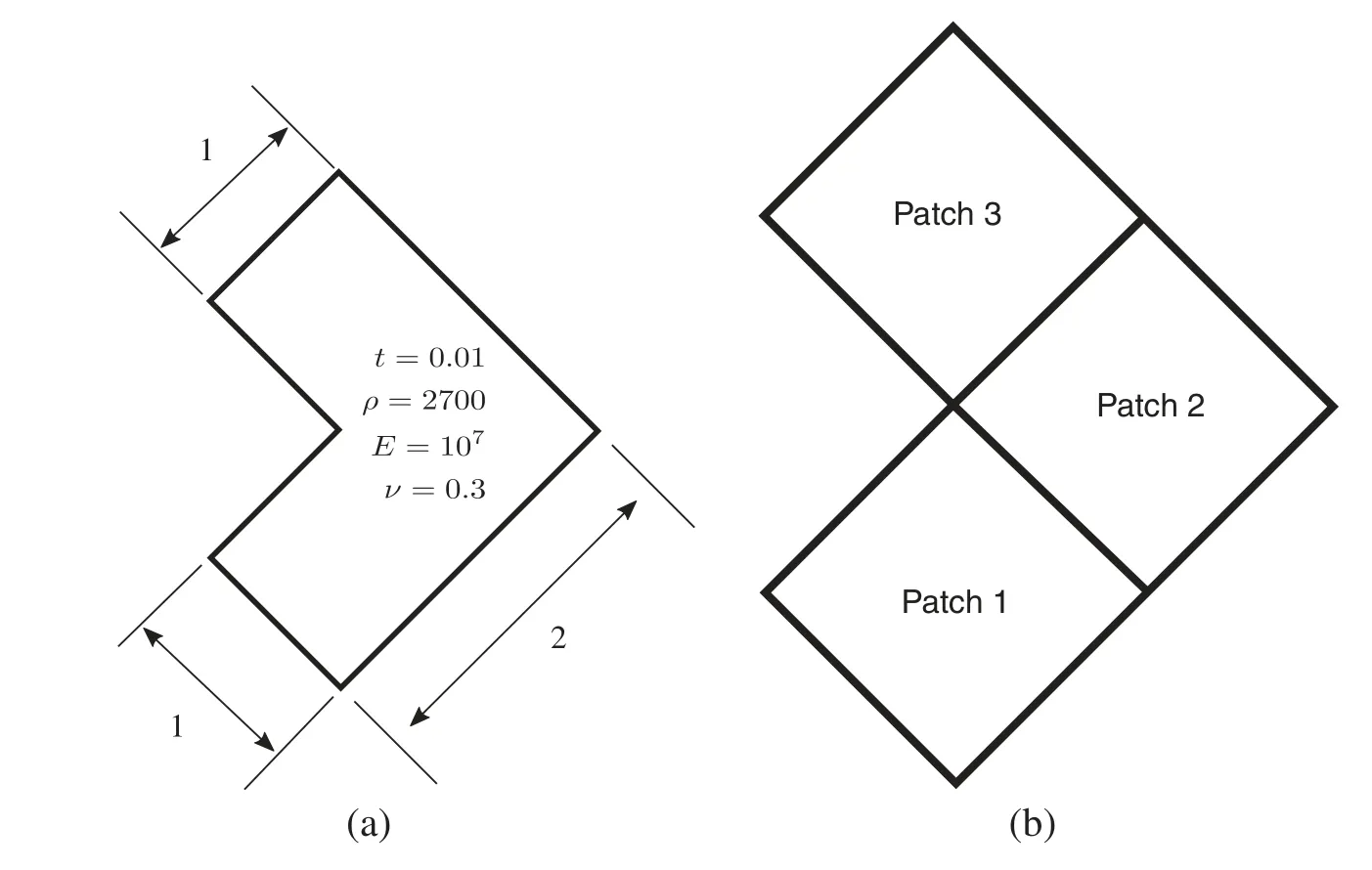
Figure 6:A simply supported heterogeneous L-shape plate:(a)geometric parameters and(b)discretization of patches,E2=E,E1=E3=1000E2

Figure 7:(Continued)

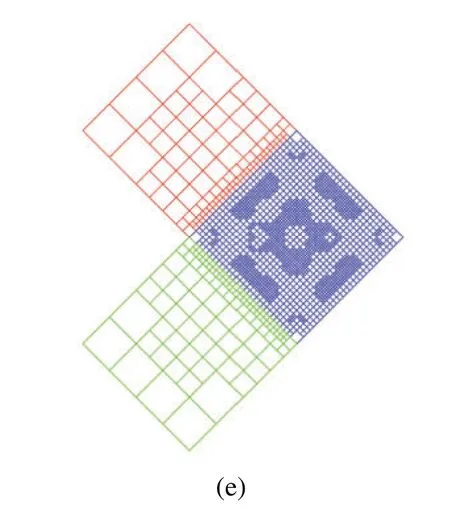
Figure 7:Adaptive refinement process of 1–15th mode for vibration of L-shape plate.Especially,2–3th,5–6th,7–8th,9–10th,12–13th,14–15th modes are multiple modes.Geometry-NURBS with order p1=1,p2=1;Solution Field-PHT with order q1=3,q2=3.(a)Initial mesh;(b)Adaptive mesh for 1th mode;(c)Adaptive mesh for 2–3,4th mode;(d)Adaptive mesh for 5–6,7–8th mode;(e)Adaptive mesh for 9–10,11,12–13,14–15th mode

6.3 Heterogeneous Plate with a Hole

In this section,a plate with a hole where the boundary simply supported is shown in Fig.11,consisting of two material Patches withE1=E=109,E2=100E1.Densityρis 2700,and thicknesshis 0.01 and Poisson’s rateνis 0.3.Consequently,the vibration response and local adaptive refinement is undoubtedly centralized in the Patch 2 area,seen in Figs.12 and 13.Different from L-shape example in Section 6.2,the geometry of the hole is non-linear so that cross-derivative of the parametrization in Eq.(16)are non-zero,which is a good opportunity to validate our algorithm is available in terms of non-linear mapping as well.The convergence rate plot of error indicators in both of Figs.14a and 15a support the reasonability of adopting refinement levelLe=1 for reference parametrization in solution field.Without any surprise,adaptive refinement performs a higher convergence rate than uniform refinement,based on an approximation of solution by a very fine mesh with 132,870 dof.

Figure 8:(Continued)

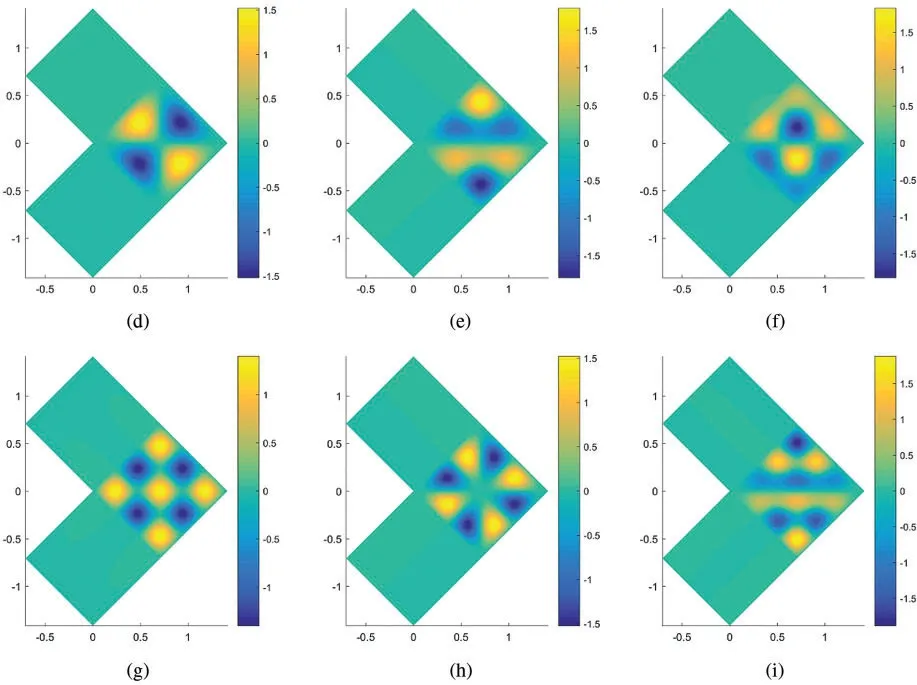
Figure 8:Mode shapes 1–15th of L-shape plate,where is normalized natural frequency at mode i,calculated by.(a) 1th mode,;(b) 2–3th mode,2.50;(c) 4th mode,;(d) 5–6th mode,;(e) 7–8th mode,6.50;(f) 9–10th mode,;(g) 11th mode,;(h) 12–13th mode,10.00;(i) 14–15th mode,

Figure 9:(Continued)

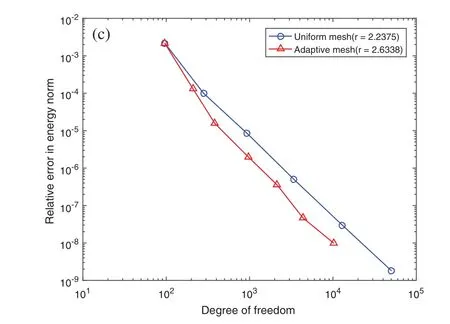
Figure 9:(a)Comparisons of error indicator of natural frequency at 1th mode among refinement level of Le=1,Le=2,Le=3;(b)error indicator of natural frequency of 1–15th mode during adaptive refinement process by sweeping modes;(c)contrast of relative error of natural frequency in energy norm at 1th mode between adaptive refinement and uniform refinement

Figure 10:(a)Comparisons of error indicator of eigenvector at 1th mode among refinement level of Le=1,Le=2,Le=3;(b)error indicator of eigenvector of 1–15th mode during adaptive refinement process by sweeping modes;(c)contrast of relative error of eigenvector in energy norm between adaptive refinement and uniform refinement

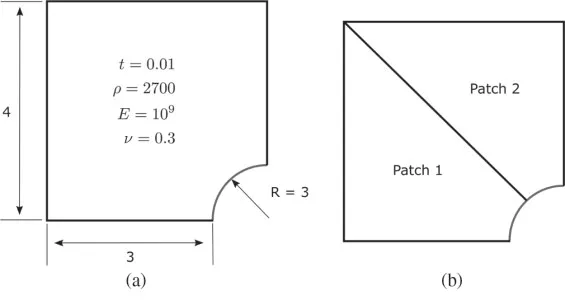
Figure 11:A simply supported heterogeneous platehole:(a)geometric parameters and(b)discretization of patches,E1=E,E2=100E1

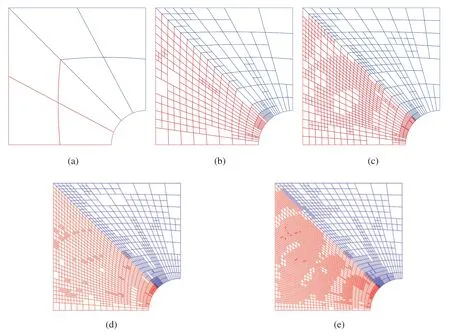
Figure 12:Adaptive refinement process of 1–9th mode for vibration of platehole.Geometry-NURBS with order p1=1,p2=2;Solution Field-PHT with order q1=3,q2=3

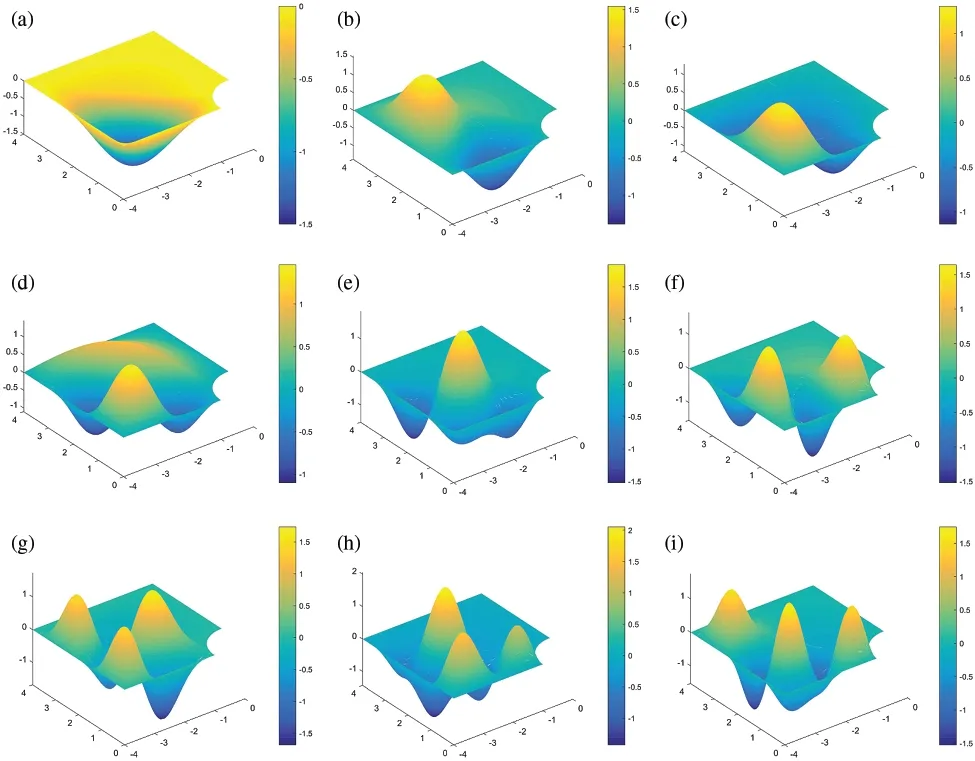
Figure 13:Mode shapes 1–9th of platehole,where is normalized natural frequency at mode i,calculated by(a) 1th mode,;(b) 2th mode,2.03;(c) 3th mode,;(d) 4th mode,;(e) 5th mode,3.52;(f) 6th mode,;(g) 7th mode,;(h) 8th mode,;(i) 9th mode,

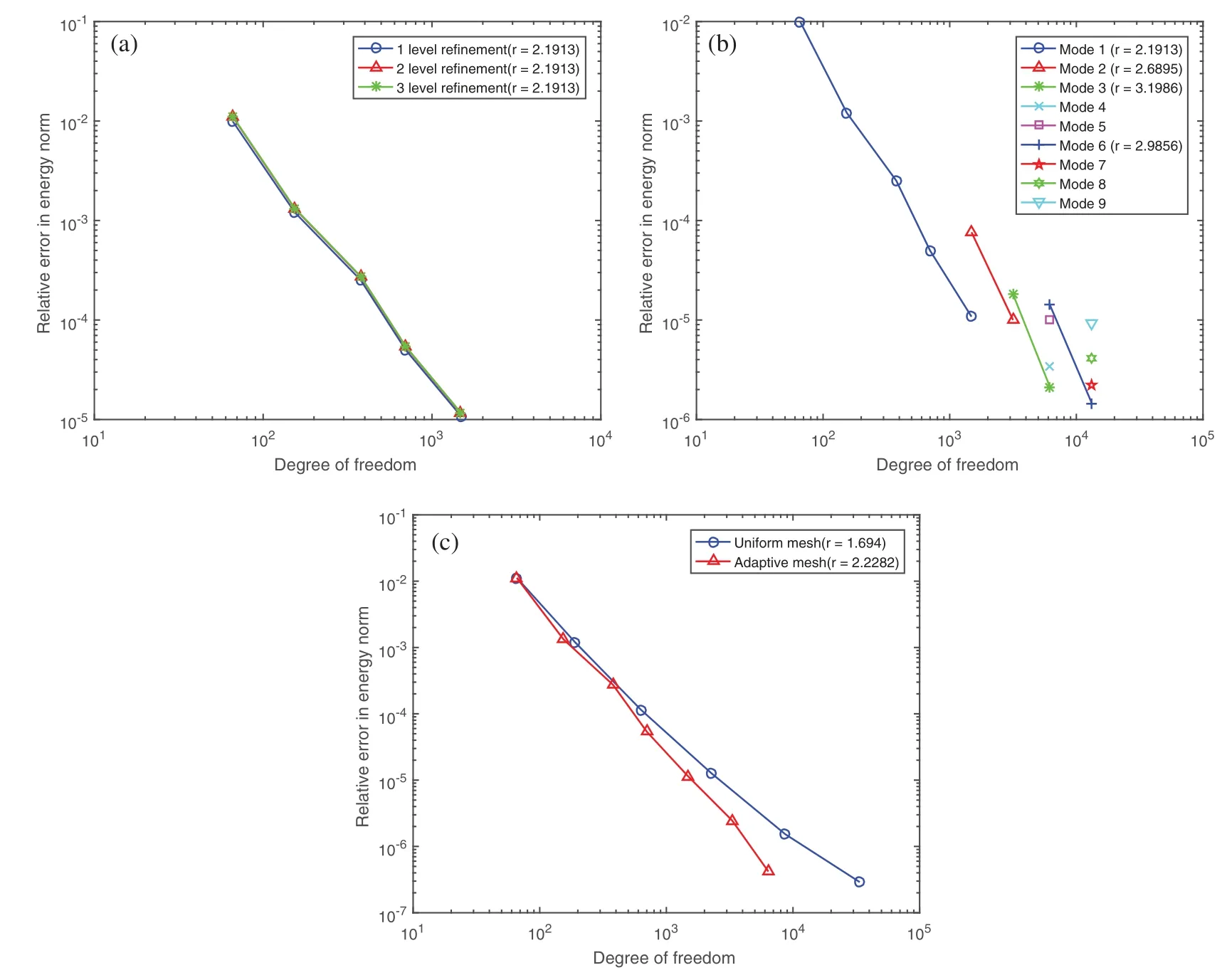
Figure 14:(a)Comparisons of among refinement level of Le=1,Le=2,Le=3;(b)error indicator of natural frequency of 1–9th mode during adaptive refinement process by sweeping modes;(c)contrast of relative error of natural frequency in energy norm at 1th mode between adaptive refinement and uniform refinement

Figure 15:(Continued)

Figure 15:(a)Comparisons of among refinement level of Le=1,Le=2,Le=3;(b)error indicator of eigenvector of 1–9th mode during adaptive refinement process by sweeping modes;(c)contrast of relative error of eigenvector in energy norm between adaptive refinement and uniform refinement

6.4 Heterogeneous Lshaped-Bracket

The L-shape bracket is such a complex structure that it is divided into 18 Patches in Fig.16b.Patches 1–4 are softer than other Patches thatE1-4=E,E5-18=100E=109.Densityρis 2700,and thicknesshis 0.01 and Poisson’s rateνis 0.3.The whole boundary including the 4 holes is imposed to be simply supported except the right edge marked with red colour in Fig.16a,where the boundary condition is assumed to be free.It is intended to make the vibration around Patch 4 is more fiercely than other parts.As a consequence,at the first 5 modes(1th–5th),the structural vibration and adaptive local refinement merge into Patches 1–4.When it comes to the 6th mode,the mode shape moves to the middle of structure(Patch 9,10),seen in Fig.18f.It induces the rise of the error(proved by plot of Mode 6 in Figs.19b and 20b,respectively in this district and certainly the adaptive refinement will locate nearby,seen in Fig.17e.After that,the modal shape moves back to Patches 1–4 and the adaptivity keeps going on in that zone.The convergence rate between adaptive refinement and uniform refinement are computed upon the basis of an approximate solution with 301,470 dof.Apparently,in Figs.19c and 20,the convergence rate of adaptive refinement is much steeper(more than twice)than that of uniform refinement.This indicates the structural response is much local in this problem.

Figure 16:A simply supported with right free boundary heterogeneous Lshaped-bracket:(a)geometric parameters and(b)discretization of patches,E1-4=E,E5-18=100E

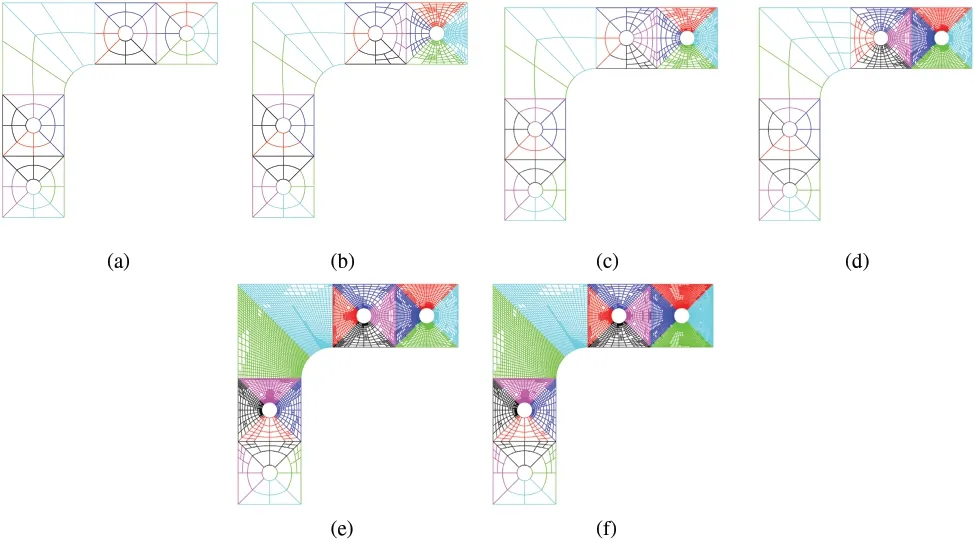
Figure 17:Adaptive refinement process of 1–9th mode for vibration of Lshaped-bracket.Geometry-NURBS with order p1=1,p2=2;Solution Field-PHT with order q1=3,q2=3.(a)Initial mesh;(b)Adaptive mesh for 1th mode;(c)Adaptive mesh for 2th mode;(d)Adaptive mesh for 3,4,5th mode;(e)Adaptive mesh for 6,7th mode;(f)Adaptive mesh for 8,9th mode

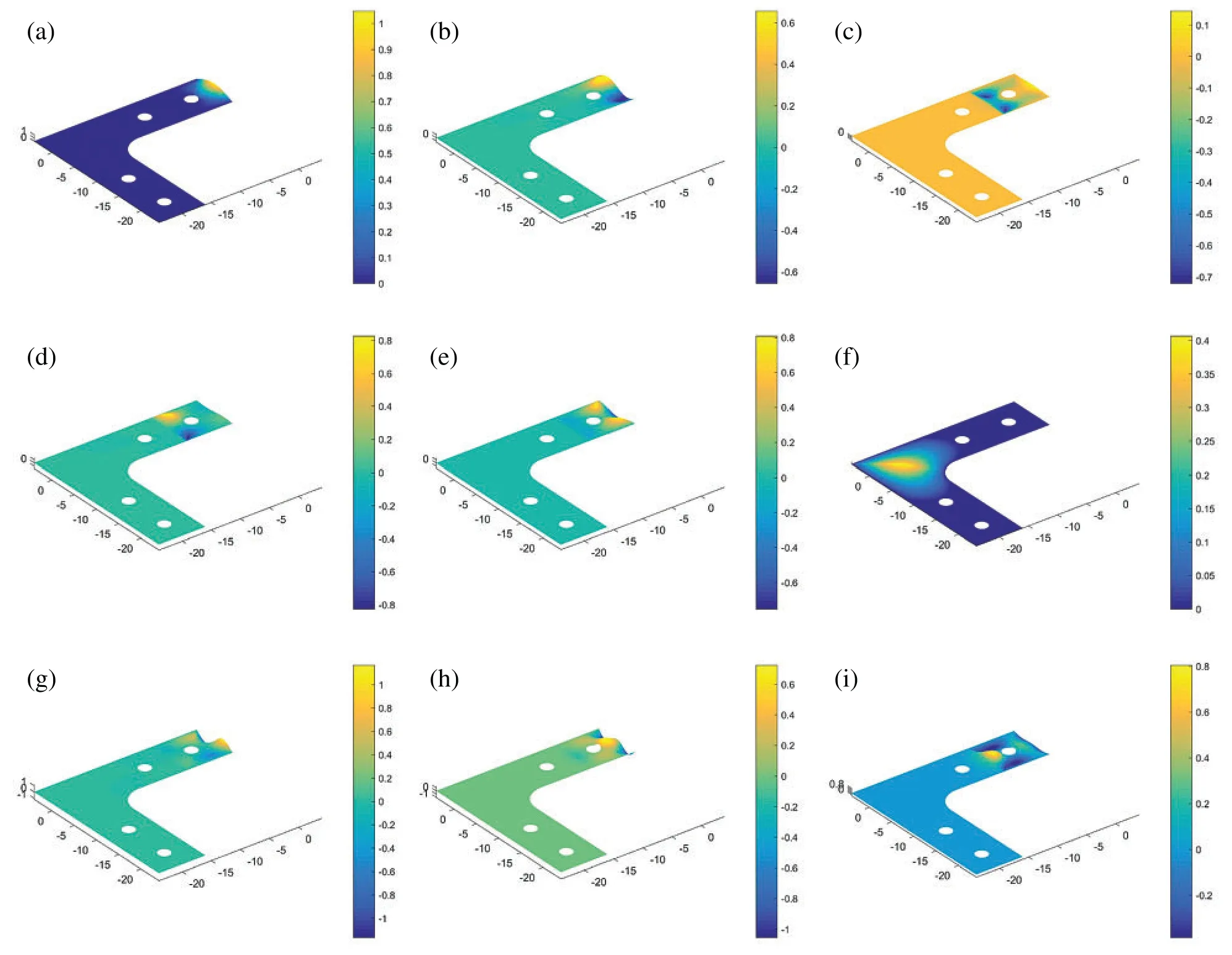
Figure 18:Mode shapes 1–9th of Lshaped-bracket,where is normalized natural frequency at mode i,calculated by λiN=λi/λ1,i=1,2,3...n.(a) 1th mode,;(b) 2th mode,2.79;(c) 3th mode,;(d) 4th mode,;(e) 5th mode,3.77;(f) 6th mode,;(g) 7th mode,;(h) 8th mode,;(i) 9th mode,

Figure 19:(a)Comparisons of among refinement level of Le=1,Le=2,Le=3;(b)error indicator of natural frequency of 1–15th mode during adaptive refinement process by sweeping modes;(c)contrast of relative error of natural frequency in energy norm between adaptive refinement and uniform refinement

Figure 20:(a)Comparisons of error indicator of eigenvector at 1th mode among refinement level of Le=1,Le=2,Le=3;(b)error indicator of eigenvector of 1–15th mode during adaptive refinement process by sweeping modes;(c)contrast of relative error of eigenvector in energy norm between adaptive refinement and uniform refinement

7 Conclusion

In this article,based on our proposed adaptivity strategy in the framework of GIFT paradigm utilized for vibration of Reissner–Mindlin plate,it is developed to investigate the error-driven adaptivity for structural vibration of Kirchhoff plate.GIFT offers us the convenience to choose solution field independently from geometry so that the good accuracy can be achieved by better approximation in the solution field even though the geometric parameterization is not fairly designed as supported by the example in Section 6.1.Furthermore,it allows us to connect NURBS describing for geometry with PHT represented for solution field to reserve geometric precision and realize local refinement.Besides,when dealing with error estimation process,MAC scheme is helpful to locate the correspondence of modal vectors covering multiple eigenvectors between two different meshes.Our error indicator is proved to be reasonably chosen and the proposed adaptive strategy shows a better convergence rate than uniform refinement,supported by numerical tests in Sections 6.2–6.4.

We believe the proposed algorithm has potential to be practical in engineering problems.The developed method is available to precisely describe complex geometry of structure and simultaneously saves computational resource for given accuracy,especially for structures with local mechanical behaviour.As to the adaptivity of vibration by sweeping modes from low to high frequency,this adaptive strategy can be started from any mode or used to optimize some specific modes people are interested in.It would be productive to modal analysis for vibration problem.In the future,we intend to extend this method to 3D elasto-dynamics including the space-time problems.

Acknowledgement:This study was funded by Research Grant for 100 Talents of Guangxi Plan,The Starting Research Grant for High-Level Talents from Guangxi University,Generalized Isogeometric Analysis with Homogeniztion Theory for Soft Acoustic Metamaterials(20200312),Science and Technology Major Project of Guangxi Province(AA18118055),Guangxi Natural Science Foundation(2018JJB160052),and Application of Key technology in Building Construction of Prefabricated Steel Structure(BB30300105).

Funding Statement:This study was funded by Natural Science Foundation of China(Grant No.12102095),Research grant for 100 Talents of Guangxi Plan,The Starting Research Grant for High-Level Talents from Guangxi University,Generalized Isogeometric Analysis with Homogeniztion Theory for Soft Acoustic Metamaterials(AD20159080),Science and Technology Major Project of Guangxi Province(AA18118055),Guangxi Natural Science Foundation(2018JJB160052),and Application of Key Technology in Building Construction of Prefabricated Steel Structure(BB30300105).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.