An Improved Gorilla Troops Optimizer Based on Lens Opposition-Based Learning and Adaptive β-Hill Climbing for Global Optimization

Yaning Xiao,Xue Sun,Yanling Guo,Sanping Li,Yapeng Zhang and Yangwei Wang

College of Mechanical and Electrical Engineering,Northeast Forestry University,Harbin,150040,China

ABSTRACT Gorilla troops optimizer(GTO)is a newly developed meta-heuristic algorithm,which is inspired by the collective lifestyle and social intelligence of gorillas.Similar to other metaheuristics,the convergence accuracy and stability of GTO will deteriorate when the optimization problems to be solved become more complex and flexible.To overcome these defects and achieve better performance,this paper proposes an improved gorilla troops optimizer(IGTO).First,Circle chaotic mapping is introduced to initialize the positions of gorillas,which facilitates the population diversity and establishes a good foundation for global search.Then,in order to avoid getting trapped in the local optimum,the lens opposition-based learning mechanism is adopted to expand the search ranges.Besides,a novel local search-based algorithm,namely adaptive β-hill climbing,is amalgamated with GTO to increase the final solution precision.Attributed to three improvements,the exploration and exploitation capabilities of the basic GTO are greatly enhanced.The performance of the proposed algorithm is comprehensively evaluated and analyzed on 19 classical benchmark functions.The numerical and statistical results demonstrate that IGTO can provide better solution quality,local optimum avoidance,and robustness compared with the basic GTO and five other wellknown algorithms.Moreover,the applicability of IGTO is further proved through resolving four engineering design problems and training multilayer perceptron.The experimental results suggest that IGTO exhibits remarkable competitive performance and promising prospects in real-world tasks.

KEYWORDS Gorilla troops optimizer;circle chaotic mapping;lens opposition-based learning;adaptive β-hill climbing

1 Introduction

Optimization refers to the process of searching for the optimal solution to a particular issue under certain constraints,so as to maximize benefits,performance and productivity[1–4].With the help of optimization techniques,a large number of problems encountered in different applied disciplines could be solved in a more efficient,accurate,and real-time way[5,6].However,with the increasing complexity of global optimization problems nowadays,conventional mathematical methods based on gradient information are challenged by high-dimensional,suboptimal regions,and large-scale search ranges that cannot adapt to the real requirements[7,8].The development of more effective tools to settle these complex NP-hard problems is an indivisible research hotspot.Compared to traditional approaches,meta-heuristic algorithms(MAs)are often able to obtain the global best results on such problems,which is attributed to the merits of their simple structure,ease of implementation,as well as strong capability to bypass the local optimum[9,10].As a result,during the past few decades,MAs have entered the blowout stage and received major attention from worldwide scholars[11–13].

MAs find out the optimal solution through the simulation of stochastic phenomena in nature.Based on the different design concepts,the nature-inspired MAs may be generally classified into four categories[14–16]:evolution-based,physical-based,swarm-based,and human-based algorithms.Specifically,evolutionary algorithms emulate the laws of Darwinian natural selection theory,and some well-regarded cases of which are Genetic Algorithm(GA)[17],Differential Evolution(DE)[18],and Biogeography-Based Optimization(BBO)[19].Physical-based algorithms simulate the physical phenomenon of the universe such as Simulated Annealing(SA)[20],Multi-Verse Optimizer(MVO)[21],Thermal Exchange Optimization(TEO)[22],Atom Search Optimization(ASO)[23],and Equilibrium Optimizer(EO)[24],etc.Swarm-based algorithms primarily originate from the collective behaviours of social creatures.A remarkable embodiment of this category of algorithms is Particle Swarm Optimization(PSO)[25],which was first proposed in 1995 based on the foraging behaviour of birds.Ant Colony Optimization(ACO)[26],Chicken Swarm Optimization(CSO)[27],Dragonfly Algorithm(DA)[28],Whale Optimization Algorithm(WOA)[29],Spotted Hyena Optimizer(SHO)[30],Emperor Penguin Optimizer(EPO)[31],Seagull Optimization Algorithm(SOA)[32],Harris Hawks Optimization(HHO)[33],Tunicate Swarm Algorithm(TSA)[34],Sooty Tern Optimization Algorithm(STOA)[35],Slime Mould Algorithm(SMA)[36],Rat Swarm Optimizer(RSO)[37],and Aquila Optimizer(AO)[38]are also essential parts in this branch.The final type is influenced by human learning habits including Search Group Algorithm(SGA)[39],Soccer League Competition Algorithm(SLC)[40],and Teaching-Learning-Based Optimization(TLBO)[41].

With their own distinctive characteristics,these metaheuristics are commonly used in a variety of computing science fields,such as fault diagnosis[42],feature selection[43],engineering optimization[44],path planning[45],and parameters identification[46].Nevertheless,it has been shown that the most basic algorithms still have the limitations of slow convergence,poor accuracy,and ease of getting trapped into the local optimum[7,15]in several applications.The non-free lunch(NFL)theorem indicates that there is no general algorithm that could be appropriate for all optimization tasks[47].Hence,encouraged by this theorem,many scholars begin improving existing algorithms to generate higher-quality solutions from different aspects.Fan et al.[7]proposed an enhanced Equilibrium Optimizer(m-EO)algorithm based on reverse learning and novel updating mechanisms,which considerably increase its convergence speed and precision.Jia et al.[48]introduced the dynamic control parameter and mutation strategies into the Harris Hawks Optimization,and then proposed a novel method called DHHO/M to segment satellite images.Ding et al.[49]constructed an improved Whale Optimization Algorithm(LNAWOA)for continuous optimization,in which the nonlinear convergence factor is utilized to speed up the convergence.Besides,authors in[50]employed Lévy flight and crossover operation to further promote the robust and global exploration capability of the native Salp Swarm Algorithm.Recently,there is also an emerging trend to combine two prospective MAs to overcome the performance drawbacks of one single algorithm.For instance,Abdel-Basset et al.[51]incorporated Slime Mould Optimizer and Whale Optimization Algorithm into an efficient hybrid algorithm(HSMAWOA)for image segmentation of chest X-ray to determine whether a person is infected with the COVID-19 virus.Fan et al.[9]proposed a new hybrid algorithm named ESSAWOA,which has been successfully applied to solve structural design problems.Moreover,Liu et al.[52]developed a hybrid imperialist competitive evolutionary algorithm and used it to find out the best portfolio solutions.Dhiman[53]constructed a hybrid bio-inspired Emperor Penguin and Salp Swarm Algorithm(ESA)for numerical optimization that effectively deals with different constraint problems in engineering optimization.

In this study,we focus on a novel swarm intelligent algorithm namely Gorilla Troops Optimizer(GTO),which was proposed by Abdollahzadeh et al.in 2021[54].The inspiration of GTO originates from the collective lifestyle and social intelligence of gorillas.Preliminary research indicates that GTO has excellent performances on benchmark function optimization.Nevertheless,similar to other meta-heuristic algorithms,it still suffers from low optimization accuracy,premature convergence,and the propensity to fall into the local optimum when solving complex optimization problems[55].These defects are mainly associated with the poor quality of the initial population,lack of a proper balance between the exploration and exploitation,and low likelihood of large spatial leaps in the iteration process.Therefore,NFL theorem motivates us to improve this latest swarm-inspired algorithm.

In view of the above discussion,to enhance GTO for global optimization,an improved gorilla troops optimizer known as IGTO is developed in this paper by incorporating three improvements.Firstly,Circle chaotic mapping is utilized to replace the random initialization mode of GTO for enriching population diversity.Secondly,a novel lens opposition-based learning mechanism is adopted to boost the exploration capability of the algorithm,while avoiding falling into the local optimum.Additionally,adaptive β-hill climbing,a new local search algorithm is embedded into GTO to facilitate better solution accuracy and exploitation trends.The effectiveness of the proposed IGTO is comprehensively evaluated and investigated by a series of comparisons with the basic GTO and several state-of-the-art algorithms,including GWO,WOA,SSA,HHO,and SMA on 19 classical benchmark functions.The experimental results demonstrate that IGTO performs better than the other competitors in terms of solution quality,convergence accuracy and stability.In addition,to further validate its applicability,IGTO is applied to solve four engineering design problems and train multilayer perceptron.Our results reveal that the proposed method also has strong competitiveness and superiority in real-life applications.

The remainder of this paper is arranged as follows:the basic GTO algorithm is briefly described in Section 2.In Section 3,a detailed description of three improved mechanisms and the proposed IGTO is presented.In Section 4,the experimental results of benchmark function optimization are reported and discussed.Besides,the applicability of the IGTO for resolving practical engineering problems and training multilayer perceptron is highlighted and analyzed in Sections 5 and 6.Finally,the conclusion of this work and potential future work directions are given in Section 7.

2 Gorilla Troops Optimizer

Gorilla troops optimizer is a recently proposed nature-inspired and gradient-free optimization algorithm,which emulates the gorillas’lifestyle in the group[54].The gorilla lives in a group called troop,composed of an adult male gorilla also known as the silverback,multiple adult female gorillas and their posterity.A silverback gorilla(shown in Fig.1)typically has an age of more than 12 years and is named for the unique hair on his back at puberty.Besides,the silverback is the head of the whole troop,taking all decisions,mediating disputes,directing others to food resources,determining group movements,and being responsible for safety.Younger male gorillas at the age of 8 to 12 years are called blackbacks since they still lack silver-coloured back hairs.They are affiliated with the silverback and act as backup defenders for the group.In general,both female and male gorillas tend to migrate from the group where they were born to a second new group.Alternatively,mature male gorillas are also likely to separate from their original group and constitute troops for their own by attracting migrating females.However,some male gorillas sometimes choose to stay in the initial troop and continue to follow the silverback.If the silverback dies,these males might engage in a brutal battle for dominance of the group and mating with adult females.Based on the above concept of gorillas group behaviour in nature,the specific mathematical model for the GTO algorithm is developed.As with other intelligent algorithms,GTO contains three main parts:initialization,global exploration,and local exploitation,which are explained thoroughly below.

Figure 1:Silverback gorilla[54]

2.1 Initialization Phase

Suppose there areNgorillas in theD-dimensional space.The position of thei-th gorilla in the space can be defined asXi=(xi,1,xi,2,···,xi,D),i=1,2,···,N.Thus,the initialization process of gorilla populations can be described as:

whereubandlbare the upper and lower boundaries of the search range,respectively,andrand(N,D)denotes the matrix withNrows andDcolumns,where each element is a random number between 0 and 1.

2.2 Exploration Phase

Once gorillas depart from their original troop,they will move to diverse environments in nature that they might or might not have ever seen before.In the GTO algorithm,all gorillas are considered as candidate solutions,and the optimal solution in each optimization process is deemed to be the silverback.In order to accurately simulate such natural behaviour of migration,the position update equation of the gorilla for the exploration stage was designed by employing three different approaches including migrating towards unknown positions,migrating around familiar locations,and moving to other groups,as shown in Eq.(2):

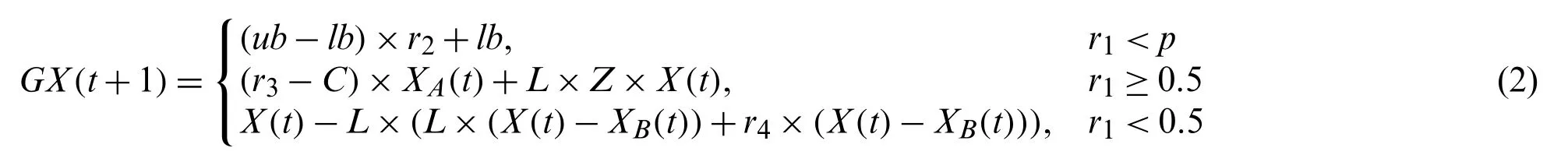
wheretindicates the current iteration times,X(t)denotes the current position vector of the individual gorilla,andGX(t+1)refers to the candidate position of search agents in the next iteration.Besides,r1,r2,r3andr4are all the random values between 0 and 1.XA(t)andXB(t)are two randomly selected gorilla positions in the current population.pis a constant.Zdenotes a row vector in the problem dimension with values of the element are randomly generated in[-C,C].And the parameterCis calculated according to Eq.(3).

wherecos(·)represents the cosine function,r5is a random number in the range of 0 to 1,andMaxiterindicates the maximum iterations.

As for the parameterLin Eq.(2)could be computed as follows:

wherelis a random number in between[-1,1].

Upon the completion of the exploration,the fitness values of all newly generated candidateGX(t+1)solutions are evaluated.Provided thatGXis better thanXi.e.,F(GX)＜F(X),whereF(·)denotes the fitness function for a certain problem,it will be retained and replace the original solutionX(t).In addition,the optimal solution at this period is selected as the silverbackXsilverback.

2.3 Exploitation Phase

When the troop was just established,the silverback is powerful and healthy,while the others male gorillas are still young.They obey all the decisions of silverback in search of diverse food resources and serve the silverback gorilla faithfully.Undeniably speaking,the silverback also grows old and then finally dies,with younger blackbacks in the troop might get involved into a violent conflict with the other males for mating with the adult females and the leadership.As mentioned previously,two behaviours of following the silverback and competing for adult female gorillas are modelled in the exploitation phase of GTO.At the same time,the parameterWis introduced to control the switch between them.If the valueCin Eq.(3)is greater thanW,the first mechanism of following the silverback is elected.The mathematical expression is as follows:

whereLis also evaluated using Eq.(4),Xsilverbackrepresents the best solution obtained so far,andX(t)denotes the current position vector.In addition,the parameterMcould be calculated according to Eq.(6):

whereNrefers to the population size,andXi(t)denotes each position vector of the gorilla in the current iteration.

IfC ＜W,it implies that the latter mechanism is chosen,in this case,the location of gorillas can be updated as follows:

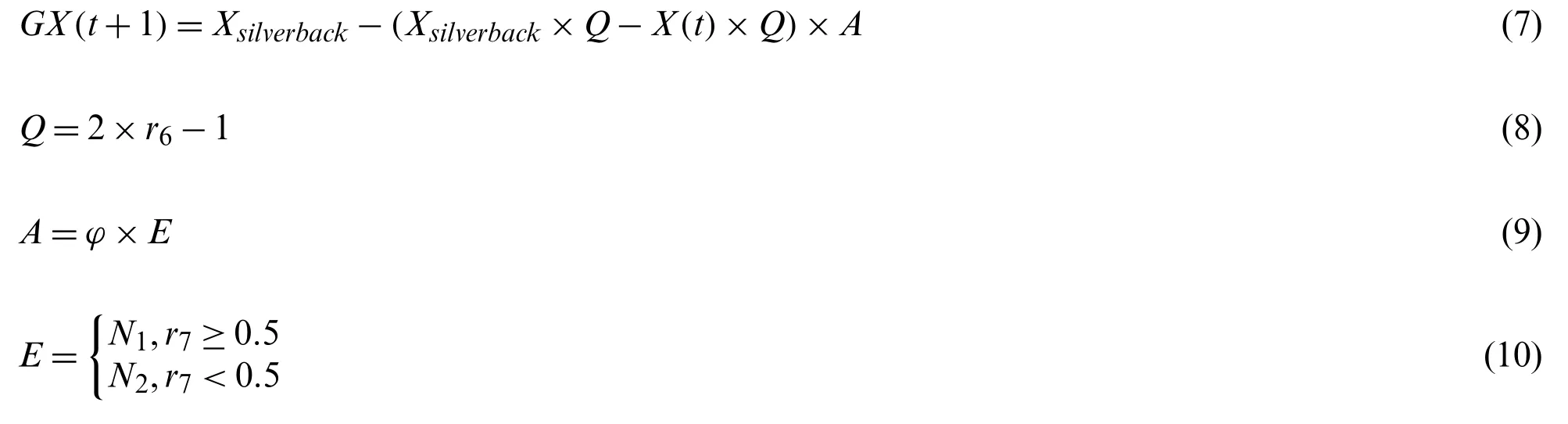
In Eq.(7),X(t)denotes the current position andQstands for the impact force,which is computed using Eq.(8).In Eq.(8),r6is a random value in the range of 0 to 1.Moreover,the coefficientAused to mimic the violence intensity in the competition is evaluated by Eq.(9),whereφdenotes a constant and the values ofEare assigned with Eq.(10).In Eq.(10),r7is also a random number in[0,1].Ifr7≥0.5,Ewould be defined as a 1-by-Darray of normal distribution random numbers,andDis the spatial dimension.Instead,ifr7＜0.5,Ewould be equal to a stochastic number that obeys the normal distribution.

Similarly,at the end of the exploitation process,the fitness values of the newly generated candidateGX(t+1)solution are also calculated.IfF(GX)＜F(X),the solutionGXwill be preserved and participate in the subsequent optimization,while the optimal solution within all individuals is defined as the silverbackXsilverback.The pseudo-code of GTO is shown in Algorithm 1.

Algorithm 1:Gorilla troops optimizer 1:Initialize the population size N and the maximum number of iterations Maxiter 2:Initialize the random gorilla population Xi(i=1,2,···,N)3:Calculate the fitness values of all gorilla individuals 4:While t ＜Maxiter do 5:Update the parameter C according to Eq.(3)6:Update the parameter L according to Eq.(4)7:For each gorilla Xi do // Exploration stage 8:Update the position of the current gorilla according to Eq.(2)9:End For 10:Evaluate the fitness values of all gorillas 11:Save the optimal solution as a silverback Xsilverback 12:For each gorilla Xi do // Exploitation stage 13:If C ≥W then 14:Update the position of current gorilla according to Eq.(5)15:Else 16:Update the position of current gorilla according to Eq.(7)17:End If 18:End For

Algorithm 1(Continued)19:Update the fitness values of all gorillas 20:Update the global best solution Xsilverback 21:t=t+1 22:End While 23:Output the global best solution Xsilverback and its fitness value

3 The Proposed IGTO Algorithm

In order to further improve the performance of the basic GTO algorithm for global optimization,a novel variant named IGTO is presented in this section.First,Circle chaotic mapping is adopted to initialize the gorilla populations,which is considered from increasing the population diversity.Second,an effective lens opposition-based learning strategy is implemented to expand the search range and avoid the algorithm falling into the local optimum.Final,the modified algorithm is hybridized with the adaptive β-hill climbing for better exploitation trend and solution quality.The specific process is figured out as follows.

3.1 Circle Chaotic Mapping

It is indicated that the quality of the initial population individuals has a significant impact on the efficiency of most current metaheuristic algorithms[49,56].When applying the GTO algorithm to tackle an optimization problem,the population is usually initialized by means of a stochastic search.Though this method is accessible to implement,yet it suffers from a lack of ergodicity and excessively depends on the probability distribution,which cannot guarantee that the initial population is uniformly distributed in the search space,thereby deteriorating the solution precision and convergence speed of the algorithm.

Chaotic mapping is a complex dynamic method found in nonlinear systems with the properties of unpredictability,randomness,and ergodicity.Compared to random distribution,chaotic mapping allows the initial population individual to explore the solution space thoroughly with a higher convergence speed and sensitivity so that it is widely adopted to improve the optimization performance of algorithms.Research results have proven that Circle chaotic mapping has superior exploration performance than the commonly used Logistic chaotic mapping and Tent chaotic mapping[57].Consequently,in order to boost the population diversity and take full advantage of the information in the solution space,Circle chaotic mapping is introduced in this study to improve the initialization mode of the basic GTO.And the mathematical expression of Circle chaotic mapping is as follows:

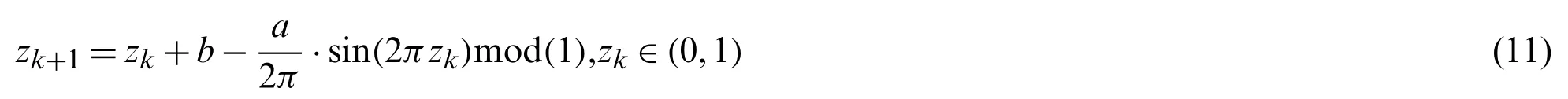
wherea=0.5 andb=0.2.Under the same free independent parameters,the random search mechanism and Circle mapping are selected to be executed independently 300 times.Besides,the obtained results are shown in Fig.2.It can be seen from the figure that the traversal of Circle chaotic mapping is wider and more homogeneously distributed in the feasible domain[0,1]than that of random search.Hence,the proposed algorithm has a more robust global exploration ability after incorporating Circle chaotic mapping.

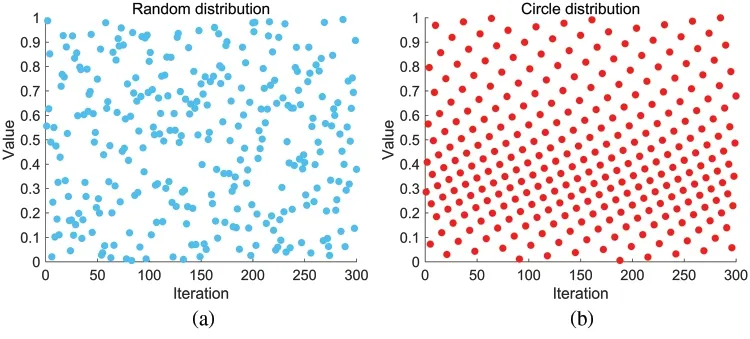
Figure 2:Distributions of random search and circle chaotic mapping.(a)Random distribution(b)Circle distribution

The pseudo-code for initializing the population using Circle chaotic mapping is outlined in Algorithm 2.

Algorithm 2:Circle chaotic mapping 1:Initialize the population size N and the dimension D 2:Randomly generate the initial value z0 in the range[0,1]3:For i=1 to N do 4:For k=1 to D do 5:Generate the chaotic variable zk according to Eq.(11)6:Si,k=zk 7:End For 8:Map the sequence Si into the search interval of gorillas: Xi=Si×(ub-lb)+lb 9:End For 10:Return Xi(i=1,2,···,N) as the initialized population matrix

3.2 Lens Opposition-Based Learning

As a novel technique in the area of smart computing,lens opposition-based learning(LOBL),incorporating traditional opposition-based learning(OBL)[58]and convex lens imaging discipline,has been successfully employed in different intelligent algorithm optimizations[59,60].Its basic ideology is to simultaneously calculate and compare the candidate solution and corresponding reverse solution,and then choose the superior one to proceed with the next iteration.Theoretically demonstrated by Fan et al.[9],LOBL can produce a solution close to the global optimum with higher possibility.Therefore,in this study,LOBL is utilized to update the candidate solutions during the exploration phase,in order to enlarge the search range and help the algorithm to escape from the local optimum.Several conceptions about LOBL are represented mathematically as follows.

Lens imaging is a physical optics phenomenon,which refers to the fact that while an object is located at more than two principal focal lengths away from the convex lens,a smaller and inverted image will be produced on the opposite side of the lens.Taking the one-dimensional search space in Fig.3 for illustration,there is a convex lens with the focal lengthfset at the base pointO(the midpoint of search range[lb,ub]).Besides,an objectpwith the heighthis placed on the coordinate axis,and its projection isGX(the candidate solution).Distance from the object to the lensuis greater than twicef.Through the lens imaging operation,an inverted imagingp′of heighth*could be attained,which is projected asGX*(the reverse solution)on thex-axis.In accordance with the rules of lens imaging as well as similar triangle,the geometrical relationship obtained from Fig.3 can be expressed as:

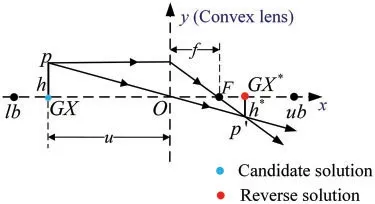
Figure 3:The principle of LOBL mechanism

Here,let the scale factorn=h/h*,the reverse solutionGX*is calculated by transferring the Eq.(12):

It is obvious that whenn=1,Eq.(13)can be simplified as the general formulation of OBL strategy:

So,we could regard the opposition-based learning strategy as a peculiar case of LOBL.In comparison to OBL,the latter allows acquiring dynamic reverse solutions and a wider search range by tuning the scale factorn.

Generally,Eq.(13)could be extended intoD-dimensional space:

wherelbjandubjare the lower and upper limits of thej-th dimension,respectively,j=1,2,···D,denotes the inverse solution ofGXjin thej-th dimension.

When a new inverse solution is generated,there is no guarantee that it is always better than the current candidate solution as in the gorilla position.Therefore,it is necessary to evaluate the fitness values of the inverse solution and candidate solution,then the fitter one will be selected to continue participating in the subsequent exploitation phase,which is described as follows:

whereGX*indicates the reverse solution generated by LOBL,GXis the current candidate solution,GXnextis the selected gorilla to continue the subsequent position updating,andF(·)denotes the fitness function of the problem.The pseudo-code of lens opposition-based learning mechanism is shown in Algorithm 3.

Algorithm 3:Lens opposition-based learning 1:Input the current candidate solution of gorilla GX,the dimension D and scale factor n 2:For j=1 to D do 3:Generate the reverse solution GX* using Eq.(15)4:End For 5:Calculate the fitness values of GX and GX*6:If F(GX*)＜F(GX) then 7:GXnext=GX*8:End If 9:Output the new candidate solution GXnext

3.3 Adaptive β-Hill Climbing

Adaptive β-hill climbing(AβHC)[61]is a newly proposed local search-based algorithm,which is,in essence,a modified version of β-hill climbing(βHC).Research has found that AβHC provides better performance than many other famous local search algorithms,including Simulated Annealing(SA)[20],Tabu Search(TS)[62],and Variable Neighborhood Search(VNS)[63].To boost the algorithm’s exploitation ability and the quality of final solutions,AβHC is integrated into the basic GTO to help search the neighborhoods of the optimal solution in this study.And the definition of AβHC is represented mathematically as follows.

For the given current solutionXi=(xi,1,xi,2,...,xi,D),AβHC will iteratively generate an enhanced solutionon the basis of two control operators:Noperator andβ-operator.The N-operator first transfersXito a new neighborhood solutionwhich is defined in Eqs.(17)and(18)as:

whereU(0,1)denotes a random number in the interval[0,1],xi,jdenotes the value of the decision variable in thej-th dimension,tdenotes the current iteration,Maxiterrefers to the maximum number of iterations,N represents the bandwidth distance between the current solution and its neighbor,Dis the spatial dimension,and the parameterKis a constant.

Immediately after,the decision variables of new solutionare assigned either from the existing solution or randomly from the available range ofβ-operator,as follows:

wherer8is a random number in the interval[0,1],xi,rdenotes another random number chosen from the possible range of that particular dimension of the problem,βmaxandβmindenote the maximum and minimum values of probability valueβ∈[0,1],respectively.If the generated solutionis better than the current solution under considerationXi,thenXiis replaced by.The pseudo-code of adaptive β-hill climbing is given in Algorithm 4.

Algorithm 4:Adaptive β-hill climbing algorithm 1:Initialize the parameters βmax,βmin,and K 2:Input the current solution Xi=(xi,1,xi,2,...,xi,D)3:Calculate the fitness value F(Xi)4:While t ≤Maxiter do 5:Generate the neighbouring solution X′i using Eq.(17)6:For j=1 to D do 7:If r8 ＜then 8:x′′i,j=xi,r 9:Else 10:x′′i,j=x′i,j 11:End If 12:End For 13:Calculate the fitness value F(X′′i )14:If F(X′′i )＜F(Xi) then 15:Xi=X′′i 16:End If 17: t=t+1 18:End while

3.4 Algorithm Flowchart

Based on the improved mechanisms mentioned in Subsections 3.1～3.3 above,the flowchart of the proposed IGTO algorithm for global optimization problems is illustrated in Fig.4.Moreover,Algorithm 5 outlines the pseudo-code of IGTO.

Algorithm 5:Improved gorilla troops optimizer 1:Initialize the population size N and the maximum number of iterations Maxiter 2:Initialize the chaotic gorilla population Xi using Circle chaotic mapping 3:Calculate the fitness values of all gorilla individuals 4:While t ＜Maxiter do 5:Update the parameter C according to Eq.(3)6:Update the parameter L according to Eq.(4)7:For each gorilla do //Exploration stage 8:Update the position of the current gorilla according to Eq.(2)9:Calculate and evaluate the candidate position and its reverse position using LOBL strategy,then select the better one 10:End For 11:Evaluate the fitness values of all gorillas 12:Set the best solution as a silverback Xsilverback 13:For each gorilla do //Exploitation stage 14:If C ≥W then 15:Update the position of current gorilla according to Eq.(5)16:Else 17:Update the position of current gorilla according to Eq.(7)18:End If 19:End For 20:Update the fitness values of all gorillas 21:Update the global optimal solution Xsilverback 22:Perform AβHC strategy for the global optimal solution Xsilverback 23: t=t+1 24:End While 25:Output the global best solution Xsilverback and its fitness value

4 Experimental Results and Discussion

In this section,a total of 19 benchmark functions from the literature[64]are selected for contrast experiments to comprehensively evaluate the feasibility and effectiveness of the proposed IGTO algorithm.First,the definitions of these benchmark functions,parameter settings,and measurements of algorithm performance are presented.Afterwards,the basic GTO and other five advanced meta-heuristic algorithms,such as GWO[65],WOA[29],SSA[66],HHO[33],and SMA[36],are employed as competitors to validate the improvements and superiority of the proposed algorithm based on the solution accuracy,boxplot,convergence behavior,average computation time,and statistical result.Final,the scalability of IGTO is investigated by solving high dimensional problems.All the simulation experiments are implemented in MATLAB R2014b with Microsoft Windows 7 system,and the hardware platform of the computer is configured as Intel(R)Core(TM)i5-7400 CPU @ 3.00 GHz,and 8 GB of RAM.

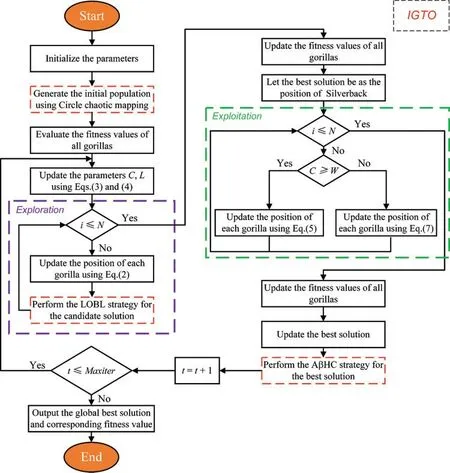
Figure 4:Flowchart of the proposed IGTO algorithm

4.1 Benchmark Function

The benchmark functions used in this paper could be divided into three various categories:unimodal(UM),multimodal(MM),and fix-dimension multimodal(FM).The unimodal functions(F1～F7)contain only one global minimum,which are frequently used to detect the development competence and convergence rate of algorithms.The multimodal functions(F8～F13),consisting of several local minima and a single global optimum in the search space,are well suited for assessing the algorithm’s capability to explore and escape from local optima.The fix-dimension multimodal functions(F14～F19)are combinations of the previous two forms of functions,but with lower dimensions,and they are designed to evaluate the stability of the algorithm.Table 1 shows the formulations,spatial dimensions,search ranges,and theoretical minimum of these functions.In addition,3D images for the search space of several typical functions are displayed in Fig.5.

Table 1:Benchmark functions

Table 1(continued)TypeFunctionDimRangeFmin FMF14(x)=( 1 500+25∑j=1(j+n∑i=1(xi-aij)6)-1)-12[-65,65]0.998 F15(x)=11∑i=1[ai- x1(b2i+bix2)b2i+bix3+x4]24[-5,5]0.00030 F16(x)=4x21-2.1x41+ 1 3x61+x1x2-4x22+4x422[-5,5]-1.0316 F17(x)=-4∑i=1 ci exp(-3∑j=1 aij(xj-pij)2)3[1,3]-3.86 F18(x)=-4∑i=1 ci exp(-6∑j=1 aij(xj-pij)2)6[0,1]-3.32 F19(x)=-10∑i=1[(X-ai)(X-ai)T+ci]-14[0,10]-10.5363

Figure 5:Search space of typical benchmark functions in 3D

4.2 Parameter Setting

In order to estimate the performance of the improved IGTO algorithm in solving global optimization problems,we select the basic GTO[54]and five state-of-the-art algorithms,namely GWO[65],WOA[29],SSA[66],HHO[33],and SMA[36].For fair comparisons,the maximum iteration and population size of seven algorithms are set as 500 and 30,respectively.As per the references[9,61]and extensive trials,in the proposed IGTO algorithm,we set the scale factorn=12000,K=30,βmax=1 andβmin=0.1.Besides,all parameter values of the remaining six algorithms are set the same as those recommended in the original papers,as shown in Table 2.These parameter settings assure the fairness of the comparison experiments by allowing each algorithm to make the most of its optimization property.All algorithms are executed independently 30 times within each benchmark function to decrease accidental error.

Table 2:Parameter setting of the optimization algorithms

4.3 Evaluation Criteria of Performance

In this study,two metrics are used to measure the performance of the proposed algorithm including the average fitness value(Avg)and standard deviation(Std)of optimization results.The average fitness value intuitively characterizes the convergence accuracy and the search capability of the algorithm,which is calculated as follows:

wherendenotes the times that an algorithm has run,andSiindicates the obtained result of each operation.

And the standard deviation indicates the deviation degree between the experimental results and the average value.The equation of standard deviation is available as follows:

4.4 Comparison with IGTO and Other Algorithms

In this subsection,to examine the performance of the proposed algorithm,IGTO is compared with the basic GTO and five other advanced algorithms according to benchmark function optimization results.For fair comparisons,the maximum iteration and population size of seven algorithms are set as 500 and 30,respectively,and the rest parameter settings have been given in Subsection 4.2 above.Meanwhile,each algorithm runs 30 times independently on the test functionF1-F19in Table 1 to decrease random error.The average fitness value(Avg)and standard deviation(Std)of each algorithm obtained from the experiment are reported in Table 3.In general,the closer the average fitness(Avg)to the theoretical minimum,the higher convergence accuracy of the algorithm.While the smaller the value of the standard deviation(Std),the better the stability and robustness of the algorithm.

As seen from Table 3,when solving the unimodal benchmark functions(F1～F7),IGTO obtains the global optimal minima with regard to the average fitness on functionsF1～F4.For functionF5,the convergence accuracy of IGTO has a great improvement over its predecessors GTO and it is the winner among all algorithms.For test functionF6,the results of IGTO are similar to SSA and GTO,yet still marginally better them.Besides,IGTO shows superior results on functionF7in contrast to other optimizers.In terms of standard deviation,the proposed IGTO has excellent performance on all test problems.Given the properties of the unimodal functions,these results show that IGTO has outstanding search precision and local exploitation potential.

Table 3:Comparison results of different algorithms on 19 benchmark functions

The multimodal benchmark functions(F8～F13)have many local minima in the search space,so these functions are usually employed to analyze the algorithm’s potential to avoid the local optima.For functionsF8,F12andF13,the average fitness and standard deviation of IGTO are obviously better than the rest of the algorithms.For functionF9,IGTO obtains the same global optimal minima as WOA,HHO,SMA,GTO.Moreover,HHO,SMA,GTO and IGTO obtains the same performance on functionsF10andF11.It hopefully validates that the proposed IGTO can effectively bypass the local optimum and find high quality solutions.

The fix-dimension multimodal functions(F14～F19)consist of few local optima,which are designed to evaluate the stability of the algorithm in switching between exploration and exploitation processes.As far as the average fitness values are concerned,IGTO performs the same as SMA and GTO on functionF14,albeit better than others.For functionsF15,F18andF19,IGTO can generate superior results to all competitors.For functionF16,the performance of seven optimizers is identical.Although the result of the proposed IGTO is worse than HHO on functionF17,it still ranks second and shows significant improvements over the basic GTO to a certain extent.On the other hand,IGTO achieves the optimal standard deviation on all test cases.This proves that our proposed IGTO is able to keep a better balance between exploration and exploitation.

In view of the above,a summary can be drawn that the proposed multi-strategy combination IGTO algorithm exhibits strong global search capability and is superior to the other six intelligent algorithms in comparison.Benefiting from the hybrid AβHC with GTO operation,the solution precision of IGTO is greatly strengthened.At the same time,LOBL strategy is effective to expand the unknown search area and avoid the algorithm falling into the local optima.

In order to better illustrate the stability of the proposed algorithm,the corresponding boxplots of functions 1,2,3,5 and 6 from UM benchmark functions,functions 9,10 and 12 from MM benchmark functions,and function 15 selected from FM benchmark functions are shown in Fig.6.From Fig.6,it can be seen that IGTO algorithm shows remarkable consistency in most issues with respect to the median,maximum and minimum values compared with the others.In addition,IGTO generates no outliers during the iterations with the more concentrated distribution of convergence values,thereby verifying the strong robustness and superiority of the improved IGTO.

Fig.7 visualizes the convergence curves of different algorithms on nine representative benchmark functions.Likewise,where functions 1,2,3,5 and 6 are unimodal,functions 9,10 and 12 are multimodal,and function 15 belongs to the fix-dimension multimodal category.From Fig.7,it is clear that the convergence speed of IGTO is the fastest among all algorithms on functionsF1～F3,and the proposed algorithm can rapidly reach the global optimal solution at the beginning of the search process.For functionsF5andF6,IGTO has a similar trend to HHO and GTO in the initial stage,but its efficiency is fully demonstrated in the late iterations,and eventually the proposed IGTO obtains the best result.For functionsF9,IGTO remains a superior convergence rate and obtains the global optimum within 20 iterations.Although the convergence accuracy of IGTO is the same as that of HHO,SMA and the basic GTO on functionsF10,yet it converges more quickly.For functionF12,the proposed algorithm is still the champion compared with the remaining six optimizers in terms of final accuracy and speed.Besides,the convergence curves of seven algorithms are pretty close on the fix-dimension multimodal functionF15.However,the performance of IGTO is slightly better than the others.

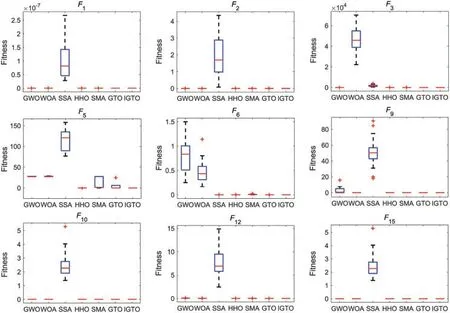
Figure 6:Boxplot analysis of different algorithms on partial benchmark functions

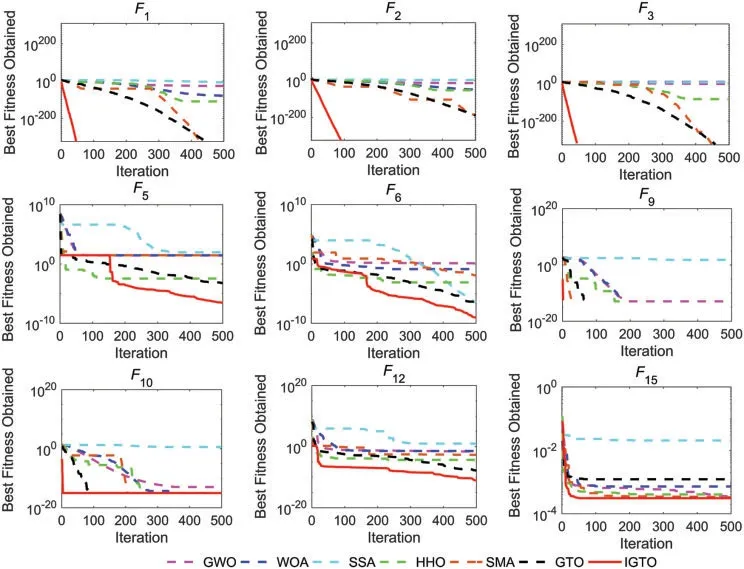
Figure 7:Convergence curves of different algorithms on nine benchmark functions

On the basis of experimental results of boxplot analysis and convergence curves,IGTO has a considerable enhancement in convergence speed and stability compared with the basic GTO,which is owed to the good foundation of global search laid by Circle chaotic mapping and LOBL strategy.

The average computation time spent by each algorithm on test functionsF1～F19is reported in Table 4.For a more intuitive conclusion,the total runtime of each method is calculated and ranked as follows:SMA(14.118 s)＞IGTO(8.073 s)＞GTO(6.690 s)＞HHO(6.568 s)＞GWO(4.912 s)＞SSA(4.897 s)＞WOA(4.065 s).It can be found that IGTO uses more computation time than GTO,which is the second to last.Compared with the basic GTO algorithm,the introduction of three improved strategies increases the steps of the algorithm and extra time.Of course,the high computation cost of GTO algorithm itself is also a primary cause of this.However,the IGTO takes less time than SMA on most test functions.To improve the solution accuracy,a little more runtime is sacrificed.On the whole,the proposed algorithm is acceptable in view of the optimal search performance,and its limitation is still the need to decrease the computational time.

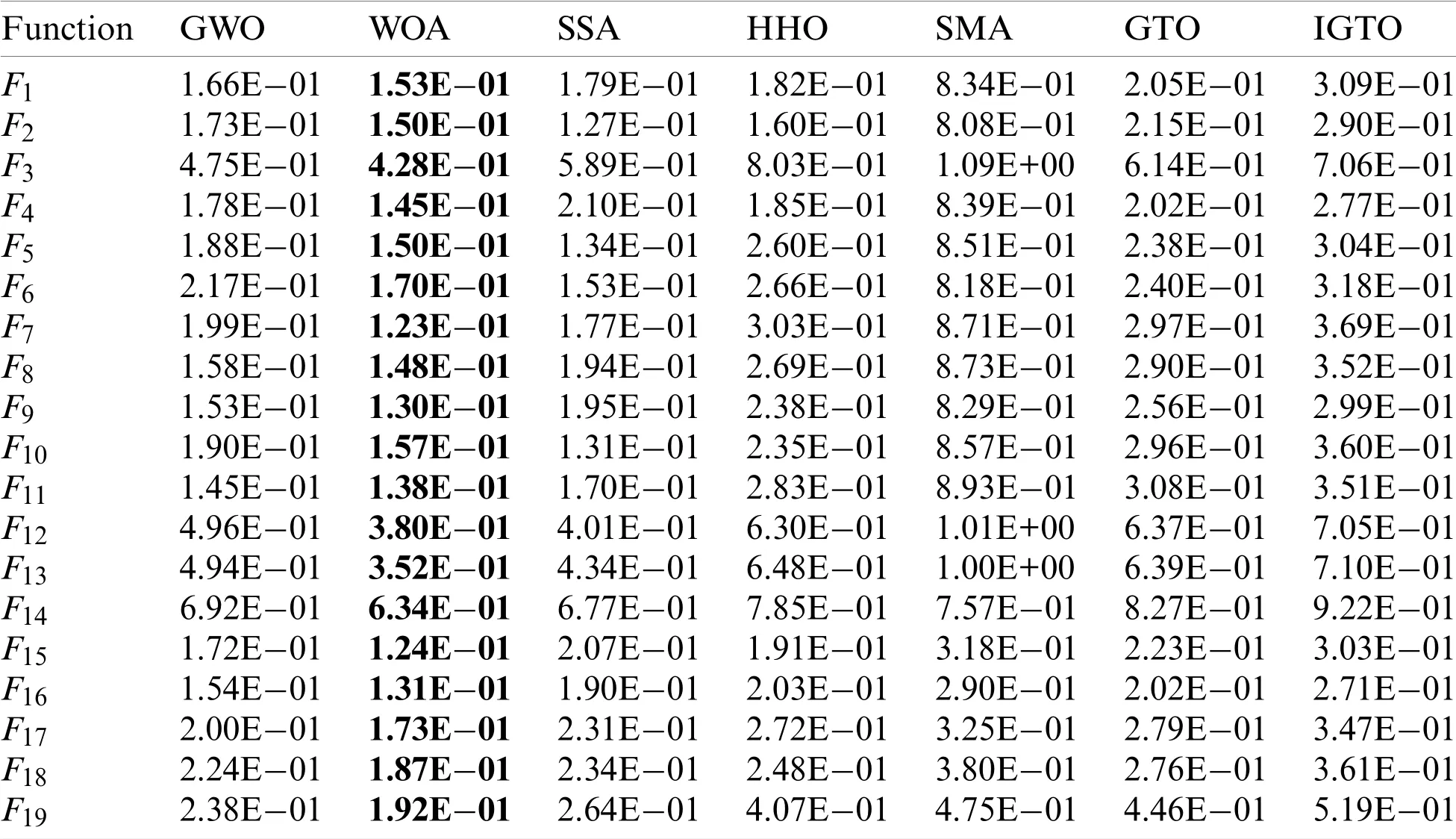
Table 4:Comparison results of the average computation time of different algorithms(unit:s)

Moreover,since the average fitness(Avg)and standard deviation(Std)of the algorithm after 30 runs are not compared with the results of each run,it is often not accurate to evaluate the performance of an algorithm based only on the mean and standard deviation.To represent the robustness and fairness of the improved algorithm,the Wilcoxon rank-sum test[67],a nonparametric statistical test approach is used to estimate the significant differences between IGTO and other algorithms.For Wilcoxon rank-sum test,the significance level is set to 0.05 and acquiredp-values are listed in Table 5.In this table,the sign “+” denotes that IGTO performs significantly better than the corresponding algorithm,“=”denotes that the performance of IGTO is analogous to that of the compared algorithm,“-” denotes that IGTO is poorer than the compared one,and the last line counts the total number of all signs.It can be seen from the table that for the 19 benchmark test functions,the proposed IGTO algorithm outperforms GWO on 19 functions,WOA and SSA on 18 functions,HHO on 16 functions,SMA on 14 functions,and the basic GTO on 13 functions,respectively.Therefore,according to the statistical theory analysis,our proposed IGTO has a significant enhancement over the other algorithms and it is the optimal optimizer among them.

Table 5:Statistical results of IGTO on Wilcoxon rank-sum test

Lastly,the mean absolute error(MAE)of all algorithms on 19 benchmark problems is evaluated and ranked.MAE is also a useful statistical tool to reveal the gap between the experimental results and the theoretical values[1],and its mathematical expression is as follows:

In Eq.(23),Nis the number of benchmark functions used,oirepresents the desired value of each test function,andaiis the actual value obtained.The MAE and relative rankings of each algorithm are reported in Table 6.From this table,it is obvious that IGTO outperforms all competitors and the MAE of IGTO is reduced by 2 orders of magnitude compared to GTO,which once again demonstrates the superiority of the proposed algorithm statistically.

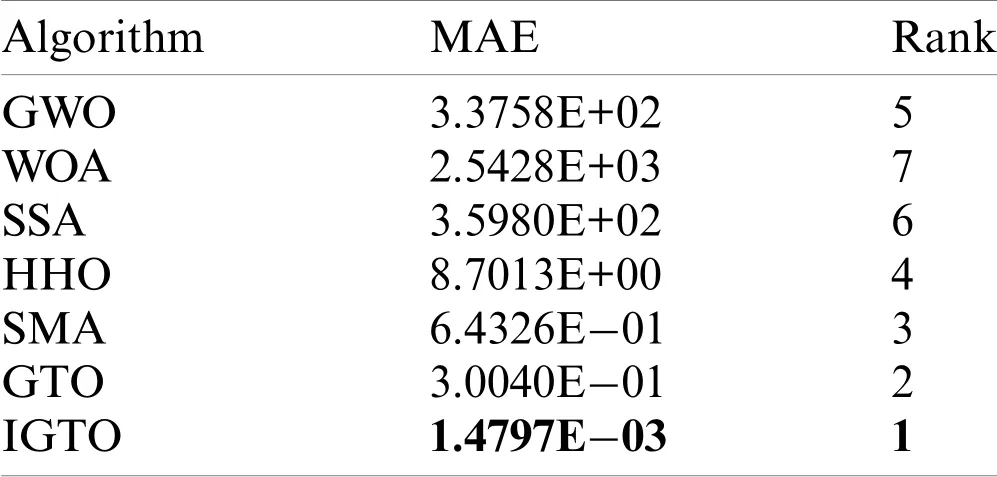
Table 6:Ranking of different algorithms by MAE on 19 benchmark functions

4.5 Scalability Test

Scalability reflects the execution efficiency of an algorithm in different dimensional spaces.As the dimensions of the optimization problem increase,most current intelligent algorithms are highly prone to be ineffective and subject to “dimensional disaster”.To investigate the scalability of IGTO,the proposed algorithm is utilized to optimize 13 benchmark functionsF1～F13in Table 1 with higher dimensions(i.e.,50,100 and 200 dimensions).The average fitness values(Avg)obtained by the basic GTO and IGTO on each function are reported in Table 7.From the data in the table,it is clear that the convergence accuracy of both algorithms gradually decreases with the increase in dimensions,which is due to the fact that the larger the dimensions,the more elements an algorithm needs to optimize.However,the experimental results of IGTO are consistently superior to GTO on functionsF1～F8,F12andF13,and the disparity in optimization performance between them is increasingly obvious as the dimension increases.Besides,it is notable that the proposed IGTO can always obtain the theoretical optimal solution on functionsF1～F4.For functionsF9～F11,two algorithms obtain the same performance.

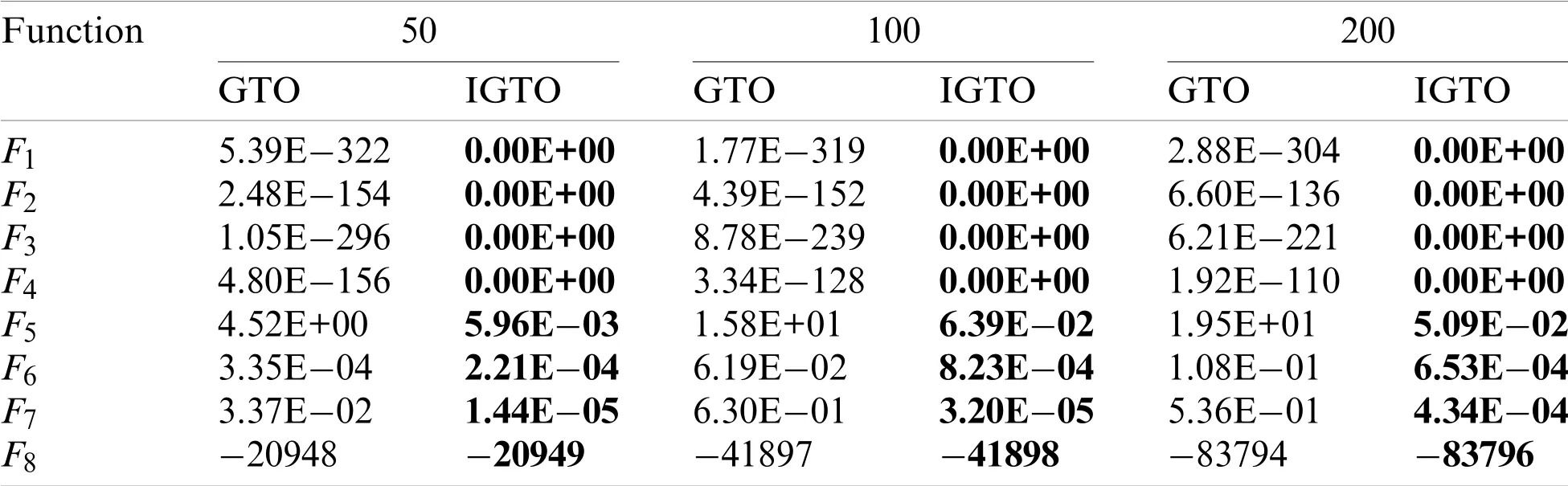
Table 7:Fitness values of GTO and IGTO in 50,100,200 dimensions on 13 test functions

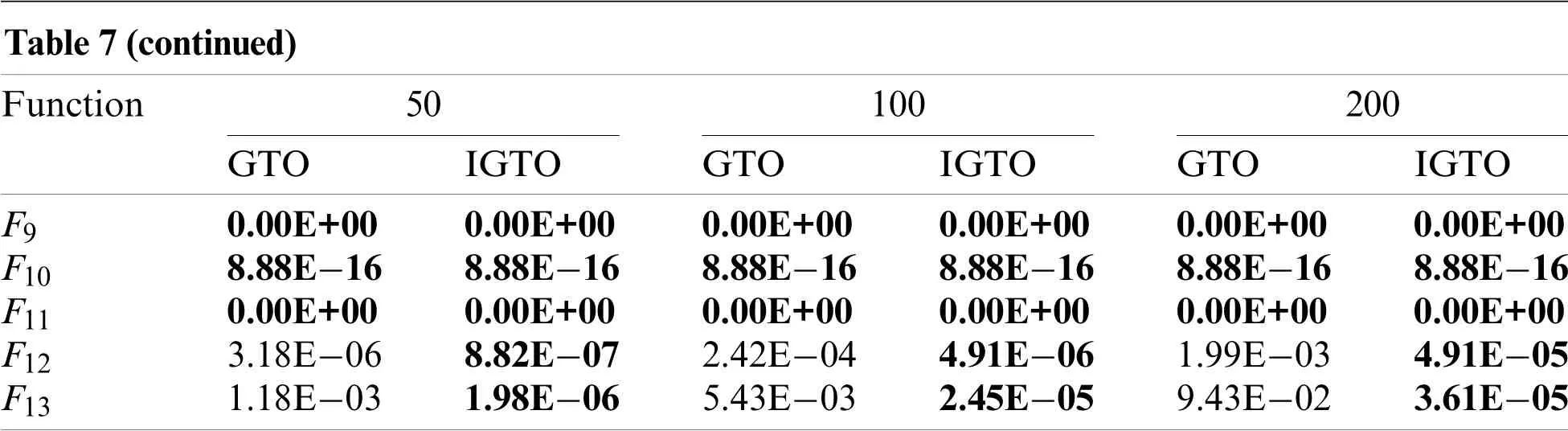
Note:The best result obtained is highlighted in bold.

The overall results fully prove that IGTO is not only able to solve low-dimensional functions at ease,but also maintain good scalability in high-dimensional functions,that is to say,the performance of IGTO does not deteriorate significantly when tackling high-dimensional problems,and it can still provide high-quality solutions effectively with well exploitation and exploration capabilities.

5 IGTO for Solving Engineering Design Problems

In this section,the applicability of the proposed IGTO is tested by solving four practical engineering design problems including pressure vessel design problem,gear train design problem,welded beam design problem and rolling element bearing design problem.For the sake of convenience,the death penalty[68]function is used here to handle the infeasible solutions subjected to constraints.IGTO runs independently 30 times for each issue,with the maximum iterations and population size are set to 500 and 30,respectively.At last,the obtained results are compared against those of different advanced meta-heuristic algorithms in the literature,as well as the corresponding analysis are presented.

5.1 Pressure Vessel Design

The pressure vessel design problem was first purposed by Kannan et al.[69],the purpose of which is to minimize the overall fabrication cost of a pressure vessel.There are four decision variables involved in this optimum design:Ts(z1,thickness of the shell),Th(z2,thickness of the head),R(z3,inner radius),andL(z4,length of the cylindrical portion).Fig.8 illustrates the structure of pressure vessel used in this study and its related mathematical model can be defined as follows:

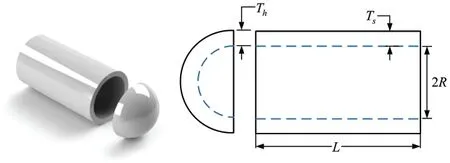
Figure 8:Pressure vessel design problem

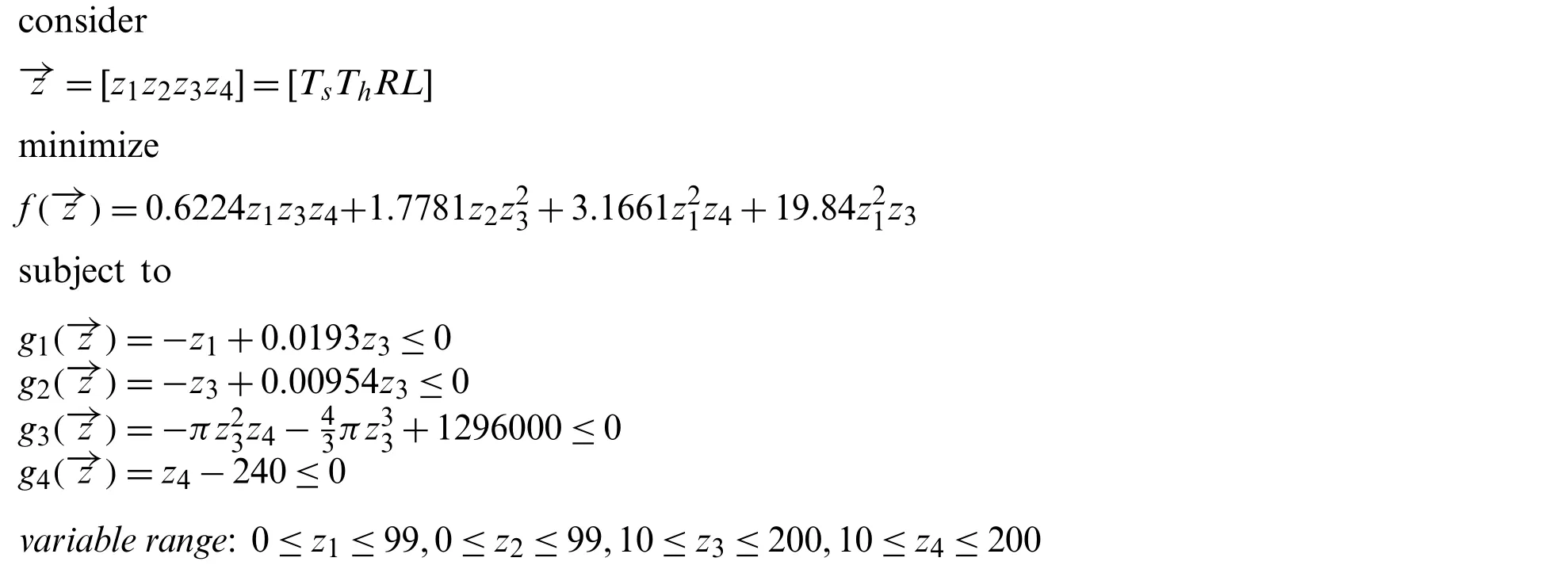
The experimental results of IGTO for this problem are compared against those resolved by GTO,SMA[36],HHO[33],AOA[4],SSA,WOA[29],and GWO[65],as shown in Table 8.It is shown that IGTO can provide the best design among all algorithms,and the minimum cost obtained isf(→z)min=5904.2189,which corresponds to the optimum solution→z=[0.7889 0.3900 40.8764 192.4031].Thus,the proposed IGTO algorithm is regarded as more suitable for solving such problem.

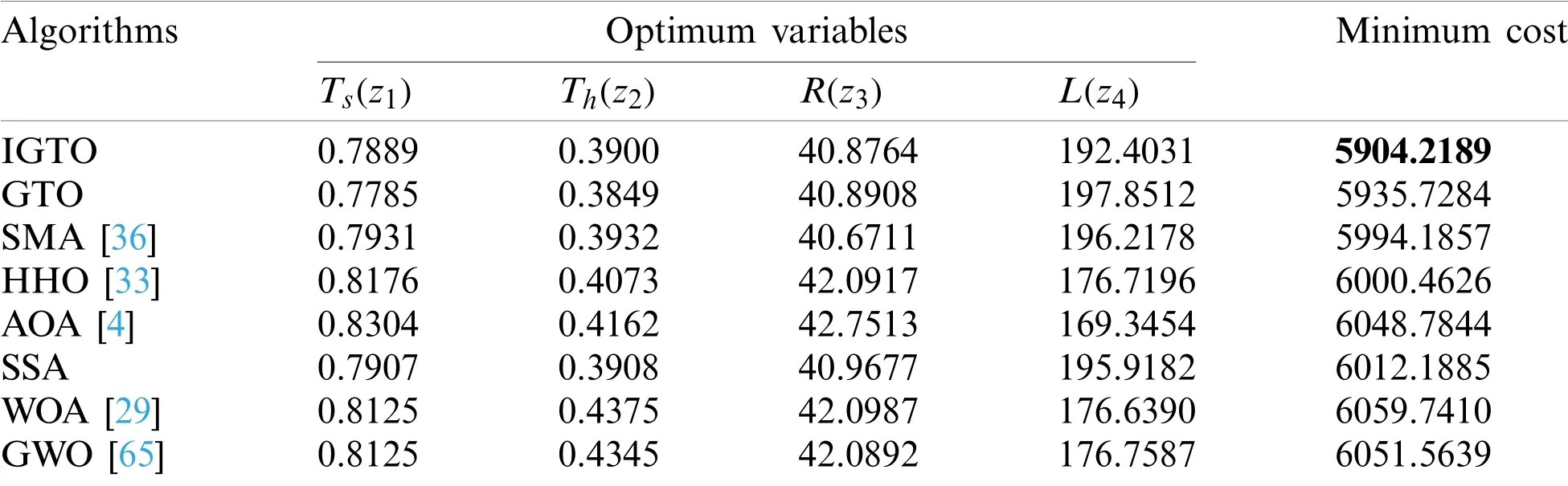
Table 8:Comparison results of pressure vessel design

5.2 Gear Train Design

This is a classical mechanical engineering problem developed by Sandgren[70].Fig.9 shows the schematic view of the gear train.As its name suggests,the ultimate aim of this problem is to find four optimal parameters that minimize the gear ratioas much as possible.The test case can be also represented mathematically as follows:

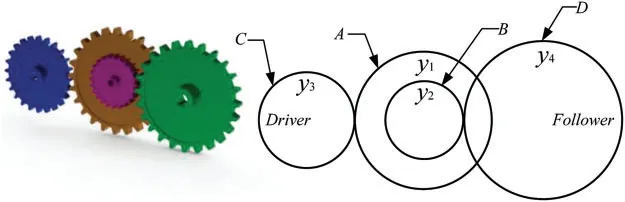
Figure 9:Gear train design problem

Table 9 reports the detailed results of comparative experiments for the gear train design problem.From the data in Table 9,it is apparent that the proposed IGTO is better than other optimizers in handling this case and effectively finds a brilliant solution.

Table 9:Comparison results of gear train design

5.3 Welded Beam Design

As its name implies,the purpose of this welded beam design problem is to reduce the total manufacturing cost as much as possible.This optimum design contains four decision parameters:the width of weld(h),the length of the clamped bar(l),the height of the bar(t),and the bar thickness(b).Besides,in the optimization process,several constraints should not be contravened such as bending stress in the beam,buckling load,shear stress and end deflection.The schematic view of this issue is shown in Fig.10,and the related mathematical formulation is illustrated as follows:consider

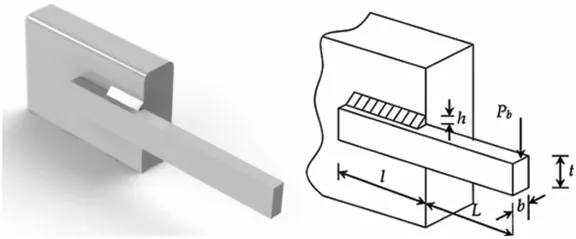
Figure 10:Welded beam design problem

The optimal results of IGTOvs.those achieved by GTO,MVO[21],SSA[66],HHO[33],WOA[29],MTDE[71],ESSWOA[9]are reported in Table 10.As can be seen from Table 10,it is obvious that the proposed IGTO provides better design than majority of other algorithms.The minimum costis obtained with the related optimal solutionTherefore,it is justifiable to believe that the proposed IGTO has the superior capability to deal with such problem.

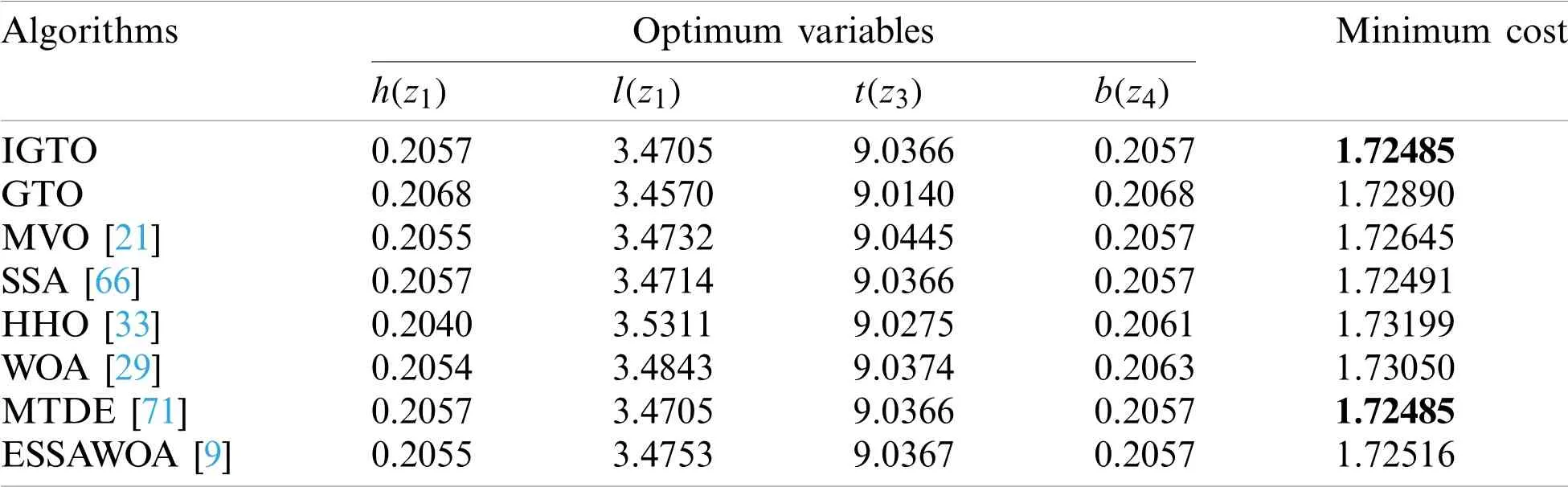
Table 10:Comparison results of welded beam design

5.4 Rolling Element Bearing Design

Unlike the previous problems,the final objective of this issue is to maximize the dynamic load capacity of rolling element bearings as possible.The structure of a rolling element bearing is illustrated in Fig.11.There is a total of ten structural variables involved in the solution of this optimization problem,namely:pitch diameter(Dm),ball diameter(Db),the number of balls(Z),the inner and outer raceway curvature radius coefficient(fiandfo),Kdmin,Kdmax,δ,eas well asζ.Mathematically,the description of this problem is given as follows:

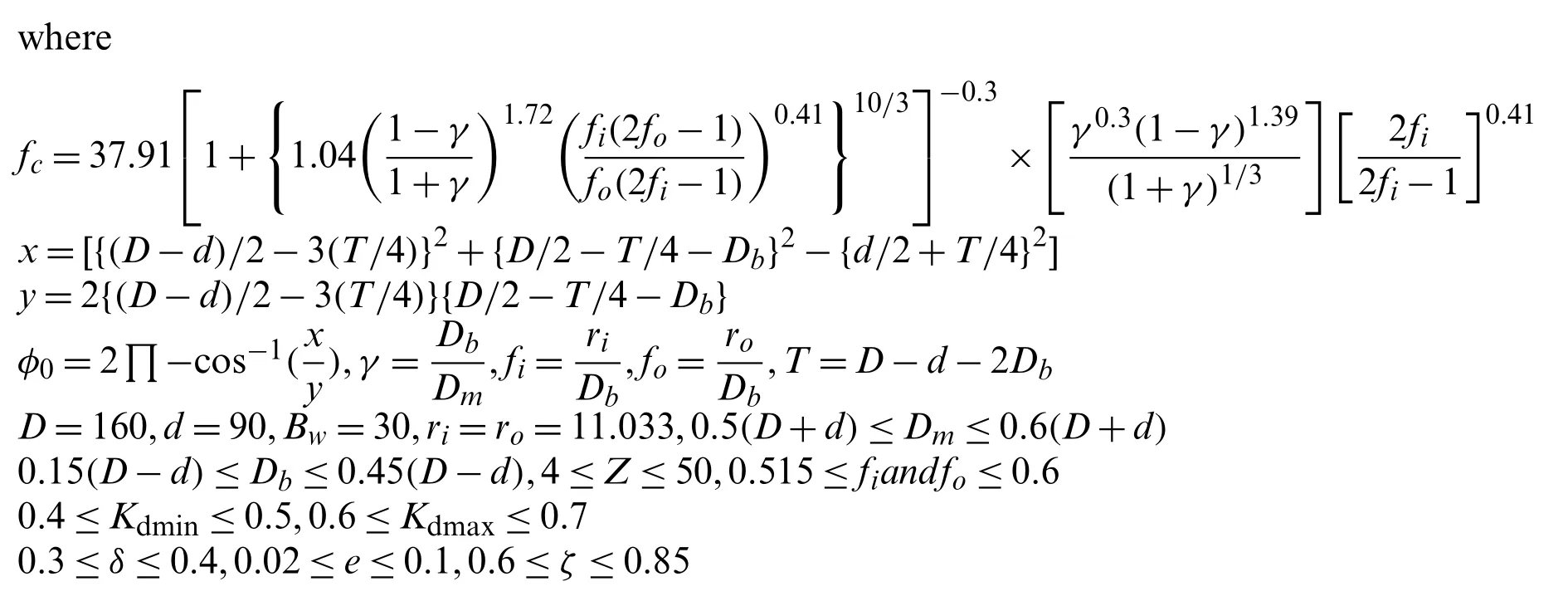
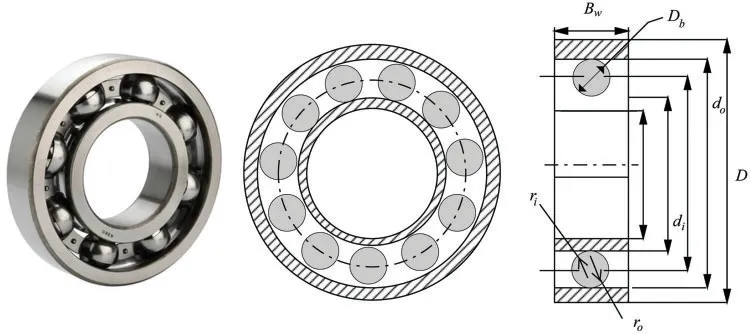
Figure 11:Rolling element bearing design problem

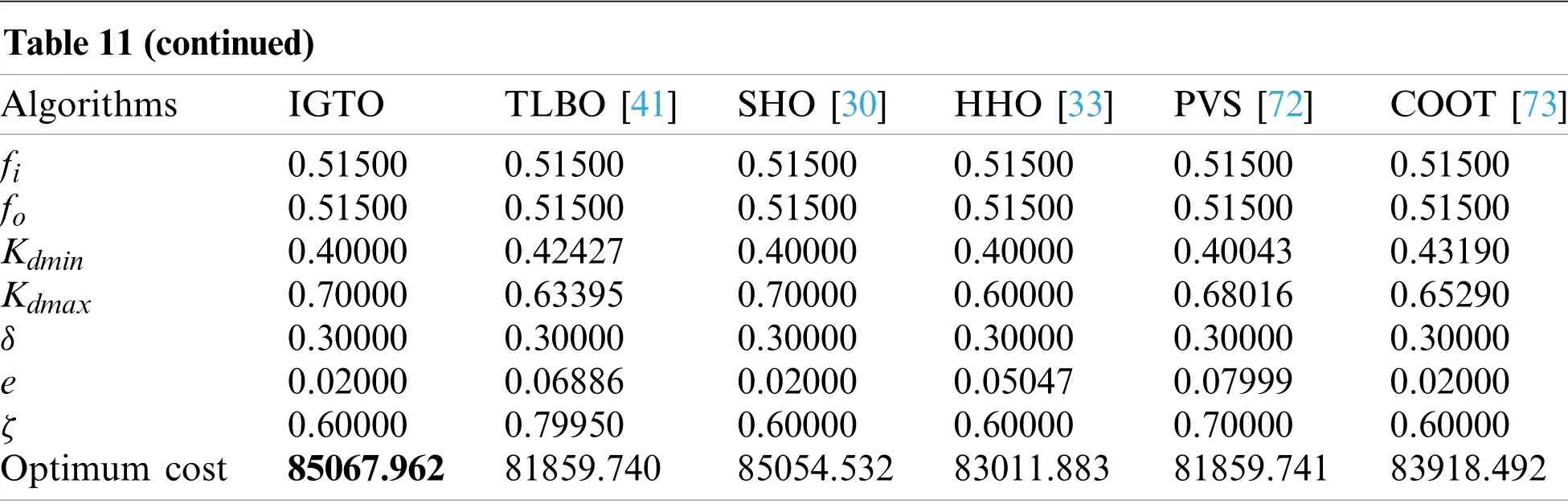
The results of optimum variables and fitness fetched applying different intelligent algorithms are listed in Table 11.Compared with other well-known optimizers,the proposed IGTO reveals the superior quality solution atcorresponding to the best fitnessCd=85067.962 with a significant improvement.This case once again highlights the applicability of IGTO algorithm.

Table 11:Comparison results of rolling element bearing design

Note:The best solution obtained is highlighted in bold.

As a summary,it is reasonable to believe that the proposed IGTO is equally feasible and competitive in practical engineering design problems from the observed results.In addition,the excellent performance in resolving engineering design problems indicates that IGTO is able to be widely used in real-world optimization problems as well.

6 IGTO for Training Multilayer Perceptron

Multilayer perceptron(MLP),as one of the most extensively used artificial neural network models[74],has been successfully implemented for solving various real-world issues such as pattern classification[75]and regression analysis[76].The MLP is characterized by multiple perceptron,in which there is at least one hidden layer in addition to one input layer and one output layer.The information is received as input on one side of the MLP and the output is supplied from the other side via one-way transmission between nodes in different layers.For the MLP,since the sample data space is mostly high-dimensional and multimodal,at the same time there is also a potential for data interference by noise,data redundancy and data loss.Thus,the main purpose of training the MLP is to update two crucial parameters that dominate the final output:the weightsWand biasesθ,which is a very challenging optimization problem[15,77].In this section,the Balloon and Breast cancer datasets from the University of California at Irvine(UCI)repository[78]are utilized for examining the applicability of the proposed IGTO algorithm for training MLP.Table 12 presents the specification of these datasets.

Table 12:Specification of the datasets

In order to measure the algorithm performance of training the MLP,the average mean square error criteriafor all training samples are defined as follows:

In Eq.(24),qrepresents the number of training samples,mis the number of outputs,andanddenote the desired and actual output fori-th input withk-th training sample is used,respectively.If the actual output data is closer to the desired one,the value ofis smaller,which means that the trained model gains a better performance.

Besides the optimization algorithms shown in Table 2,Tunicate Swarm Algorithm(TSA)[34],Sooty Tern Optimization Algorithm(STOA)[35],and Seagull Optimization Algorithm(SOA)[32]are also taken into account in this experiment.The variables are assumed to be in the range of[-10,10].Each optimizer executes independently 10 times,with the maximum iterations and population size are set to 250 and 30,respectively.Meanwhile,the parameters of all algorithms are consistent with the original literature.With regard to the structure of the MLP,the number of nodes in the hidden layer is equal to 2n+1 as recommended in[74],wherendenotes the number of attributes in the dataset.Fig.12 illustrates an example for the process of training the MLP by IGTO.value of

Figure 12:Training MLP by the proposed IGTO

Table 13:Comparison results of two datasets

All these results demonstrate that the proposed algorithm has a stable and consistent ability to get rid of the local optimum and eventually find the global minima in the complex search space.Besides,this case also highlights the applicability of IGTO algorithm.IGTO is capable of finding more suitable crucial parameters for MLP,thus making it perform better.

7 Conclusion and Future Work

In this paper,a novel improved version of the basic gorilla troops algorithm named IGTO was put forward to solve complex global optimization problems.First,Circle chaotic mapping was introduced to enhance the diversity of the initial gorilla population.Second,the lens oppositionbased learning strategy was adopted to expand the search domain,thus avoiding the algorithm falling into the local optima.Moreover,the adaptive β-hill climbing algorithm was hybridized with GTO to boost the quality of final solutions.In order to evaluate the effectiveness of the proposed algorithm,IGTO was compared with the basic GTO and five other state-of-the-art algorithms based on 19 classical benchmark functions,including unimodal,multimodal,and fix-dimension multimodal functions.Besides,the non-parametric Wilcoxon’s rank-sum test and average absolute error(MAE)were used to analyze the experimental results.The statistical results demonstrate that the proposed IGTO algorithm provides better local optimum avoidance,solution quality,and robustness than the other competitors.Three improvements can significantly boost the performance of IGTO.In order to further test the applicability of IGTO in real-world applications,IGTO was applied to solve four engineering design problems and train multilayer perceptron.The experimental results show that IGTO has strong competitive performance in terms of optimization accuracy.

Nevertheless,as mentioned in the experiment section above,IGTO still has the main limitation of high computation time,which needs to be improved.It is believed that this situation could be mitigated via the introduction of several parallel mechanisms,e.g.,master-slave model,cell model and coordination strategy.

In the future work,we will aim to further enhance the solution accuracy of IGTO while reducing the total process consumption.Also,we plan to further investigate the impact of the lens opposition-based learning and adaptive β-climbing strategies on the performance of other meta-heuristic algorithms.In addition,we hope to apply the proposed technique to solve more practical problems,such as the parameter self-tuning of speed proportional integral differential(PID)controller for brushless direct current motors,the global path planning for autonomous underwater vehicles in a complex environment,and the maximum power point tracking of solar photovoltaic systems.

Acknowledgement:The authors are grateful to the editor and reviewers for their constructive comments and suggestions,which have improved the presentation.

Funding Statement:This work is financially supported by the Fundamental Research Funds for the Central Universities under Grant 2572014BB06.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.