Modeling the Spread of Tuberculosis with Piecewise Differential Operators

Abdon Atangana and Ilknur Koca

1Institute for Groundwater Studies,Faculty of Natural and Agricultural Sciences,University of the Free State,Bloemfontein,9301,South Africa

2Department of Medical Research,China Medical University Hospital,China Medical University,Taichung,008864,Taiwan

3Department of Accounting and Financial Management,Seydikemer High School of Applied Sciences,Mugla Sitki Kocman University,Mugla,48300,Turkey

ABSTRACT Very recently,a new concept was introduced to capture crossover behaviors that exhibit changes in patterns.The aim was to model real-world problems exhibiting crossover from one process to another,for example,randomness to a power law.The concept was called piecewise calculus,as differential and integral operators are defined piece wisely.These behaviors have been observed in the spread of several infectious diseases,for example,tuberculosis.Therefore,in this paper,we aim at modeling the spread of tuberculosis using the concept of piecewise modeling.Several cases are considered,conditions under which the unique system solution is obtained are presented in detail.Numerical simulations are performed with different values of fractional orders and density of randomness.

KEYWORDS Spread of tuberculosis;piecewise differentiation;numerical simulation

1 Introduction

Although several studies have been done on behaviors of the tuberculosis virus,its spread,and its effect on the human’s body until today,this virus persists and kills humans around the world each year.It is even believed that the tuberculosis virus has affected about 25 percent of the world population since about one percent of the world population is infected each year according to what is reported in the literatures[1–4].Tuberculosis is a seasonal transmissible disease,as the peaks are reached every spring and summer.However,there is no apparent scientific reason recorded that can explain this variation.Nevertheless,it is recorded that the virus spreads more during weather conditions like low temperature,humidity,and low rainfall.Thus tuberculosis incidence rates could be linked to change in the climate.Having peaks that occurred during some period of the year show that the spread had many waves since antiquity.Indeed,each wave has a specific pattern different from others or similar in some cases.It can be concluded that the virus spread follows piecewise patterns.Mathematicians have tried to provide mathematical models to depict the spread behaviors as a function of time.Several studies have been performed in the decades.The reproductive number of this virus has been calculated in many studies.New and modified models have been provided and studied in detail.Several differential and integral operators have been used,for example,fractional differential operators to replicate spread behaviors.Fractional derivative based on power law was introduced to replicate behaviors resembling the power law[5–11].Different techniques have been employed,for example,the stochastic process to capture random behaviors.Nevertheless,the problem of different was not really addressed.The concept of piecewise differential and integral operators was recently suggested and employed to model some complex real-world problems,such as chaos and other epidemiological problems[12].The concept seems to be efficient when modeling problems with crossover behaviors.In this paper,we aim to modify an existing tuberculosis model with the concept of piecewise differentiation.

1.1 Important Definitions of Fractional Modelling

Definition 1:Letα ＞0 of a functionh:(0,∞)→Rand the Riemann-Liouville derivative of fractional order is presented as

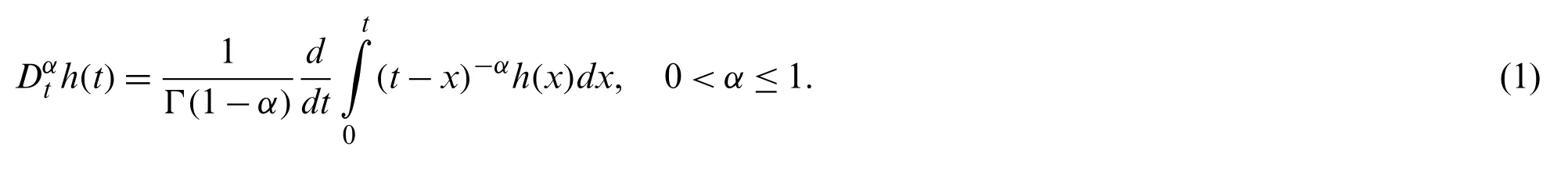
Definition 2:Leth:H1(a,b),b ＞a,0＜α ＜1 then,the Caputo-Fabrizio derivative of fractional derivative is presented as

Definition 3:Leth:H1(a,b),b ＞a,α∈(0,1)then,the definition of the new fractional derivative(Atangana-Baleanu derivative in Caputo sense)is presented as

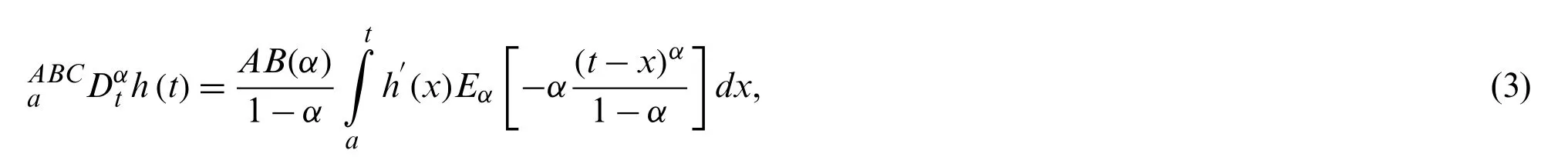
is a normalization function.

Definition 4:Lethbe continuous not necessary differentiable in[t1,T].Thus,the piecewise Riemann-Liouville derivative is presented as

Definition 5:The piecewise derivative with classical and exponential decay kernel is defined as

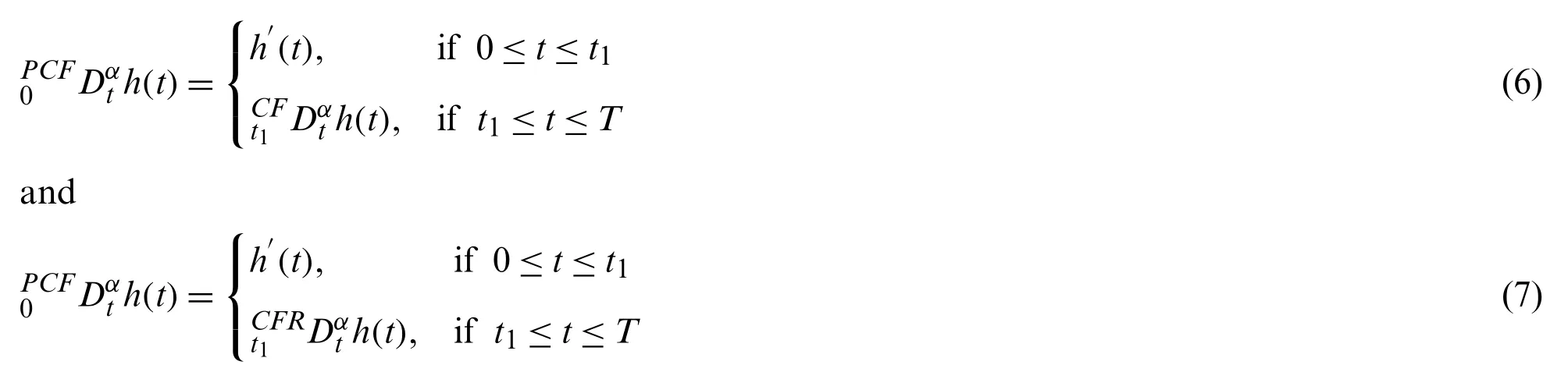
Definition 6:The piecewise derivative with classical and Mittag-Leffler kernel is given as

Definition 7:Lethbe continuous andα ＞0 then a piecewise integral ofhis given as

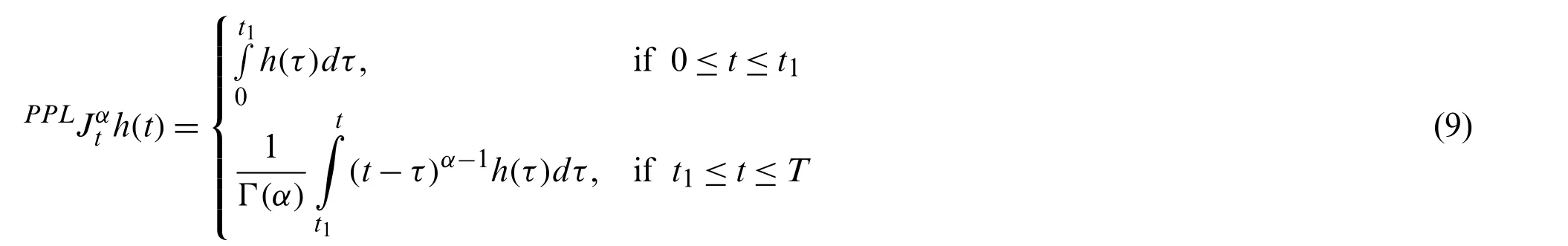
Definition 8:Lethbe continuous andα ＞0 then a piecewise integral ofhis given as

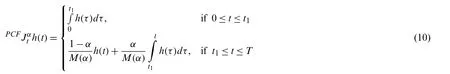
2 Tuberculosis Epidemic Model

In this section,we take into account the following piecewise model of tuberculosis:

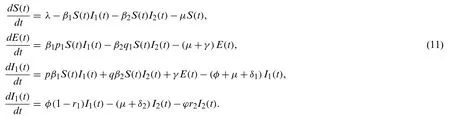
The initial conditions are taken as follows:

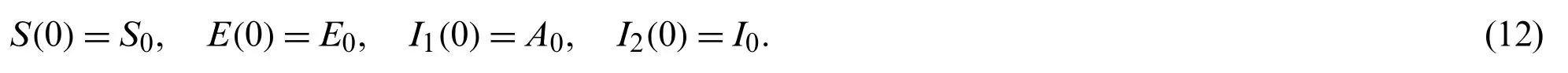
But we noted that the model was considered with its classical version in paper[13]before.Now,we give the meanings of the parameters of model considered in this paper given by Table 1 below:

Table 1:The meanings of the parameters of model

2.1 Second Derivative of Lyapunov Function and Strength Number

Lyapunov function formulation has been used in different analyses in different fields in the last past year.In epidemiology,this function has been used to determine the stability analysis of an epidemiological model.It has been reported that the Lyaponuv can be viewed as energy;therefore,a sign of the first derivative of the function can be useful for the determination of stability.Nevertheless,the sign of the first derivative of a function may not be enough to define whether we have a local maximum or local minimum.On this note,it was suggested that the sign of the second derivative should also be studied.In this section,we shall proceed with such analysis to determine the sign of our model’s second derivative of the associate Lyaponuv function.

In this section,we present the second derivative of Lyapunov function for the model[2–14].

Now we find second derivative of Lyapunov function for model with following equality:

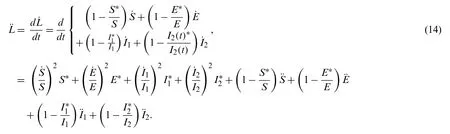
Here second derivatives of classes are given as below:

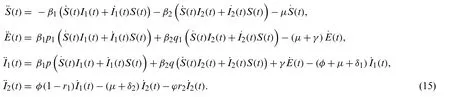
Then we have

where

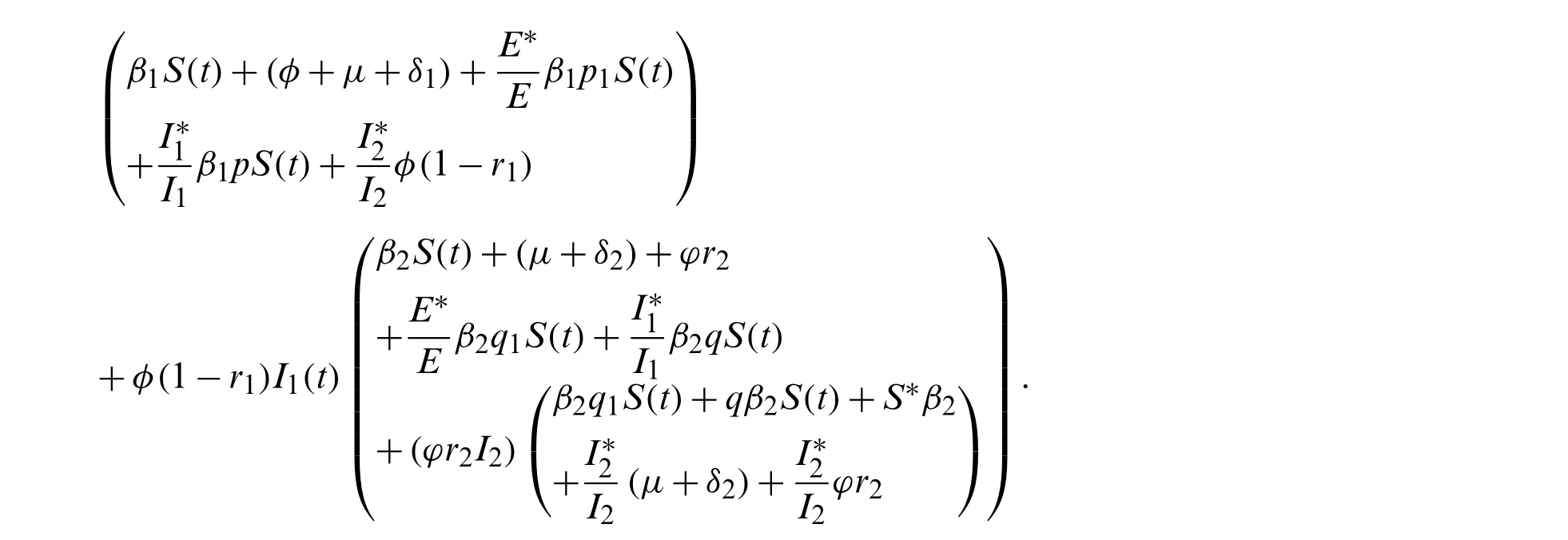
Now we can easly put following results for obtained results above:

Then

So,the interpretation associated the sign of second order.

2.2 Strength Number

Without a doubt,the reproductive number has been utilized as a powerful mathematical tool to the stability of a mathematical model for a given infectious disease.While it has been used with some success,it has also been criticized as an insufficient tool to predict the behavior of the spread.For example,it was pointed out that there are several ways to obtain this value on the other hand.However,it was also argued that this value could not help humans t determine whether the model will determine waves.The concept of strength number has been suggested to further the analysis and will be used in this section.

The componentFAis obtained with deriving the nonlinear part of the infected classes.In our model there are two infected classes named byI1andI2.These infected classes given by

But we only use nonlinear part of infected classes.So we useclasses.Nonlinear part ofclasses is given by

In this case,we can have the following:

leads to

A0means there is no strength.Also there are more conlusion when strengh is zero

1)The disease will spread with a constant speed.

2)The disease will not renewal process therefore no new wave will be expected.

3)The magnitude of the spread will be the same at all time until extinction.

3 Applications of Piecewise Derivative

3.1 A Mathematical Model of Tuberculosis Epidemic Model with Piecewise Modeling

In this section,we present some applications of piecewise derivative for tuberculosis epidemic model such as

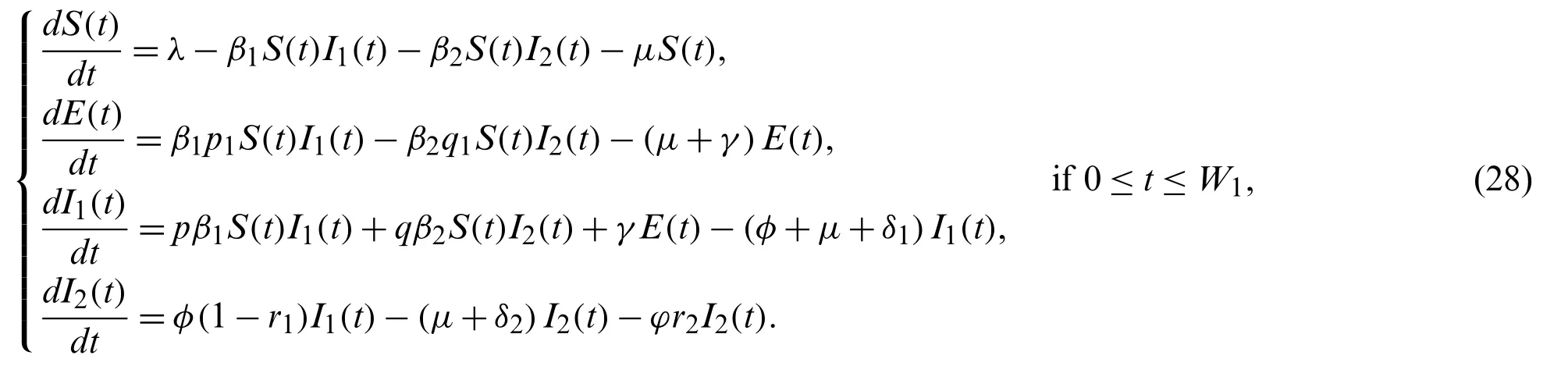
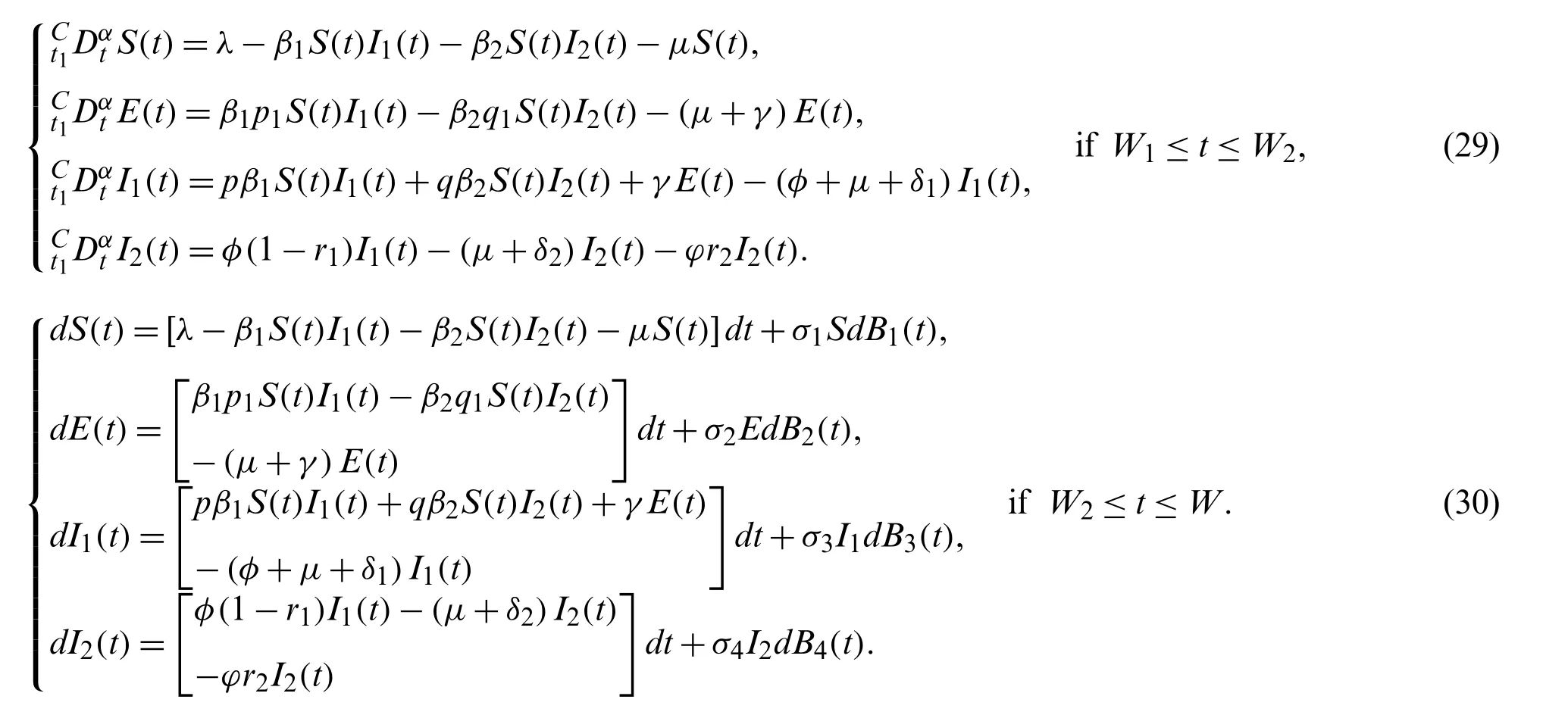
Let us give necessary conditions for the existence and uniqueness,we must prove that ∀[0,W1]and[W1,W2]fi(S,E,I1,I2)fori=1,2,3,4 satisfy

1)Linear growth condition

and

2)The Lipschitz condition

Let us write system as below:

For proof,we consider the function

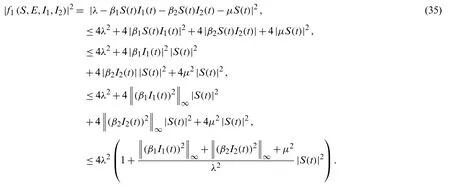
under the condition that

then we have

Using same routine

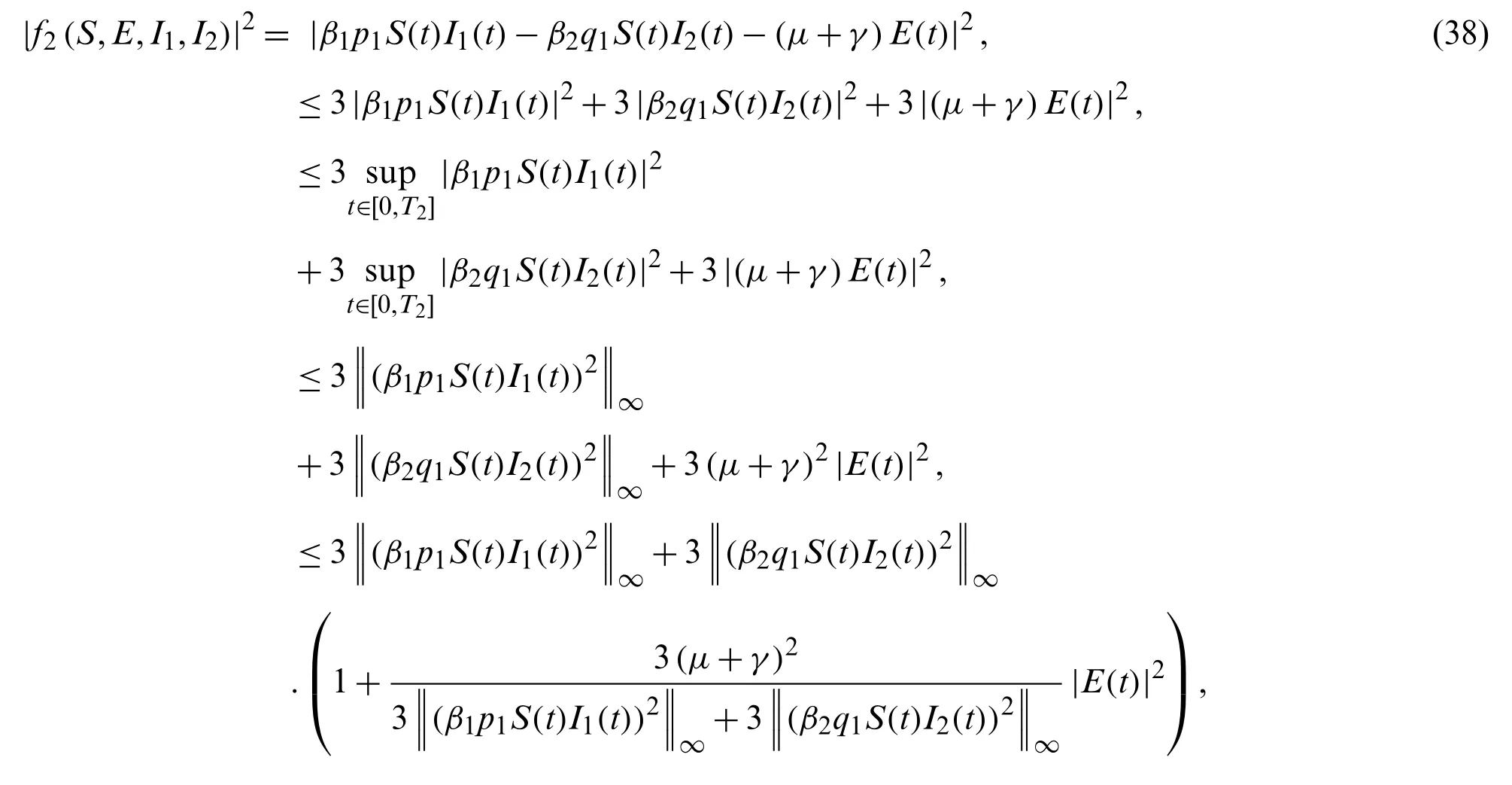
under the condition

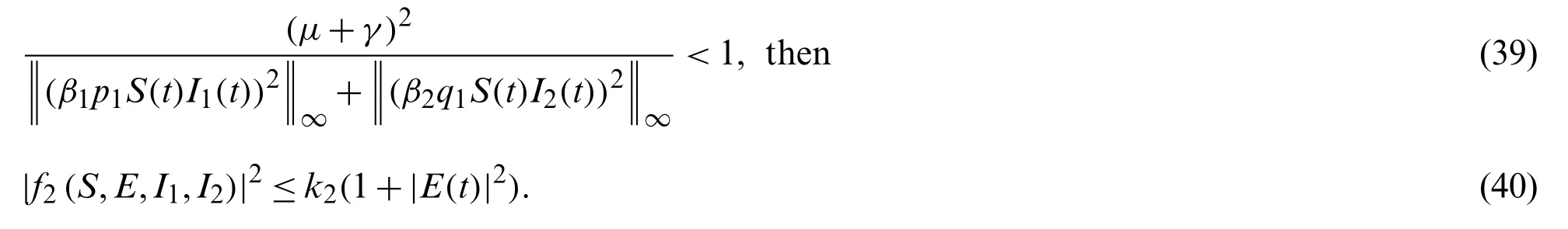
For the functionf3(S,E,I1,I2)

under the condition

Finally for the functionf4(S,E,I1,I2)

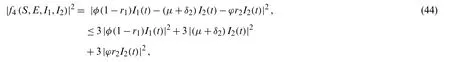
under the condition

Therefore the condition of linear growth is verified if

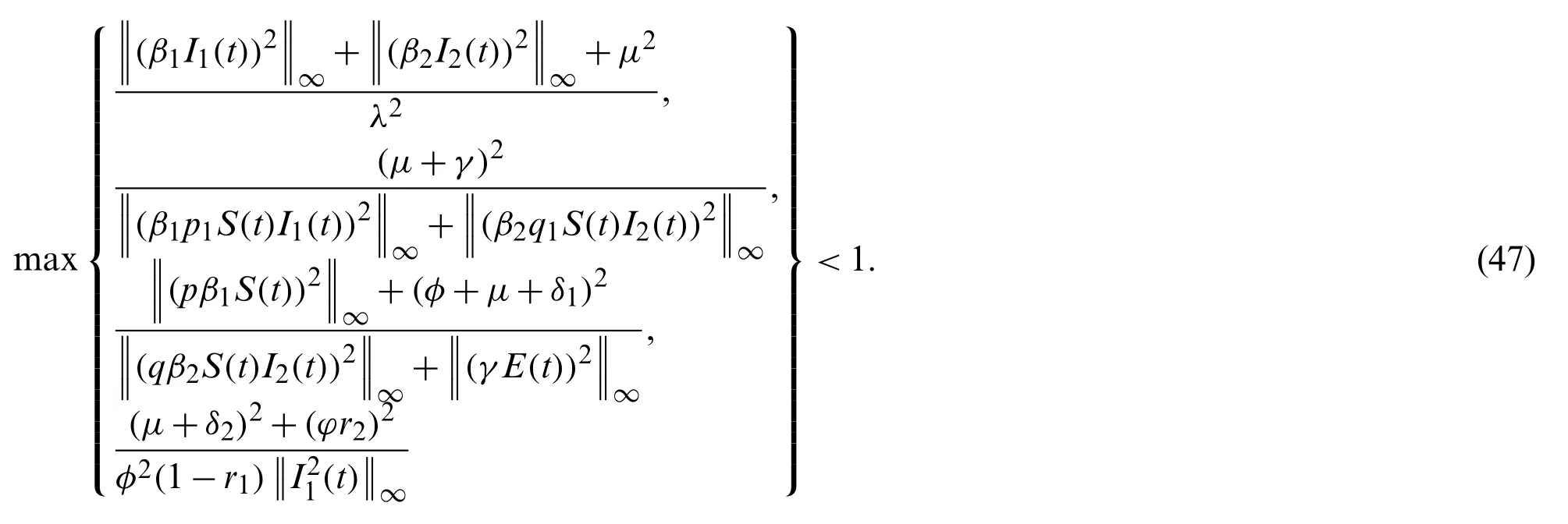
Now we have to verify Lipschitz condition for equations.

For the functionf1(S,E,I1,I2),

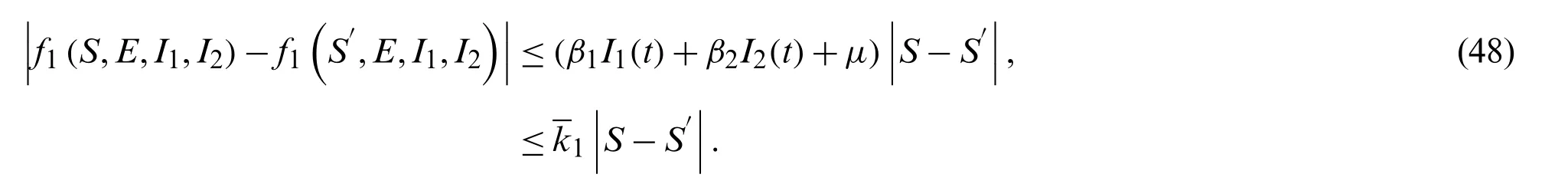
For the functionf2(S,E,I1,I2),

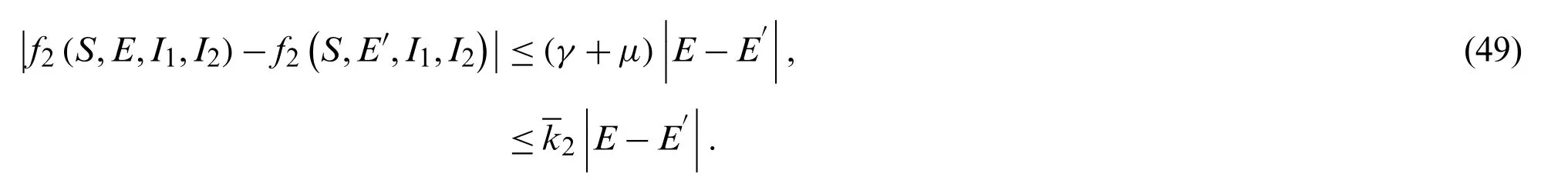
For the functionf3(S,E,I1,I2),

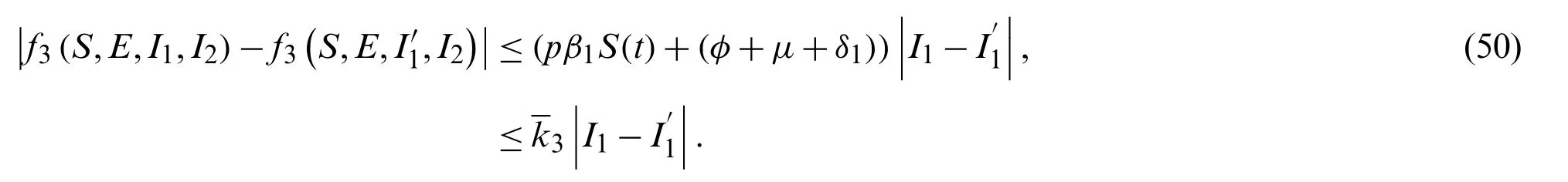
Finally for the functionf4(S,E,I1,I2),

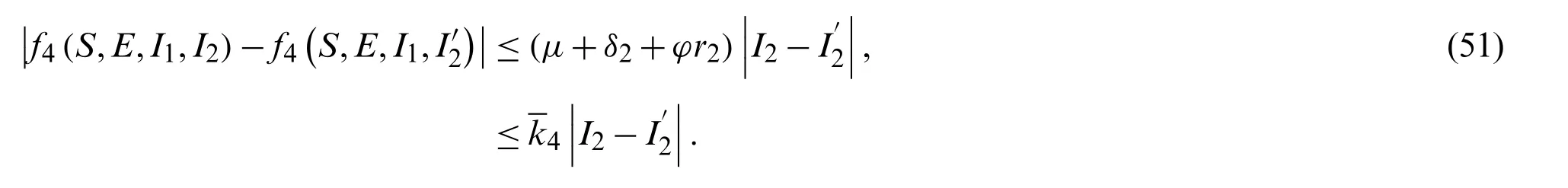
We verified the Lipschitz condition which completes the proof.

Let us do proof for last part of piecewise equation.Here we consider for ∀t∈[W2,W].In the model we take forS(t),E(t),I1(t)I2(t)∈[W2,τe),whereτeshows explosion time.To prove the solution is global,one has to prove that such system solution is global,so we have to prove thatτe=∞.

Now we considerl0∈R+is a positive constant such thatS(W2),E(W2),I1(W2)I2(W2)lies within.We define a stopping time as

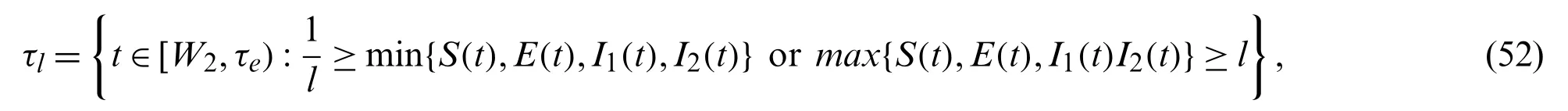
for eachl≥l0.While asl→∞,τlis monotonically increasing.∀t≥0,if we show thatτ∞=0,then we can conclude thatτe=∞andS(t),E(t),I1(t),I2(t)∈R4+is solution.So we have to prove thatτe=∞.

If we have contradictory for the conclusion,then there exists 0＜Wandε∈(0,1)such that

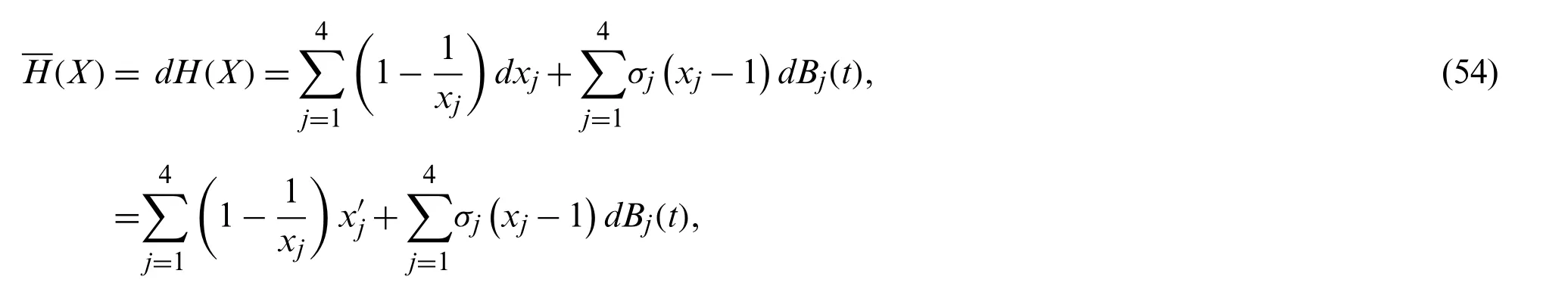
where

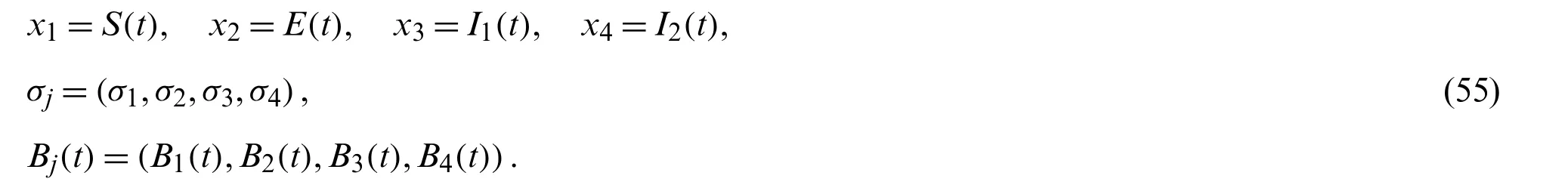
and

By taking integration from 0 toτl∧W,we have

SettingΠl={W ＞τl}forl1≤land thusP(Πl)≥ζ.

It is a contradiction.So under the conditions gived earlierτ∞=∞which completes the proof.

4 Numerical Schemes for Model with Four Waves Patterns

In this section,we generate a numerical schemes for spread of infectious(specially for pandemic)disease with four patterns.These schemes will consist of three derivatives with randomness[1,12].

4.1 Case 1:Classical-Power Law-Exponential Decay Law-Randomness

In this case,we consider a version with four waves which have classical derivative starts from 0 toW1,the power law derivative start fromW1toW2,the exponential decay law derivative start fromW2toW3,and the last fromW3toW.So a piecewise mathematical system that is defined as subsection can be given as

whereσiare densities of randomness andBiare the functions of noise.

4.2 Case 2:Classical-Power Law-Mittag-Leffler Law-Randomness

In this case,we consider a version with four waves which have classical derivative starts from 0 toW1,the power law derivative start fromW1toW2,the Mittag-Leffler law derivative start fromW2toW3,and the last fromW3toW.So a piecewise mathematical system that is defined as subsection can be given as

whereσiare densities of randomness andBiare the functions of noise.

4.3 Case 3:Classical-Power Law-Fractal-Fractional Power Law Derivative-Randomness

In this case,we consider a version with four waves which have classical derivative starts from 0 toW1,the power law derivative start fromW1toW2,fractal-fractional power law derivative start fromW2toW3,and the last fromW3toW.So a piecewise mathematical system that is defined as subsection can be given as

whereσiare densities of randomness andBiare the functions of noise.

4.4 Case 4:Classical-Exponential Decay Law-Fractal-Fractional Exponential Decay Law Derivative-Randomness

In this case,we consider a version with four waves which have classical derivative starts from 0 toW1,the exponential decay law derivative start fromW1toW2,fractal-fractional exponential decay law derivative start fromW2toW3,and the last fromW3toW.So a piecewise mathematical system that is defined as subsection can be given as

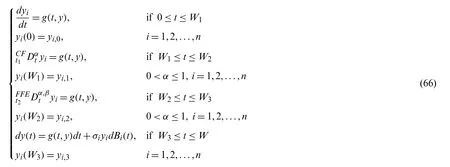
whereσiare densities of randomness andBiare the functions of noise.

4.5 Case 5:Classical-Mittag-Leffler Law-Fractal-Fractional Mittag-Leffler Law Derivative-Randomness

In this case,we consider a version with four waves which have classical derivative starts from 0 toW1,the Mittag Leffler law derivative start fromW1toW2,fractal-fractional Mittag-Leffler law derivative start fromW2toW3,and the last fromW3toW.So a piecewise mathematical system that is defined as subsection can be given as

whereσiare densities of randomness andBiare the functions of noise.

5 Numerical Schemes of Piecewise Epidemic Disease Models with Four Waves Patterns

In this section we assumed that those kind of epidemic models satisfy existence and uniqueness.So we can put numerical solutions for them.While putting solution results we use in all cases on the Lagrange polynomial interpolation.First we divide[0,W]in four

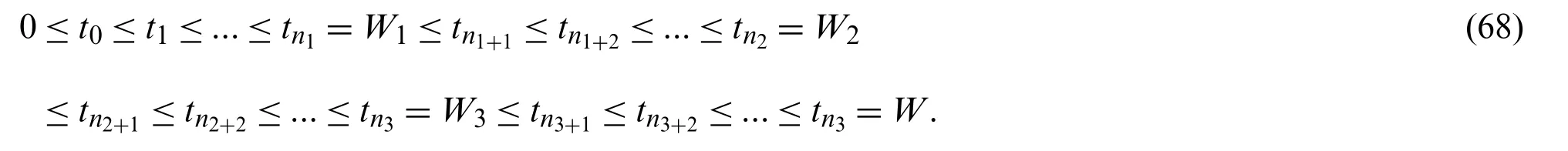
5.1 Numerical Method for Case 1:

Let us consider the first case

The numerical solution can then be provided as

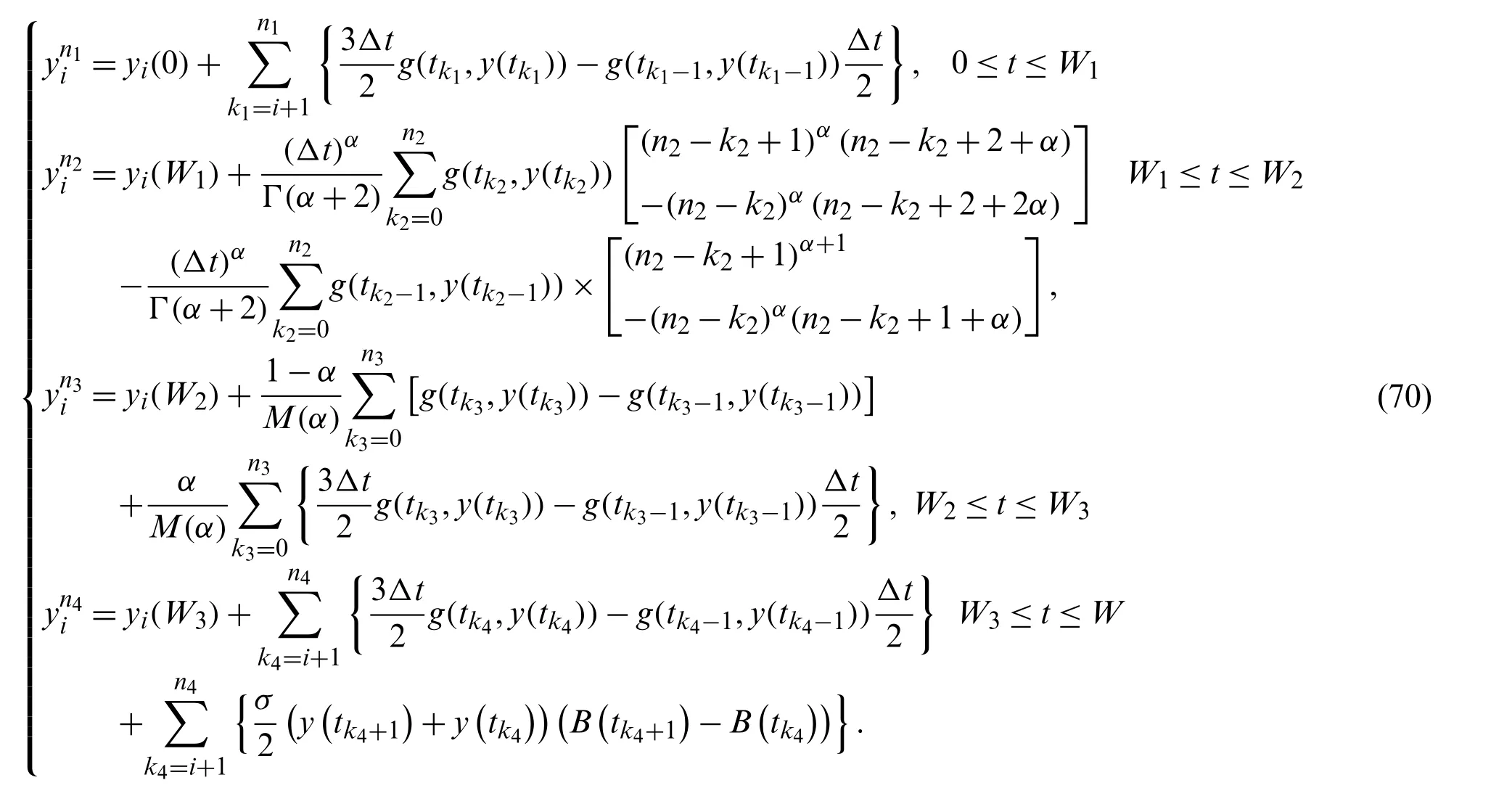
5.2 Numerical Method for Case 2:

We deal with the following problem with second case

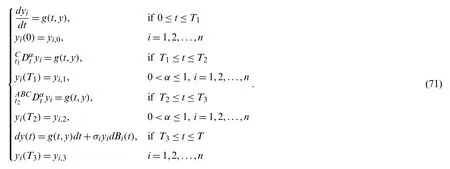
The numerical solution for such problem is given by

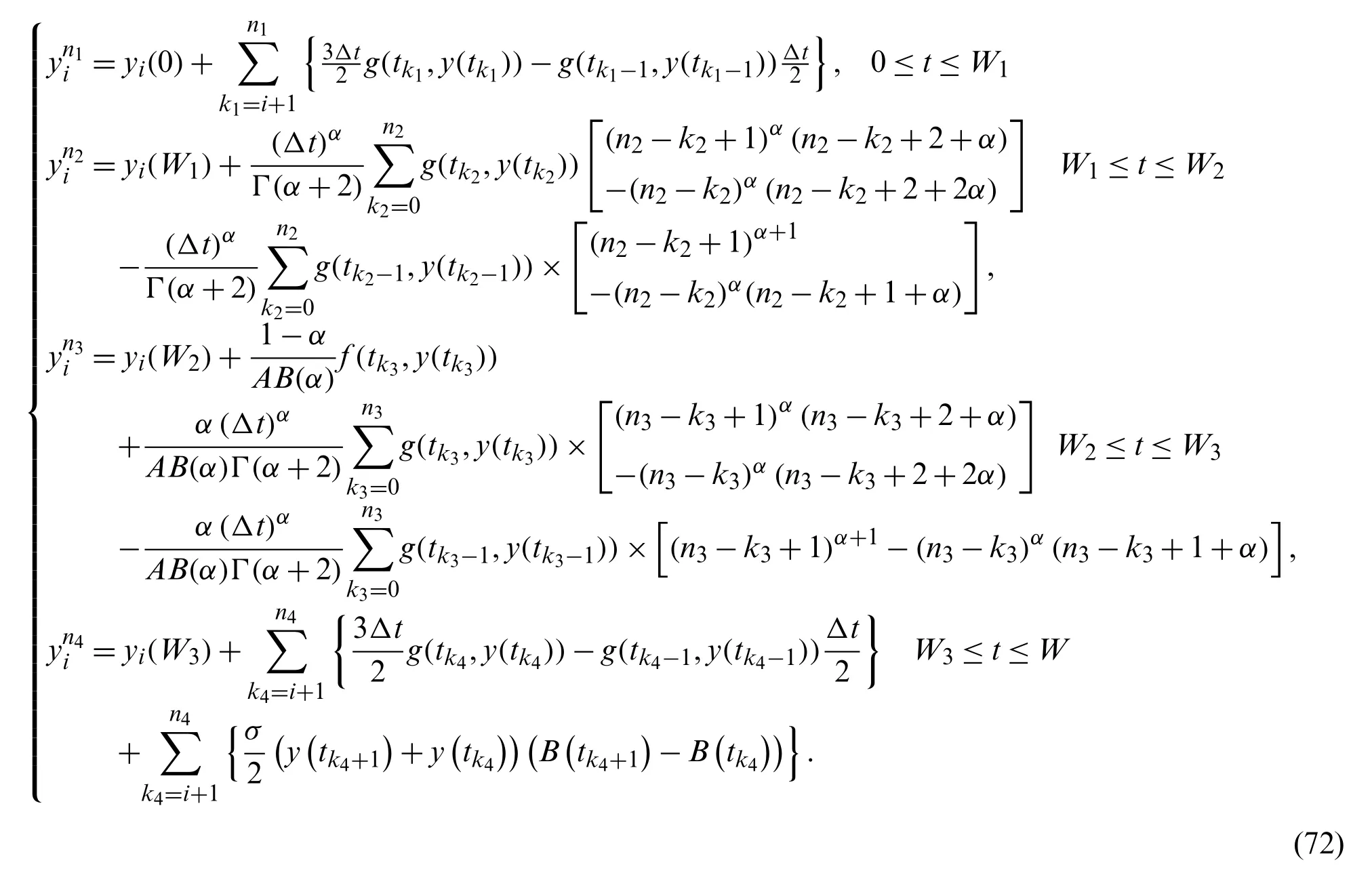
5.3 Numerical Method for Case 3:

Now we deal with the following problem with third case

The numerical solution for such problem is given by

5.4 Numerical Method for Case 4:

Here,we deal with the following problem with fourth case

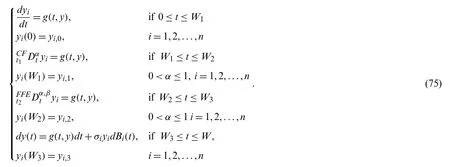
The numerical solution for such problem is given by

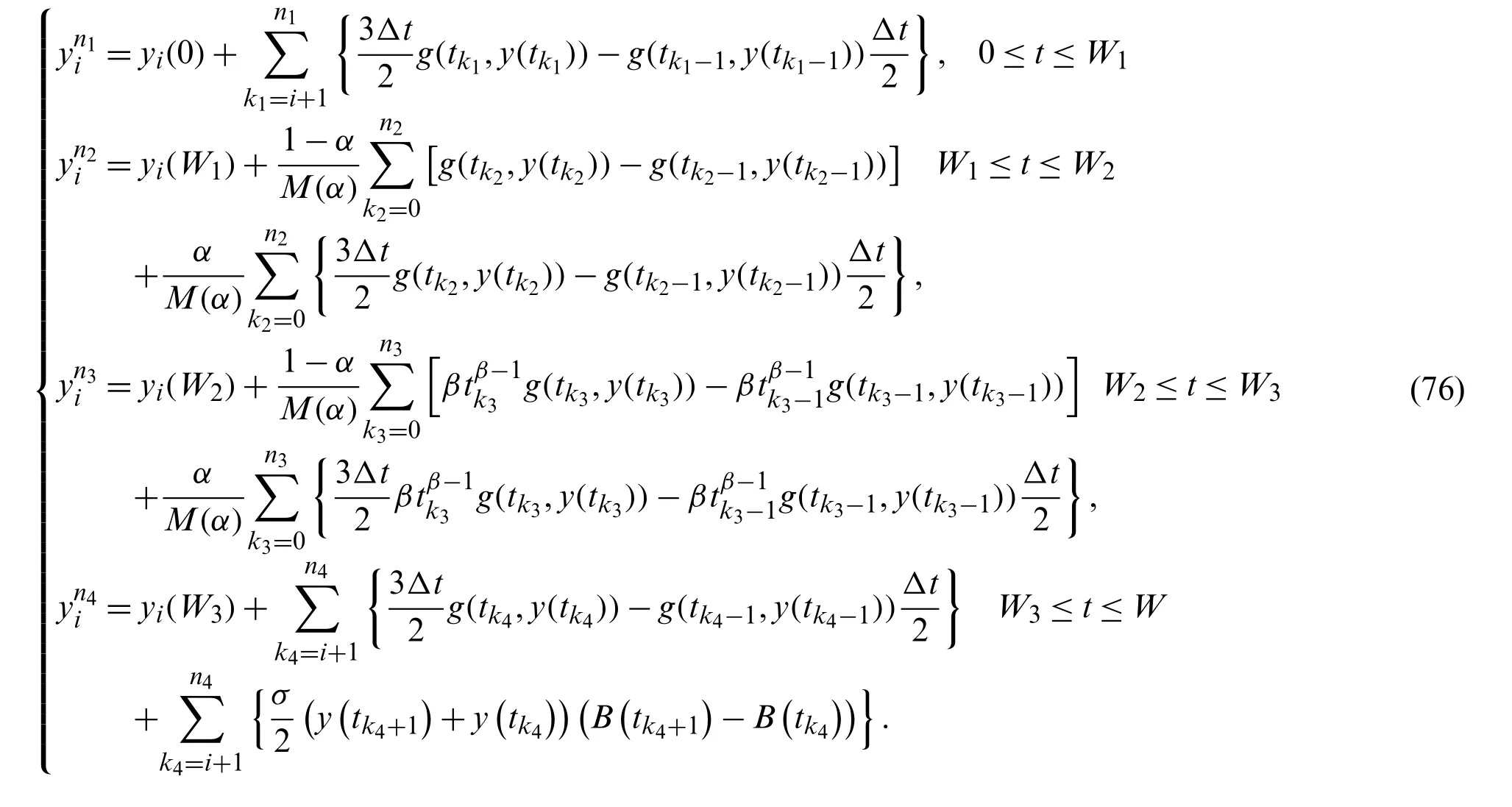
6 Numerical Method for Case 5:

Finally,we give numerical method with the following problem with fifth case:

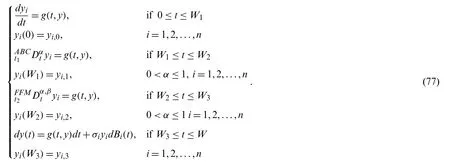
The numerical solution for such problem is given by

6.1 Numerical Simulation for Stochastic-Deterministic Model of Tuberculosis

In this section,we give numerical simulation of the Tuberculosis epidemic system of fractional stochastic differential equations.We have made use of the model with the piecewise differential operators and the numerical scheme where the Lagrange polynomial interpolation is used.While modelling with piecewise idea,the first part is classical,the second part is fractional and last part is stochastic.The numerical simulation is performed for different values of fractional orders.So the stochastic-deterministic piecewise tuberculosis model is given as

For simplicity we consider right side of system as

Using the numerical scheme presented in this paper with piecewise derivative,the numerical solution of the stochastic-deterministic tuberculosis model is given as follows:

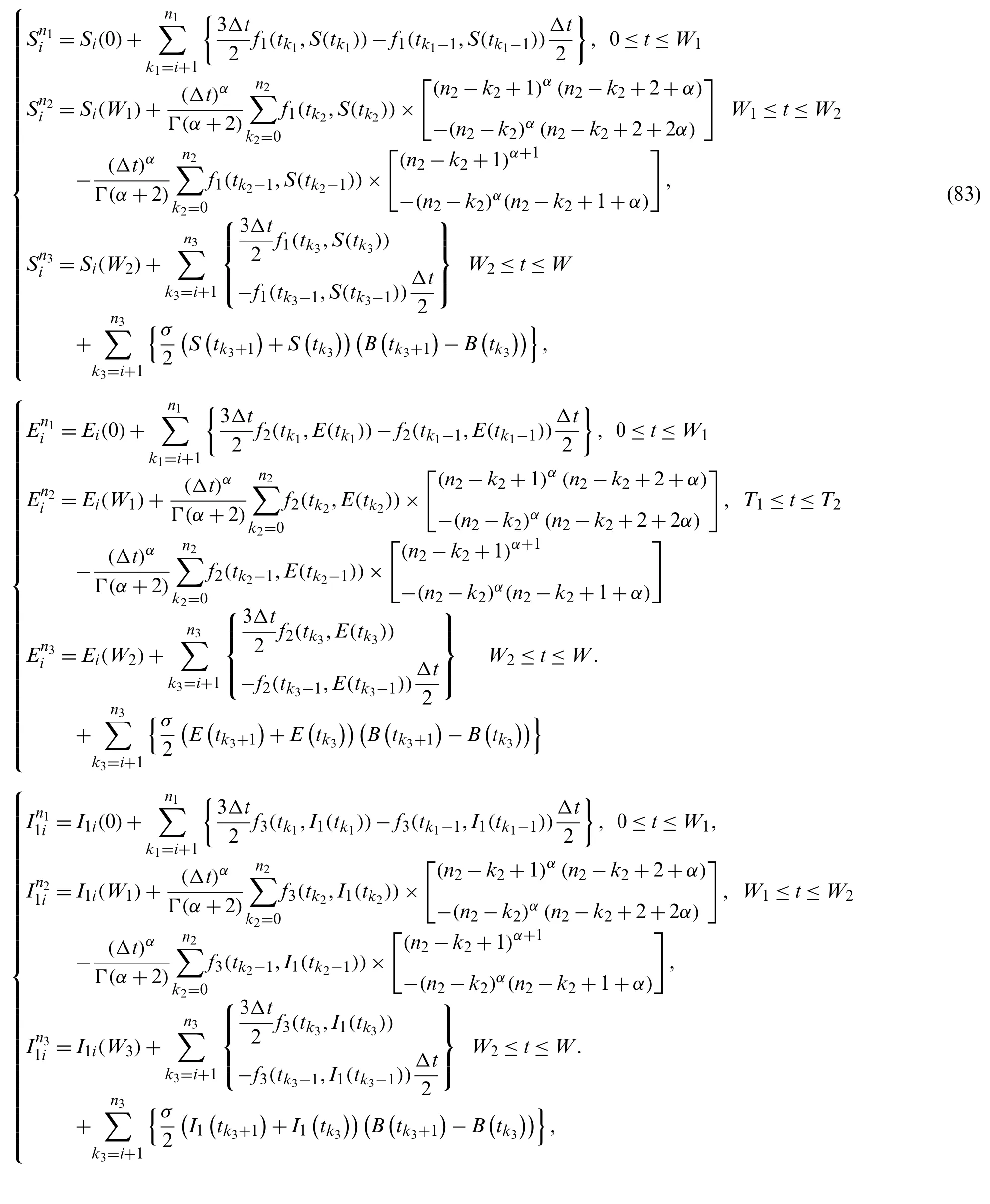
7 Numerical Simulations

In this section,we will deal with numerical simulation of the Tuberculosis epidemic system of fractional stochastic differential equations.in order to demonstrate that the proposed method is effective and accurate.We have made use of the model with the piecewise differential operators and the numerical scheme where the Lagrange polynomial interpolation is used.In the numerical scheme,the first part is classical,the second part is fractional and last part is stochastic.We also present the results obtained from the fractional stochastic model,the numerical simulations are shown in Fig.1 for alpha=1,Fig.2 for alpha=0.5,Fig.3 for alpha=0.6 and finally Fig.4 for alpha=0.9 with density of randomness given by sigma1=0.01,sigma2=0.015,sigma3=0.012,sigma4=0.010.And with same alpha values but different density of randomness given by sigma1=0.1,sigma2=0.2,sigma3=0.3,sigma4=0.4 we put Figs.5–8.Also figures including the initial conditions as

S(1)=180,E(1)=130,I1(1)=160,I2(1)=140.

Figure 1:Numerical simulation for alpha=1

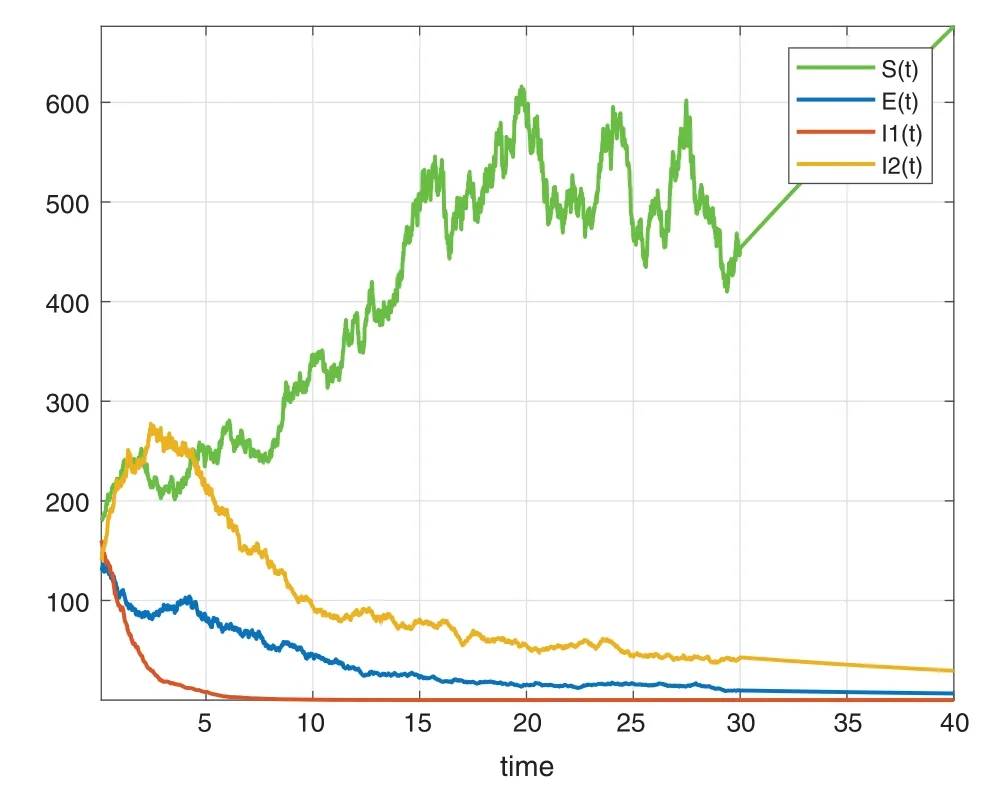
Figure 2:Numerical simulation for alpha=0.5

Figure 3:Numerical simulation for alpha=0.6

Figure 4:Numerical simulation for alpha=0.9

Figure 5:Numerical simulation for alpha=1

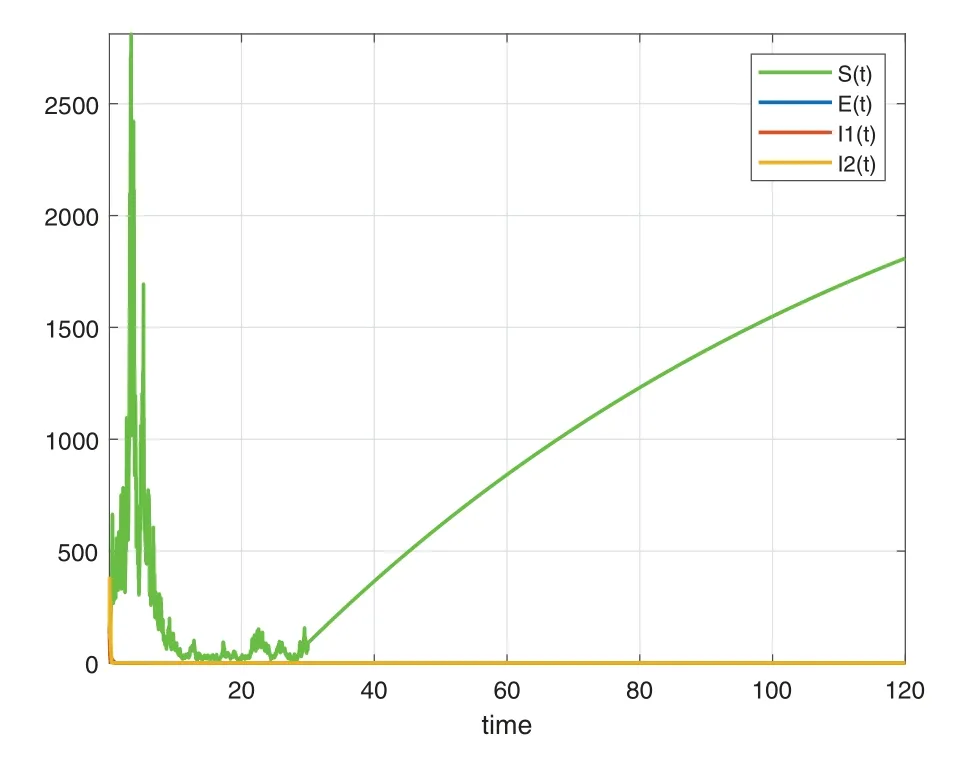
Figure 6:Numerical simulation for alpha=0.5

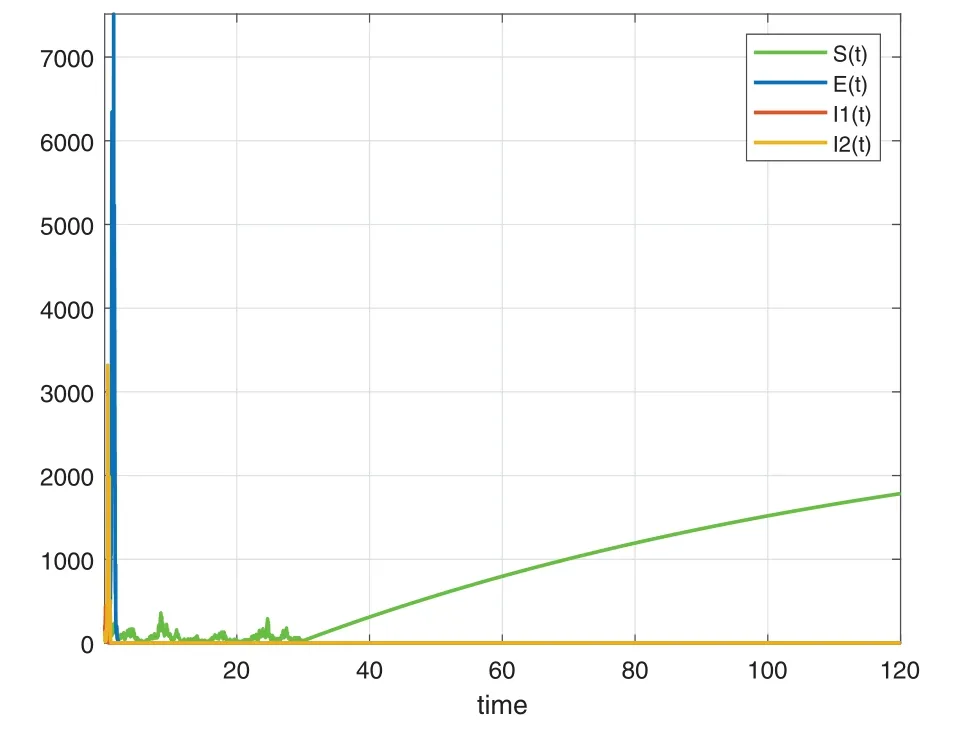
Figure 7:Numerical simulation for alpha=0.6

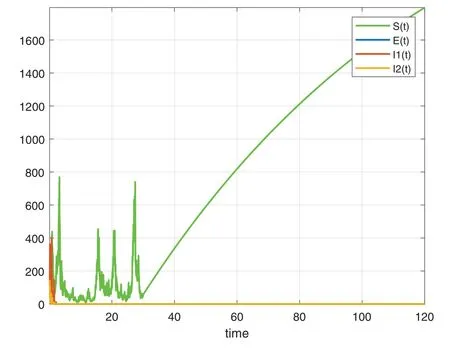
Figure 8:Numerical simulation for alpha=0.9

8 Conclusion

The spread of tuberculosis within human settlements and has infected and killed millions of humans in the last 200 years.While researchers from all backgrounds have put their efforts together to combat this virus and try to stop its spread,several studies have been performed;however,the virus is still spreading so far.Mathematical models are used to predict the future development of a given real-world problem.While several techniques and models have been proposed,they have not predicted piecewise behaviors of the spread.In this work,we attempted to present a model with piecewise patterns.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.