Efficient Numerical Scheme for the Solution of HIV Infection CD4+T-Cells Using Haar Wavelet Technique

Rohul Amin,S¸uayip Ÿuzbas¸ıand Shah Nazir

1Department of Mathematics,University of Peshawar,Peshawar,25120,Pakistan

2Department of Mathematics,Faculty of Science,Akdeniz University,Antalya,Tr-07058,Turkey

3Department of Computer Science,University of Swabi,Swabi,23430,Pakistan

ABSTRACT In this paper,Haar collocation algorithm is developed for the solution of first-order of HIV infection CD4+T-Cells model.In this technique,the derivative in the nonlinear model is approximated by utilizing Haar functions.The value of the unknown function is obtained by the process of integration.Error estimation is also discussed,which aims to reduce the error of numerical solutions.The numerical results show that the method is simply applicable.The results are compared with Runge-Kutta technique,Bessel collocation technique,LADM-Pade and Galerkin technique available in the literature.The results show that the Haar technique is easy,precise and effective.

KEYWORDS System of nonlinear differential equations;HIV infection of CD4+ T-cells;Broyden method;Haar wavelet;residual error estimation

1 Introduction

Many models have been developed by mathematicians in the last decade to explain the immunological response to Human Immunodeficiency Virus(HIV)infection.Due to the scarcity of CD4+T-cells,HIV disease is considered to result in concealment of the immune system(referred to generally as T4-cells or T-helper cells),cells which play a focal part in the human immune system.A class of white blood cells called CD4+T-cells is essentially infected by HIV and this selective depletion of CD4+T-cells means that a focal part in the resistant direction fills in as a clinical marker to estimate HIV disease movement.Mathematical models play an important role in the dynamics of these infectious diseases[1–6].The level of CD4+T-cells in the fringe blood is controlled at a level between 800 and 1200 mm-3in a normal human body.These cells are the most inexhaustible white blood cell of the human safe framework,which battle against diseases[7].Many authors introduced different numerical methods for the investigation of CD4+T-cells[8–14].

In recent years,many researchers have studied on new analytical and numerical methods for model problems characterized by differential equations.Yüzba¸si et al.[15]presented the Pell–lucas collocation method for the solutions of two population models and residual correction.Mallawi et al.[16]utilized Legendre collocation method to the space–time variable fractional-order advection–dispersion equation.Yüzba¸si[17]used an operational method for solutions of Riccati type differential equations.Chu et al.[18]studied the generalized(2+1)dimensional shallow water equation.The solution for the fractional system of HIV-1 infection of CD4+T-cells was studied by Khater et al.[19]by using Atangana–Baleanu fractional derivative.Khater et al.[20]developed a semi analytical and numerical scheme for a biological model.Khater et al.[21]used the trigonometric quintic B-spline technique for the solutions of complex nonlinear Fokas–Lenells equations.In reference[22]the nonlinear phi-four equation is solved through two analytical and semi-analytical techniques.Khater et al.[23]used trigonometric Quintic B-spline method for the solution of conformable fractional nonlinear time-space telegraph equation.Khater et al.[24]investigated the analytical and numerical solutions of the modified Benjamin–Bona–Mahony equation via the modified B–spline collection method.Khater et al.[25]found the solution of nonlinear Klein–Fock–Gordon equation by using generalized exponential function and generalized Riccati expansion methods.Khater et al.[26]investigated the analytical and semi-analytical solutions of the time-fractional Cahn–Allen equation by using the Adomian decomposition method.Khater et al.[27]found the analytical solutions of the nonlinear Schrodinger equation with the higher-order through Kudryashov method.They also found the solutions of quadratic cubic fractional nonlinear Schrodinger equation by Adomian decomposition process[28].Khater et al.[29]used the trigonometric quintic and exponential cubic B-spline schemes for the solutions of the nonlinear Klein-Gordon-Zakharov model.Yue et al.[30]found a solution of the fractional nonlinear Hirota–Satsuma–Shallow water wave equation by using a modified Kudryashov method.Khater et al.[31]found solutions of the Fisher-Kolmogorov-Petrovskii-Piskunov model by employing the modified Kudryashov and trigonometric-quantic B-spline methods.Li et al.[32]found wave solutions of the(2+1)dimensional Kadomtsev Petviashvili Benjamin Bona Mahony model.Smadi et al.[33]study the accuracy of solution for fractional order an SEIR epidemic model by using the homotopy analysis method.Freihet et al.[34]found a solution of a fractional stiff system using residual functions algorithm.Smadi et al.[35]developed analytical technique for coupled system of fractional partial differential equations,for solutions of nonlinear fractional Kundu-Eckhaus equations[36]and for solution of coupled fractional resonant Schrodinger equations[37].The same authors analyzed and investigated the analytical solution of the seventhorder fractional Sawada Kotera Ito,Lax,and Kaup Kupershmidt equations[38].Moreover,the authors also analyzed and studied fuzzy fractional differential equations in terms of Atangana-Baleanu Caputo differential operators equipped with uncertain constraints coefficients and initial conditions[39].

Here we develop an accurate scheme by using HWC technique for the solution of the HIV infection of CD4+T-cells.The main contributions of this work as:

·To develop efficient numerical scheme by utilizing HWC technique for HIV infection CD4+T-cells

·To design numerical scheme using HWC technique

·To evaluate the efficacy of the established technique in some instances and compare the results with other techniques Runge-Kutta,LADM-Pade[1],Bessel collocation technique[2],PIA(1,1)[3],MVIM[4],DTM[7]and Galerkin technique[5]available in the literature

In this article we find the numerical solution of first order model of the form[5]

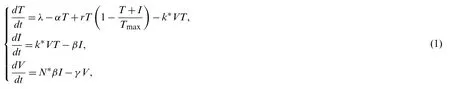
with initial conditions:

HereT(t),I(t),V(t)are used for concentration of uninfected cells,infected cells and free virus particles of CD4+T-cells by HIV in the blood.is logistic growth of the healthy cells,Tmaxis the most extreme level of cells in the human body,kis the steady rate which the body produces cells,k*VTis the frequency of HIV infection of healthy cells,k*＞0 is the rate of virus infection,N*βis the rate of virus production by contaminated cells,whereN*is the average number of particles of infection produced by the infected T-cell,andγis the rate of death of particles of the virus.

The paper is structured as:In Section 2,Haar functions are defined.HWC technique for solution of HIV infection is given in Section 3.In Section 4 error estimation about the model is given.In Section 5,one example is given.Conclusion is given in the last Section 6.

2 Haar Wavelet

Here we discuss Haar functions,integration of Haar functions and collocation points.

Definition 2.1.Scaling function on[α1,α2)is[40]

Mother wavelet on[α1,α2)is

The other terms can be written as

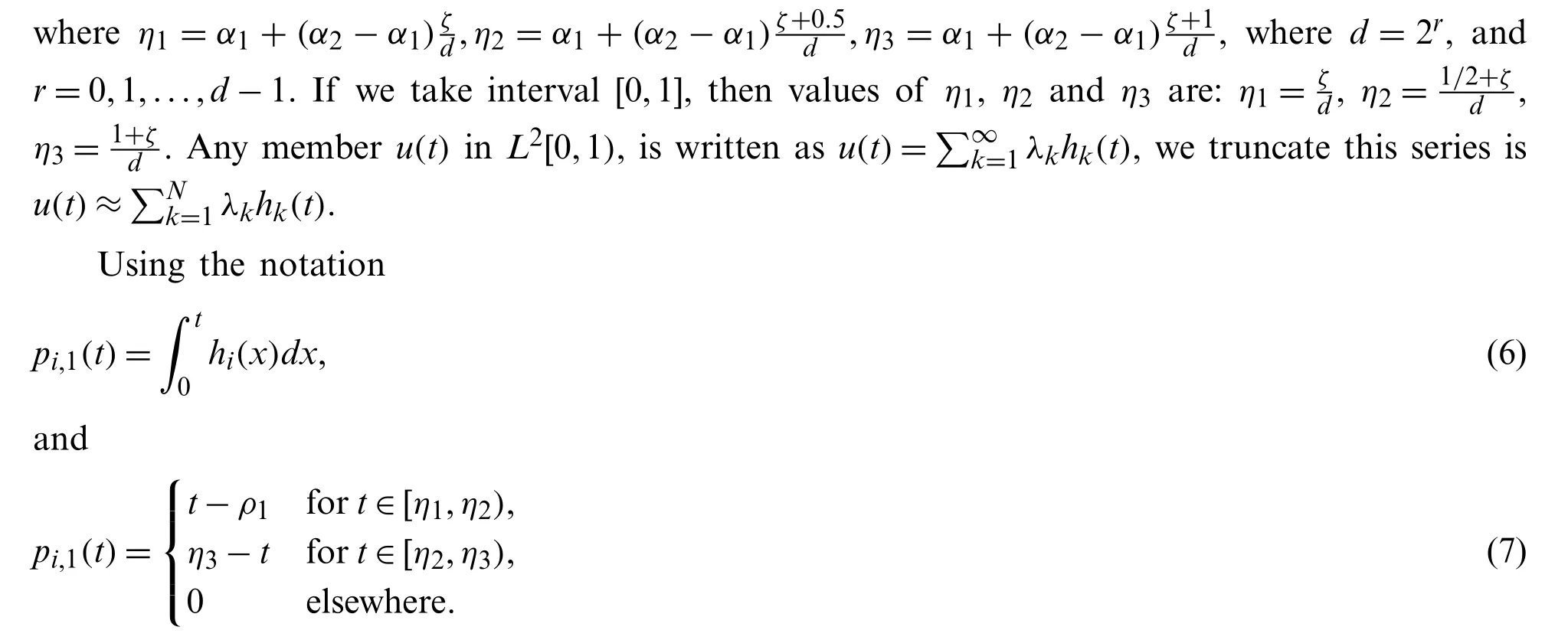
3 Numerical Method

The implementation of the HWC method is discussed in this section in order to find the HIV model solution provided in Eq.(1).Using Haar functions,the derivative of the unknown function in the method is approximated and the expression for the unknown function is obtained by using initial condition and integration.By applying the Haar technique to Eq.(1)and putting the CPs,we get a system of algebraic equations.The Broyden technique is used to find solution of this system.At last,the approximate solution at CPs is obtained using these coefficients.We use the symbols.

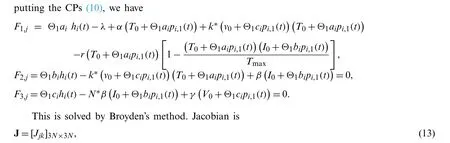
where

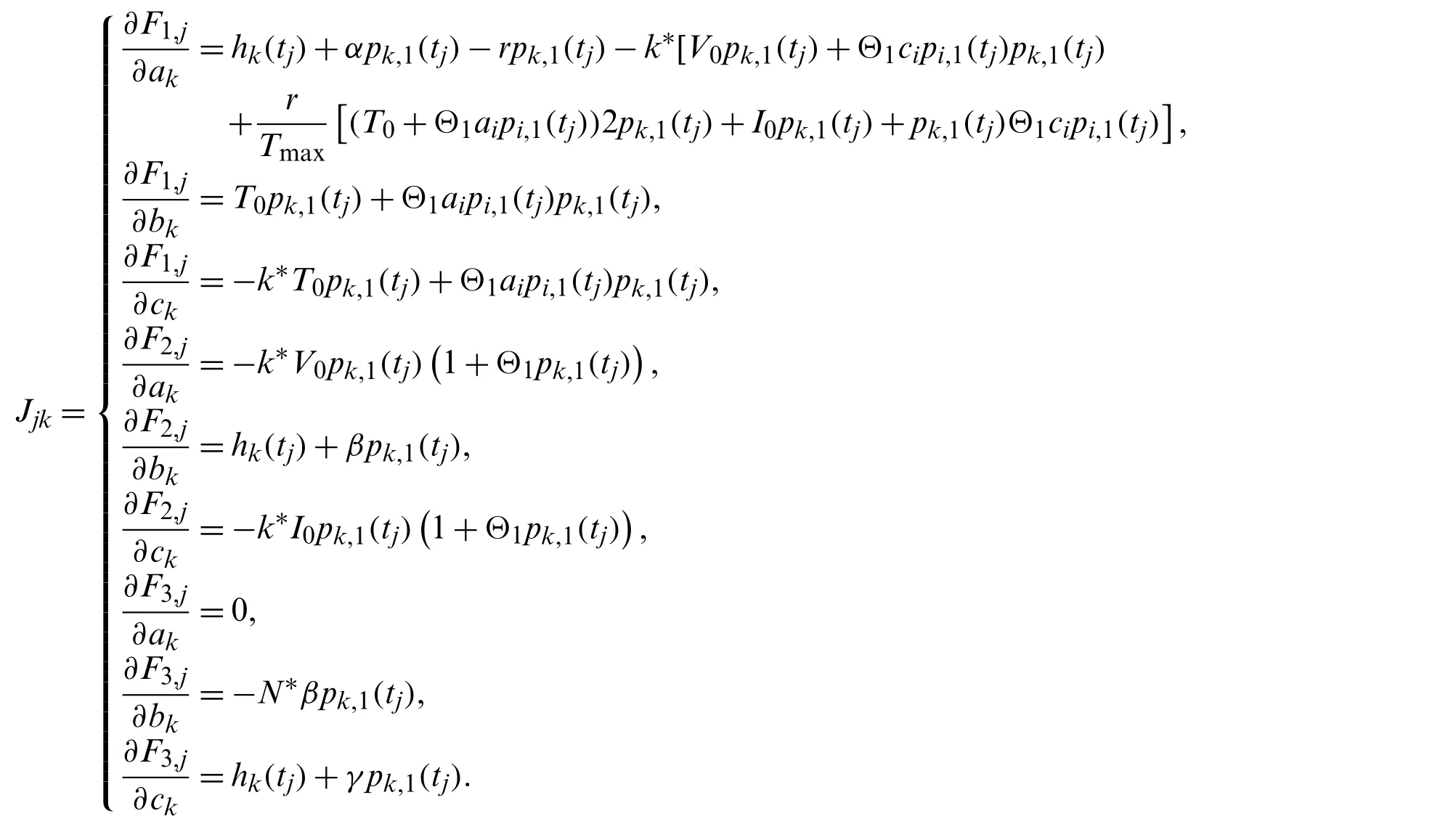
The solution of this gives the values of unknown coefficientsai’s,bi’s andci’s.The required solutionTN(t),IN(t)andVN(t)at CPs is calculated by puttingai,bi ci’s in Eq.(12).

4 Error Estimation

Here,we study the residual error estimation[5]for HIV model(1)utilizing HWC technique.The residual functionsR1,N(t),R2,N(t)andR3,N(t)are

The unknown coefficientsξi,μiandνiare obtained from the solution of this system.The approximate solution at discrete CPs is obtained by pluggingξi,νi νi i=1,2,...Min Eq.(22).Substituting the values ofe1,N,M(t),e2,N,M(t)ande3,N,M(t)in system(16),we get the required solution.

5 Numerical Applications

The performance of the HWC technique is tested on example in this section.The numerical results are compared with Runge-Kutta technique,Bessel collocation technique,LADM-Pade and Galerkin technique available in the literature.

Problem 1.Consider the following system[5]

By using initial conditions and integration,we obtain the approximate solution of this system in terms of Haar functions

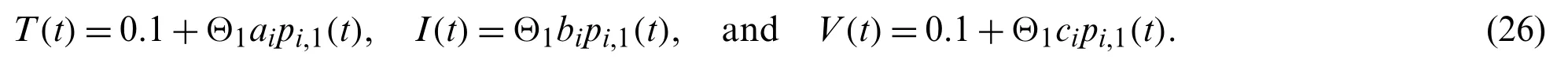
Putting these approximations and CPs in above system(24),we obtain a system of nonlinear algebraic equations which is then solved by the method of Broyden’s.Error estimation is also calculated in a similar way,which aims to reduce the error of numerical solution.The residual functionsR1,N(t),R2,N(t)andR3,N(t)are calculated as discussed in Eq.(14).The errors functionse1,N(t),e2,N(t),ande3,N(t)are obtained as discussed in Eq.(15).

The error functions for distinct CPs and distinct values of time are given in Tables 1–3.The error functions obtained for variableN=3 at different values oftare compared with Laplace Adomian decomposition technique,Runge-Kutta technique,modified variational iteration technique,Pade approximation,the perturbation-iteration algorithm,Bessel collocation technique,differential transform technique and exponential Galerkin technique available in literature.From the tables we see that asNincreases,the values of our results near to those of the other techniques.This show that our approximate solution become accurate as the number of discrete CPsNincreases.Even a batter accuracy is obtained by taking more discrete CPs.The graph of numerical solution is also given in Fig.1.The estimated results of error functions for distinct number of CPs are shown in Fig.2.Due to the simplicity of the Haar wavelet it is effective for solution of the first-order of HIV infection CD4+T-Cells model.However,HWC scheme has disadvantages too.This method use constant box functions and due to this we need a large number of collocation points in order to achieve better accuracy.This disadvantage can be overcome if Haar wavelet is replaced with some other wavelets having better approximating properties.

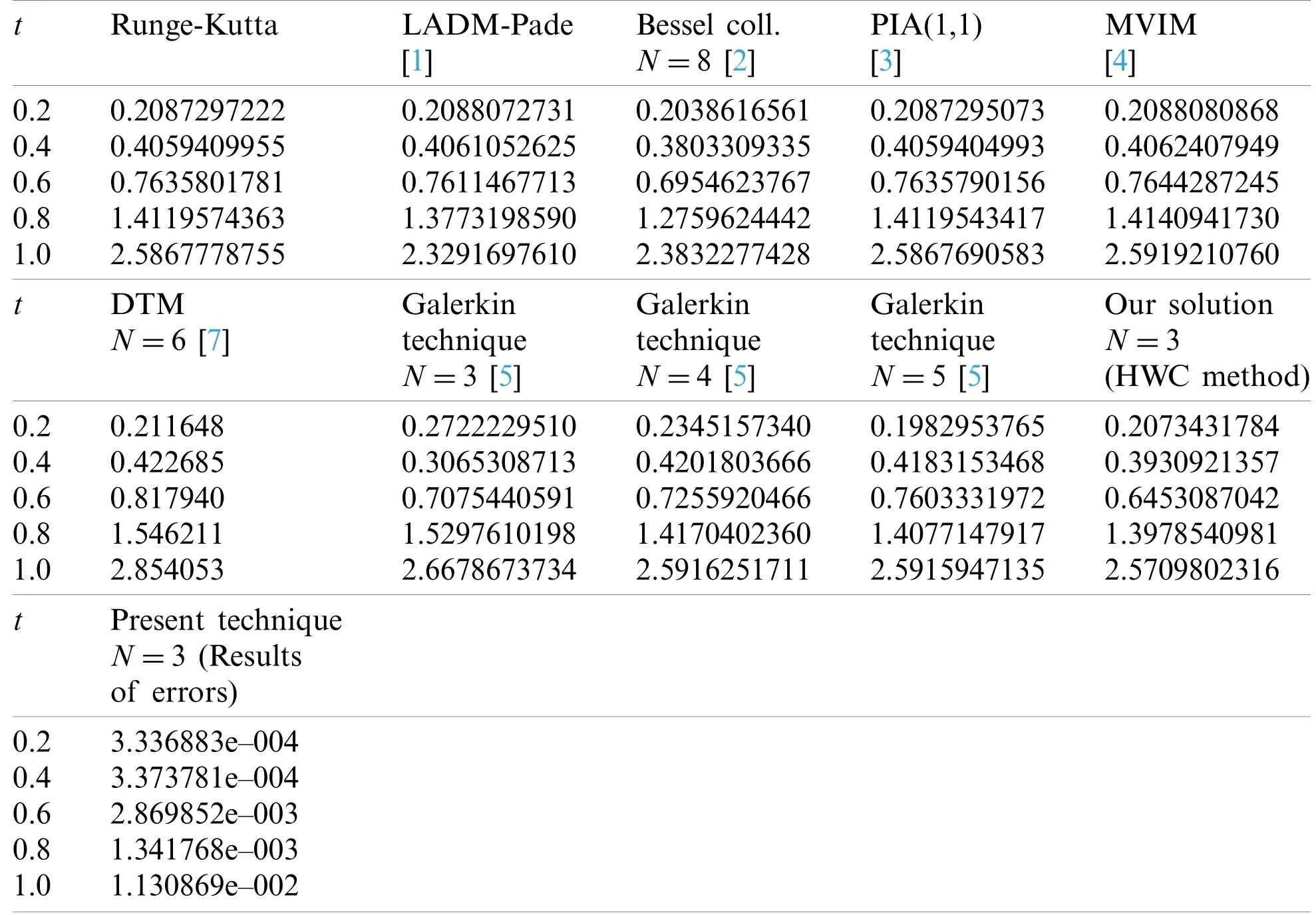
Table 1:Comparison for uninfected cells T(t)

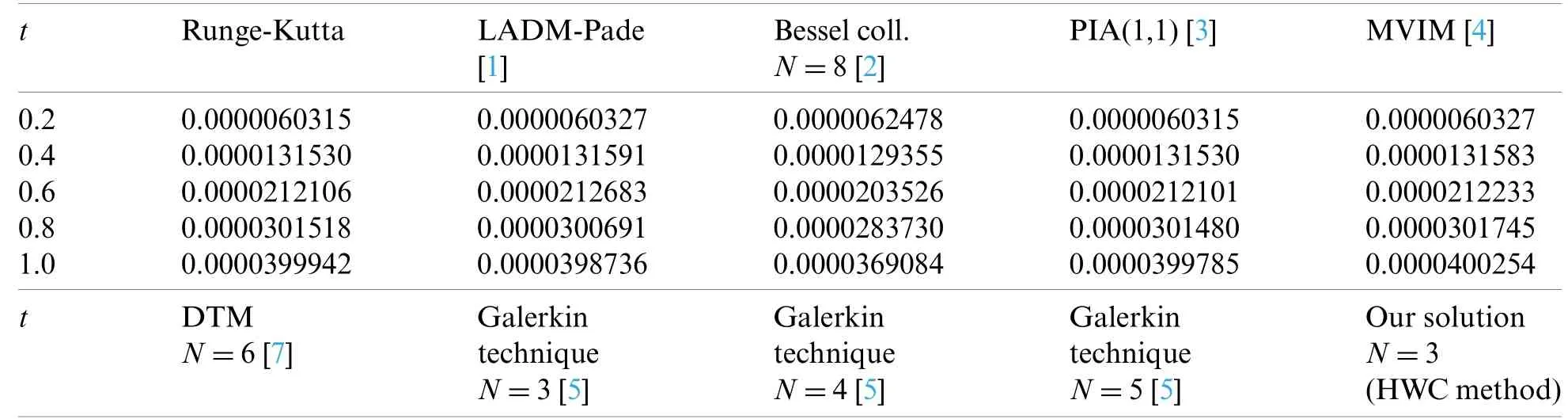
Table 2:Comparison for infected I(t)

Table 2(continued)0.20.00000636660.00000916730.00000582510.00000596410.0000070416 0.40.00001399240.00001552290.00001340510.00001313400.0000140251 0.60.00002265140.00002284590.00002134050.00002126820.0000230126 0.80.00003328360.00003184860.00003013130.00003017540.0000309231 1.00.00004853990.00004210570.00004003690.00004003770.0000403894 t Present technique N=3(Results of errors)0.21.688238e–008 0.41.754047e–008 0.61.732461e–006 0.81.865676e–006 1.01.961419e–006

Table 3:Comparison for free virus particles V(t)

Figure 1:Numerical solution of problem 1

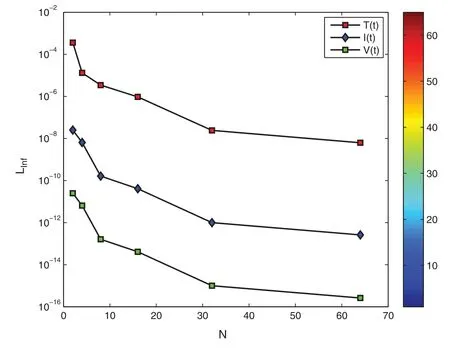
Figure 2:Estimated error functions for problem 1

6 Conclusion

Haar collocation scheme is developed for the solution of the HIV CD4+T-cells model.Also,we discussed a procedure known as residual error estimation,whose aim is to get better arrangements utilizing the obtained solution.The technique is tested on one example,and the results are compared with other methods available in the literature.The comparison of the present HWC technique with Runge-Kutta technique,Bessel collocation technique,LADM-Pade and Galerkin technique is given.The results demonstrate that Haar technique is effective and precise for distinct numbers of CPs.The results show that taking the large value of variableN,the HWC technique give the accurate results of the numerical solution.The error functions using various numbers of CPs are also calculated and reported in the table.From results,it is seen that proposed technique gives good results for this model.The proposed technique is easily implemented in any software packages.MATLAB software is used to obtain the numerical results.

Acknowledgement:The authors are very grateful to the anonymous referees for their constructive comments which have improved the paper.

Funding Statement:No funding is available to support this study.

Conflicts of Interest:On behalf of all authors,the corresponding author states that there is no conflict of interest.