Computational Investigation of Cell Migration Behavior in a Confluent Epithelial Monolayer

Jie Bai and Xiaowei Zeng

Department of Mechanical Engineering,University of Texas at San Antonio,San Antonio,78249,USA

ABSTRACT Cell migration plays a significant role in many biological activities,yet the physical mechanisms of cell migration are still not well understood.In this study,a continuum physics-based epithelial monolayer model including the intercellular interaction was employed to study the cell migration behavior in a confluent epithelial monolayer at constant cell density.The epithelial cell was modeled as isotropic elastic material.Through finite element simulation,the results revealed that the motile cell was subjected to higher stress than the other jammed cells during the migration process.Cell stiffness was implied to play a significant role in epithelial cell migration behavior.Higher stiffness results in smaller displacement and lower migration speed.

KEYWORDS Epithelial monolayer;cell migration;cell stiffness;intercellular interactions;finite element simulation

1 Introduction

Many biological activities such as embryogenesis[1–4],wound healing[5–7]and cancer metastasis[8–11]require collective cell migration in a coordinated way within a tissue[8,12–14].Cells in these tissues are often densely packed together,and the motion of a cell is often strongly constrained by its neighbors[15].When cellular movements are comparatively small,cellular rearrangements rarely happen,and cells are trapped by their immediate neighbors.Park et al.[16]performed a statistical analysis of these quasi-static collective cell motions which described such a cell layer to be solid-like and jammed.However,when cell movements are comparatively large in a cooperative way and swirling pattern,such a layer is described to be fluid-like and unjammed.The jammed to unjammed transition has been found in cancer metastasis,organogenesis,bronchial asthma,etc.[17].Initiation of some biological processes such as tissue remodeling and wound repair require the quiescent cell layer to transit from jammed state to unjammed state via collective migration.During the cell migration process,the individual cell of the unjammed collective cells interacts with its neighbors cooperatively through chemical and mechanical cues.The cell jamming/unjamming transition is superficially similar to the epithelial-to-mesenchymal transition(EMT)which has also been shown to occur in wound healing.Although their distinctions have been investigated[18],still little is known on unjammed-to-jammed transition for the densely packed cells.

Collective cell migration has received growing attention in recent studies which show that the cell migration behavior is governed by a set of parameters.Active motility,cell density,cellcell interaction,cell shape,cell stiffness and applied stress are believed to be potential factors that can affect the collective cell migration behavior[19].Experimental studies[16,20–22]have found that during collective cell migration,not only the leader cell may play an important role,but cell-cell adhesion forces may also influence the migratory behavior.By using the Monolayer Stress Microscopy,Park et al.[16]found that the jamming/unjamming transition in asthma is linked to cell shape change.As the layer becomes more unjammed,the cell shape changes from regular hexagonal to more elongated and more variable shape-like.It also showed the intercellular stresses are higher in unjammed bronchial epithelial cells from asthmatic donors compared with those in jammed cells from non-asthmatic donors.By studying the developing monolayers of human bronchial epithelial cells,Garcia et al.[23]found cell-cell contacts and cell-substrate contacts maturate with time,resulting in higher friction between cells that may influence the cell jamming/unjamming transition.Experiments have identified that intercellular adhesion force is regulated by proteins that resist and transmit forces at cell-cell junctions[12,24].Studies have also shown that cell stiffness may also influence cell motility during the migration process[25–27].

On the other hand,researchers have used numerical tools of various complexity to investigate the collective cell migration behavior.The cellular Potts model(CPM)[28,29]was one of the early successful models.In the CPM[30,31],cells are considered as several sets of pixels that are updated by certain probabilistic rules.Different particle models[32–34]have been developed to study the collective cell motion in an epithelial sheet.It is found that both polarity-velocity alignment and locomotion interactions can affect the collective motion.Bi et al.[35,36]used a vertex model to describe the epithelial junctional and cortical tension rigidity transition in biological tissues.It was found that the onset of rigidity transition between liquid and solid was governed by a model parameter in confluent tissues.The self-propelled Voronoi(SPV)model was used to study the coherent motions in confluent cell monolayer sheets[37–39].A cell-based FE model[40,41]was adopted to study the wound healing process.In this model,the cell-cell adhesion was represented by the tension force tangent to the cell edge.The simulation studies implied that either cell crawling or purse-string contraction can lead to wound closure.Lin et al.[42]proposed an interfacial interaction model to study the collective epithelial cell migration behavior.Through the simulation,it reveals that the direction of cell movement is better aligned with the local principal stress direction at the higher maximum shear stress region.

Although the collective cell migratory behaviors in confluent tissues have been studied,the mechanisms of coordinated motion in cells are still unclear and controversial due to the following attributes:First,there are limitations in experimental studies to identify individual contribution factor in the collective cell migration behavior;Second,the lack of advanced continuum physics-based computational tools also make it difficult to uncover the collective cell migration mechanism.Models such as the vertex model and particle model are advanced models.However,they are not real continuum physics-based models.How the mechanical clues will influence the collective cell migration behavior is not very clear.The model could not capture essential features of cell mechancial property and the intercellular interaction at cell-cell junction between adjacent cells.So it is necessary to develop continuum physics-based collective cell model to bridge the knowledge gap between cell biology and cell biomechanics in a confluent monolayer.In this study,a collective cell model considering intercellular adhesion,cell-substrate adhesion and cell stiffness,is used to study the cell migration mechanism.An advanced computational model and finite element based simulation tool was developed to investigate how intercellular interaction and cell stiffness may affect the cell migration behavior.

2 Models and Materials

2.1 Geometric Model of the Epithelial Monolayer and Boundary Conditions

The epithelial monolayer is reported to be a thin layer of 3–15μm in thickness[43,44].For simplification,a 2D plane stress model of the epithelial monolayer was created using the Voronoi tessellation method to represent the monolayer sheet[35,45,46].Generally,polygon-shaped epithelial cells were first generated within a square region using the Centroidal Voronoi tessellation method.Then,cell-cell interfacial zone was generated to characterise the intercelluar interaction between adjacent cells.In this study,sixty-four(64)densely packed epithelial cells were created and the average cell size was set to be around 30μm,which is in the size range(10–36μm)of epithelial cells[47].The cell junction size was set to be 10 nm throughout the model,which was reported in literatures[48,49].Fig.1 illustrates the geometric configuration of the two-dimensional epithelial monolayer.The 64 cells in the simulation model are confined in the square box region,and the simulation box is fixed during the simulation.During the cell migration,the position of the centroid for each cell is updated,and thus the edges for each cell get updated.All cells are moving inside of the confined box.

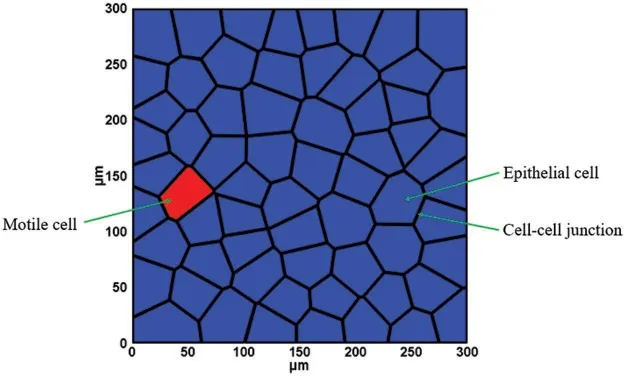
Figure 1:Geometry model of the epithelial monolayer sheet

2.2 Interaction Force Modeling

2.2.1 Intercellular Interaction Modeling at Cell-Cell Junction

The transmission of mechanical forces is broadly recognized to play a significant role during cell migration processes.While the motile cells move,they will interact with their neighboring cells,and the interaction force will be transmitted through cell-cell junctions[50].Mechanical stresses exerted at cell-cell junctions have been studied in experiments with different measurements[51–54].In experimental studies,the intercellular adhesion within a migrating monolayer can be decomposed into normal traction that is perpendicular to the cell-cell junction and shear traction that is tangential to the cell-cell junction as shown in Fig.2.

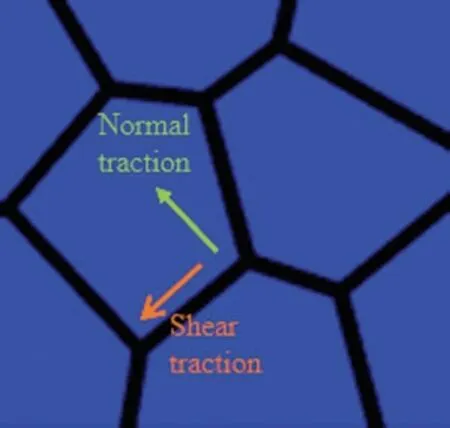
Figure 2:Intercellular interaction at cell-cell junction

Some computational frameworks such as the vertex model and cellular potts model have been developed to study the collective cell migration processes[29,35].These models incorporate the contribution of the intercellular adhesion,however,they are pure mathematical models that could not capture the mechanical behavior of the cell tissue.In this study,the intercellular interactions at cell-cell junctions were modeled using an interfacial interaction model which was proposed by Lin et al.[42]to investigate the collective epithelial cell migration,and it takes the following forms:

The traction-separation laws used to model the intercellular interaction is illustrated in Fig.3.This model has been employed to describe intercellular interactions in collective cell migration and in other biological material modelings[42,55].

The critical intercellular interaction distance in both normal and tangential directions,δdnandδdtin our model,were estimated as 1μm.The interaction cutoff distance in normal and tangential directions,δfnandδft,were set as 2μm.The intercellular adhesion strength in both normal and tangential directions,σc-candτc-c,were approximated as 2 nN/μm2since the cell-cell adhesive traction were in a range of 1 ～8 nN/μm2measured by Liu et al.[56].Theqnandqtdescribe the exponential behavior in the normal and tangential direction respectively,and were set to be one for simplificity.Thepnandptdescribe a type of linear detachment progression between adjacent cells when the intercellular separationdnordtexceedsδdnandδdtin the normal and tangential direction,respectively.Thepnandptwere set to be one for simplificity in current study.

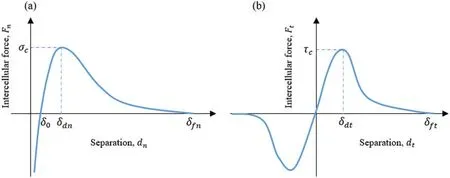
Figure 3:Intercellular interactions at cell-cell junction:(a)Normal direction,(b)Tangential direction

2.2.2 Cell-Substrate Adhesion Modeling

Cell movement also invloves cell-substrate adhesion which is the attachement of a cell to the underlying substrate through mechanosensitive focal adhesion complexes of the integrin family[57].It enables cell activity in the extracellular matrix to affect the cell shape and movement.There have been many efforts on the modeling of cell–substrate interactions[58–61].An exponential cohesive zone model[62]was employed to represent the cell–substrate interfacial behavior[60].The normal traction of the cell–substrate adhesion can be ignored according to previous analysis[63].Therefore,we only consider the cell–substrate adhesive traction in xy plane for simplification in this study,and it takes the following form:

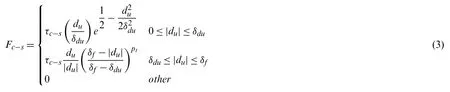
In the above equation,τc-srepresents the maximum cell-substrate adhesion strength.In this study,τc-swas set to be 5 Pa according to the previous experimental measurement[63].Theduis the separation distance between the cell and the substrate.The critical interaction distanceδduis the distance between the cell and the substrate when cell-substrate adhesion reaches its maximum value,which was set to be 25 nm according to previous study[60].The detachment distanceδfis estimated as 60 nm according to the reported measurements[64,65].

2.2.3 Protrusion Force Modeling

In the protrusion-based cell migration,actin polymerization leads to the formation of protrusions that adhere to the surrounding extracellular matrix(ECM).Then the formed protrusions retract,resulting in cell movement along the cell path[66,67].Cell migration is a dynamic process that is highly regulated by complex biological cues[68].The formation of protrusion generates protrusion forces at the leading edge of the motile cell that could empower cell movement.The value of traction force on leading edge ranges from 0.25 to 3 nN according to the previous experimental studies depending on different measurement methods[69,70].In addition,it is shown that each cell in an advancing epithelial monolayer was also involved in a global tug-of-war[63].Therefore,in this study,one cell located at far left of the box was selected as the motile cell(Fig.1),and a 2 nN protrusion force was applied on the motile cell along the x-axis direction.The protrusion forces on edges of all other cells were applied along random directions in the range of 0–0.3 nN.

2.3 Material Properties

In this study,the epithelial cell was assumed as an isotropic elastic material and the Young’s modulus was set at different values between 0.3 and 30 KPa,and Poisson’s ratioν=0.45 according to the measurements reported in previous experiments[71,72].The mass density was set to be 2×10-3ng/μm3for individual epithelial cell according to the previous measurements[73,74].In the curent cell modeling,we did not model the detailed cell internal microstructures.

3 Finite Element Implementation

In this study,a displacement-based finite element formulation was developed.The Galerkin weak formulation of the compuational model that neglects the body force during the deformation can be represented by the following terms:

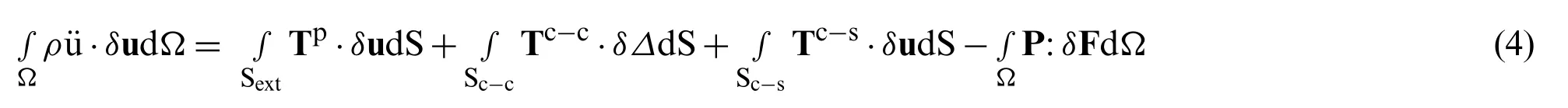
whereρis the material density of the cell,Ωis the volume,Sextis the cell external surface,Sc-cis the cell-cell junction surface,Sc-sis the cell-substrate surface.Tpis the protrusion traction vector,Tc-cand Tc-sare the intercellular interaction traction vector and cell-substrate interaction traction vector,respectively,P is the first Piola-Kirchhoff stress tensor,and P:δF=PijδFji.The descrete equations of motion can be expressed by following forms:

In the above equations,M is the mass matrix,Fextis external force which is consitituted of protrusion force Fp,intercellular interaction force Fc-cand cell-substrate adhesion force Fc-s.Fintrepresent the internal force resulting from the epithelial cell deformation.

4 Simulation Results

Numerical simulations were performed to investigate the cell migration behavior in a confluent epithelial monolayer.All simulations were conducted by using a custom-designed finite element package using Fortran,which was developed by Lin et al.[42].

4.1 Stress Distribution in Epithelial Monolayer Sheet

In the finite element simulation,each cell in the monolayer sheet was discretized into linear triangle elements to perform the computation.At each nodal point,the maximum and minimum principal stresses were calculated according to the following formulation:

Then the average local normal stress is computed asσave=(σmax+σmin)/2 and the maximum shear stress is computed asτmax=(σmax-σmin)/2.Fig.4 shows the contours of the average local normal stress and the maximum shear stress while the motile cell migrates from the left to right with cell stiffness of 0.3 KPa.It can be seen that the value of the average local normal stress is greater than the value of the maximum shear stress in the motile cell.These observations were consistent with experimental studies[54,75],some other studies reported comparable amount of shear stress obtained through experiments[51,63].To visualize the entire migration process,one cell located at far left of the box was selected as the motile cell.The motile cell migration in the monolayer can be seen in movie S1.All other cells are migrating with very small displacement compared to the motile cell since the protrusion force applied on the motile cell is larger than the rest of the cells.In our current study,the cell extrusion is not considered.When the maximum stress in the cell monolayer reached a predefined threshold value,cell remodeling will start and cells will change their shapes during the migration process.Cells may change their neighbors after cell remodeling.The cell density is maintained during the collective cell migration process.

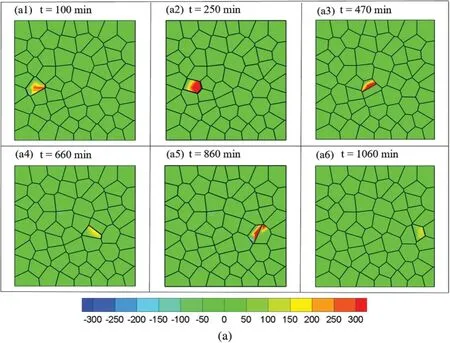
Figure 4:(Continued)

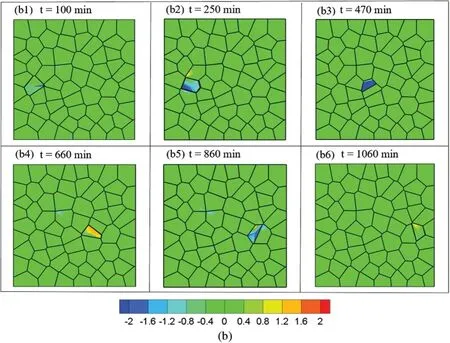
Figure 4:Stress distribution at different time step while the motile cell migrates from left to right:(a)Contour of average normal stress and(b)Contour of average shear stress at different time step:t=100 min,t=250 min,t=470 min,t=660 min,t=860 min,t=1060 min

Then we plot the effective stress in the epithelial monolayer sheet in Fig.5.It can be seen that the stress in the motile cell is several orders higher than stress in other cells.

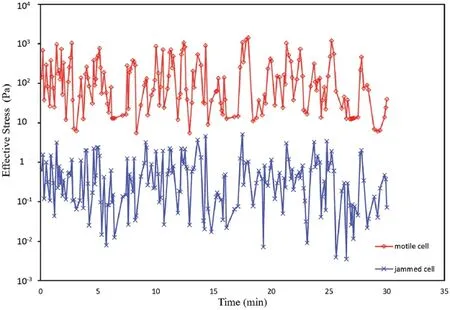
Figure 5:Effective stress in the motile cell and the jammed cell

4.2 Contribution of the Cell Stiffness on Cell Migration Behavior

Cell stiffness has been identified as an important mechanical property that influences cell motility and cell migration behavior.Many experimental studies have shown that higher cell motility often relates to lower stiffness,which might favor cell migration,epithelial-mesenchymal transition in many biological activities[25,26,76–79].However,some conflicting evidence has been reported that cancerous cells with higher motility are stiffer than their benign counterparts[80,81]that makes the relationship between cell stiffness and cell motility still a controversial topic.The value of epithelial cell stiffness has been reported in a range from 0.1 to 20 KPa depending on different cell types and measurements[72,82].To computationally explore the effects of cell stiffness on the cell migration behavior,in this study,all the parameters were kept the same except the stiffness was set to be 0.3,3,10,20 KPa respectively for different cases.The displacement of the motile cell verses time during the migration is plotted in Fig.6.It can be seen that higher stiffness results in smaller displacement and lower migration speed.This result is consistent with previous studies[25,26,76–79]since low cell stiffness often associated with higher ability to deform,therefore leads to higher motility.

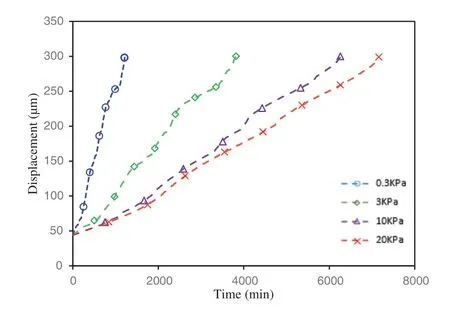
Figure 6:Displacement of the motile cell during the migration processes with different cell stiffness

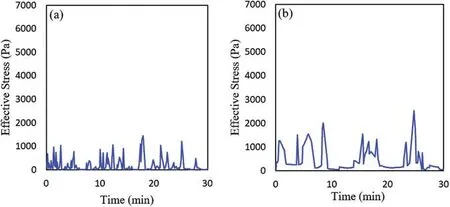
Figure 7:(Continued)

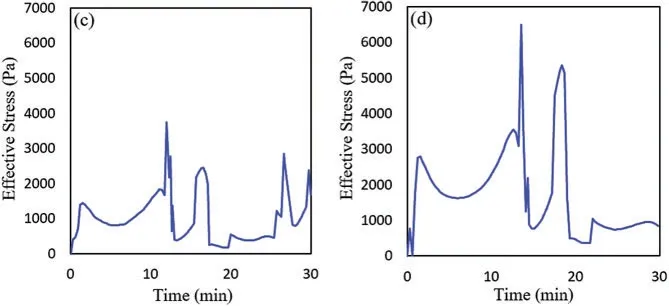
Figure 7:Effective stress vs.time in the motile cell with differnet cell stiffness:(a)E=0.3 KPa,(b)E=3 KPa,(c)E=10 KPa,(d)E=20 KPa

Then we plotted the effective stress in the motile cell during the cell migration for all four cases with different cell stiffness as shown in Fig.7.One might see that higher stiffness leads to higher stress in the cell which is consistent with recent experimental studies[27,83,84].

5 Discussions and Conclusions

In this study,a continuum physics-based computational model including the intercellular interaction was employed to study the cell migration behavior in a confluent epithelial monolayer.The epithelial layer was modeled as an isotropic elastic material.Through finite element simulation,the results revealed that the motile cell was subjected to higher stress than other cells during the migration process.And our results showed that the normal intercellular interaction dominates over the tangential intercellular interaction.Cell stiffness was indicated to play a significant role in cell migration behavior,higher stiffness results in smaller displacement and lower migration speed.When transiting from the quiescent state to the motile state,the traction force in epithelial cell may decrease in order to escape from the collective cells.The simulation model-based study may provide possible explanations and insights on how the mechanical cues affect the cell migration behavior.

It should be noted that cell migration is a complex biological phenomenon,and there are several limitations associated with the presented study.Firstly,a 2D plane stress model was used for simplification in this study,which might not fully represent the 3D cases.Secondly,the epithelial cells were modelled as the simple isotropic material which does not consider the detailed cell microstructure and the complex cell material properties.Thirdly,the presented computational model does not take into account of the factors such as “chemotaxis” or “durotaxis” in cell movements,so the protrusion force applied may not be realistic in real situation.Only one cell is selected as motile cell in the current study.In our previous cell migration study,we investigate how the number of self-propelled monocytes affected the collective migration behavior as a group.It was found that more self-propelled cells are in the system moving along the same direction,the faster the collective group migrates toward coordinated direction[85].In our future study,we plan to build cell model with internal microstructures by using liquid crystal and liquid crystal elastomers,and to build a 3D epithelial cell migration model to further investigate the role of mechanical interaction on the cell migration behaviors.

Funding Statement:This work is supported by a grant from National Institutes of Health(Grant No.SC2GM112575)and a grant from the John L.Santikos Charitable Foundation of the San Antonio Area Foundation.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.