斜侵彻靶板过程中装药损伤的数值模拟

毕 超，郭 翔，屈可朋，沈 飞

(1.天津大学 机械工程学院，天津 300354；2.西安近代化学研究所，陕西 西安 710065)

引言

在含炸药装药的炮弹侵彻靶板过程中，较高的过载和复杂的应力波作用会对装药的性能产生极大影响。Barua等[1]发现通过微结构的整体波速取决于晶粒的体积分数和晶粒-黏结剂的界面强度。李媛媛等[2]数值模拟了含装药的炮弹斜侵彻混凝土靶板，发现装药的前端主要受压缩作用，而后端受到拉伸与压缩的共同作用。石啸海等[3-4]发现垂直侵彻后在装药内部出现了垂直于轴向的裂纹，同时，头部缓冲层会降低装药的最大裂纹宽度和宏观裂纹数量，而增大弹头的形状系数会使侵彻后装药内部可见裂纹的含量出现整体下降和局部上升的趋势。Li等[5]研究了垂直侵彻过程中PBX的力学行为，实验发现装药从尾部到中部都含有损伤区域，数值模拟的结果表明装药在侵彻过程中反复经历压缩与回弹造成装药尾部及中部的严重损伤。

总体来看，关于斜侵彻情况下装药损伤的研究较少。内聚力模型从虚功原理出发，借助于拉力—张开位移关系，利用实验或从更小尺度模拟得到的内聚参数，能在细观和宏观尺度直接模拟损伤的起始和演化。因此，本研究基于内聚力模型对含装药的炮弹斜侵彻多层靶板进行了模拟，分析与量化了装药裂纹区，并与试验结果进行了对比。基于验证的模型，开展了靶板后倾角度与装药损伤关系的研究，发现后倾角度的变化会导致裂纹区的出现位置及演化过程发生变化，从而导致宏观裂纹与装药横向的夹角发生变化。

1 有限元模型

1.1 几何模型

弹-靶的基本模型如图1所示，包含靶板、弹体、缓冲层、装药和隔板5部分。炮弹的外部直径为51mm，长径比约为5.1，弹头形状系数为2.6，后盖厚度为12mm，壳体厚度为5mm。缓冲层厚度为10mm。靶板层数为3层。装药用隔板分成5块(从头部到尾部编号分别为1～5)，长度分别为18、40、40、40和47mm，隔板厚度为0.5mm。同时，选择在装药轴向的实体单元之间横向界面处全局插入内聚力单元作为裂纹萌生的位置与扩展的路径。

图1 弹-靶模型示意图

1.2 材料模型

靶板、缓冲层和弹体分别为45号钢(密度为7800kg/m3，泊松比为0.33，弹性模量为210GPa)、聚碳酸酯(密度为1190kg/m3、泊松比为0.38，弹性模量为3.6GPa)和35CrMnSi钢(密度为7830kg/m3，泊松比为0.3，弹性模量为204GPa)，采用Johnson-Cook塑性本构模型描述其在不同的温度和应变率下的力学性能：

(1)

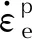
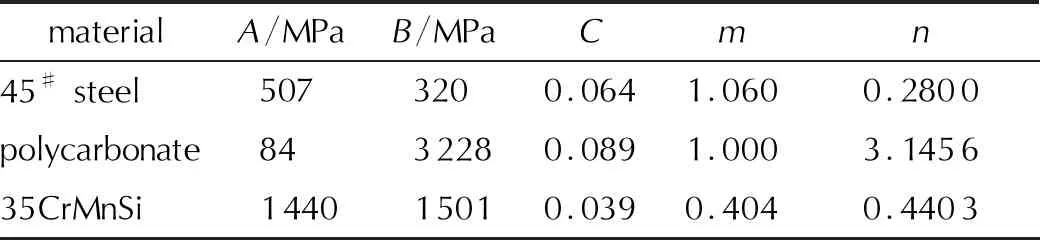
表1 材料参数[6-8]

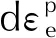
(2)

式中：εf是失效应变，通过式(3)进行定义：

(3)

式中：d1～d5为材料常数，分别为0.10、0.76、1.57、0.005和-0.84；p为静水压力。

隔板为硅橡胶，采用弹塑性模型，密度为1190kg/m3，屈服强度为100MPa，剪切模量为1.78GPa[9]。同时，不考虑缓冲层、弹体和隔板的损伤行为。

由于高应变率，PBX装药采用弹塑性模型，密度为1850kg/m3，泊松比为0.3，弹性模量4.5GPa，屈服强度49MPa，硬化模量为1GPa[10]。内聚力单元采用双线性拉力—张开位移关系，可以表示为：

S=(1-d)·k·δ

(4)

式中：S为拉力；δ为张开位移；k为内聚力单元初始刚度；d为损伤因子。

采用最大名义应力准则来定义损伤的起始。当拉力达到内聚强度时，损伤发生。之后，随着张开位移的增加，在其达到失效位移之前，损伤因子d从0单调增加，直到达到失效位移时，d增加到1，内聚力单元完全损伤，出现裂纹。断裂能为284J/m2[9,11,12]，δm为失效位移，具有长度量纲，计算公式如下：

δm=2·G/S0

(5)

式中：S0代表内聚强度，约为7.6MPa[13]。

2 结果与讨论

2.1 装药过载与损伤机理

试验采用高压气室形成的高压发射含装药的炮弹，炮弹布设于靶板正前方。计算采用与试验一致的参数，炮弹速度为400m/s，三层靶板厚度均为15mm，后倾10°，间距为300mm。

炮弹斜侵彻靶板的过程中，装药除了承受轴向阻力的作用还会受到横向阻力的作用。提取装药的所有点的轴向和横向过载数据分别做平均，输出过载曲线如图2所示。由图2可以看出，其轴向与横向过载峰值都出现在炮弹侵彻第一层靶板的过程中，分别约为9.62×104g和4.41×104g。同时，炮弹击穿靶板后，其轴向受力首先减小，横向依然会受到较大阻力的作用，导致横向过载峰值的出现时间滞后于轴向过载峰值的出现时间。

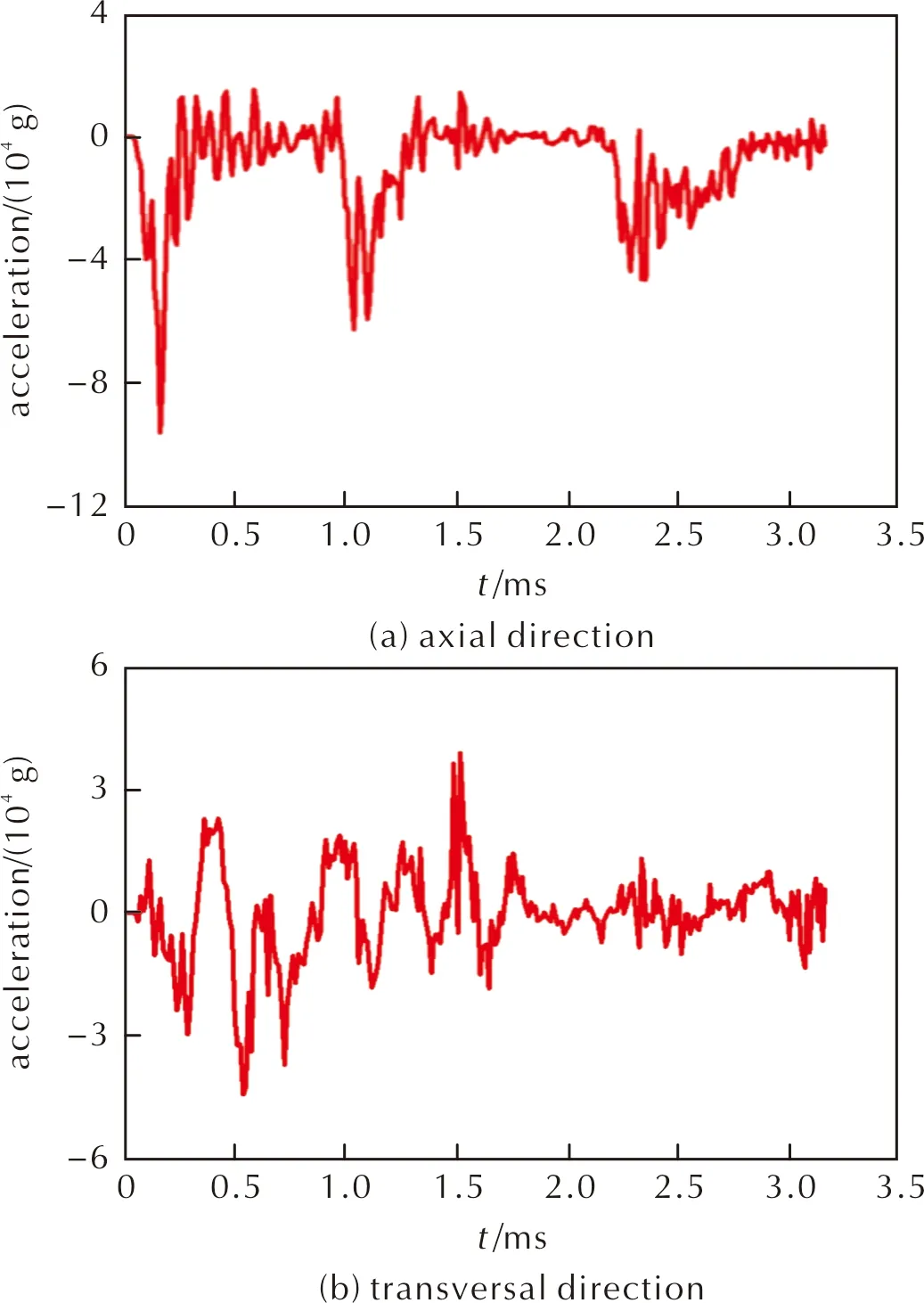
图2 装药轴向方向和横向方向的过载曲线

当内聚单元的SDEG达到1时，单元完全损伤，出现裂纹。图3给出了装药裂纹区的演化过程。

图3 装药裂纹区的演化过程

裂纹最先出现在装药尾部的两侧，随着时间的增加，裂纹区同时向尾部端面和头部两个方向进行演化。将SDEG值达到1的内聚力单元数目与总内聚力单元数目的比值定义为装药的损伤区占比。大约在4.5ms左右，炮弹完全击穿三层靶板，损伤区占比约为34.6%。编号5装药基本完全损伤，编号4装药部分位置也出现了裂纹区。注意，缓冲层与弹体部分没有定义损伤，所以没有SDEG值。

当炮弹撞击靶板时，会在头部产生相对较短时间的高幅值脉冲载荷，脉冲载荷以压缩波的形式向尾部传播。因为弹体与装药材料不同，只有部分压缩波传入装药，并朝装药的尾部继续传播。压缩波到达装药尾部之前，装药基本不会发生太大的损伤。同时，由于惯性作用，装药会向头部挤压，使得尾部与弹体之间产生间隙，形成自由面。压缩波传播到尾部自由面时会反射形成拉伸波，当拉伸应力大于装药的内聚强度后，开始萌生裂纹。拉伸波传播时，到达自由面(包括尾部自由面和裂纹自由面)或者界面后反射回压缩波，反之亦然。装药不断地经历压缩与拉伸的过程，引起裂纹的闭合与进一步扩展，最终导致装药内部有的裂纹形成宏观裂纹。

同时，斜侵彻情况下，横向过载的出现及不断变化导致裂纹区的出现及演化并非垂直于轴向。因此，选择将裂纹区出现位置所在的斜截面作为宏观裂纹进行量化。图4是量化后的宏观裂纹的位置。由于拉伸波在装药的尾部反射，所以靠近尾部位置的装药的损伤相对较为严重。因此，量化后宏观裂纹的靠近尾部端面一侧的装药为严重损伤区，远离尾部端面的一侧为轻微损伤区。远离靶板侧，宏观裂纹距离装药尾部约为28mm，而靠近靶板侧，距离装药尾部约为4mm。宏观裂纹与装药横向的夹角约为30°。

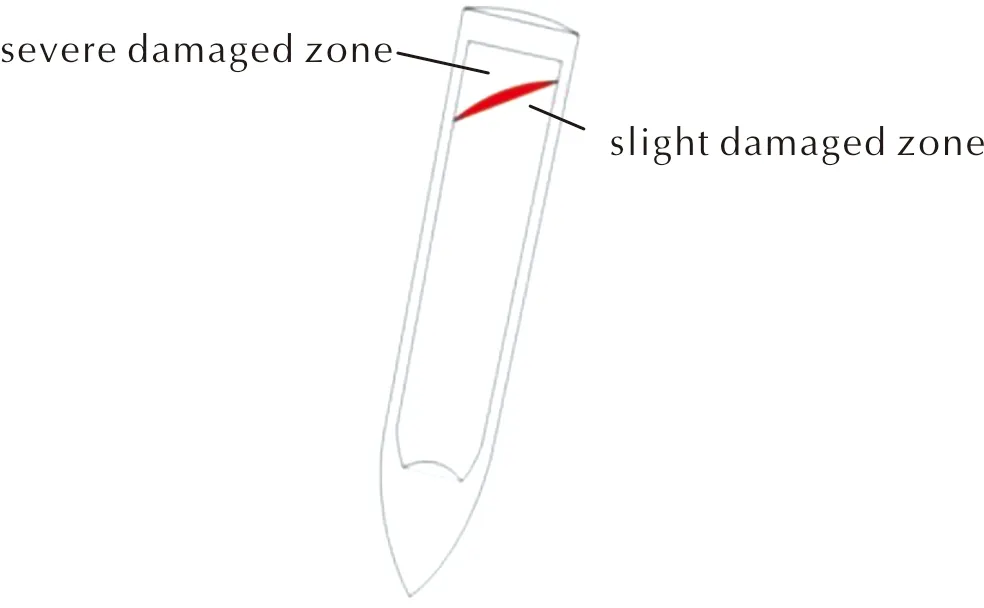
图4 量化后的宏观裂纹

2.2 量化的损伤区结果与试验结果的对比

在图4距离装药尾部19mm和26mm的位置分别截取横截面，如图5所示。红色区域为严重损伤区，距离尾部19mm和26mm截面的严重损伤区面积约为截面面积的14.1%和0.7%。

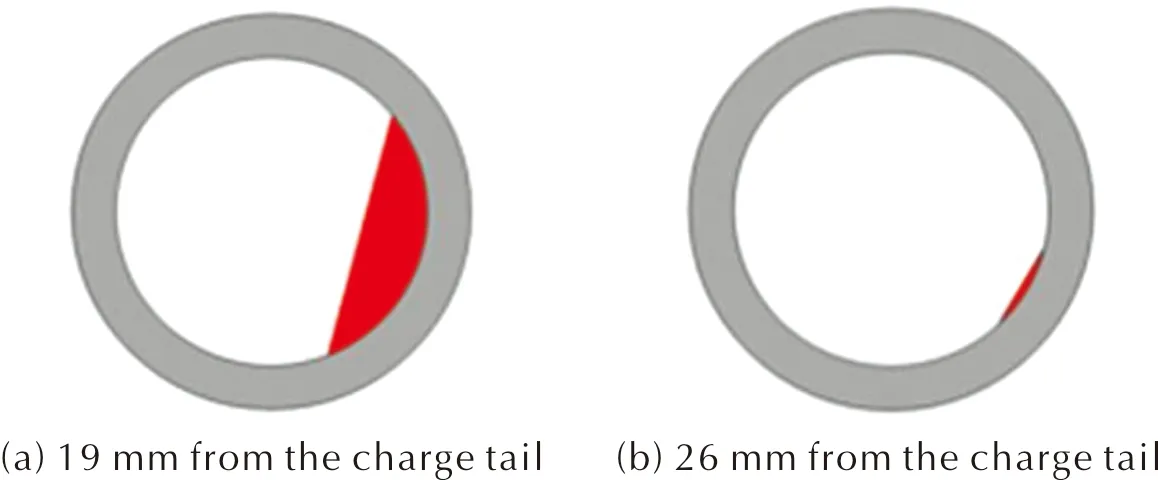
图5 量化区域的横截面

图6给出试验结果两个位置的横截面图。距离装药尾部19mm的截面显示出较大部分的装药损伤严重，包含大量的微裂纹；而距离尾部26mm的截面则显示出一小部分的装药已完全破坏，出现了大量微裂纹。将图5与图6进行对比，可以发现模拟与试验结果较为吻合，保证了后续模拟的准确性。侵彻试验结果的影响因素(如实验装置偏差和材料细观非均匀性等)较多，而数值模拟过程较为理想化，所以模拟结果与试验结果很难完全一致。

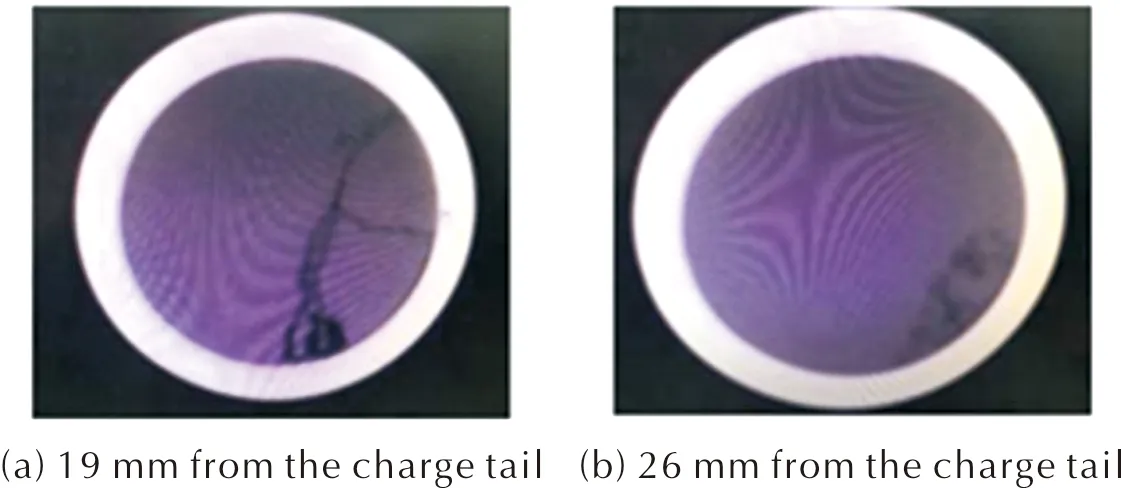
图6 试验结果的横截面

2.3 靶板倾角对装药损伤的影响

改变靶板的倾角，设置靶板后倾的角度分别为5°、10°、15°和20°，靶板厚度为12、7和7mm，装药不添加分隔板，其他模型参数保持不变。

图7、图8和图9分别给出了侵彻过程中装药的过载曲线、速度曲线和裂纹区分布。表2汇总了计算结果。相对于后倾5°，后倾20°时装药的轴向过载峰值约提高了0.62×104g，即8.5%；横向的过载峰值约提高了1.35×104g，即221.3%。横向过载的增大说明装药的横向受力增大，这也导致宏观裂纹与横向的夹角发生变化。从后倾5°到20°，装药的剩余速度从251m/s降低到207m/s，下降了44m/s，约为后倾5°时的17%，但是装药的损伤占比基本不变。这是因为倾角变大之后，炮弹与靶板的接触面积变大，装药的受力增大，耗散的动能增加，速度下降明显。

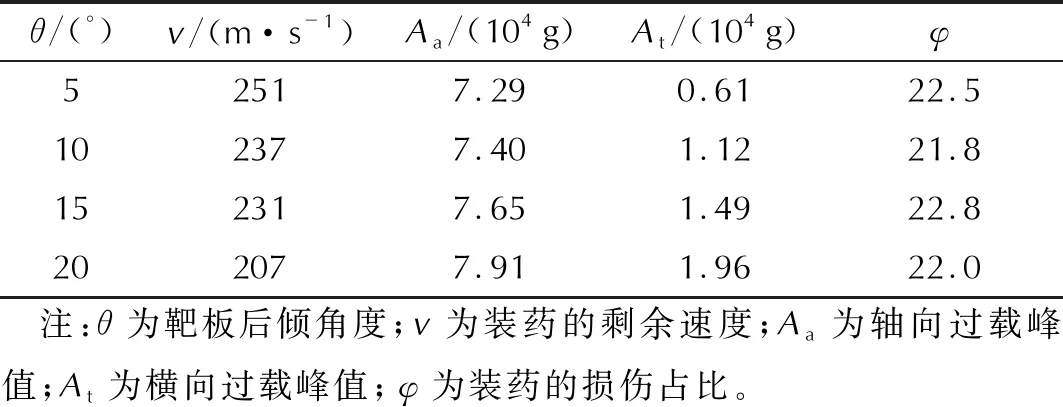
表2 不同倾角下剩余速度、过载和损伤占比

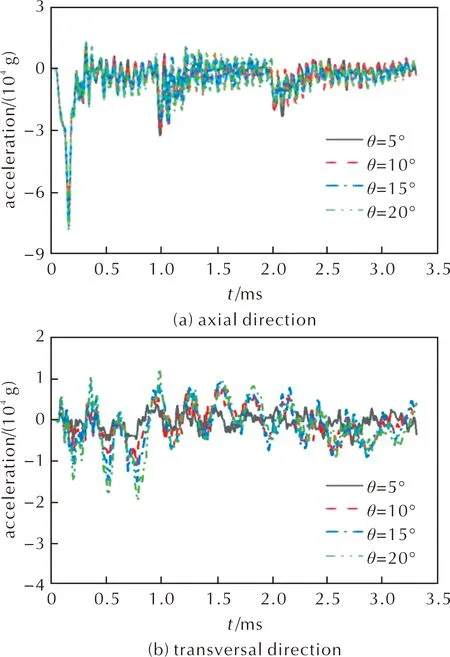
图7 不同倾角下装药轴向方向和横向方向的过载曲线

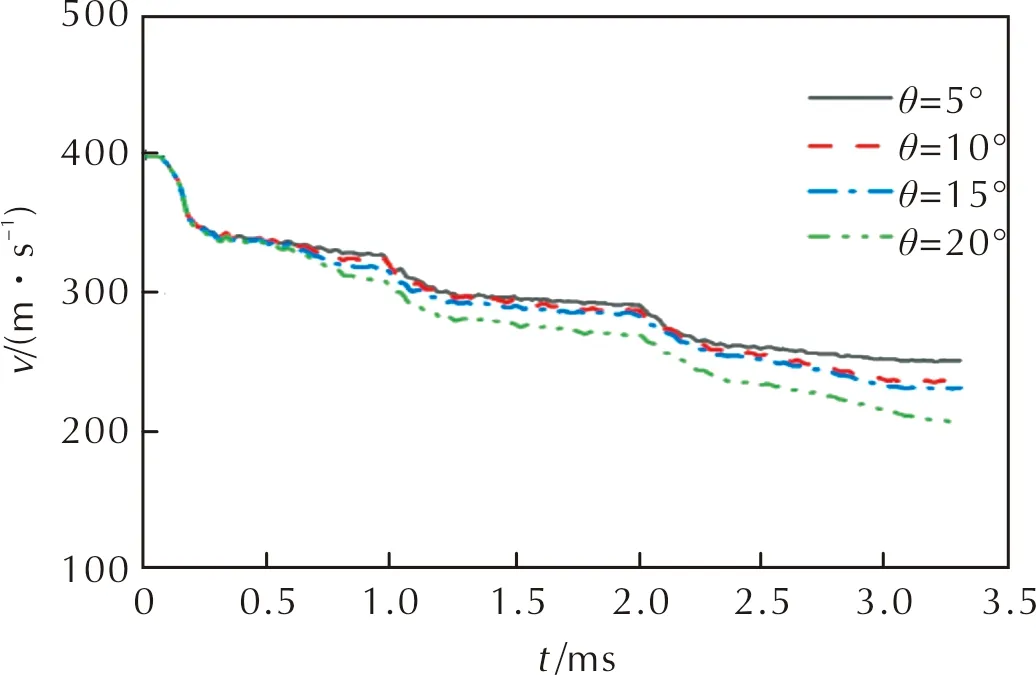
图8 不同倾角下装药的速度曲线

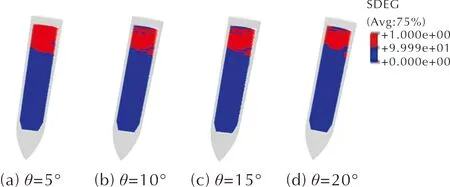
图9 不同倾角下装药的裂纹区分布

图10给出了不同靶板倾角下装药裂纹区的出现位置。对裂纹区进行量化后发现，后倾5°、10°、15°和20°时，远离靶板侧，宏观裂纹距离装药尾部分别约为28、30、32和34mm；而靠近靶板侧，宏观裂纹距离装药尾部分别约为8、6、4和4mm；宏观裂纹与装药横向的角度分别约为26°、30°、34°和36°。即，随着靶板后倾角度的增大，量化后的宏观裂纹与装药横向的夹角不断增大。

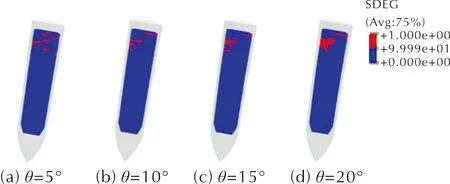
图10 不同倾角下装药裂纹区出现的位置

3 结 论

(1)基于内聚力模型，模拟了含装药的炮弹斜侵彻多层靶板过程中装药的损伤行为，提取了装药的过载和速度等重要结果，分析了裂纹的出现及演化。结果表明，压缩波到达尾部自由面反射回拉伸波是导致裂纹出现的主要原因，压缩与拉伸的反复作用导致了裂纹演化。

(2)斜侵彻过程中，炮弹要承受轴向阻力和横向阻力的共同作用，导致裂纹区的出现与演化不再垂直于装药轴向，而与横向成一定角度。

(3)装药的最终裂纹区的量化结果与实验结果吻合良好。同时，随着靶板后倾角度的增大，装药的横向过载会增大，导致量化后装药的宏观裂纹与横向的夹角增大。