面向直升机抗坠毁的新型夹心八边形蜂窝设计、仿真和理论研究

王佳铭，李志刚,*，梁方正，刘婉婷，廖就，陈芳育，李萌，邵特立

1.北京交通大学 机械与电子控制工程学院，北京 100044

2.中国直升机设计研究所，景德镇 333001

3. 中国空间技术研究院 钱学森空间技术实验室，北京 100094

4. 交控科技股份有限公司，北京 100070

蜂窝结构作为多孔结构的一种，由于其密度小、刚度低、压缩变形大及变形可控等优点，现已成为一种理想的缓冲吸能结构，目前广泛应用于汽车、轨道交通和航空航天等领域。在实际的工程应用中，很多实际场景对蜂窝的承载吸能能力要求很高，例如直升机的耐坠性设计等碰撞动能较大的相关领域，这些场合下需要具有更高吸能能力的新型蜂窝以在相同的安装空间或同等质量条件下吸收更多的坠撞动能，保障乘客的生存空间。基于此，本文提出了一种相对于六边形和正方形蜂窝结构吸能效果更好的新型蜂窝。

目前在对蜂窝结构的研究中，首先是理论层次的研究，国内外部分学者针对多种常用构型的蜂窝力学承载进行了理论模型的推导建立，其中荣吉利、Bai等给出了六边形蜂窝轴向平台应力的理论公式，为蜂窝结构缓冲设计提供理论依据。在蜂窝结构的尺寸参数影响方面，大部分学者通过仿真与试验相结合的方式，对六边形蜂窝胞元尺寸参数(边长、壁厚等)以及蜂窝块尺寸参数(长、宽、高)对蜂窝力学性能的影响展开研究。其中赵辉等研究表明蜂窝压缩时平台应力等力学性能指标与壁厚边长比值正相关，徐天娇、贾培奇等研究表明，面内尺寸及高度变化时，平台应力没有明显的尺寸效应，但密实化应变对高度尺寸具有一定敏感性。此外，在蜂窝压缩仿真方法的研究方面，欧阳昊、王永宁等发现壳单元有限元模型能准确反映铝蜂窝逐步压溃的变形模式，车全伟等也提出了一种合理的蜂窝压缩仿真建模方法。

近些年来，有学者开始将研究聚焦在新型蜂窝结构的设计，以求获得吸能效果更佳的蜂窝结构。何彬和李响提出了一种基于菱形和圆形的新型组合蜂窝，通过数值仿真与正六边形、正方形、三角形、Kagome 蜂窝的中高速冲击仿真结果进行了对比，发现新型组合蜂窝整体刚性和能量吸收能力较好。王中钢和姚松对加筋型正六边形蜂窝进行了轴向压缩力学性能的研究，结果表明1.5 倍厚度加筋的蜂窝力学性能稳定，是最优的筋厚选择方案。Yang等的研究表明，在传统蜂窝结构基础上引入马蹄形结构或混合波纹结构后，蜂窝平台应力和比吸能都有一定程度的增强，李萌等通过仿真试验相结合的方式，发现串联组合式铝蜂窝缓冲器相较于单个铝蜂窝缓冲器来说可以吸收更多能量。

本文基于正方形蜂窝和八边形蜂窝提出了夹心八边形新型构型蜂窝，首先通过六边形蜂窝轴向压缩试验和仿真对比，验证了蜂窝建模和仿真方法的正确性；然后建立了不同尺寸的八边形蜂窝有限元模型并进行了变形模式和吸能的分析，并对夹心八边形蜂窝和常用的六边形蜂窝等进行了吸能能力的对比分析；最后建立了夹心八边形蜂窝的理论模型并进行了仿真验证，表明建立的理论模型对蜂窝的平台应力以及相对密度具有很好的预测精度，为新型蜂窝缓冲结构的设计提供了依据。

1 夹心八边形蜂窝设计

为了进一步提高蜂窝结构轴向吸能能力，本文设计了夹心八边形蜂窝结构，以正八边形蜂窝胞元为出发点，采用内嵌四边形蜂窝以填充胞元内空隙，以合理的相对密度增加将新构型蜂窝的承载吸能效果更大化。正八边形蜂窝胞元边长为，内嵌四边形蜂窝胞元边长为，并在之间添加肋板连接形成夹心八边形蜂窝，整个结构的壁厚均为，阵列获得最后所需结构，其中标红部分为该构型的一个基本可重复单元，如图1所示。

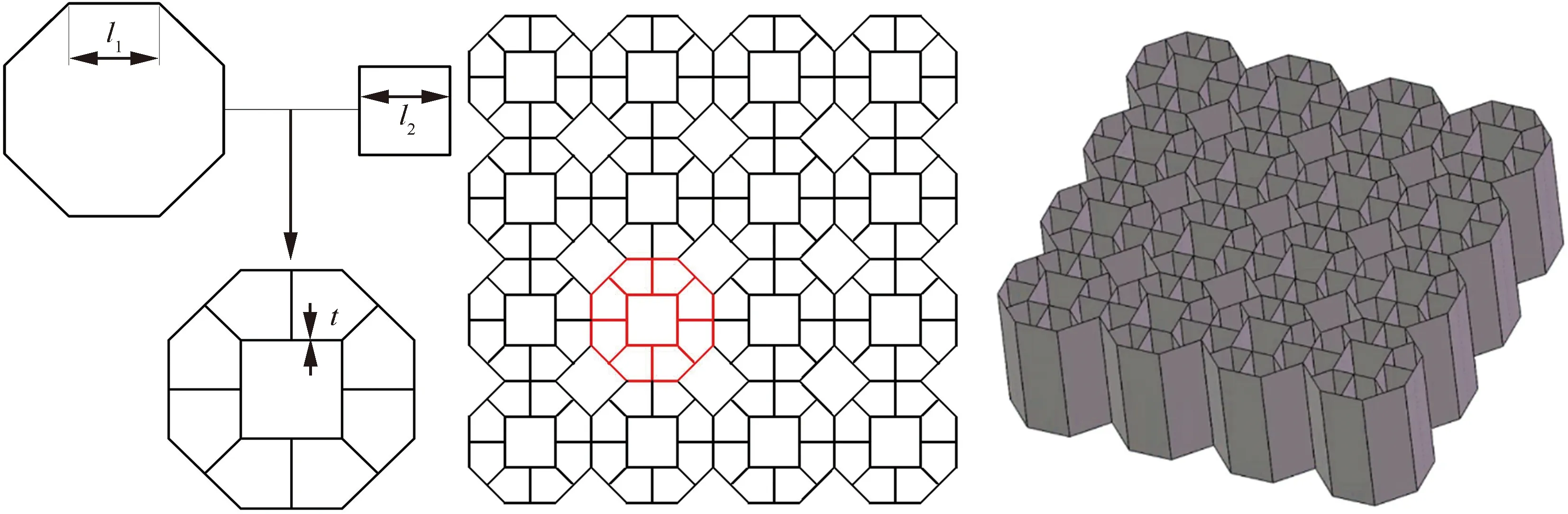
图1 夹心八边形蜂窝设计Fig.1 Design of cored octagon honeycomb

2 夹心八边形蜂窝理论模型

考虑到通过仿真或者试验的方式来研究夹心八边形蜂窝承载能力计算周期较长，因此本节将建立夹心八边形蜂窝轴向承载时的平台应力的理论模型以快速预测该构型轴向压缩时平台应力等吸能指标随参数的变化规律。

2.1 平台应力理论模型

蜂窝在承受轴向压缩时，经历3个阶段，首先是线弹性区域，应力随应变线性变化，且快速增加至初始峰值应力；然后是平台区域，应力值围绕平台应力上下波动；最后是密实化变形区域，应力从密实点快速上升，进入密实化阶段。其中平台区通过发生周期性的折叠变形吸收能量，是蜂窝吸能缓冲的最重要阶段，通常占据蜂窝整体吸能的80%以上。平台应力是表征蜂窝结构吸能特性的一个重要指标。因此，本文推导建立了夹心八边形蜂窝平台应力的理论模型。本文提取图1中所示的夹心八边形蜂窝结构的一个基本单元进行分析以建立夹心八边形蜂窝的平台应力理论模型。根据Chen和Wierzbicki提出的超简化折叠单元理论，认为在其变形过程中，变形能由铰链屈曲吸能和膜延展吸能两部分组成。简化后的基本折叠单元如图2所示。

以一个塑性铰波长为2高的十字胞元为例，根据系统的能量守恒有

·2=+

(1)

式中：为平均压溃力；为铰链屈曲吸能；为膜延展吸能。

铰链屈曲吸能表示所有塑性铰链线弯曲变形能量总和。每个折叠单元由3条塑性铰线组成，如图2(a)所示，3条水平塑性静态绞线分别位于基本折叠单元的两侧和对折线上，相应旋转角度为π/2、π/2、π， 因此弯曲吸能可以表示为

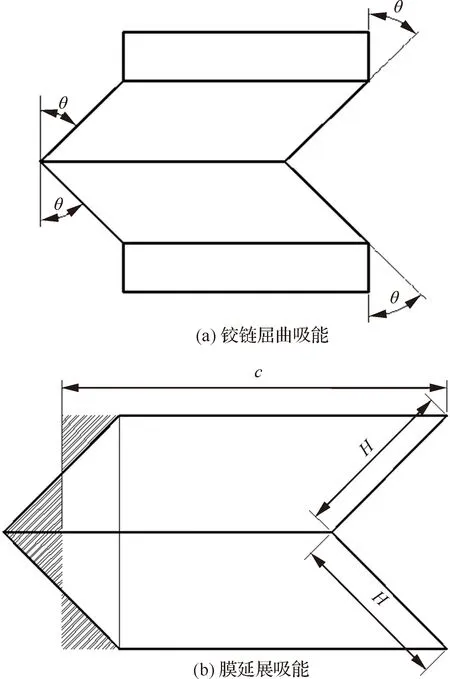
图2 超简化折叠单元Fig.2 Simplified super folding element

(2)

式中：为厚度为单元的全塑性弯矩；为每条绞线的旋转角度；为图2(b)中每条绞线的长度。对于厚度为的单元，=4，为流动应力，具体计算式为

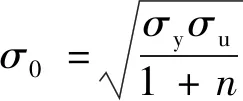
(3)

其中：为屈服应力；为极限应力；为材料硬化常数，取值为0.07。

将各变量代入式(2)计算得到夹心八边形蜂窝的铰链屈曲吸能为

=2π

(4)

式中：为夹心八边形蜂窝所有胞壁的二维截面长度。

为了分析夹心八边形蜂窝轴向压缩时的膜延展吸能，将其截面划分为3种基本单元：角单元、Ⅰ型三面板单元和Ⅱ型三面板单元，如图3所示。这3种基本单元的膜延展吸能是通过对图2(b)中阴影区域进行积分得到的。

图3 夹心八边形蜂窝截面的吸能单元划分Fig.3 Division of energy absorption unit of cored octagon honeycomb cross-section

根据文献[5]对两面板角单元的研究结果，通过对角单元拉伸和压缩区域进行积分获得膜延展吸能，计算式为

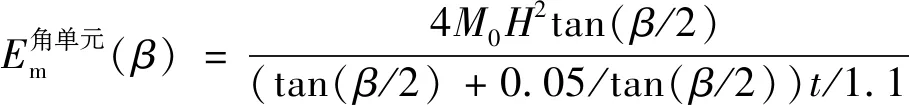
(5)

一个折叠波长高度的Ⅰ型三面板单元如图4(a) 所示。设对称面板的两个相同角度为，三面板单元的膜延展吸能应该包括一个两面板角单元和附加面板的膜延展吸能两部分，根据图4(b) 所示的附加面板的塌陷变形，三角形通过路径延展为三角形，文献[4]研究结果表明，附加面板的变化过程可简化为

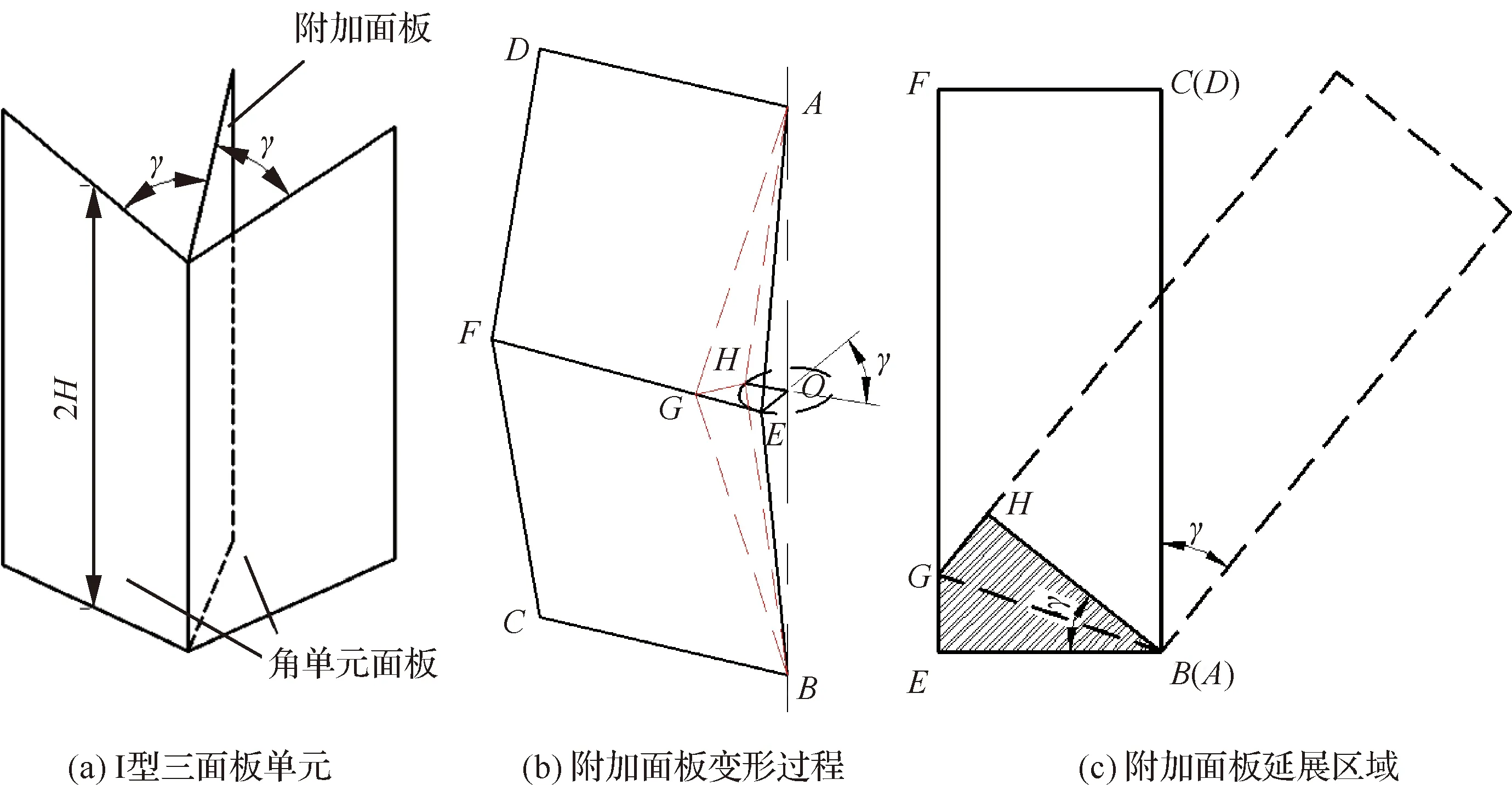
图4 Ⅰ型三面板单元变形过程Fig.4 Deformation process of three-panel angular element Ⅰ

图4(c)所示，两个阴影三角形区域被定义为拉伸区域，对其进行积分可以得到附加面板的膜延展吸能，表达式为

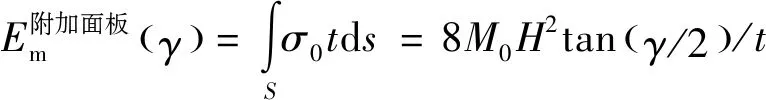
(6)

式中：为阴影部分的面积。

根据式(5)和式(6)(此处2相当于)的计算结果，Ⅰ型三面板单元的膜延展吸能为

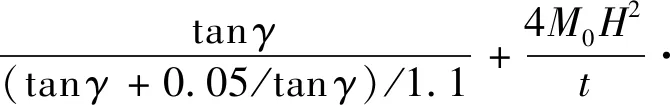
2tan (2)

(7)

与Ⅰ型三面板单元类似，Ⅱ型三面板单元的膜延展吸能同样通过对每个面板的延展区域进行积分得到，图5所示为夹角为的Ⅱ型三面板单元的理想折叠模型，将三面板单元分成1、2、3这3个面板，文献[5]的研究结果表明，1号面板只受弯曲但无拉伸变形，因此其膜能为0，面板2的变形模式与Ⅰ型三面板单元中的附加面板相同；3号面板被拉伸，通过对图5所示的蓝色阴影区域进行积分得到3号面板的膜延展吸能，2号和3号面板膜延展吸能计算式分别为

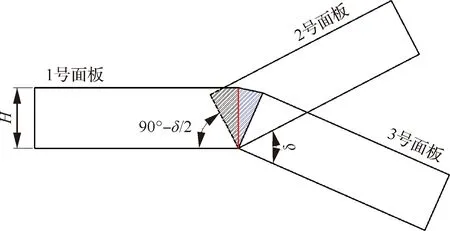
图5 Ⅱ型三面板单元变形过程Fig.5 Deformation process of three-panel angular element Ⅱ

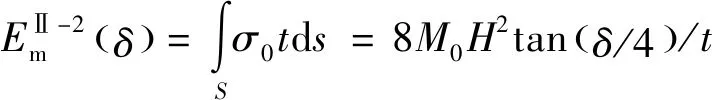
(8)

(9)

除了3个面板的延展吸能之外，Ⅱ型三面板单元变形中还存在面板厚度收缩变形导致的膜延展吸能，该部分计算表达式为

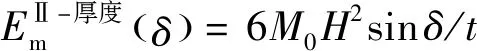
(10)

根据式(8)～式(10)的计算结果，Ⅱ型三面板单元总的膜延展吸能为

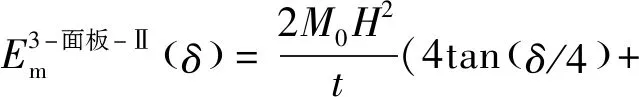
2sin(2)+3sin)

(11)

由图3可以看出，一个夹心八边形代表性单元包括8个=135°的角单元、12个=90°的I型三面板单元和4个=90°的Ⅱ型三面板单元，因此，总的膜延展吸能为

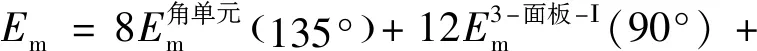
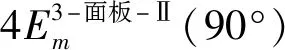
(12)

将式(12)和式(4)代入式(1)，则可得

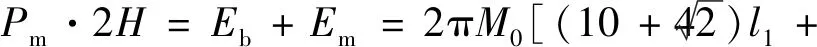
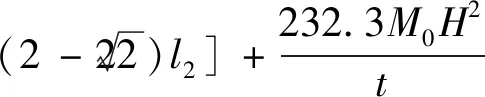
(13)

根据折叠波长使平均载荷取最小值条件有：δδ=0，则

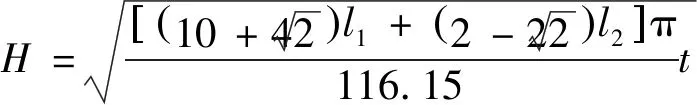
(14)

则夹心八边形蜂窝的平均载荷可以表示为

(15)

考虑到铝蜂窝动态压缩下的惯性效应，引入动态增强系数，对于铝，该系数一般取值范围为1.1～1.6，本文取值为1.2。

为减少同种规格蜂窝因外形尺寸不同对平均载荷的影响，本文以平台应力代替平均载荷来表示夹心八边形铝蜂窝轴向吸能特性，可表示为

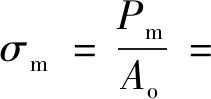
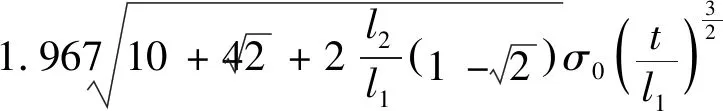
(16)

式中：为夹心八边形胞元的面积。

根据式(16)可以看出，夹心八边形蜂窝的平台应力与壁厚边长比值的3/2次方成正比。

2.2 八边形边长与内嵌四边形边长比对蜂窝相对密度和平台应力的影响

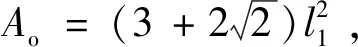
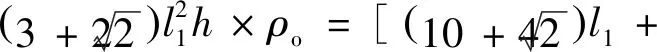
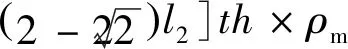
(17)

式中：为蜂窝基体材料的密度。因此夹心八边形蜂窝结构的相对密度为

(18)

由式(16)和式(18)可以看出，蜂窝的相对密度和平台应力是蜂窝壁厚、外部八边形边长以及内部四边形与外部八边形边长比值的函数。当壁厚确定时，并且和的相对比例确定时，模型的整体结构确定。此时相对密度以及平台应力的值主要取决于外部八边形胞元边长。可以看到，随着的增加，相对密度以及平台应力都会降低。

3 夹心八边形蜂窝轴向压缩仿真

3.1 蜂窝轴向压缩仿真方法验证

由于本文新设计的夹心八边形蜂窝结构尚未加工制作，而文献中也没有该类蜂窝结构的试验数据，为了验证本部分建立的夹心八边形蜂窝有限元模型的有效性，本文将通过对常规的六边形蜂窝进行仿真分析和轴向压缩试验，通过仿真与试验的对比以间接验证模型建立和仿真方法的正确性，验证之后，可靠的模型建立和仿真的通用方法可以用于本文设计的夹心八边形蜂窝的轴向压缩仿真和吸能评估。

本试验中所用的蜂窝胞元和样品蜂窝结构如图6所示，其中蜂窝胞元短边长=6 mm，长边长=10.4 mm，夹角=120°，壁厚=0.045 mm，相对密度为0.006。蜂窝试件为长和宽为77 mm、高度为36 mm的长方体试件，统一采用线切割方式进行加工。通过压缩试验机进行试验，设置试验机压头速度为0.36 m/s，对应的应变率为10 s，采集得到力-位移曲线，然后分别根据蜂窝截面尺寸和轴向压缩高度尺寸将力-位移曲线换算为应力-应变曲线。

图6 蜂窝压缩试验细节Fig.6 Details of honeycomb compression test

基于HyperMesh和LS-DYNA建立的轴向压缩铝蜂窝模型如图7所示，根据试验工况，将蜂窝置于两刚性平板之间，下部刚性平板完全固定，模拟支撑平台，上部刚性平板以恒定速度下压。两端刚性板与蜂窝之间设置为自动面-面接触，蜂窝自身设置为自接触。设置铝蜂窝自身接触摩擦系数为0.3，铝蜂窝与刚性隔板之间的摩擦系数为0.1。蜂窝结构采用壳单元进行建模，在壳单元厚度方向设置5个积分点。为了分析网格尺寸对仿真结果的影响，采用1、0.5、0.3、0.2 mm 尺寸的网格进行网格收敛性分析，分析发现网格尺寸对仿真结果有一定的影响，在网格大小为0.3 mm 时，计算结果收敛。综合考虑仿真计算精度和模型计算时间，采用大小为0.3 mm四边形壳单元作为最终网格进行网格划分。

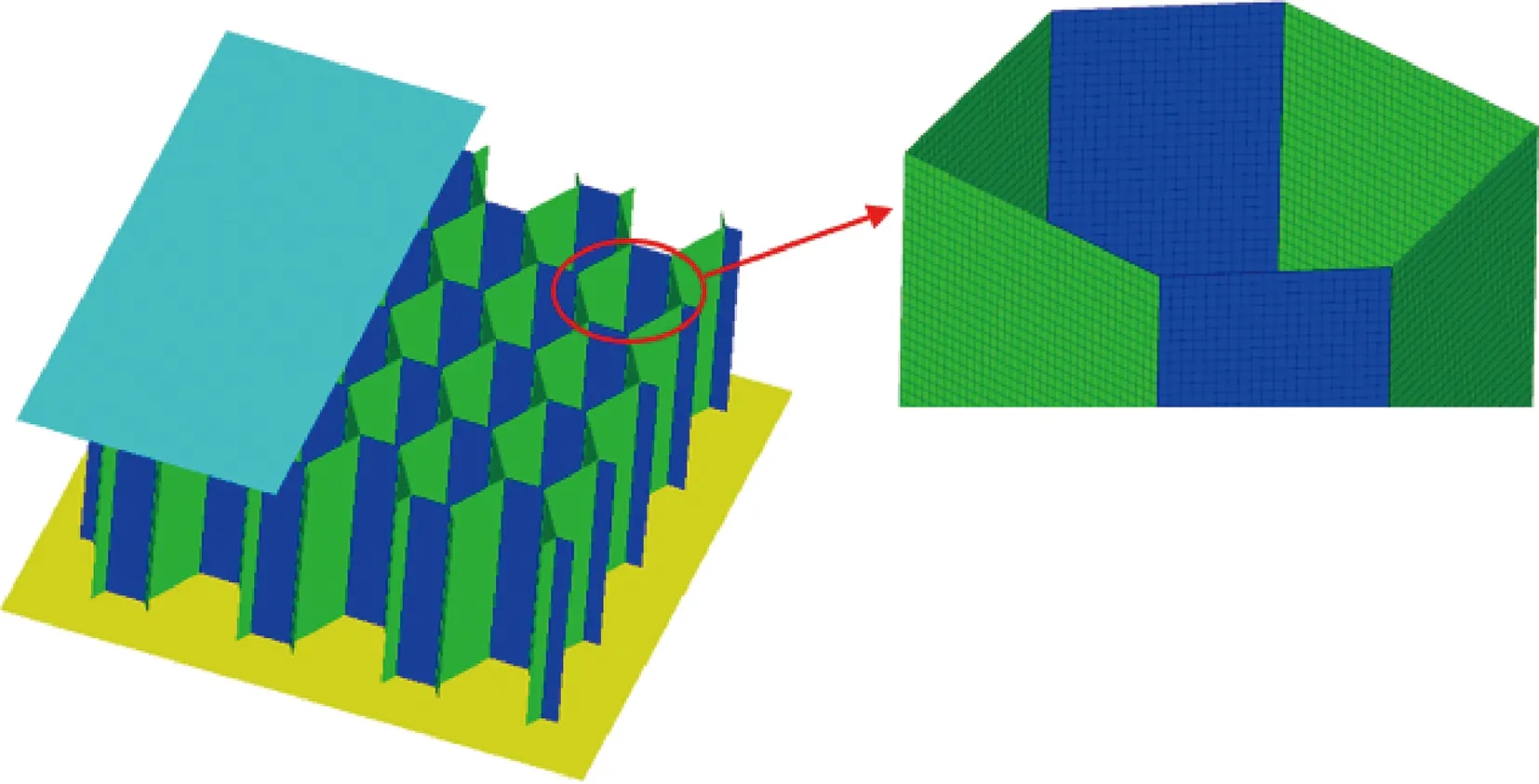
图7 六边形蜂窝有限元模型Fig.7 Finite element model of hexagon honeycomb

蜂窝材料采用多段线性弹塑性模型(MAT24)进行模拟，铝蜂窝材料参数通过对铝蜂窝铝箔基体材料进行试验获得，具体的参数结果如表1所示。

表1 铝蜂窝基体材料参数Table 1 Material parameters of aluminum honeycomb

仿真与试验应力-应变曲线的对比和蜂窝变形过程如图8(a)所示，可以看出，压缩过程中，胞壁向下屈曲，褶皱从加载端开始逐个形成，逐次保持到密实化状态，与试验保持一致。但是可以看到，仿真结果与试验数据吻合较好，初始峰值相等，平台段应力值大小相符。除此之外，为了进一步验证模型，本文使用文献[22]中3003铝蜂窝在10 m/s压缩速度工况下的试验数据进行了仿真验证，建模的蜂窝尺寸和材料参数均与文献[22]保持一致。10 m/s压缩速度工况下的仿真应力应变曲线与文献[22]中给出的平台应力值如图8(b) 所示，仿真平台应力与文献中试验数据仅存在5%的误差，一致性较好，进一步验证了仿真方法的正确性。综合上述两部分的试验验证，说明该仿真模型具有较好的精度，验证了建模和仿真方法的正确性，可以用于下一步夹心八边形蜂窝的仿真和承载吸能评估。

图8 蜂窝压缩应力-应变曲线的仿真和试验结果对比Fig.8 Comparison of honeycomb compressive stress-strain curves between experimental and simulation results

3.2 夹心八边形蜂窝仿真分析及理论模型验证

在仿真模型和建模方法经过准确性验证的基础上，依据3.1节所述建模方法建立夹心八边形蜂窝的轴向压缩仿真模型，如图9所示。

图9 夹心八边形蜂窝有限元模型Fig.9 Finite element model of cored octagon honeycomb

夹心八边形蜂窝轴向压缩变形如图10所示。可以看出，夹心八边形蜂窝轴向压缩的变形模式依然与六边形蜂窝类似，首先位于底部的胞壁首先发生弯曲变形，模型整体向下形成规则的褶皱变形，逐步压溃进入密实段。由于内嵌四边形蜂窝填充了八边形蜂窝的内部空隙，两者中间的肋板通过发生弯曲变形，同时限制了外部八边形蜂窝和内嵌四边形蜂窝竖直胞壁的规则折叠变形，这样就会导致夹心八边形结构的轴向承载力提高，达到了在有限的空间内提升吸能能力的设计目的。

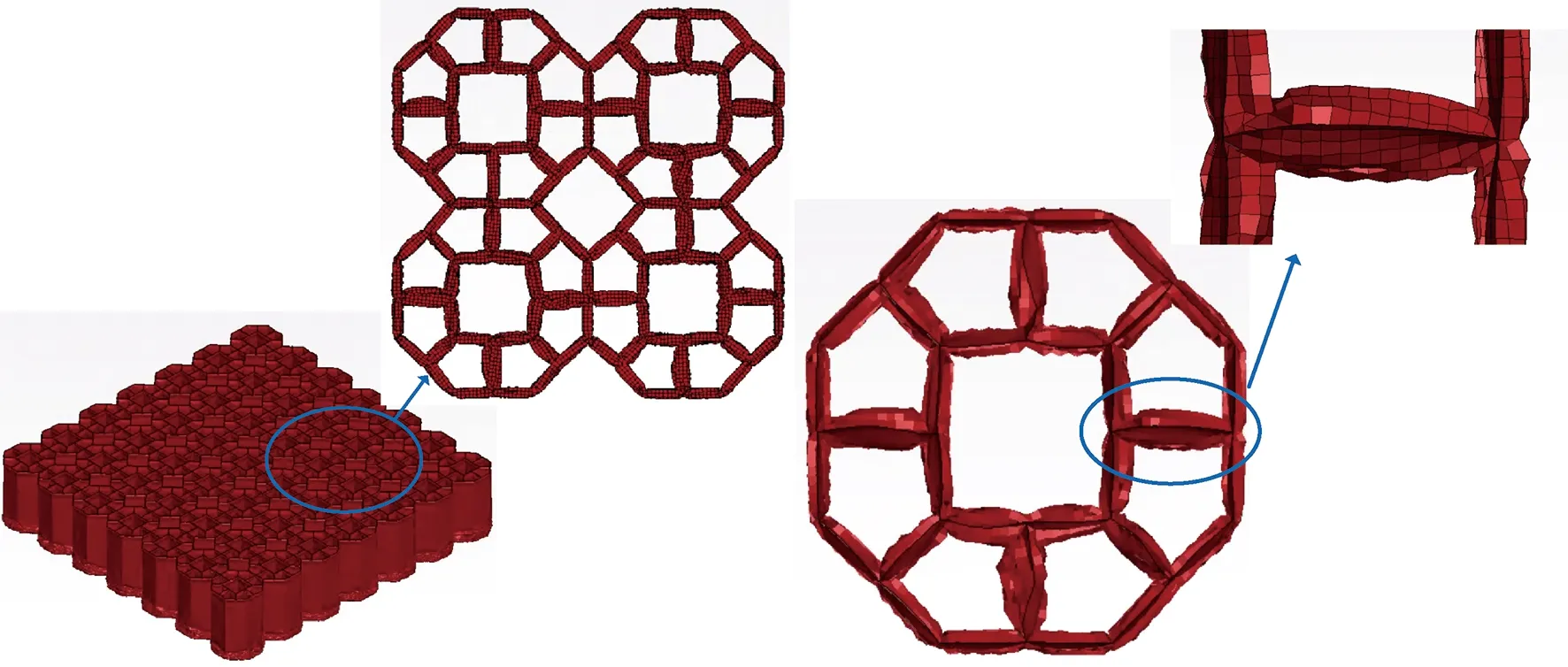
图10 夹心八边形蜂窝变形模式Fig.10 Deformation mode of cored octagon honeycomb

图11 夹心八边形蜂窝平台应力及相对密度随边长的变化趋势Fig.11 Variation trend of platform stress and relative density with side length for cored octagon honeycomb

此外，本文对不同、值以及不同壁厚的夹心八边形蜂窝进行了仿真计算，平台应力以及相对密度的理论模型与仿真结果的对比如表2所示。可以看出，理论公式推导结果与仿真结果误差在5%以内，理论模型具有较高的精度。

表2 理论模型与仿真结果对比Table 2 Comparison of theoretical model and simulation results

3.3 夹心八边形蜂窝与其他典型蜂窝结构吸能能力的对比分析

本节通过比吸能和平台应力两个重要的吸能评估指标来评估夹心八边形蜂窝的吸能能力，其中比吸能(SEA)是评价不同材料或结构在压溃过程中能量吸收能力的重要指标。质量比吸能和体积比吸能的计算表达式为

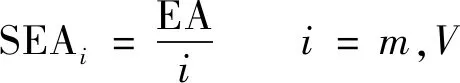
(19)

式中：EA为蜂窝压溃过程中总吸收能量，对于不同的蜂窝结构，不同密实程度的吸收能量不同，本文考虑的总吸能是指蜂窝从初始压缩时刻至蜂窝密实化阶段开始时刻为止；为蜂窝质量；为蜂窝的体积。显然比吸能越大，代表蜂窝吸能能力越好。

平台应力()作为评估蜂窝压溃过程中吸收能量的关键参数，将载荷位移曲线按照2.1节所述转化为应力应变曲线后，计算表达式为

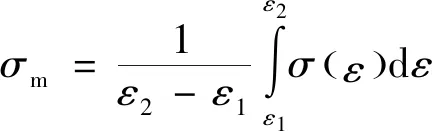
(20)

式中：和分别表示蜂窝轴向承载时平台段的起始和终止应变。

对于不同的蜂窝构型，考虑到不同尺寸参数对承载能力的影响不同，因此本文为横向比较夹心八边形蜂窝的轴向承载能力，引入相同控制条件下的六边形、正方形等常用蜂窝构型。

考虑到蜂窝结构在实际应用时通常会面临安装体积或质量要求更为苛刻的不同情况，出于不同考虑，本文引入了两种不同的控制条件。第一种控制条件下，考虑到蜂窝吸能的重要指标平台应力主要取决于壁厚与边长的比值。因此，首先保证各个构型的壁厚边长比值相等。并且在建模过程中保证蜂窝单个胞元的横截面积相等，蜂窝结构高度均为30 mm，模型所含完整胞元数目一致，此种控制条件可以有效评估不同构型蜂窝在安装空间更为有限的情况下吸能的效果，不同构型蜂窝的尺寸及模型信息如表3所示。

此外为了评估不同构型蜂窝在质量要求更为苛刻的情况下的承载能力，第二种控制条件下保证不同的蜂窝构型相对密度一致。对于不同的蜂窝构型，相对密度与胞孔尺寸间的关系不一致，相对密度不同会导致力学性能存在差异。本文控制不同蜂窝相对密度均为0.02，壁厚为0.03 mm，此时不同构型蜂窝的尺寸及模型信息如表4所示。

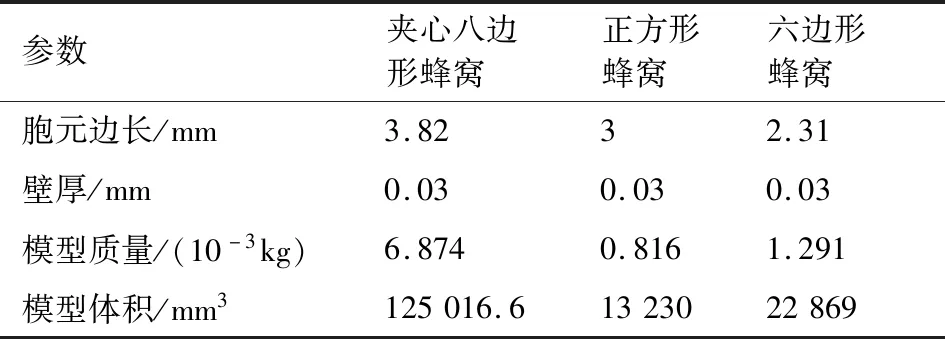
表4 相对密度一致时不同构型蜂窝的尺寸及模型信息Table 4 Geometric information of different honeycombs with same relative density

按照前面所述指标的计算，在上述两种情况下，不同构型蜂窝的质量及体积比吸能和平台应力的结果对比如图12及图13所示。可以看出，在胞元横截面积一致且壁厚与边长比值固定的情况下，新提出的夹心八边形蜂窝均大幅度领先于六边形和正方形蜂窝，体积比吸能和平台应力甚至达到了六边形蜂窝的两倍以上。这就意味着如果实际安装空间有限，对于蜂窝安装体积要求很苛刻的情况下，本文提出的夹心八边形新型蜂窝可以在有限的体积内起到更好的缓冲吸能效果。而在控制相对密度一致时，夹心八边形蜂窝的3个指标均与最常用的六边形蜂窝持平，承受轴向压缩时可以起到较好的吸能效果，且均优于正方形蜂窝。这意味着夹心八边形蜂窝在安装质量要求苛刻的环境下也能表现出较好的缓冲吸能效果。综合来看，本文新提出的夹心八边形蜂窝的轴向压缩吸能优于目前应用广泛的六边形和正方形蜂窝，而且更适合应用在安装体积苛刻的实际使用环境下，是一种吸能效果良好的新构型蜂窝。

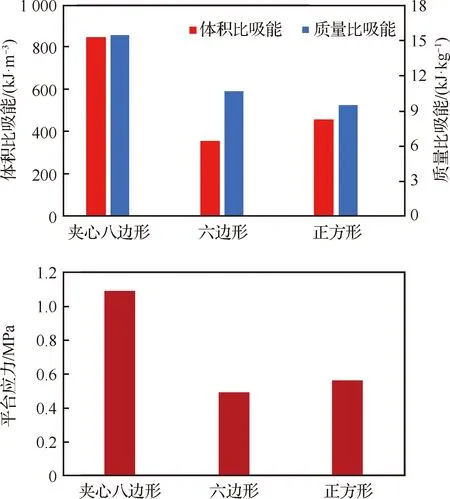
图12 壁厚边长比值相同情况下不同蜂窝承载和吸能对比Fig.12 Comparison of load-carrying and energy absorption ability for different honeycombs with same wall thickness to side length

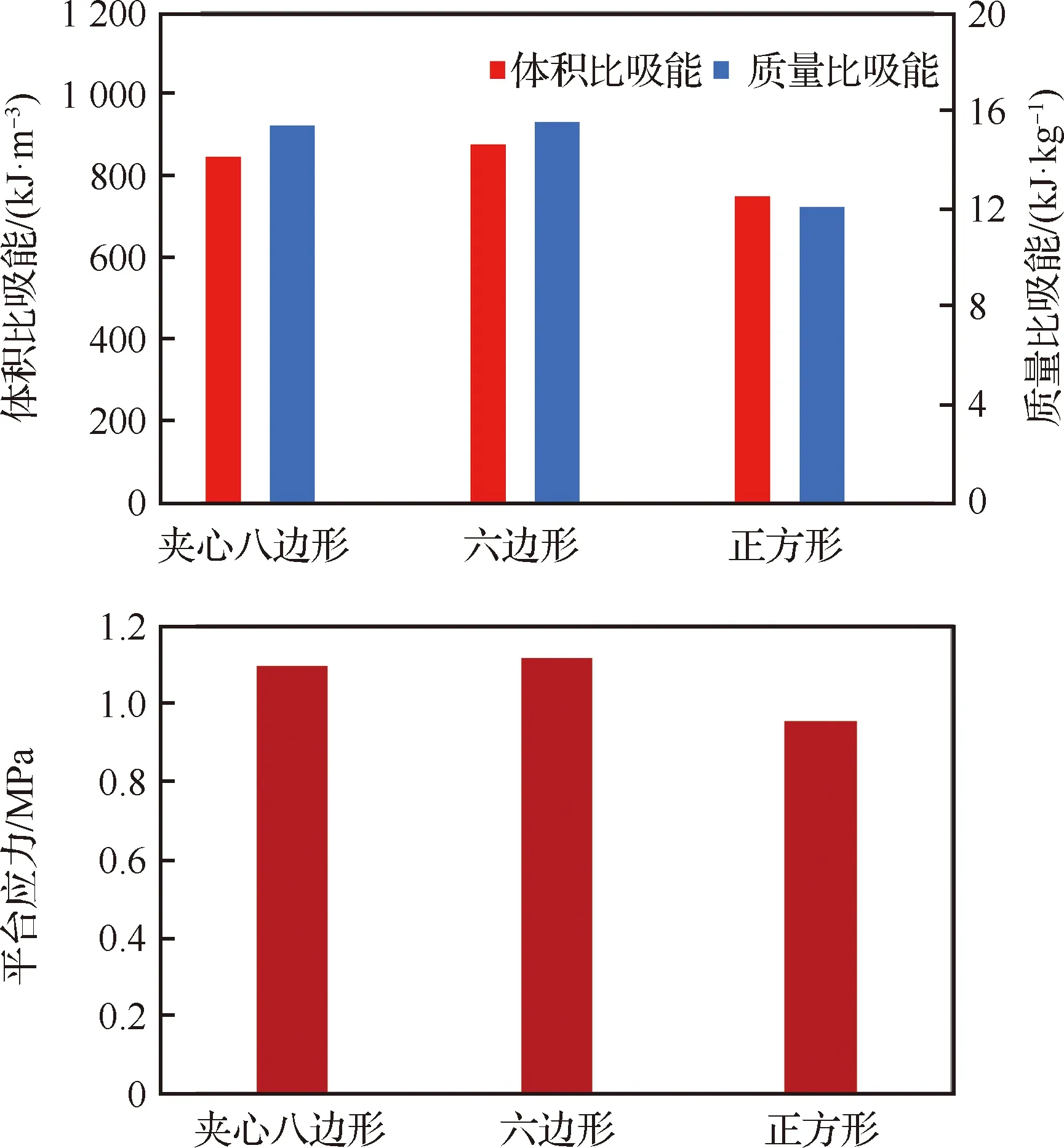
图13 相对密度相同情况下不同蜂窝承载和吸能对比Fig.13 Comparison of load-carrying and energy absorption ability for different honeycombs with same relative density

表3 壁厚边长比值一致时不同构型蜂窝的尺寸及模型信息Table 3 Geometric information of different honeycombs with same ratio of wall thickness to side length

4 夹心八边形蜂窝在直升机驾驶舱抗坠毁设计中的应用

本文以某型号直升机结构为建模依据，建立了简化后的直升机驾驶舱垂向跌落有限元模型来评估夹心八边形蜂窝填充驾驶舱底舱时的吸能效果。该模型由蒙皮、长桁、隔框、底板、横梁、纵梁、支撑板件以及刚性墙组成，有限元模型如图14所示。由于该模型不包括直升机起落架、抗坠毁座椅等直升机坠落时的关键承载结构，因此本节只能在同一条件下定性比较夹心八边形蜂窝相较六边形蜂窝的吸能能力。

图14 直升机驾驶舱有限元模型Fig.14 Finite element model of helicopter cockpit

驾驶舱结构均为铝合金材料，采用MAT24本构进行模拟，统一采用四节点壳单元进行网格划分。整个模型共有429 908个节点，420 785个单元，总质量为2 019.2 kg。为了评估夹心八边形蜂窝的承载能力，在驾驶舱底部的横纵梁交接位置放入等体积的相同壁厚边长比值下的夹心八边形蜂窝或者六边形蜂窝来对比没有蜂窝承载时的情况。考虑到直接采用真实蜂窝模型与驾驶舱模型进行耦合仿真时，两者网格尺寸相差很大导致计算时间过长，因此采用等效实体块建模的方式来建立蜂窝模型。等效蜂窝模型采用MAT126(MAT_MODIFIED_HONEYCOMB)本构进行模拟，将仿真得到的夹心八边形蜂窝以及六边形蜂窝的异面压缩应力应变曲线作为输入，在3个方向上指定相同的非线性弹塑性行为来将蜂窝近似为各向同性模型以评估其在驾驶舱跌落中的承载能力。该本构的杨氏模量从未开始压缩状态到压实状态随体积应变变化而线性变化，具体的材料参数如表5所示。

表5 蜂窝等效模型材料参数汇总Table 5 Summary of honeycomb equivalent model material parameters

该有限元模型各部分的连接关系为:长桁、隔框、底板横纵梁等内部结构采用共节点接触，长桁、隔框、横纵梁等均与外部蒙皮采用MAT100 Spotweld焊点连接。驾驶舱模型整体采用自接触，并且与刚性墙之间采用自动面面接触。底部刚性墙采用完全固定约束，对驾驶舱模型施加大小为10 m/s的初始跌落速度以模拟驾驶舱低空垂向跌落工况。通过机舱底板的最大过载及最大变形量以及碰撞跌落过程中各个承载部件的吸能信息来定性评估夹心八边形蜂窝在直升机驾驶舱低空坠落工况下的吸能效果。

无蜂窝、置入六边形蜂窝、置入新型夹心八边形蜂窝3种情况下的直升机驾驶舱跌落仿真结果分别如图15(a)～图15(c)所示。可以看出，从图15(a)～图15(c)底舱变形量逐渐减小。对于该模型来说，驾驶舱后半部分为驾驶员乘坐位置，该部分为人员保护的关键区域，底板对应的最大变形量及过载结果如图16(a)所示，跌落过程中各个部件的吸能量如图16(b)所示。结果表明无蜂窝缓冲结构时，直升机底舱基本完全压溃，横纵梁作为主承载部件在该过程中通过塑性变形吸收了大量的碰撞动能，底舱最大变形量为219.5 mm，底板的最大过载为88.9(为重力加速度)。在置入蜂窝后，无论是六边形蜂窝还是新型夹心八边形蜂窝，都大大减少了底舱的变形量，底板的最大过载也得到有效的缩小。蜂窝结构在压溃过程中吸收了大部分碰撞动能，驾驶舱原有结构部分的吸能得到降低。这就意味着蜂窝部件的加入大大缓解了驾驶舱原有结构的承载压力，可以降低横纵梁等原有承载结构的设计要求。结果表明，同壁厚边长比值下的六边形蜂窝吸能能力相对较弱，底舱的最大变形量减少至181.4 mm，底板的最大过载减小至66.1。进一步比较六边形和夹心八边形蜂窝的吸能能力，可以看出，等体积下的夹心八边形蜂窝吸能效果更加，吸能量是六边形蜂窝的1.9倍，这与3.3节结论一致。此外，夹心八边形蜂窝的底板最大过载以及最大变形量得到大幅缩小，最大过载仅为54，最大变形量仅有140.3 mm，大大保护了内部乘客的生存空间。可以看出，本文新设计的夹心八边形蜂窝相较目前应用广泛的六边形蜂窝更加适用于直升机底舱耐坠性设计等对吸能要求较高的工况。

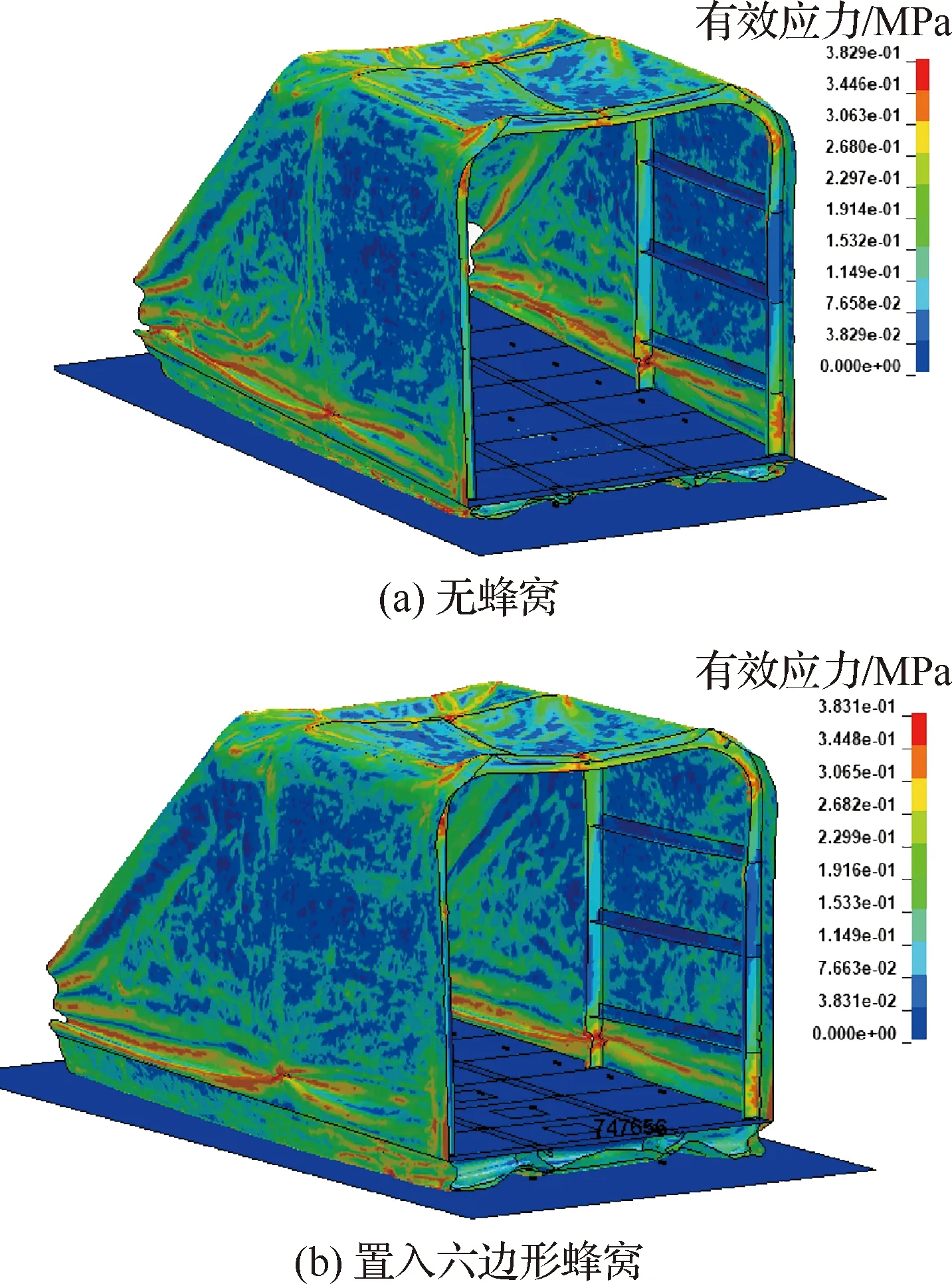
图15 驾驶舱跌落仿真结果Fig.15 Drop simulation results of cockpit

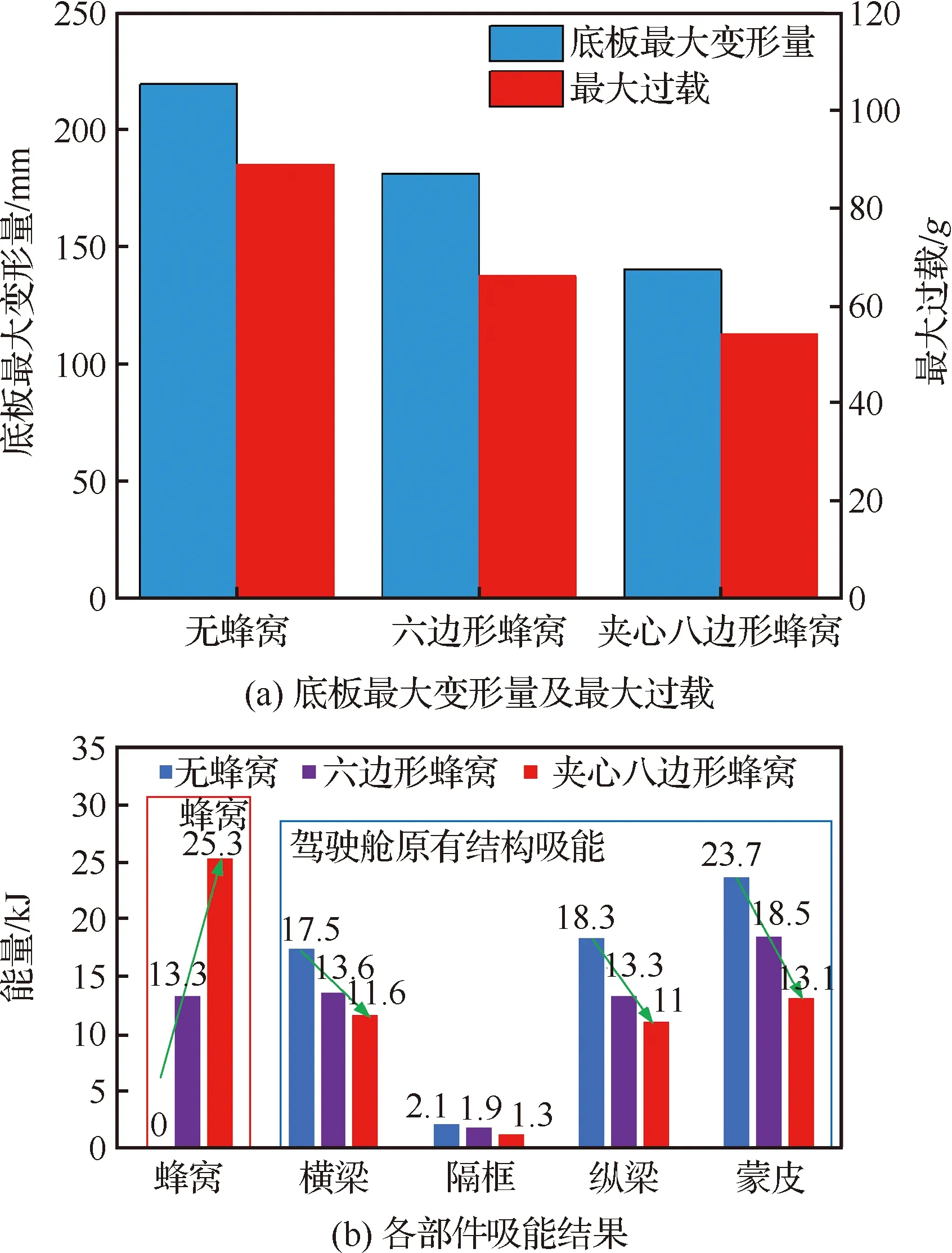
图16 底板变形结果及各部件吸能结果Fig.16 Deformation results of floor and energy absorption results of each component

5 结论及展望

1) 本文提出了一种相较于六边形、正方形蜂窝吸能能力更加优秀的新型夹心八边形蜂窝。首先建立了可快速预测其轴向压缩平台应力的理论模型并进行了尺寸参数对平台应力及相对密度的影响分析。在八边形蜂窝边长确定的前提下，随着四边形蜂窝边长的增加，夹心八边形蜂窝的相对密度降低，轴向承载平台应力逐渐减小；当四边形蜂窝与八边形蜂窝边长比值固定不变时，八边形边长与相对密度成反比，八边形边长的三次方与平台应力成反比，随着八边形边长的增加，相对密度以及平台应力都会有所降低。

2) 通过六边形蜂窝轴向压缩试验和仿真对比，验证了蜂窝建模和仿真方法的正确性；在此基础之上，建立了新型夹心八边形蜂窝的轴向压缩仿真模型，对其变形模式和尺寸参数对能量吸收能力的影响进行了仿真分析，验证了理论模型的正确性。与六边形、正方形蜂窝吸能能力的对比分析结果表明:在保证壁厚边长一致的前提下，夹心八边形蜂窝的平台应力、体积和质量比吸能3个指标均优于六边形及正方形蜂窝，在保证相对密度一致的前提下，夹心八边形蜂窝的3个指标均与六边形蜂窝持平，并且大幅度优于正方形蜂窝。

3) 进行了夹心八边形蜂窝与直升机驾驶舱简化模型的耦合跌落仿真，定性分析了夹心八边形与六边形蜂窝的吸能效果。结果表明夹心八边形蜂窝具有更高的能量吸收能力，更适用于直升机底舱耐坠性设计等对吸能能力要求较高的应用场景，今后将进一步设计完善其制作工艺。