华北地区一次对流激发重力波的卫星观测和数值模拟研究

殷青青，任 璐，田文寿，王 涛，杨景怡，张健恺

（兰州大学大气科学学院，半干旱气候变化教育部重点实验室，甘肃 兰州 730000）

引 言

重力波是一种普遍存在的大气波动，一般在低层大气中被激发并向上传播，从而实现能量和动量在垂直方向上的输送，其可以耦合并连接不同的大气层，对局地甚至全球大气的热力和动力结构产生较大影响［1］，如作为热带平流层风场准2 a 振荡（quasi-biennial oscillation，QBO）、准半年振荡（quasisemiannual oscillation，SAO）的主要驱动力［2］，以及重力波拖曳作用导致的夏季冷中间层顶［3-4］。

大气重力波的激发源主要存在于对流层和低平流层，最重要的激发源包括地形、对流、锋面系统、急流和波流相互作用等［5］。在远离地形和斜压不稳定的地区，对流产生的重力波可以传播到中间层直至低热层，并在破碎过程中将自身动量和能量沉积到背景大气中，对该地区垂直动量输送起着非常重要的作用［6-7］。以往研究表明，对流激发的重力波不仅为QBO 提供约四分之一的纬向驱动强迫［8］，还是夏半球平流层动量拖曳的主要来源［9］。然而，对流驱动重力波的机制较为复杂［5］，故对流性重力波的频率、水平及垂直尺度、相速度等特性具有显著的时空变化特征［10-11］。利用多种手段开展更大探测范围、更高时空分辨率的重力波特征分析研究，可为强对流激发的重力波参数化方案提供更加完善的参考依据。

重力波有多种探测技术，主要包括地基探测（如雷达、无线电探空仪等）和空基探测（如卫星观测）。由于受空间覆盖范围影响，地基探测一般用于探测局地的重力波信息［12-15］。然而，对于大量没有地基观测的地区，只能采用卫星探测手段。由于重力波的垂直波长范围为几千米到十几千米，故对探测仪器的垂直分辨率要求较高。COSMIC（con⁃stellation observing system for meteorology，iono⁃sphere and climate）资料的垂直分辨率为0.1 km，且数据较为可靠［16］，优于绝大部分卫星资料，常用于大范围、较长时间尺度的重力波特征研究［17-19］，但由于扫描次数有限，一些重力波事件难以被捕捉到，较少用于局地的重力波个例分析。此外，卫星、雷达等观测资料存在“观测滤波”效应，即不同观测仪器仅对某一给定波谱范围内重力波信号较为敏感［5，20］，这表明单一观测仪器难以揭示重力波的宽谱特征。中尺度数值模式能够提供高时空分辨率输出结果，在研究波谱分布较广的局地对流性重力波特性上有独特优势［21-24］，但模拟结果通常需要观测资料验证［25］，特别是间歇性较强的对流性重力波源［5］。因此，在保证数值模式模拟的重力波具有一定准确性条件下，其结果可为基于观测资料的区域重力波个例研究提供有效补充。

以往关于对流激发重力波的研究多集中在低纬度地区，特别是沿海热带气旋诱发的平流层重力波［11，26-27］，而中纬度地区夏季深对流发生频率也较高，但中纬度地区深对流激发重力波的模拟多侧重于研究重力波基本参数特征，很少探讨深对流对重力波活动的影响［28-30］。因此，中纬度地区夏季深对流激发的重力波特性及其与对流活动的关系值得进一步研究。2010 年8 月4 日华北地区上空发生了重力波事件，并伴随着较强的深对流活动，AIRS（at⁃mospheric infrared sounder）和COSMIC 同时探测到非常明显的重力波活动。由于华北地区远离高大地形，地势较低，受地形影响较小，探测到的重力波主要由深对流活动激发，这为基于多种资料探究中纬度对流性重力波特征提供了有利条件。因此，本文针对此次个例，利用AIRS 和COSMIC 卫星资料初步分析重力波基本特征，并结合FY-2E 卫星资料和ERA5再分析资料对WRF模式模拟的气象场和对流活动以及重力波基本参数进行检验，在此基础上基于模式输出结果进一步分析重力波的主要特征及其与对流活动之间的关系。

1 数据与方法

1.1 数 据

利用搭载在Aqua卫星上的AIRS探测器诊断深对流系统及其伴随的重力波事件。AIRS 探测器测量3 个 波 段（8.8~15.4 μm、6.2~8.2 μm、3.75~4.58 μm，共2378 个通道）的射出辐射，本文选用8.1 μm（1231.3 cm-1，频段通道号为1291）的220 K亮 温 值 作 为 深 对 流 事 件 阈 值［31］，而4.3 μm（2322.6~2345.9 cm-1和2352.5~2366.9 cm-1，频段通道号对应为2040~2065 和2072~2087）的CO2强吸收带辐射值主要反映平流层的温度变化，采用沿跨轨方向对每条扫描线进行4阶多项式拟合的方法去除背景项和扫描角度的增艳效果，得到的亮温扰动可用于平流层重力波的探测［32-33］。

COSMIC 由美国和中国台湾地区于2006 年4 月合作发射，由6 颗低轨卫星组成，其探测范围广，几乎可以覆盖全球区域，但主要集中在中纬度地区，每天能够获取约2000 个从地表到40 km 高度的大气温度廓线。为了与此次个例发生的时间和空间位置相匹配，选取2010 年8 月4 日105°E—130°E、25°N—45°N 范围内所有数据点，并按照水平距离80~600 km 的标准选取由3 条廓线组成的廓线组（图1）进行重力波信号的提取与分析［19，34］。

图1 WRF模拟区域的海拔高度（填色区，单位：m）和双重网格嵌套区域（矩形区）以及选取的COSMIC卫星廓线位置（红色圆点）分布［红色采样点1（115.60°E，37.04°N）、2（117.36°E，39.83°N）、3（118.08°E，36.56°N）的扫描时间分别为12：19、18：30、12：19（世界时）］Fig.1 The altitude（color shaded areas，Unit：m）of simulation area by WRF model and double grid domains（rectangle areas），and the location distribution of selected profiles from COSMIC satellite（red dots）（The scanning time of red sampling point 1（115.60°E，37.04°N），2（117.36°E，39.83°N）and 3（118.08°E，36.56°N）is 12：19 UTC，18：30 UTC and 12：19 UTC，respectively）

此外，FY-2E 卫星每90 min 可获取一张完整的圆盘影像，覆盖范围为45°E—165°E、60°S—60°N，其红外通道提供的相当黑体亮度温度（black body temperature，TBB）产品具有较高的时空分辨率（时间分辨率为1 h，空间分辨率为5 km×5 km），能够定量指示对流云的发展高度，从而较好地反映强对流天气系统的发生、发展和消亡过程［35］。

1.2 重力波提取方法

参考前人研究［11，36-37］，本文基于卫星温度数据提取重力波扰动的方法如下：在每个纬度带上沿纬圈采用Lomb 最小二乘法拟合0~6波分量，构建大尺度背景温度场，原始温度场减去背景温度场即得到由重力波引起的扰动温度廓线。在对每条廓线进行小波变换时，可通过每个高度功率谱的谱峰确定垂直方向上主导波长及对应的振幅和相位。最后，从背景温度廓线和重力波扰动温度廓线中获得局地浮力频率和重力波势能密度，计算公式［37］如下：

式中：N（z）（s-1）为z高度的浮力频率；Ep（z）（J·kg-1）为z高度的重力波势能密度；g（m·s-2）为重力加速度，忽略其随纬度和高度变化，取常值9.806 65 m·s-2；cp（J·kg-1·K-1）为定压比热，本文取1004.5 J·kg-1·K-1；T0（z）（K）为z高度的背景温度；∂T0(z)∂z（K·m-1）为z高度背景温度梯度；T'（z）（K）为z高度的重力波扰动温度。

另外，重力波的水平波长和动量通量参数则需要综合更多的廓线信息计算获得，本文采用SCHMIDT 等［19］研究方法，适当放宽廓线组空间距离［34］，基于3 个互不共线的掩星测量组（图1）的温度廓线计算重力波的水平波长和动量通量。

1.3 WRF模式模拟

采用中尺度数值预报模式WRF V4.0 版本，选取欧洲中期天气预报中心ERA5 再分析资料（时间分辨率为6 h）作为模式初始场和边界场。模拟区域采用Lambert投影双重网格嵌套，中心位置为117°E、37°N，模拟区域范围和嵌套设置见图1，其中内外层水平分辨率分别为8、24 km，格点数分别为316×280、193×181；垂直方向上分为90 层，12~42 km 高度内采用500 m 等间距，模式顶部气压为1 hPa；模拟时间步长为90 s，每隔30 min 输出一次结果。为避免波动在边界发生反射，在上边界设置了5 km 厚的阻尼层。模式的参数化方案见表1。

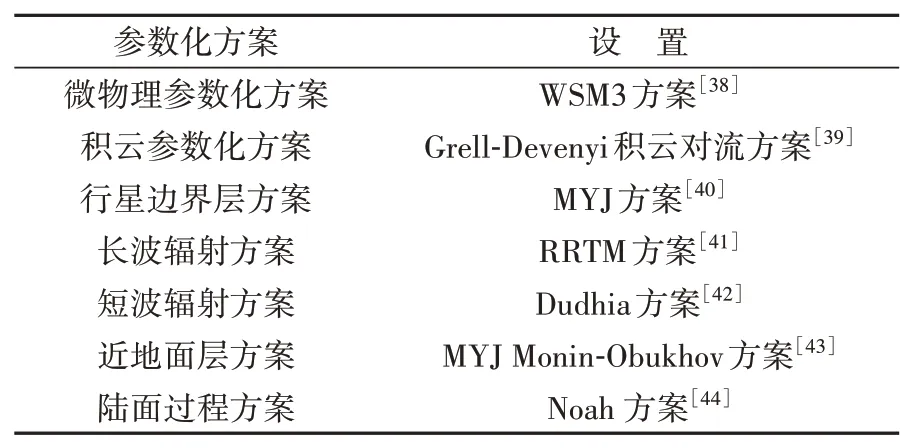
表1 WRF模式的参数化方案设置Tab.1 Parameterized scheme setting of WRF model

将WRF 模式输出的第二重嵌套网格区域模拟的温度、气压和风等物理量分别插值到垂直间隔为500 m 的高度上；然后，对重力波事件发生时段［2010 年8 月3 日18：00 至5 日06：00（世界时，下同）］的温度、水平风在各高度上取平均，并在垂直方向上采用3 阶多项式进行拟合，得到背景温度廓线T0（z）及水平风廓线u0（z）、v0（z）；最后，将模拟的原始廓线减去背景廓线得到温度扰动T'（z）和水平风速扰动u'（z）、v'（z）廓线［45］。

同样，WRF 模式模拟的重力波垂直波长采用功率谱方法得到。参考卞建春等［45］和邓少格等［46］的研究，运用矢量端点连线图分析方法确定重力波的主要频率。根据重力波频散关系，可进一步计算重力波的水平波数、波长及动量的垂直通量。计算公式［45-47］如下：

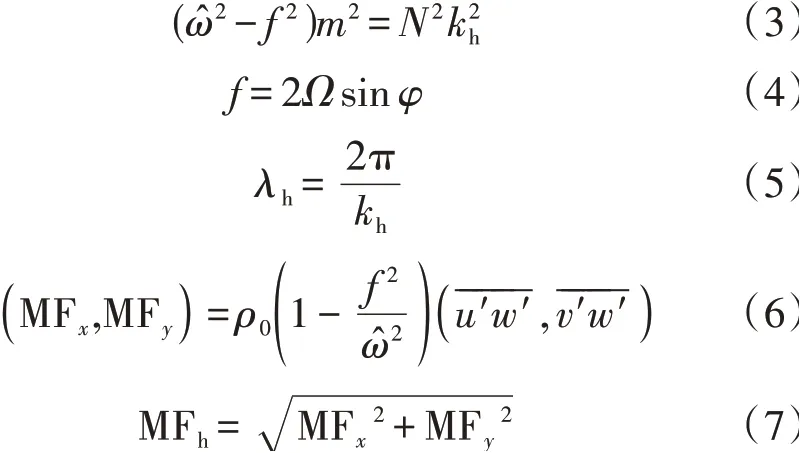
式中：N（s-1）为浮力频率为重力波的固有频率；f（s-1）为科氏参数；Ω（rad·s-1）为地球自转角速度，取7.27×10-5rad·s-1；φ（rad）为纬度；m为垂直波数；kh为水平波数；λh（km）为水平波长；MFh（Pa）为水平动量的总垂直通量（简称“动量通量”）；MFx、MFy分别为动量通量的纬向分量和经向分量；ρ0（kg·m-3）表示背景大气密度；u'、v'、w'（m·s-1）分别表示纬向、经向和垂直方向上的扰动风速。

2 结果与分析

2.1 卫星探测的对流及重力波事件

此次重力波事件主要发生于2010 年8 月4 日06：00—21：00。图2 是2010 年8 月4 日18：05 AIRS卫星观测的8.1 μm 亮温和4.3 μm 亮温扰动振幅分布。可以看出，在110°E—120°E、33°N—38°N 范围内存在亮温值小于220 K 的深对流区域［图2（a）］，且在深对流区东南方110°E—120°E、30°N—37°N范围内亮温扰动（即重力波信号）较为明显，扰动振幅可达0.4 K 以上，重力波大致以该区域为中心呈现较明显的圆弧状分布［图2（b）］，这是对流激发重力波的典型特征［48］。由于AIRS 卫星扫描时该区域对流活动已逐渐减弱消散，故低亮温中心较弱。上述分析可见，通过AIRS卫星亮温可以较为直观地监测到重力波的扰动信号。

为进一步探析重力波特征，利用COSMIC 温度廓线计算3个采样点的重力波特征参数。为避免对流层顶温度随高度剧烈变化对重力波参数计算的影响，选择15 km 以上平流层进行分析。对比采样点1、3，采样点2 扫描时（18：30）对流强度与重力波均有所减弱，对应的扰动温度振幅整体较小［图3（a）］。垂直波长在各高度上变化不大，在7~12 km 之间，平均为9.87 km［图3（b）］，而主导水平波长约499 km（表略）。由此判断，此次事件激发的重力波在平流层以中低频重力波为主。

重力波势能密度和动量通量廓线可分别反映重力波上传过程中携带的能量和动量，由于大气密度随高度呈指数下降，当重力波在上传过程中几乎不发生破碎和耗散时，重力波势能密度随高度近似指数增加，而动量通量则随高度近似保持不变［49］。由图3（c）和图3（d）可见，在15~25 km 高度范围内重力波耗散最快，尤其是采样点1计算的廓线，绝大部分重力波能量和动量聚集在低平流层，25~32 km高度范围内重力波势能密度和动量通量变化不大，而32 km 高度以上采样点3 的重力波势能密度和动量通量明显增大，可能是此高度上波-波相互作用或重力波破碎过程激发出次级重力波［5］，进一步携带能量和动量传送到更高的高度上。可见，COSMIC卫星能够量化重力波的一些主要参数。

2.2 数值模拟结果检验

由于重力波发生区域远离高大地形，卫星资料观测到与重力波信号相伴随的强对流系统，故初步判断此次重力波事件是由强对流活动激发所致。准确模拟重力波激发源，特别是间歇性较强的对流性源，这对于重力波的模拟非常重要。因此，首先需要对模式模拟的气象场进行检验。图4是此次重力波扰动发生期间30 hPa 等压面上WRF 模式模拟的温度场和水平风场与ERA5 再分析资料的对比。可以看出，WRF 模式模拟的温度范围及分布与ERA5 再分析资料比较一致，模式能够模拟出4 日12：00 的温度低值区，但高值区范围略偏大；从风场来看，WRF 模式能够模拟出华北东北部地区的气旋式环流结构，且模拟的环流形态和中心与ERA5 再分析资料较为接近。总体上，WRF 模式模拟的气象场与ERA5再分析资料有较好的一致性。

图4 2010年8月4日00：00—18：00 30 hPa高度上ERA5再分析资料（a、b、c、d）和WRF模式输出（e、f、g、h）的温度场（填色区，单位：K）和水平风场（白色箭头，单位：m·s-1）对比（a、e）00：00，（b、f）06：00，（c、g）12：00，（d、h）18：00Fig.4 The comparison of temperature field（color shaded areas，Unit：K）and horizontal wind field（white arrows，Unit：m·s-1）from ERA5 reanalysis data（a，b，c，d）and WRF simulation（e，f，g，h）at 30 hPa from 00：00 UTC to 18：00 UTC on 4 August 2010（a，e）00：00 UTC，（b，f）06：00 UTC，（c，g）12：00 UTC，（d，h）18：00 UTC

TBB 和云顶温度（cloud top temperature，CTT）都能够反映对流发展的高度和强度（由黑体辐射定律可知，TBB 比CTT 略低），故这2 个量可以反映对流系统的发生发展过程。图5 是此次对流过程中FY-2E 卫星的TBB 和WRF 模式输出的CTT 时间演变对比。可以看出，4 日06：00 对流云团开始发展，对流中心逐渐向东北方向移动，至12：00—15：00发展最为强盛，TBB 最低为190 K，达到深对流系统对应阈值，此后对流云团开始减弱，至21：00仅在辽宁地区分布着较为分散的弱对流体。对比来看，模式输出的CTT 在量值上较卫星观测的TBB 偏小约10 K，但2 种资料展示的对流系统在位置移动、强度变化上都非常接近。

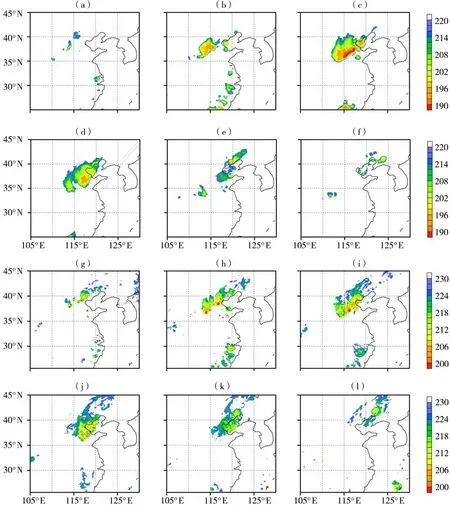
图5 2010年8月4日06：00—21：00 FY-2E卫星探测的TBB（a、b、c、d、e、f）和WRF模式模拟的CTT（g、h、i、j、k、l）对比（单位：K）（a、g）06：00，（b、h）09：00，（c、i）12：00，（d、j）15：00，（e、k）18：00，（f、l）21：00Fig.5 The comparison of observed TBB from FY-2E satellite（a，b，c，d，e，f）with simulated CTT by WRF model（g，h，i，j，k，l）from 06：00 UTC to 21：00 UTC on 4 August 2010（Unit：K）（a，g）06：00 UTC，（b，h）09：00 UTC，（c，i）12：00 UTC，（d，j）15：00 UTC，（e，k）18：00 UTC，（f，l）21：00 UTC

综合对比ERA5 再分析的和FY-2E 卫星观测的平流层气象场及对流活动，发现WRF模式能够较好地模拟出此次事件中真实的大气环境和中尺度对流系统，对流发生发展时段为8 月4 日06：00—21：00，且在最强盛时期达到深对流标准，具备激发重力波条件。

图6是基于WRF 模式结果计算得出的重力波参数垂直廓线。与COSMIC 卫星观测结果相比，整体上WRF模式模拟的重力波扰动温度振幅较大，且相位上略有偏差。WRF 模式模拟的垂直波长和水平波长与COSMIC 卫星观测较为接近。由于COSMIC 卫星采用临边探测技术，仅能探测到水平波长较长的重力波，而当模式分辨率足够高时其几乎可以模拟全波段的重力波，因此WRF模式模拟的重力波振幅、势能密度和动量通量值都大于COSMIC 探测结果，但二者在垂直方向上的分布及变化特征基本相似。上述分析可见，WRF 模式模拟的重力波基本参数与COSMIC 卫星探测结果基本吻合，表明WRF模式能够较好地模拟出这次重力波事件的基本特征，可利用模式输出结果对重力波特征做进一步分析。

图6 2010年8月4日WRF模式模拟的不同采样点扰动温度（a）、垂直波长（b）、势能密度（c）和动量通量（d）廓线Fig.6 The profiles of disturbance temperature（a），vertical wavelength（b），potential energy per unit mass（c）and momentum flux（d）simulated by WRF model at different sampling points on 4 August 2010

2.3 WRF模式输出的重力波特征

为进一步探究此次对流系统触发的重力波信号全局变化特征，对WRF模式输出的30 hPa垂直速度分布进行分析。从图7 看出，8 月4 日06：00 起在112°E—123°E、35°N—43°N 范围内有明显的弧状波结构发展，并随时间不断向四周扩展，强度逐渐增大，于12：00 左右弧状波信号最强、结构完整，大致以117°E、37°N 为中心呈现近似闭合的同心圆状向四周传播，随后强度逐渐减弱，重力波扰动及发展与FY-2E 卫星观测的对流强度演变（图5）基本一致，且扰动中心随对流中心逐渐向东移动。对比AIRS 卫星的亮温扰动分布［图2（b）］，发现二者在112°E—120°E、30°N—37°N 范围内波动信号较为接近。另外，不同时次重力波垂直速度扰动存在差异，但总体上扰动中心偏东方向的垂直速度振幅强于其他水平方向，表明该重力波主要向东传播。

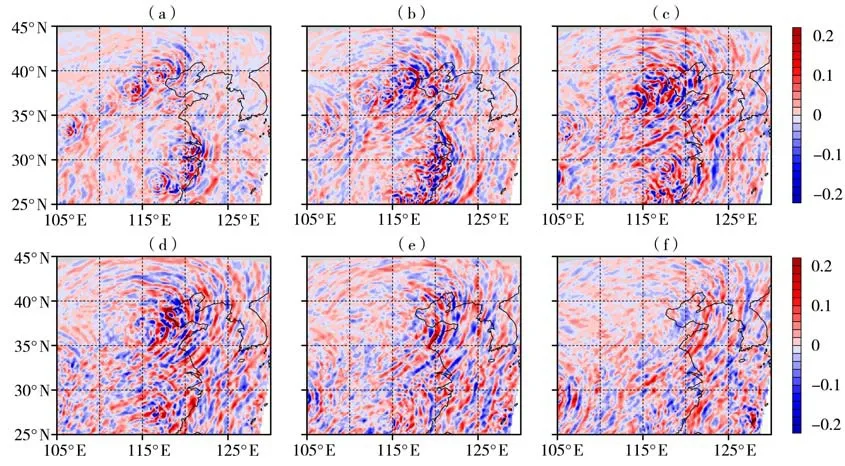
图7 2010年8月4日06：00—21：00 WRF模式输出的30 hPa垂直速度分布（单位：m·s-1）（a）06：00，（b）09：00，（c）12：00，（d）15：00，（e）18：00，（f）21：00Fig.7 The distribution of vertical velocity from WRF model at 30 hPa from 06：00 UTC to 21：00 UT C on 4 August 2010（Unit：m·s-1）（a）06：00 UTC，（b）09：00 UTC，（c）12：00 UTC，（d）15：00 UTC，（e）18：00 UTC，（f）21：00 UTC

为更进一步探讨重力波在垂直方向上的传播特征，对WRF 模式输出的垂直速度和位温沿38°N做高度-经度剖面（图8）。可以看出，4 日12：00，上升运动由地面发展到100 hPa 高度，说明对流发展非常高，并在此高度上激发出重力波信号，向上倾斜传播至42 km 高度未完全破碎。此外，在强重力波信号区等位温线因垂直气流影响发生扭曲，且随高度升高等熵面波动越来越剧烈，从而产生对流不稳定，进而使重力波易发生破碎。18：00 以后，对流层的对流活动强度减弱，对流发展高度有所降低，向上传播的重力波振幅明显减小。

图8 2010年8月4日06：00—21：00 WRF模式输出的垂直速度（填色区，单位：m·s-1）和位温（黑色实线，单位：K）沿38°N的经度-高度分布（a）06：00，（b）09：00，（c）12：00，（d）15：00，（e）18：00，（f）21：00Fig.8 The longitude-height distribution of vertical velocity（color shaded areas，Unit：m·s-1）and potential temperature（black solid lines，Unit：K）from WRF model along 38°N from 06：00 UTC to 21：00 UTC on 4 August 2010（a）06：00 UTC，（b）09：00 UTC，（c）12：00 UTC，（d）15：00 UTC，（e）18：00 UTC，（f）21：00 UTC

基于WRF 模式模拟的气象场，计算整个时段内112°E—125°E、33°N—45°N 范围（重力波信号较明显区域）平均垂直波长、水平波长、势能密度和动量通量随时间和高度变化（图9）。可以看出，这4 个参数随时间都呈先增后减的变化趋势。研究表明，对流重力波的垂直波长和水平波长与对流加热的尺度有关［50-51］，随着对流体发展，潜热加热效应增强，激发的重力波的尺度和能量逐渐增大。此外，这4 个参数在垂直高度上有明显变化，垂直波长最大值出现在上对流层-下平流层（upper tropo⁃sphere and lower stratosphere，UTLS）中，且随高度升高潜热加热变弱，垂直波长逐渐减小，其在平流层中为9~11 km；水平波长在平流层中为650~800 km，极大值出现在低平流层约20 km 高度，该高度上浮力频率达到峰值；势能密度一定程度上代表重力波的振幅，随高度升高大气密度急剧减小，在平流层重力波振幅迅速增大；动量通量大值区主要集中于低平流层，约62%的重力波动量集聚在15~25 km 高度范围内。值得注意的是，在整个重力波事件过程中，平流层势能密度达到峰值的时间较对流最旺盛时刻滞后约6 h，即对流层对流活动在12：00 前后发展最为旺盛（图5），其激发的重力波尺度最大、强度最强，约6 h 后上传至平流层40 km高度。

图9 2010年8月4日00：00至5日00：00 WRF模式输出的重力波垂直波长（a，单位：km）、水平波长（b，单位：km）、势能密度（c，单位：J·kg-1）和动量通量（d，单位：Pa）随高度-时间变化Fig.9 The change of vertical wavelength（a，Unit：km），horizontal wavelength（b，Unit：km），potential energy per unit mass（c，Unit：J·kg-1）and momentum flux（d，Unit：Pa）simulated by WRF model with height and time from 00：00 UTC on 4 to 00：00 UTC on 5 August 2010

图10是不同高度上重力波平均势能密度和对流强度随时间变化。从图10（a）看出，对流活动于4日11：00 发展最为旺盛，而不同高度上重力波平均势能密度达到峰值的时间较对流最强时刻有所延迟，20、25、30、35、40 km高度上分别于14：30、17：00、17：30、18：00、18：30 达到峰值，峰值延迟时间随高度升高逐渐增加。其中，20 km和25 km高度上平均势能密度峰值出现时间相差2.5 h，而后每上升5 km 峰值滞后时间均相差0.5 h，表明在20~25 km高度范围内重力波上传速度较慢，而25 km 高度以上重力波上传迅速。需要注意的是，随着高度升高，重力波势能密度随对流活动增强迅速增大且在对流活动减弱阶段其势能密度下降很快，而在20 km 高度势能密度达到峰值后，随着对流活动减弱其变化较小。由此可见，重力波能量对对流活动强度的响应速度随高度升高逐渐加快。此外，在5 日02：00 以后，40 km 高度的势能密度再次显著增加，而在低层变化则不明显。

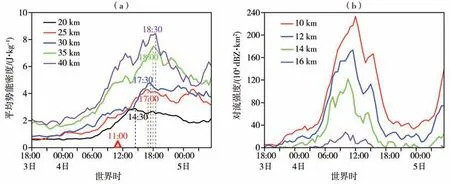
图10 WRF模式输出的不同高度上平均势能密度（a）和对流强度（b）随时间变化（虚线指示不同高度平均势能密度达到峰值的时间，红色三角形对应对流最强时刻）Fig.10 The change of average potential energy per unit mass（a）and convective intensity（b）with time simulated by WRF model at different heights（The dotted lines are the corresponding time with the peak value of average potential energy per unit mass at different heights，and the red triangle marks the moment for strongest convection）

上述分析可见，不同高度上重力波势能密度变化与对流活动变化密切相关。因此，定义雷达反射率因子大于20 dBZ 区域加权求和后的值为对流强度，分析其在各高度上随时间的变化特征（权重为各网格点的面积）。从图10（b）看出，对流活动于4日00：00开始发展，至11：00左右达到最强，并一直发展到16 km高度附近，此后对流活动逐渐减弱，并于5 日02：00开始再次增强，于06：00发展到16 km 高度，因此重力波事件后期40 km 高度的势能密度突然增加与对流再次发展有关。

重力波的传播与背景风场有密切联系，当重力波相速度与背景风相同时，重力波的固有频率无限接近于0，重力波会被背景大气所吸收，该层称为临界层［5］。因此，重力波在水平方向上的传播与背景风同向时，不利于波的上传；反之，当传播方向与背景风相反时，重力波能量衰减较慢，能够迅速上传至较高层。结合图11 可知，当对流发展较浅时，重力波发生高度较低，且在西风中传播的重力波不易上传到更高的高度；相反，当对流迅速发展至16 km高度，突破对流层顶甚至到达零风层时，重力波在东风环境下上传较快，致使高层重力波势能密度迅速增大，当对流减弱后低层的重力波能量持续维持，而高层的重力波能量则迅速减小。因此，5 日02：00，深对流再次发展使得高层的重力波势能密度再次增大。上述分析可见，不同高度上平流层重力波势能密度对对流活动的响应主要与对流的发展高度和背景风场有关。

图11 2010年8月4日02：00至5日06：00 WRF模式输出的u风分量沿38°N的经度-高度剖面（单位：m·s-1）（a）4日02：00，（b）4日06：00，（c）4日10：00，（d）4日14：00，（e）4日18：00，（f）4日22：00，（g）5日02：00，（h）5日06：00（黑色实线的风速为0 m·s-1，紫色实线包围区域的雷达反射率因子大于等于20 dBZ）Fig.11 The longtitude-height section of u component of wind simulated by WRF model along 38°N from 02：00 UTC on 4 to 06：00 UTC on 5 August 2010（a）02：00 UTC 4，（b）06：00 UTC 4，（c）10：00 UTC 4，（d）14：00 UTC 4，（e）18：00 UTC 4，（f）22：00 UTC 4，（g）02：00 UTC 5，（h）06：00 UTC 5（The wind speed for black solid line is equal to 0 m·s-1，and the radar reflectivity factor in area enclosed by purple solid line is greater than or equal to 20 dBZ）

3 结 论

（1）AIRS卫星较好地捕捉到了此次对流活动及其激发的重力波信号，而COSMIC 卫星探测出此次对流系统激发的重力波在平流层以中低频重力波为主，且在低平流层重力波耗散最快。

（2）WRF 模式模拟的重力波激发源及重力波的主要特征参数与卫星观测结果基本一致，在平流层重力波垂直波长主要为9~11 km，水平波长为650~800 km，动量通量主要集中于低平流层，约62%的动量聚集在15~25 km高度范围内。

（3）在此次对流活动发生期间，平流层低层重力波势能密度一直维持较高数值，而上平流层重力波势能密度则在对流减弱后迅速减小，且伴随下一次对流活动再次迅速增加。不同高度上平流层重力波势能密度对对流活动的响应差异主要与对流发展高度和背景风场有关，当对流发展较浅时，其激发的重力波在低层西风中上传的高度较低，易被耗散，而当对流发展较深至16 km 甚至更高时，其激发的重力波接近零风层，并在东风中能够迅速上传。