大骨料混凝土应变局部化中不同粒级粗骨料的作用效应
姜 磊,徐 磊,张菁倪,徐兰玉,任青文
(1.河海大学 水利水电学院,江苏 南京 210098;2.水利部南京水利水文自动化研究所,江苏 南京 210012)
1 研究背景
混凝土是典型的准脆性材料,在损伤开裂阶段呈现出明显的软化特征[1-2],在宏观应力应变曲线上表现为峰值点后,随着应变的增大,应力逐渐减小。在细观尺度上,一般将混凝土视为由粗骨料(粒径大于5 mm)、砂浆以及两者之间的界面过渡区(interfacial transition zone,ITZ)组成的三相复合材料[3]。由于随机分布在砂浆基体中的粗骨料具有不同的粒径、形状、级配和含量,导致混凝土的真实细观(材料)结构极为复杂[4]。混凝土开裂破坏本质上属于多尺度现象,是细观裂纹不断萌生、扩展、集聚和贯通的结果[5-7]。在软化阶段,随着应力的减小,非弹性应变逐渐集中于局部区域,并导致宏观裂缝的产生,这一过程称为应变局部化[8]。应变局部化区域的分布特征与混凝土的细观结构密切相关,并直接影响着混凝土的宏观破坏特性与开裂路径[9]。因此,为在细观尺度上真实模拟混凝土损伤开裂过程,对混凝土细观结构的模拟需达到一定的精度[10-11]。
在以混凝土坝为代表的大体积混凝土结构中,通常采用三级配(小石、中石、大石)或四级配(小石、中石、大石、特大石)等大骨料混凝土[12]。与普通混凝土相比,其粗骨料粒径更大,体积含量更高。三级配、四级配混凝土最大骨料粒径分别为80、150 mm,粗骨料体积含量可达60%~70%,而普通混凝土最大骨料粒径不超过40 mm,粗骨料体积含量一般为40%~50%。此外,为满足统计均匀性的要求,大骨料混凝土细观数值试件所需达到的最小尺寸亦明显大于普通混凝土。上述因素共同导致了在应用以有限元为代表的数值方法开展大骨料混凝土细观分析时计算规模过大[13],致使大骨料混凝土材料与结构多尺度分析受限于细观计算量过大这一瓶颈[14-15]。由于在细观数值模型中模拟数量众多的小粒径粗骨料是导致大骨料混凝土细观计算规模过大的主要原因之一[16],因此,一种缩减细观计算规模的可行方法是简化大骨料混凝土的细观结构,即将部分小粒径粗骨料等效至砂浆基体中。但为真实模拟大骨料混凝土的损伤开裂行为,基于简化细观结构模拟所得的应变局部化区域的主要分布特征应与模拟所有粗骨料的保持一致。为此,有必要揭示不同粒级粗骨料在大骨料混凝土应变局部化中的作用效应,为合理简化大骨料混凝土细观结构提供参考。
为分析某一粒级粗骨料在大骨料混凝土应变局部化中的作用效应,需对比在该粒级粗骨料不同分布条件下(其他粒级粗骨料分布保持不变)应变局部化区域的分布特征。显然,这是采用物理试验手段难以实现的。另一方面,虽然“数值混凝土”已在混凝土计算材料学中得到较为广泛的应用[17-20],但尚未见到将其应用于探究不同粒级粗骨料在大骨料混凝土应变局部化中作用效应的相关报道。本文以四级配大骨料混凝土为研究对象,首先通过建立具有不同细观结构的细观有限元模型并模拟其损伤开裂过程,分析从细观受损至宏观开裂过程中应变与损伤分布特征的演化规律;在此基础上,通过随机改变细观结构中某一粒级粗骨料分布但保持其他粒级粗骨料分布不变的方法,建立一系列用于探究不同粒级粗骨料在应变局部化过程中作用效应的细观有限元模型,并分别开展相应的损伤开裂过程模拟,以探究四级配大骨料混凝土应变局部化中不同粒级粗骨料的作用效应。
2 大骨料混凝土细观有限元模型
2.1 细观结构模拟
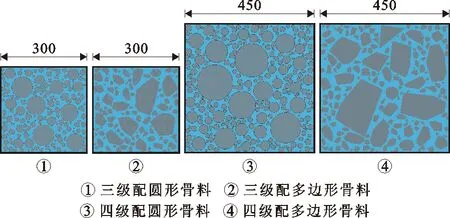
基于先生成随机骨料后进行骨料投放的随机取放法[21],研发了混凝土细观结构随机生成软件AutoGMC。依据给定的混凝土细观结构控制参数(粗骨料的含量及其形状、粒径、级配等),该软件可自动在任意形状模拟区域内完成圆形或多边形骨料细观结构的随机生成。另外,由于混凝土细观结构本质上是三维的,故在生成混凝土试件截面细观结构的过程中,需将混凝土骨料体积含量与级配从三维转换为二维,本文采用Walraven公式[22]实现这一转换,如下式所示:
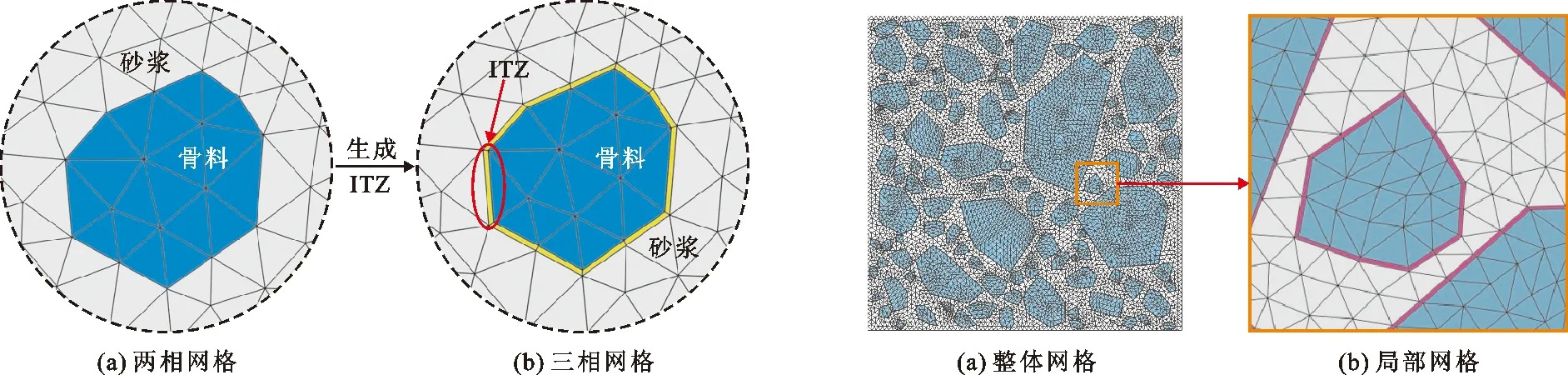
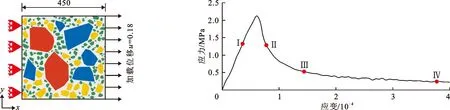
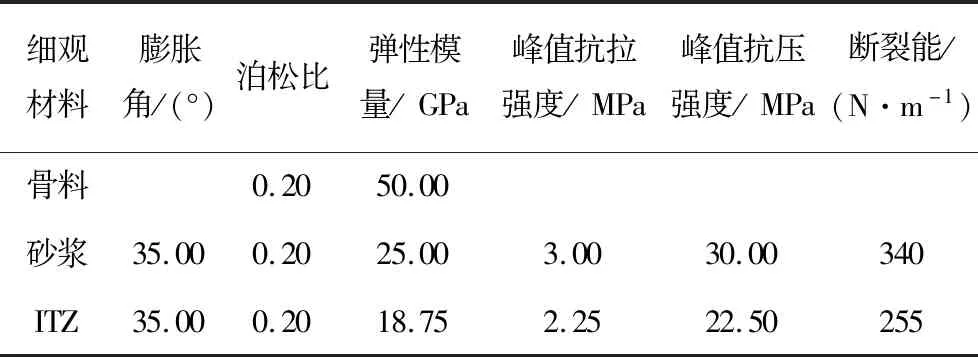
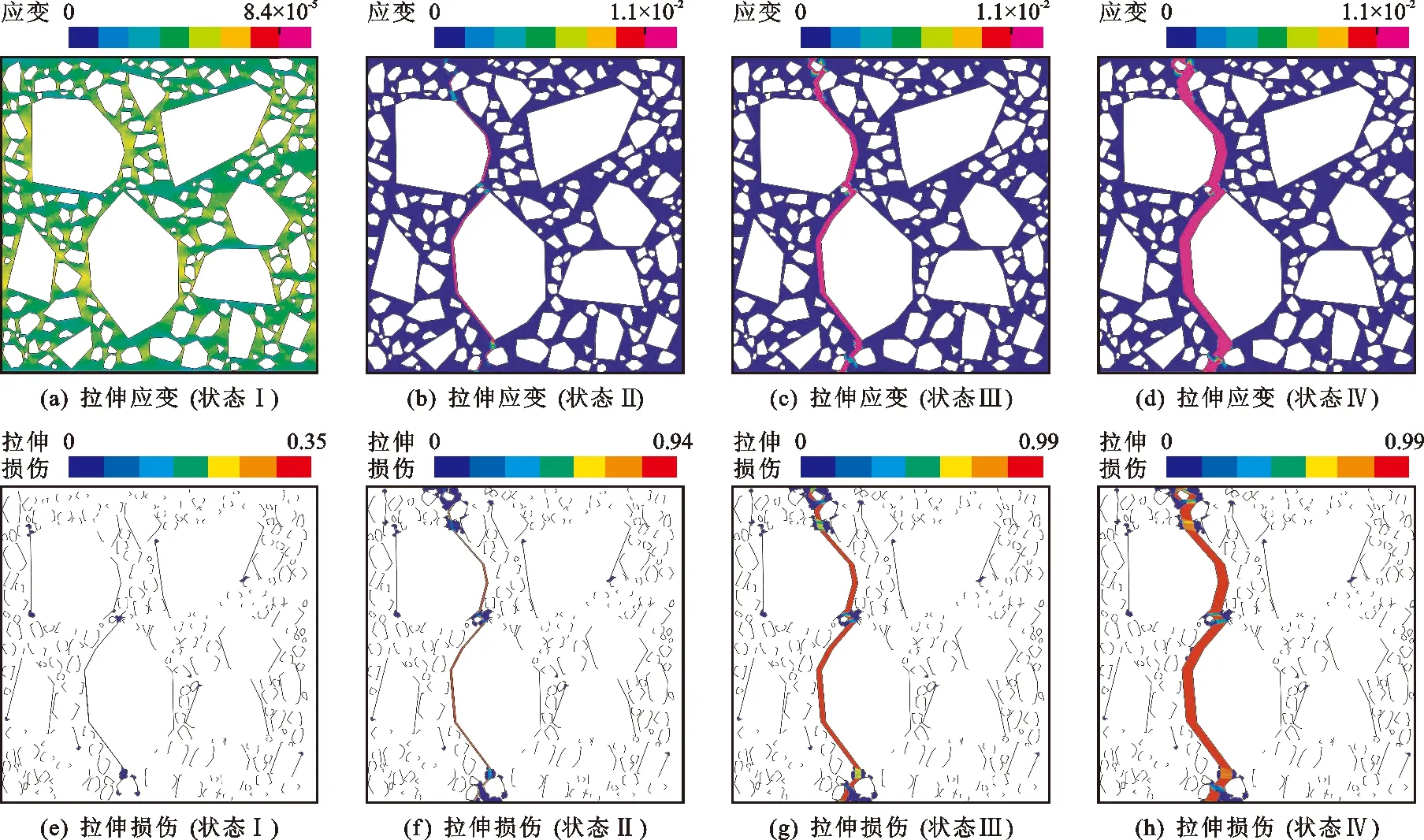
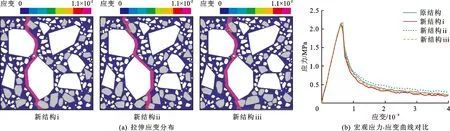
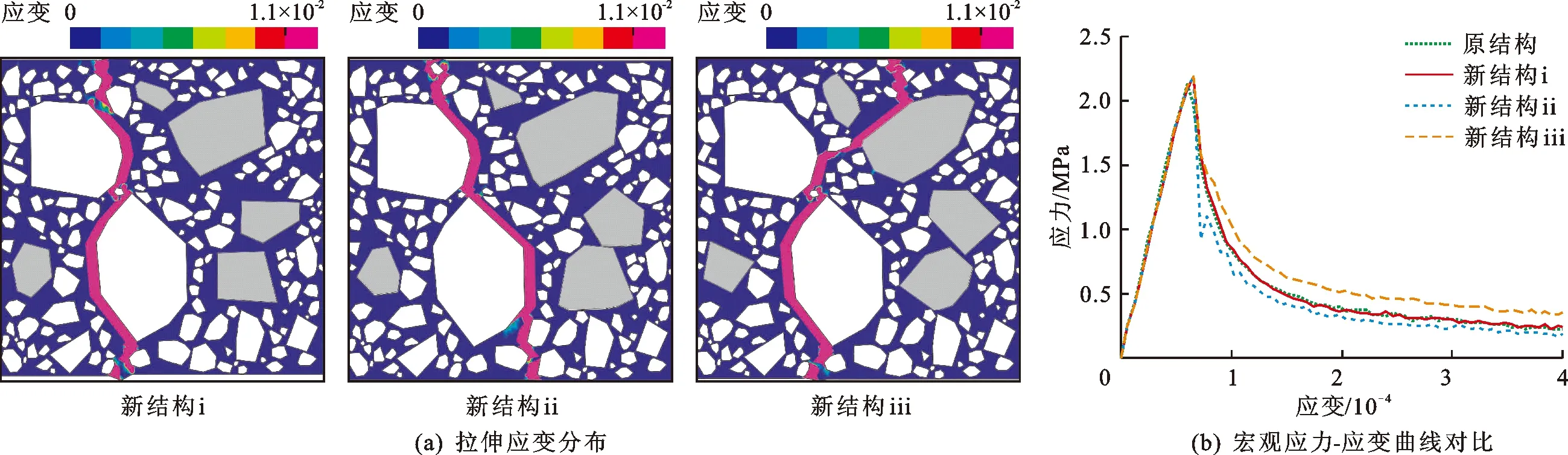
Pc(D 0.053(D0/Dmax)4-0.012(D0/Dmax)6- 0.0045(D0/Dmax)8-0.0025(D0/Dmax)10] (1) 式中:Pc(D 图1给出了三维骨料体积含量为75%的条件下不同级配和骨料形状的大骨料混凝土细观结构生成实例。 为对细观结构进行网格剖分以建立细观有限元模型,利用ABAQUS前处理模块,通过MATLAB和Python混合编程编制了混凝土细观有限元网格自动剖分程序。具体而言,首先基于模拟区域和各骨料的几何信息,依据ABAQUS约定的编写规则[23],自动生成可被ABAQUS前处理模块执行的Python脚本;在此基础上,通过MATLAB调用ABAQUS前处理模块自动完成仅包含骨料与砂浆单元的两相网格剖分;进一步地,为模拟骨料与砂浆之间的界面过渡区,还需收缩前述网格中的骨料边界,以在骨料单元与砂浆单元之间嵌入具有一定厚度(取为100 μm)[24]的界面过渡区(ITZ)单元,从而形成最终的三相网格,如图2所示。采用上述程序完成了图1所示细观结构的有限元网格剖分,见图3。 图1 大骨料混凝细观结构生成实例(单位:mm) 图2 有限元模型界面过渡区单元生成 图3 有限元模型细观网格剖分实例 由于混凝土损伤开裂一般是从ITZ中萌生并向砂浆中扩展,而骨料一般不会发生破坏[25]。因此,本文将骨料视为线弹性材料;采用塑性损伤模型(concrete damaged plasticity,CDP模型)[26]作为砂浆与ITZ的本构模型,体现两者的非线性力学行为[27]。CDP模型应力-应变关系表达式如下: σ=(1-d)D0el:(ε-εpl) (2) 式中:σ为Cauchy应力张量;d为损伤变量;D0el为初始弹性张量;ε为应变张量;εpl为塑性应变张量,其增量(dεpl)表达式如下: (3) (4) 式中:ω为偏心率,用于描述塑性势函数向其渐近线逼近的速度,一般可取为0.1;σt0为单轴抗拉强度,MPa;ψ为膨胀角,(°);J2为有效应力张量偏量的第2不变量;I1为有效应力张量的第1不变量。 CDP模型采用如下形式的屈服函数: (5) (6) 引入拉伸、压缩损伤因子dt、dc分别表征拉伸、压缩损伤导致的刚度退化,其量值分别随拉伸、压缩等效塑性应变的变化而变化。进一步考虑应力反向后的刚度恢复效应,即可给出复杂应力状态下d与dt、dc之间的关系式: d=1-(1-stdc)(1-scdt) (7) 式中:st、sc的取值与应力状态相关[28]。单轴受拉时,st=0,sc=1,故d=dt;单轴受压时,sc=0,st=1,故d=dc。 为分析大骨料混凝土损伤开裂过程中应变与损伤分布特征的演化过程,基于前文第2节所述的混凝土细观结构随机生成软件AutoGMC和细观有限元网格自动剖分方法,生成了3个具有不同细观结构的四级配大骨料混凝土细观有限元数值试件A、B和C,并分别开展了相同条件下的单轴拉伸断裂过程模拟。三维骨料体积含量取为75.00%,相应的二维骨料体积含量为59.87%,骨料级配为特大石∶大石∶中石∶小石= 0.28∶0.28∶0.20∶0.24,细观材料参数见表1。数值试件的细观结构(以试件A为例)、尺寸及加载条件见图4;基于数值试验结果所得的宏观均匀化应力-应变曲线见图5。 图4 四级配大骨料混凝土细观计算模型(单位:mm) 图5 基于数值试验的大骨料混凝土宏观均匀化应力-应变曲线 表1 大骨料混凝土细观材料参数 图6(a)~6(d)给出了试件A中的砂浆和界面过渡区在不同应力状态下(分别对应于图5中的点Ⅰ~Ⅳ)的拉伸应变分布,图6(e)~6(h)为相应的拉伸损伤分布(为便于观察,图中隐去了未受损伤的单元)。图7给出了加载完成后试件B和C中砂浆和界面过渡区的拉伸应变分布及相应的拉伸损伤分布。 图6 不同应力状态下拉伸应变与拉伸损伤分布(试件A) 图7 拉伸应变与拉伸损伤分布(试件B、C) 分析图6可知,在峰前段,虽然在细观尺度上,应变表现出了一定程度的非均匀性,但在宏观尺度上,其分布仍是视为均匀的(图6(a));在峰后软化段,首先在特大石粒级粗骨料与砂浆之间的ITZ处出现了较为明显的应变局部化现象(图6(b)),随着加载位移的增大,应变局部化区域逐渐趋于连通并形成贯穿试件的应变局部化区域(图6(c)),加载位移的进一步增大使得应变局部化区域内的应变集中程度进一步增加(图6(d))。从拉伸损伤方面来看,如图6(e)~6(h)所示,在峰前段,在试件内已出现呈“弥散”分布特征的受损单元(主要为ITZ单元),这与该阶段的应变分布特征一致;在峰后软化段,应变局部化区域的损伤程度不断提高,而试件其他区域损伤状态则保持不变,体现出了损伤演化与应变局部化的直接相关性。 由图6、7可以看出,由于试件A、B、C具有不同的细观结构,故其在受拉过程中,损伤开裂沿不同路径发展,致使应变局部化区域分布存在明显差异;但另一方面,对于不同的细观结构,应变局部化均主要发生在大粒径粗骨料尤其是特大石粒级粗骨料与砂浆间的界面过渡区处,表明大骨料混凝土应变局部化区域的分布主要受到以特大石为代表的大粒径粗骨料在试件内的形状和位置的影响,特大石粒级粗骨料在很大程度上控制着应变局部化区域的主要分布特征。 在上述研究基础上,为进一步分别分析小石、中石和大石粒级粗骨料在应变局部化中的作用效应,以试件A为例,在其细观结构(下称原结构)的基础上,通过随机改变上述某一粒级粗骨料分布(形状和位置)但保持其他3个粒级粗骨料分布不变的方法,形成3种不同的新细观结构并开展与原结构相同条件下的单轴拉伸断裂过程模拟。 图8给出了具有不同小石粒级粗骨料分布的3种新结构条件下的拉伸应变分布及其宏观应力-应变曲线对比。对比图8(a)与图6(d)可以发现,在不同的小石粒级粗骨料分布下,应变局部化区域在试件内的位置基本相同,即小石粒级粗骨料分布的变化并未改变应变局部化区域分布的主要特征,这说明小石粒级粗骨料在应变局部化中的作用很小。由图8(b)可以看出,无论是峰前段还是软化段,包括原结构在内的不同小石粒级粗骨料分布条件下的宏观应力-应变曲线均非常接近,这与上述应变局部化区域分布基本相同的现象吻合。 图8 3种不同小石粒级粗骨料分布下的拉伸应变分布及其宏观应力-应变曲线对比 图9为具有不同中石粒级粗骨料分布的3种新结构条件下的拉伸应变分布及其宏观应力-应变曲线对比。由图9(a)可以看出,中石粒级粗骨料分布改变后,与原结构条件下相比其应变局部化区域分布发生了不同程度的变化,原因不仅在于部分中石粒级粗骨料与砂浆间的界面过渡区直接参与形成贯通的应变局部化区域(图9(a)新结构i),还在于中石粒级粗骨料分布的变化可间接通过对细观应力应变状态的影响改变大粒径粗骨料边界处的应变局部化区域分布(图9(a)新结构ii),表明中石粒级粗骨料在应变局部化区域形成过程中有着较为明显的作用效应。此外,应变局部化区域分布的变化越大,宏观开裂破坏行为的差异就越明显(图9(b)),说明了真实模拟应变局部化区域主要分布特征的重要性。 图9 3种不同中石粒级粗骨料分布下的拉伸应变分布及其宏观应力-应变曲线对比 图10为具有不同大石粒级粗骨料分布的3种新结构条件下的拉伸应变分布及其宏观应力-应变曲线对比。将图10(a)与图6(d)对比可以看出,大石粒级粗骨料分布的变化不仅可通过对细观应力应变状态的影响间接改变应变局部化区域的分布(图10(a) 新结构ii),亦可直接与特大石粒级粗骨料共同控制应变局部化区域的主要分布特征(图10(a) 新结构iii),表明大石粒级粗骨料在应变局部化中的作用效应明显。此外,不同大石粒级粗骨料分布条件下的宏观应力-应变曲线对比(图10(b))再次体现了应变局部化区域主要分布特征与混凝土宏观开裂破坏行为间的直接相关性。 图10 3种不同大石粒级粗骨料分布下的拉伸应变分布及其宏观应力-应变曲线对比 应变局部化区域分布直接影响着混凝土的宏观破坏特性与开裂路径,并与混凝土细观材料结构密切相关。本文以四级配大骨料混凝土为研究对象,探究了不同粒级粗骨料在其损伤开裂应变局部化过程中的作用效应。主要研究结论如下: (1)虽然大骨料混凝土局部化区域分布具有随机性,但主要发生在大粒径粗骨料尤其是特大石粒级粗骨料与砂浆间的界面过渡区处,表明特大石粒级粗骨料在很大程度上控制着应变局部化区域的主要分布特征。 (2)改变大石或中石粒级粗骨料分布均可能导致应变局部化区域主要分布特征的变化,原因在于大石和中石粒级粗骨料可直接或间接在应变局部化区域形成过程中发挥明显作用。 (3)不同小石粒级粗骨料分布条件下的应变局部化区域基本一致,表明小石粒级粗骨料在应变局部化中的作用效应微弱。 (4)应变局部化区域的主要分布特征与混凝土宏观开裂破坏行为直接相关,研究成果可为在建立大骨料混凝土的细观计算模型中合理简化其细观结构提供参考。2.2 有限元网格剖分
2.3 细观力学模型
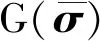
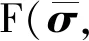
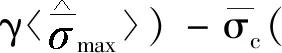
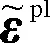
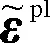
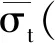
3 大骨料混凝土应变局部化过程分析

4 不同粒级粗骨料的作用效应

5 结 论

