角锥体位置对水流交汇区流场影响的试验研究

王丹薇

（朝阳市阎王鼻子水库工程建设管理局，辽宁 朝阳 122000）

0 引言

我国具有较为丰富的河流资源， 这些遍布全国各地的大小河流在给人们的生活提供便利的同时，也造成了洪涝灾害的高发和频发。 因此，科学、有效的河道治理一直是水力学研究的重点问题。大多数天然河道均具有蜿蜒、 弯曲的平面分布形态，在河流的弯道和交汇部位，水流将出现水面横比降、二次环流等复杂的流动现象[1]。 同时，天然河流的流动都属于紊流状态， 紊流本身是与流体的运动密切相关的，在复杂的水流结构条件下，紊流本身的各向异性将体现出来[2]。 其中，河流的交汇点作为水系连接的关键节点，水流紊动掺混剧烈，且支流的汇入也会对河道主流产生挤压作用，这不仅会在汇入口下游的支流测产生回流涡旋区，还会在另一侧产生流速较大区， 对河床及堤岸产生比较严重的冲刷[3]。 因此，在交汇河道的设置一定的护岸工程，就显得尤为必要。 在护岸工程建设领域，主要有超高法、丁坝以及调整池等。 上述方法各有优劣，往往需要结合使用，优势互补[4]。

为了进一步丰富和优化弯道和交汇部位水流流态改善的工程技术手段， 诸多学者提出了一系列创新性的工程技术手段。 其中，角锥体就是近年来水利工程界提出的改善弯道水流的重要工程技术手段，并取得了良好的工程应用效果。 但是，目前关于将角锥体应用于水流交汇区的研究和实践几乎没有。 在此背景下，此次研究利用室内试验的方式，探讨角锥体对交汇区水流流态的改善作用。

1 研究区域

T 型河道交汇口在实际工程中经常遇到，在这一交汇口处常要解决好以下几个问题：冲刷问题、淤积问题、航行安全问题等，加上水位、水流流向等使这一问题更为复杂。 结合南水北调东线辅助工程泰州引江河配套项目——送水河与南官河交汇口模型试验研究来探讨这一问题。 送水河位于泰州市境内，西端起于高港枢纽，东到合乐村与南官河交汇，交汇角为48°，全长1 860m，它具有引排双向功能（见图1）。在干旱年份，用水高峰期，将高港抽水站调尾，抽引江水100m3/s，经过送水河入南官河，送水到通南高沙腹地，可提高通南地区灌溉标准。 此次研究以上述工程为背景，选择交汇口上游200m，下游100m 为研究区域，利用模型试验的方式探讨丁坝对交汇区流场的实际影响。

2 研究方法

通过在支流汇入岸的对岸侧建立丁坝的方式， 一方面利用丁坝回流区内流速较小可以对堤岸起到一定保护作用， 另一方面利用丁坝的挑流作用对水流交汇区的水流结构加以改善， 具有一定的创新性， 同时还可以为工程实际提供一定的理论依据。

2.1 方案设计

此次研究在主流和支流的来流条件以及角锥体尺寸不变的情况下进行， 主要通过改变角锥体的设置位置，研究其对交汇处水流流态的影响。

基于上述思路， 确定角锥体和交汇断面之间的距离L 作为确定角锥体位置的主要变量。 结合模型尺寸以及角锥体对弯道水流影响的相关研究成果，确定L 的4 个不同取值，分别为0cm、30cm、60cm 和90cm，同时将不设置角锥体的方案作为对比方案。 具体的试验工况设计如表1 所示。

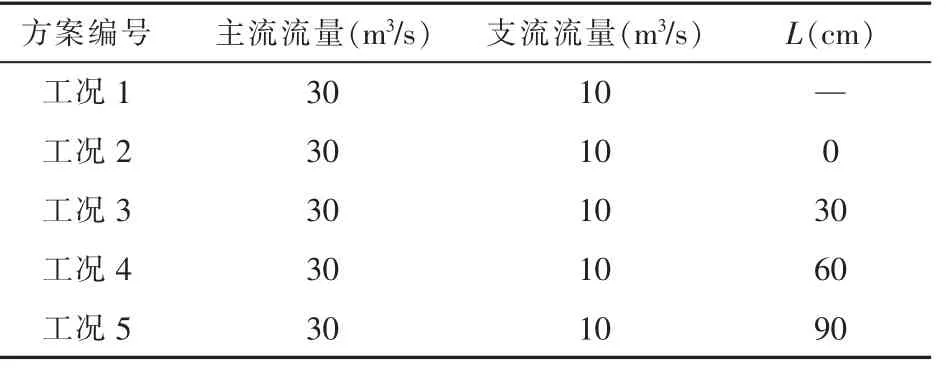
表1 试验工况设计表

2.2 试验模型

此次研究以上述工程背景参考， 按照几何比尺1:100 进行试验模型设计。试验模型主要由水循环系统、 流量调控系统、 测量仪器和其他设备构成。 其中，交汇水槽为概化模型，主槽和支槽的交汇角为90°，其中主槽长6m、宽0.6m，支槽长2m、宽0.2m，高度均为0.3m。 角锥体为三棱锥体结构，其四个面中有两个面临空，一个面与河岸贴合，其临空面又包括与上游来流方向呈一定夹角的面，以及一个下游端面，结合试验水槽的尺寸，其长度设定为10cm，高度为5cm。水槽模型的平面布置示意图如图1 所示。

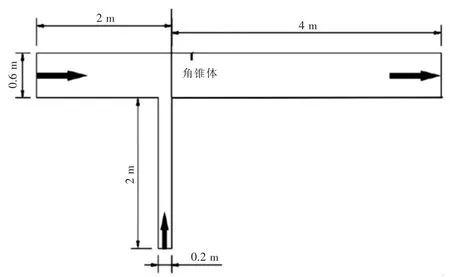
图1 水槽布置平面图

模型采用有机玻璃制作， 在主槽和支槽的入口部位分别设置一道栏栅， 防止污染物对水流的干扰[6]。 模型的采用循环式供水系统，主要包括水箱和水泵两大部件。 其中，水泵为额定流量30m3/h的潜水泵； 水箱为1.5m×0.8m×0.5m 的矩形水箱，其中设有隔板和流量调节板， 可以实现流量的调节，使水流能够按照设定的流量平稳进入水槽。

水流在运动过程中主要受到重力和粘滞力的影响，鉴于水槽水流的雷诺数（一种可用来表征流体流动情况的无量纲数。 Re=ρvd/μ，其中v、ρ、μ 分别为流体的流速、 密度与黏性系数，d 为特征长度。 ）明显大于临界雷诺数，因此重力对水流的影响明显大于粘滞力的影响。 基于此，此次研究中遵循重力相似性原则建立试验水槽[5]。 一般来说，河道的底坡坡降并不大， 此次研究中的底坡选择为0.000 5。

2.3 测试方法

由于三角形堰具有比矩形堰更高的测量精度，同时本次试验的流量相对较小，因此采用三角形薄壁堰进行试验中的流量测定[7]。 其使用的流量公式如下：

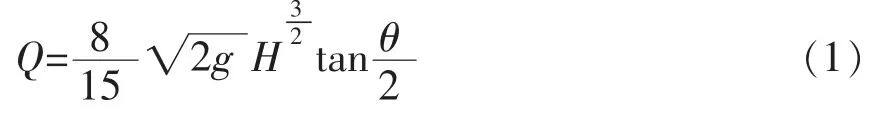
式中，Q 为流量，m3/s；H 为堰上水头，m；θ 为三角堰的角度，°；g 为重力加速度，m/s2。

试验过程中的水深和水面线利用钢尺进行测量，每个测点测量5 次，以5 次测量数据的均值作为该测点的水深数据的最终试验结果。 试验中设置3 个测量断面，测量断面与主槽水流方向平行，与交汇口另一侧的距离分别为10cm、30cm 和50cm，分别观测角锥体部位，水槽中线和汇入口同侧回旋区的水流流态和参数。

2.4 仪器与设备

试验中的流速测量主要采用ADV 超声流速仪，该仪器主要由测量探头，信号调理和信号处理模块构成， 可以兼测二维和三维流速， 其测量范围为0.001—4.5m/s。 在试验过程中，为了减小测量误差，探头需要保持和测绳垂直； 该仪器生成的数据文件为文本文件，便于后续利用Excel 进行数据处理[8]。

3 试验结果与分析

3.1 流速分布

根据相关研究文献，在明渠交汇流中0.6 倍水深部位的流速和垂线平均流速基本相等。 因此，在试验中提取该部位与交汇口另一侧的距离分别为10cm 处的流速试验数据， 绘制出如图2 所示的流速分布曲线。 由图2 可以看出，在没有设置角锥体的条件下， 支流的汇入会使异侧流速值明显增大，在50cm 部位达到最大值，为0.37m/s 左右，最后呈现出逐渐减小并趋于平稳的变化态势。在布置角锥体的各个方案下，流速的最大值明显偏小，说明布置角锥体对控制流速具有明显的作用。 同时，在布置角锥体之后， 水流交汇区的流速变化更为复杂，角锥体前后的流速明显下降。从不同方案的对比来看， 工况3 的流速降幅最大， 其流速的最大值为0.22m/s。由此可见，从保护河床和堤岸的角度来看，工况3 的位置设置可以发挥出最佳的保护效果。

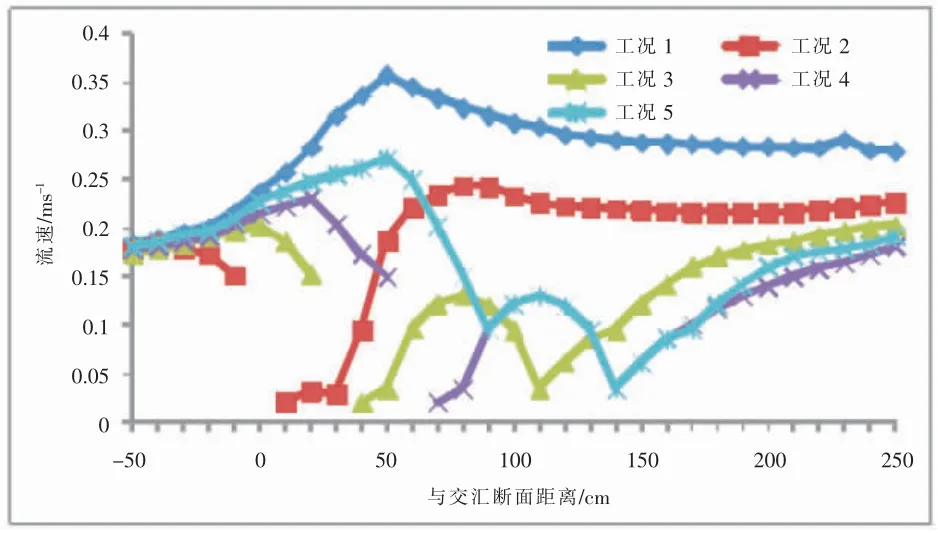
图2 典型断面流速分布曲线

3.2 分离区和坝后回流区特征

支流汇入主流之后， 会在交汇口的下游产生分离区，其内部的紊动作用较为剧烈，流速相对较低。 在对岸设置角锥体之后，会在角锥体后形成回流区，回流区内的水流流速相对较小，可以起到一定的堤岸保护作用[9]。 因此，研究分离区和回流区的几何特征，具有重要的理论意义和现实意义。

根据试验中测量的数据， 总结出不同工况下分离区和回流区的几何特征，结果如表2 所示。 由表2 可知，除了工况2 外，其余角锥体设置工况的分离区长度和宽度与没有设置角锥体的工况1 相比均有明显减小。 由此可见，设置角锥体可以有效减小分离区的长度和宽度。 由于分离区长度和宽度的减小，分离区的面积大为缩小，这对于改善交汇处的水流流态具有重要作用。 从不同设置位置方案的对比来看，工况3 的回流区面积最小，效果最佳。 从回流区的测量数据来看，也呈现出相同的变化规律，随着角锥体与交汇断面距离的增加，回流区的面积呈现出先增加后减小的变化特点，工况3 的回流区范围最大， 可以取得对河床和堤岸的最佳防护效果。

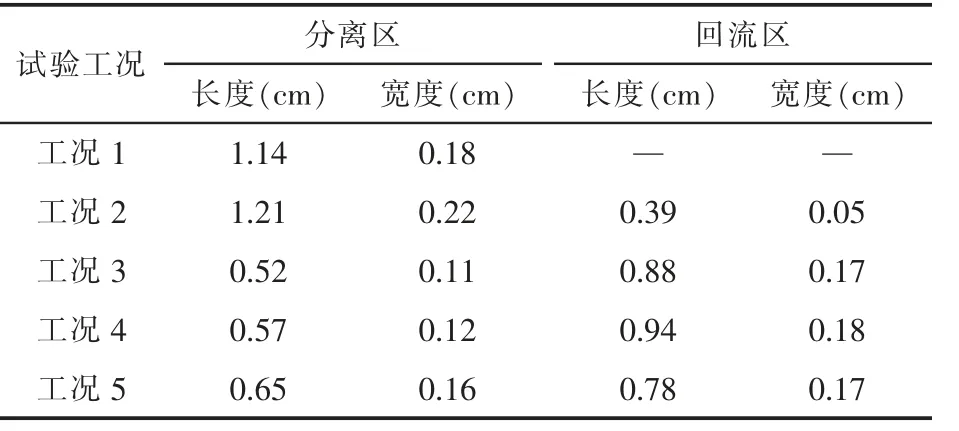
表2 分离区和回流区几何特征

3.3 紊流耗散率

紊流在空间上存在随机涨落， 从而形成比较显著的速度梯度， 并在分子粘滞力的作用下通过内摩擦不断将紊流动能转化为分子运动的动能，从而达到降低流速、改善流态的重要作用[10]。

研究中基于试验数据， 对不同试验方案下的紊流耗散率进行计算， 从计算结果中提取其最大值和存在的部位，结果如表3 所示。 由表3 可以看出，在所有5 种计算工况下，紊流耗散率的最大值均出现为交汇口下游分离区的外侧， 说明该部位存在较强的水流稳定作用。 由于汇入水流和主流在此部位的紊动作用比较强烈， 紊流耗散率也相对较大。 从不同试验工况的结果对比来看，设置角锥体的4 种方案的紊流耗散率明显偏大， 说明设置角锥体具有显著的工程价值。 同时，紊流耗散率最大的是方案3，说明该方案为最优方案。

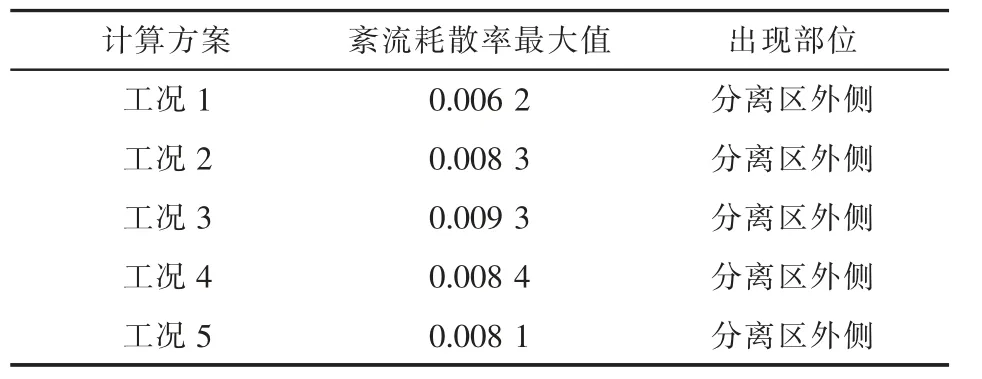
表3 紊流耗散率计算结果

4 结语

此次研究通过室内模型试验的方法， 探讨了在交汇水流条件下角锥体的设置部位对交汇区流场的具体影响。 从实验结果来看，设置角锥体可以起到良好的交汇区流场改善作用， 说明其具有重要的理论意义和工程应用价值。 同时，此次研究获得了角锥体的最佳布置位置， 对其在实际工程中的应用具有一定的指导意义。 当然，此次研究受制于时间和成本等诸多因素的制约， 并没有对角锥体的几何尺寸及设置数量的影响开展进一步的研究， 这也是今后研究的主要方向及应该解决的主要问题。 通过上述两方面的研究，可以获得最佳设置方案，为工程应用提供更有力的支持和借鉴。 □