基于车-路耦合的沉管隧道车辆动力荷载建模与分析

王颖轶, 宋神友, 刘健，黄醒春

（1.上海交通大学，上海 200030；2.深中通道管理中心，广东 中山 528400）

0 引言

车辆与路面的耦合振动直接影响到乘坐舒适性及路面路基的耐久性和安全性，长期以来人们结合工程建设和环境控制的需要，在车辆-路面作用特点、力学模型、计算方法等进行了大量研究且取得了许多有价值的成果。研究的焦点集中于车辆与道路结构的耦合作用与多体系动力建模[1]～[3]、通过线性Hertzian接触模型和快速Fourier 逆变换（IFFT）等耦合作用动力问题的优化求解方法[4]～[5]、基于车辆和道路结构特点的子结构化耦合建模的模态叠加或时程分析方法[6]～[8]、将车辆、路面、路基结构作为一个整体系统建模利用快速傅立叶变换（FFT）方法求解多结构耦合动力问题[9]。但迄今的研究将车辆与路面的处理为连续接触关系，无法反映车辆行驶过程中客观存在的瞬时脱离特性，计算结果难以体现车辆对路面的瞬态冲击作用、低估结构稳定性和耐久性风险。尤其，沉管隧道内车辆与路面的耦合振动问题，至今还少有系统性研究和成果应用，国内现行的设计方法中，对动力作用和超载因素影响的考虑还限于在静力分析基础上加以经验修正，隧道内车辆动力荷载建模及求解相关研究的不足，一定程度影响了沉管隧道服役期安全及寿命评价的科学性和准确性。

该研究在充分考虑沉管隧道结构和车辆结构特性以及路面不平顺激励下的车辆与路面随机脱离现象，建立符合工程特点的车辆—路面耦合动力系统模型及其动力荷载理论解；采用与车辆等速移动的动态坐标系，通过接触力、连接刚度控制选用差异坐标系，并局部修正刚度矩阵和力矩阵；从而实现车-路随机脱离问题的求解。建立了沉管隧道车-路耦合状态下车辆动力荷载计算数学模型和理论解。

1 隧道—车辆动力特性及建模

1.1 沉管隧道公路路面、路基结构

对沉管隧道而言，轮下结构包含面层、基层、隧道结构、隧道下部基础、地基土等。考虑到沉管隧道结构的整体性及隧下基础结构的力学性能，道路结构简化如图1所示。

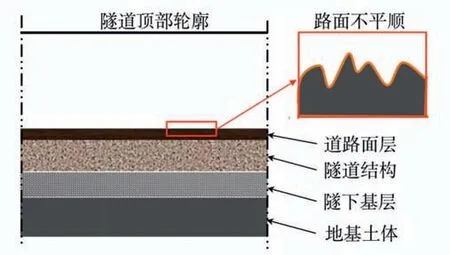
图1 公路隧道的道路结构

路面、路基是公路的主要结构物，它们不仅要求道路能全天候通行，而且要求车辆能以一定的速度，安全、舒适且经济地在道路上行驶。

路面作为高速公路的重要组成部分，其整体及各组成部分必须有足够的强度以抵抗行车作用在路面结构内产生的压应力、拉应力和剪应力。同时，路面也应具有足够的刚度，即路面抵抗变形的能力，使路面各组成部分的变形控制在最小的范围内。否则过量的变形会构成车辙、沉陷、波浪等破坏。一般要求高速公路上形成的累积变形不超过10cm。而且，路面要有足够的平整度，汽车在不平整的路面上行驶时，车轮对路面会产生一个附加的动荷载，它对路面的使用性能和寿命有很大的影响。路基主要对压实度的要求比较高。

如图1所示，尽管现代先进的路面平整施工设备和技术能很好地实现满足设计规范要求的路面平整度，但路面不平顺客观上是无法避免的。同时，随着隧道运营时间增加，随机车辆荷载的作用会使路面形成塑性变形甚至结构损伤、破裂，形成路面不平顺。

1.2 车-路耦合振动系统模型简化

根据车辆的结构特征，将车辆自上而下划分为粘弹性连接的3个刚体动力学结构部件：车体、转向架、车轮。三部分分别由粘弹性连接，形成动力学体系。各刚体之间通过粘弹性结构元件连接（粘弹性参数一般需要进行车辆分类的试验测定）形成三维粘弹性体耦合振动体系。同时，根据以往的研究成果，车轮与路面的接触关系可等效简化为弹性接触，一方面简化了计算，同时也可根据需要研究车轮与路面的瞬间跳离模拟问题。

模型的耦合条件等效处理为：（1）车轮与路面接触点处位移相等；（2）车路与路面接触点互为作用力与反作用力；（3）路面与路基的交界面上的结点编号相同，位移相等。

综上所述，车辆主要由车体、转向架及轮对组成。隧道内高速公路简化为道路面层、基层和隧道结构层。车-路耦合动力系统的轴向连接关系如图2所示。

图2（a）所示的结构模型中，仅考虑了车辆前后轮对的竖向连接关系。对于不同的车辆，可通过该模型的叠加方法建立，比如对于重型超长车辆，多组轮对可通过直接沿隧道轴向叠加组合形成单车车辆体系。车-路耦合动力系统的横向连接关系如图2（b）所示，分别考虑了车辆三部分刚体与相互间的粘弹性连接关系。其中，车体-转向架、转向架-轮轴相互之间水平方向采用了弹簧和粘缸并联的稳定蠕变模式；轮对与路面之间水平连接采用弹性模式。模型系统可用于分析车辆沉浮、侧滚、点头、横移、横摇、艏摇等多自由度车辆三维动力响应。

2 车-隧耦合动力系统理论解

2.1 车辆动力学

根据车辆组构及其连接模式，为便于建立车-隧耦合动力系统，作如下基本假设：

①车辆的车体、转向架和轮对均认为是刚体，车辆就看作一个多刚体系统。

②车体与转向架之间由弹簧和阻尼器连接，称为“二系悬挂装置”，分别记做k2zC2z。

③转向架和轮对之间由弹簧和阻尼连接，称为“一系悬挂装置”，分别记做k1zC1z。

④车体考虑沉浮zc和点头自由度φc。

⑤转向架考虑沉浮和点头自由度ztiφti，i＝1，2，表示前后转向架。

⑥轮对看作刚体质量块，只有沉浮zwi，i＝1～4。

根据图2所示的车-隧耦合系统，分别建立车体振动方程、转向架动力方程、轮对振动方程，将各子系统动力方程集成即可获得系统的动力方程如式（1）。

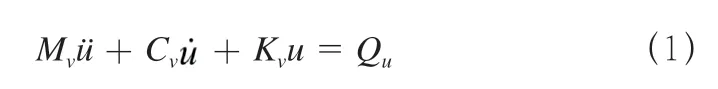
式（1）中：{u,,ü,Mv,Cv,Kv}分别为广义位移、速度、加速度、质量、阻尼和广义刚度。

2.2 动力方程基本解法

由于车辆为移动荷载，因此在本次分析中假设车辆以均匀的速度v行驶，不考虑车辆荷载对路面的冲击系数。为方便分析，假设在t=0时刻，车辆的四个轮对刚好已经全部作用到路面上，车辆的四个轮对之间的轮距分别为lw1,lw2,lw3,路面全长为Lb，因此车辆在路面上的运行时间为

取时间步长为Δt，则在t=nΔt时刻，各轮对作用的位置可同理确定；与各个路面单元的节点坐标作比较，判断出各个轮对分别作用于哪些单元上，即可按静力凝聚法分配至各个单元节点。对此2阶微分方程组，一般采用Newmark方法求解，取时间步长为Δt，在t=0时刻，取四个轮对和路面的相互作用力分别为车重的1/4，可将整个车体系统的所有位移自由度的初值求出，然后依次进行Newmark迭代。

2.2.1 变刚度动力方程的建立

在式(1)中，右边的荷载项为含有位移自由度向量的函数，即轮对和路面接触处的位移，并且由于任意时刻轮对和路面的作用点并不一定是路面单元的节点，因此要先将四个轮对作用点所在单元的位移按形函数分配到单元所在的八个节点上，然后将路面节点的位移移到方程的左边[K]Y项中，右边的荷载除了由路面不平顺引起的外部激励外，其他荷载项全部为零。空间六面体单元的插值函数可表示为：

若在nΔt时刻，Fwri(i=1,2,3,4)作用的位置可以确定，则轮对作用点所在单元的位移可以按以下方法分配到单元所在的八个节点上：

2.2.2 Newmark-方法迭代求解

Newmark-β方法中时间t+Δt的位移解答αt+Δt是通过满足时间t+Δt的运动方程：

2.3 车辆与路面随机脱离问题的移动坐标解法

实际问题中，车轮瞬时脱离路面的状态在所难免且跳离过程对轮下结构将产生冲击荷载。车轮跳离的时间区间内，汽车将以正常速度行驶，采用固定坐标系时很难描述车轮与路面的相互作用。本文采用速度与行车速度相同的移动坐标系建立车轮与路面瞬时脱离的力学求解方法。如图3所示。

图3 移动坐标求解轮路脱离方法

当Ki处于压缩即轮子没有脱离路面时，直接利用式（1）～（5）求解，当车轮跳离路面时：Ki=0，ρK=0.0，ρF=0.0修改式（1）对应的广义刚度和广义力阵，然后在移动坐标系中进行求解。

瞬时脱离，上、下子系统耦合作用通过不可拉伸弹簧Ki处理，系统振动方程组的刚度矩阵在没有脱离时处于耦合时变状态，而质量、阻尼矩阵不是时变的；当发生瞬时脱离时，刚度Ki值取为零，耦合作用消失。编写基于Newmark-法程序模块，嵌入通用程序，即可求解出具有本研究成果特点的动力结果。

3 参数分析

考虑客车是隧道中主要的行驶车辆，取有代表性的桂林大宇GDW6110H型号的客车作为模型中的车体，对路面不平度、行车速度的敏感性作概要分析。主要计算参数如表1所示。

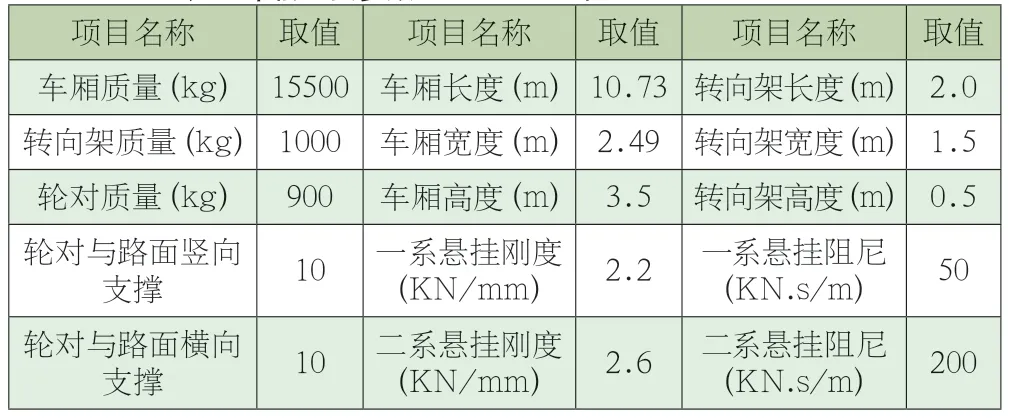
表1 车辆主要参数Table 1 Main parameters of vehicle

3.1 路面不平顺及其对系统振动影响

根据《车辆振动输入路面平度表示方法》（GB7031），取不平顺功率谱如式（14）

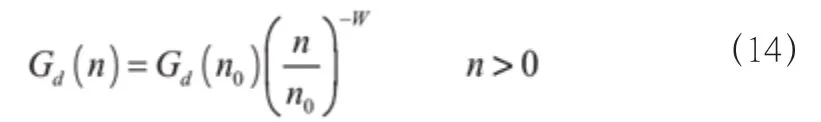
式（14）中：n—空间频率，m-1；n0—参考空间频率，n0＝0.1m-1；Gd(n0)—路面平度系数；Gd(n)—位移功率谱密度。设路面等级为A和B级，路面平度系数如表2所示。

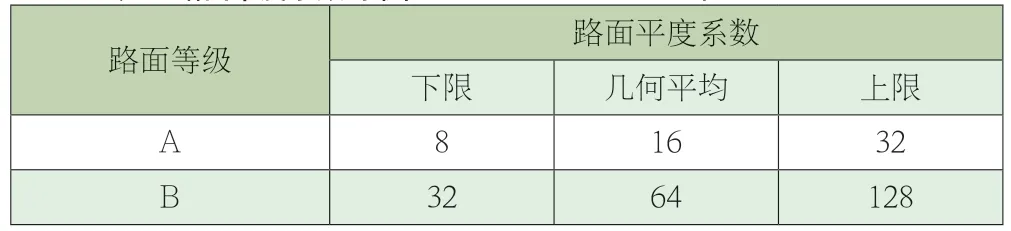
表2 路面平度系数的取值Table 2 Coefficient of pavement flatness

计算获得路面任一点振动加速度的时间分布，以车轮接触点为例，振动加速度随时间分布如图4所示。

图4 不同幅值下轮下点加速度时程

图4显示：（1）加速度幅值随路面不平顺幅值的增大而近似成比例增大；（2）当车辆进入取值点所在单元时各取值点加速度达到峰值，而后急剧减小，t≥1.0s，加速度接近于零。

3.2 行车速度对系统振动影响

计算获得车轮接触点振动加速度随时间分布如图5所示。

图5 不同车速轮下点加速度时程Fig. 5 Time history of point acceleration under different vehicle speed

图5显示，车速对系统各点振动幅值无影响，仅对幅值的时域分布有影响，产生相应的峰值点“滞后”现象。

4 案例分析

以深中通道为例，工程北距虎门大桥约30km，南距港珠澳大桥约3km，连接深圳和中山两市。路线西起深圳侧沿江高速公路机场互通，向西跨珠江口内伶仃洋海域，在中山马鞍岛登陆，止于横门互通，全长约24km。其中，海底隧道长6.845km，桥梁长约16.9km。隧道工程平面线位起于深圳侧东人工岛，线路自东往西先后下穿沿江高速、大铲航道、机场支航道、矾石水道，止于伶仃西航道和矾石水道之间的西人工岛。隧道断面为双向8车道，设计速度100km/h。

根据设计资料，取隧道断面结构模型如图6所示。

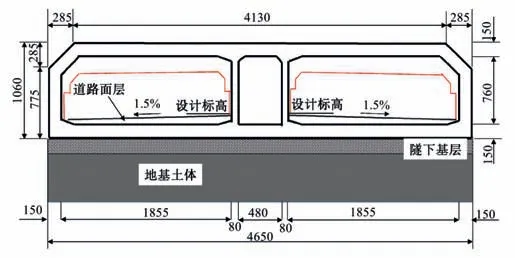
图6 深中沉管隧道断面结构示意图

考虑到深中通道为高速公路，最大载重车辆为大型客车，取表1相同的车辆参数。同时，计算中采用式（14）给出的道路不平顺功率谱，路面平度系数按A等级取值。

极限设计速度V=100km/s和路面不平顺幅值16mm条件下，计算获得轮下作用点的加速度时程并根据达兰贝尔方法获得相应点车辆动力荷载时程分布如图7所示。

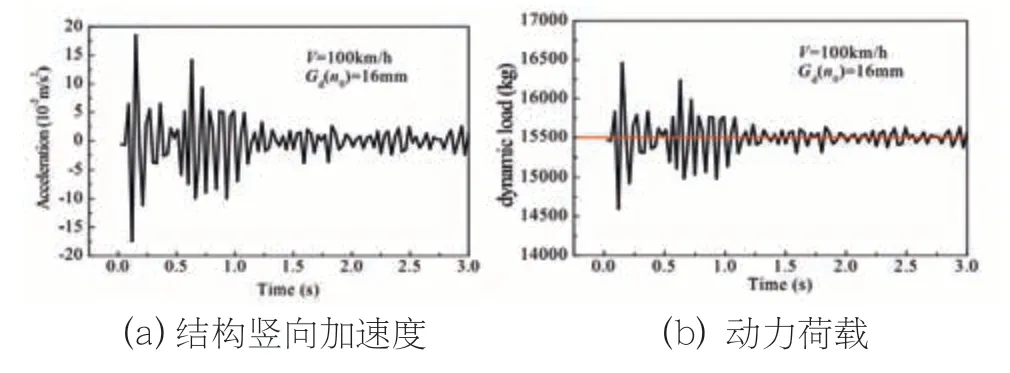
图7 隧道下部结构动力响应

图7显示：（1）当车辆进入取值点所在单元时该点的加速度达到峰值18×10-2m/s2，随后急剧减小，t≥1.2s，加速度接近于零；（2）当车轮进入取样点时，荷载振幅达到峰值，随后迅速衰减并于t=1.2s时收敛于车辆静载荷值；（3）车辆对隧道结构的动力荷载为车重与振动惯性力的叠加，最大冲击系数1.065；（4）荷载频率主要受道路不平顺功率谱的频率影响。

5 结论

比较系统地分析了路面不平顺、车辆行驶速度变化等不同工况条件下，车-隧系统动力响应及车辆动力荷载时变特性。结果表明：

（1）路面不平顺对整个系统振动特性有显著影响。随着路面不平顺幅值的增大，车体的位移和加速度都增大，而且其变化规律接近正比关系。但振动频率保持不变。

（2）行车速度对系统各点振动幅值无影响，仅对幅值的时域分布有影响，产生相应的峰值点“滞后”现象。无论何种参数取值，系统各部分振动加速度、车辆对隧道结构动力荷载的总体衰减规律变化不大。尤其对路面而言，车辆通过后相应参数呈负指数式迅速衰减。

（3）该研究所完成的建模及分析方法具有良好的普遍性和易拓展性，其模块的计算功能可方便地推广应用于其他三维刚-弹耦合分析的复杂动力学问题，对实际工程有一定的应用参考价值。