覆盖层影响下圆锥型瞬变电磁Occam 约束反演

李 哲，杨海燕，岳建华，刘志新，姜志海，苏本玉，张 华，汪 凌，杨夫杰

(1.东华理工大学 地球物理与测控技术学院，江西 南昌 330013；2.中国矿业大学 资源与地球科学学院，江苏 徐州 221116)

瞬变电磁法具有对低阻异常体敏感、体积效应小、野外施工效率高以及分辨率高等优点，被广泛运用于矿产资源勘探和深部构造调查等领域[1-3]。在煤矿巷道、工程隧道及地表浅层探测中，瞬变电磁法的多匝小回线装置应用较为广泛，在煤矿采空区、断裂构造探测中已取得较为明显的应用效果[4-6]。与之相比，圆锥型瞬变电磁发射装置具有互感影响小和浅层探测精度高等优势，对其持续开展的理论与应用研究具有重要的现实意义[7-10]。

在地面浅层瞬变电磁勘探中，覆盖层是影响瞬变电磁应用效果的重要因素之一[11-16]，为此，石显新等[11]研究了低阻覆盖层影响下瞬变电磁响应特征，验证了低阻覆盖层对瞬变电磁场的低阻屏蔽作用；杨海燕等[14]引入EA 参数，分析了地-井瞬变电磁勘探中覆盖层的影响规律。覆盖层的影响作用多出现在瞬变电磁采样时间的早期段，多数情况下晚期视电阻率公式难以体现这一时间段的覆盖层影响，全区视电阻率则可以产生较为突出的应用效果[17]。针对全区视电阻率转换问题，许多研究者开展了相关理论与应用研究[18-20]，其中，王华军[18]提出的全区视电阻率平移算法可以直接获得瞬变电磁各个采样时刻的视电阻率值，具有计算速度快、精度高，且具有唯一解等特点。

针对圆锥型场源瞬变电磁探测中的覆盖层影响问题，本文在不同参数模型建立的基础上，采用全区视电阻率计算方法求解视电阻率进行时-深转换，提出了地层厚度约束下的一维Occam 方法，分析覆盖层影响下圆锥型场源瞬变电磁响应特征及其对Occam 反演结果的影响。

1 圆锥型场源瞬变电磁全区视电阻率

式中：εi(t)为由第i匝线圈激励的感应电动势。

总磁矩保持不变，圆锥型场源装置随着高度增加、线圈间距增大、互感逐渐减弱。线圈间的互感[7]为：

由文献[18,20]可知，式(1)的响应曲线具有平移伸缩特性，具备采用平移算法计算全区视电阻率的前提条件。采用类似的方法求解式(3)，其响应曲线如图1 所示，从图中可知也具有平移伸缩特性，因而平移算法也适用于圆锥型场源瞬变电磁全区视电阻率计算。建立一个电阻率为1 Ω·m 的均匀半空间模型，由平移算法得到的全区视电阻率曲线(图2a)。由图2a 可以看出，全区视电阻率值在整个时间范围内都很好地逼近模型电阻率，且早期响应结果远好于晚期视电阻率。由此说明了平移算法在圆锥型场源视电阻率计算中的有效性。另一方面，对于如图2b 所示的KH 型四层介质模型，全区视电阻率结果刻画出了每层介质的电性特征，与传统的多匝小回线晚期视电阻率相比，在早期阶段有很大优势。

图1 不同电阻率的均匀半空间瞬变响应曲线Fig.1 Uniform half-space transient response curves for different resistivities

图2 晚期和全区视电阻率曲线Fig.2 Late and all-time apparent resistivity curves

2 基于光滑模型约束的一维反演

Occam 反演是高斯-牛顿法的变种反演方法[21]。通过模型范数(粗糙度函数)作为模型光滑约束条件，通过迭代不断搜索最小拟合差，在实现粗糙度最少的过程中保持反演稳定。根据Occam 反演理论[22]，粗糙度矩阵定义为：

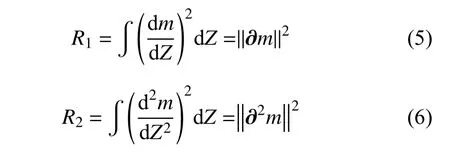
式中：m为 模型电性参数，Z为纵向搜索步长(厚度)，R1为一阶粗糙度，R2为 二阶粗糙度，∂ 是 一个N×N的粗糙度矩阵：

根据约束最小化理论，引入拉格朗日乘子λ-1得到无约束的目标函数：

式中：χ*为 给定的误差阈值，W为权值，d为观测数据，F[m]为对应观测数据的正演函数。

除拉格朗日乘子和雅可比矩阵以外，粗糙度函数也是影响拟合差的因素之一。粗糙度函数最优值选取受搜索步长Z和总搜索地层深度D控制，Z控制单个粗糙度函数值，D控制整体粗糙度矩阵的求解范围，粗糙度矩阵范围与实际探测区域吻合越好，则获得的反演效果越好。

其实中台化背后的核心理念还是平台化和生态化。它跟整个互联网20年来发展的脉络基本是一致的。当阿里在用平台化、生态化的方法推动整个电子商务生态健康发展时，最核心的是提供了各种各样的基础服务。但是要真正对外提供平台化的服务，企业就会发现面临一个重大挑战：内部的所有技术怎么变成服务？

研究发现，随着反演深度的增加，纵向搜索步长Z随之增大，且增长比例变大，进而导致地层界面分辨率降低[21-27]。另一方面，随着地层深度的增加，瞬变电磁场的扩散速度大于真实电磁信号的传播速度，导致相邻两层介质间的视电阻率极值的差值变小，地层界面收敛更加不明显。因此，需要结合钻探或其他地质资料，在特定厚度的层状地层条件下，对纵向步长和总搜索深度加以约束，进而提升反演结果的准确性。

纵向步长搜索公式和总搜索深度公式分别为：

式中：Z0为 初始搜索步长，Zi为 地层厚度的搜索范围，β为步长变化因子，i为搜索层数，N为搜索总层数，i=1，2，···，N。

结合地层分界面所处深度和已知地质信息，确定初始搜索步长和步长变化因子。当步长叠加深度与地层分界面深度较为吻合时，用最后一层界面深度控制粗糙度矩阵范围，同时使总搜索深度比最底层多1～2个步长。对于本文所建立的模型，浅层初始步长为0.5 m，变化因子为1.1，搜索层数和总搜索深度随约束模型变化。

3 模型试算

3.1 覆盖层介质模型

建立如图3 所示的平面分层覆盖层介质模型，在地表敷设顶、底半径分别为0.5、1 m 的圆锥型场源发射装置，接收线圈半径为1 m，其中模型第一层和第三层分别代表覆盖层和目标探测层，ρi和hi分别表示各层电阻率和厚度。同时，为方便模型试算过程中对试算结果进行论述，将覆盖层以下地层统一定义为下伏地层。

图3 层状介质模型Fig.3 Layered medium model diagram

为验证文中算法在圆锥型瞬变电磁数据反演中的有效性，分别运用视电阻率时深转换公式[20,28-29]、“烟圈”反演及Occam 反演计算出模型的视电阻率深度曲线和电阻率反演曲线。由图4a 可知，圆锥型瞬变电磁全区视电阻率曲线能反映出模型的电性特征，Occam 反演曲线在模型的第三层与真电阻率的吻合程度更高。经地层厚度约束后(图4b)，在未增大覆盖层电磁响应的情况下，第二、第三层对应的电阻率曲线与模型电阻率更为吻合，由此验证了加地层信息约束的Occam 反演方法在圆锥型瞬变电磁数据反演中的有效性。

图4 KH 型地电模型反演曲线Fig.4 KH type geoelectric model inversion curves

基于前述分析，通过控制覆盖层单一参数变化，进而研究覆盖层电阻率大小和厚度对圆锥型瞬变电磁探测的影响。

在研究覆盖层电阻率大小对探测产生的影响时，探测目标层为第三层，覆盖层厚度h1固 定为20 m，ρ1设为ρ3的 倍数，同时使覆盖层电阻率ρ1分别满足小于、大于、等于ρ2和ρ3。当覆盖层电阻率与下伏地层电阻率满足ρ1=ρ2时，将之视为均匀半空间三层介质。

图5a、图5b 分别对应覆盖层介质模型下目标层为低阻的全区视电阻率时间曲线和反演电阻率深度曲线。如图5a 所示，覆盖层电阻率越低，需要更长的采样时间才能观测到下伏地层的异常响应。覆盖层电阻率低于目标层电阻率时，视电阻率呈缓慢升高趋势，中间高阻地层视电阻率远小于模型电阻率，目标层低阻异常响应不明显。随着覆盖层电阻率升高，瞬变场扩散至低阻目标层时，视电阻率曲线发生明显畸变、异常响应越清晰。由图5b 可知，在覆盖层电阻率小于目标层电阻率时，反演计算的目标层低阻响应效果依旧不理想，这表明覆盖层电阻率越低，低阻屏蔽效应越强。当覆盖层电阻率等于目标层电阻率时，覆盖层为低阻，其低阻响应较目标层低阻响应突出。随着覆盖层电阻率增大，下伏地层反演电阻率峰值对应深度下移，目标层反演电阻率与模型拟合度呈现先提升后减弱现象。覆盖层电阻率等于下伏高阻地层电阻率时为临界点，该条件下目标层电阻率与模型最吻合。此后，覆盖层电阻率继续增大，目标层电阻率与模型拟合度降低。通过约束反演，反演电阻率值与模型真实电阻率更加吻合，且于目标层界面处电阻率收敛快，层界面分辨率高。

当目标层为高阻时，覆盖层电阻率变化对于高阻目标地层探测效果的影响情况与上述低阻模型基本一致(图5c、图5d)。覆盖层电阻率与下伏高阻地层电阻率比值增大，经反演处理目标层反演电阻率与模型拟合度亦呈现先提升后减弱现象。

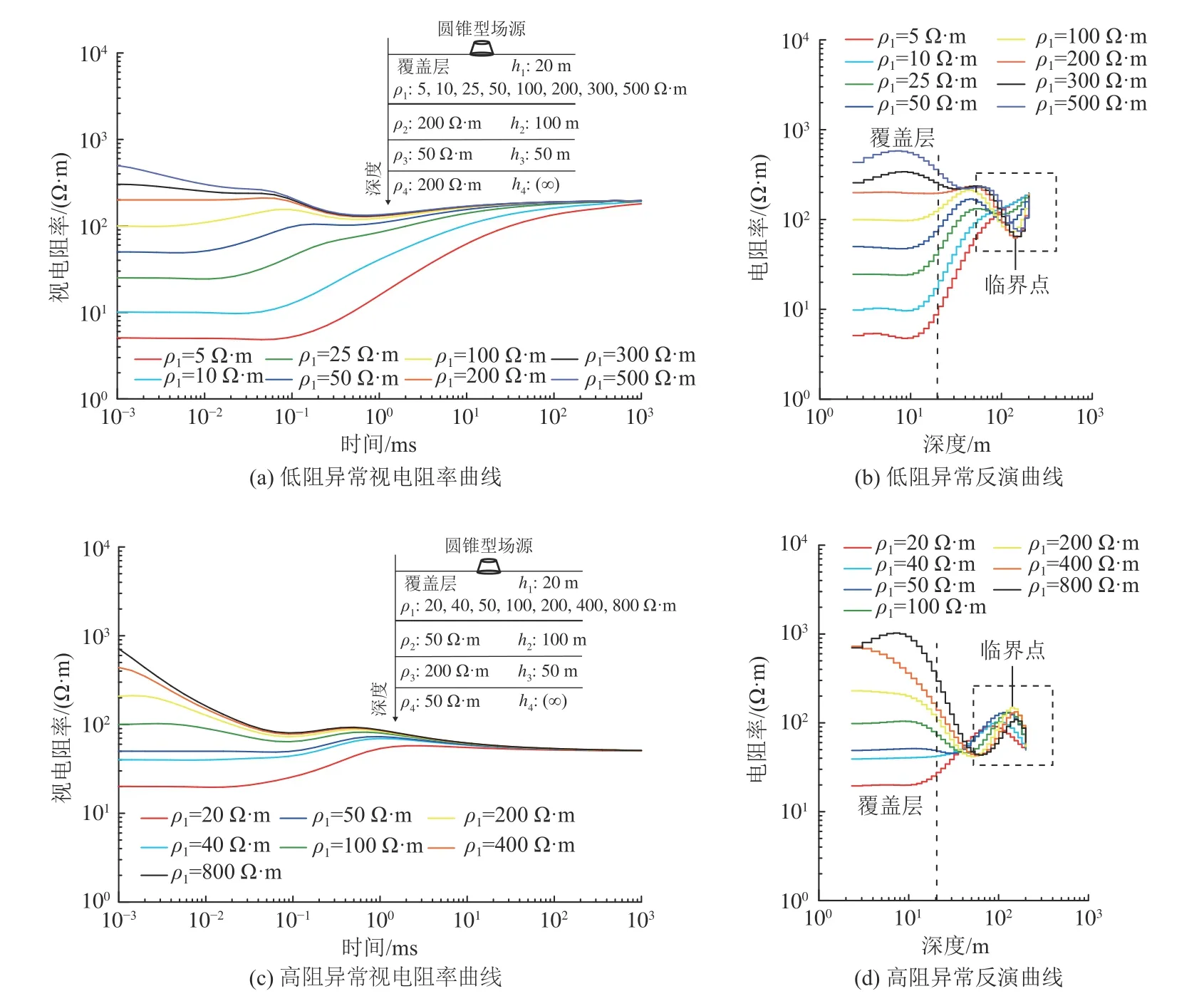
图5 覆盖层电阻率变化探测效果对比Fig.5 Comparison of the detection effect during the overburden resistivity change

ρ1为 100 Ω·m、h1变化时，覆盖层厚度对圆锥型瞬变电磁探测效果的影响如图6 所示。随着覆盖层厚度增大，目标层埋深随之增大，此时下伏地层电磁响应减弱。覆盖层厚度越小，目标层异常响应越强，视电阻率及反演电阻率峰值与模型真实电阻率更加吻合。

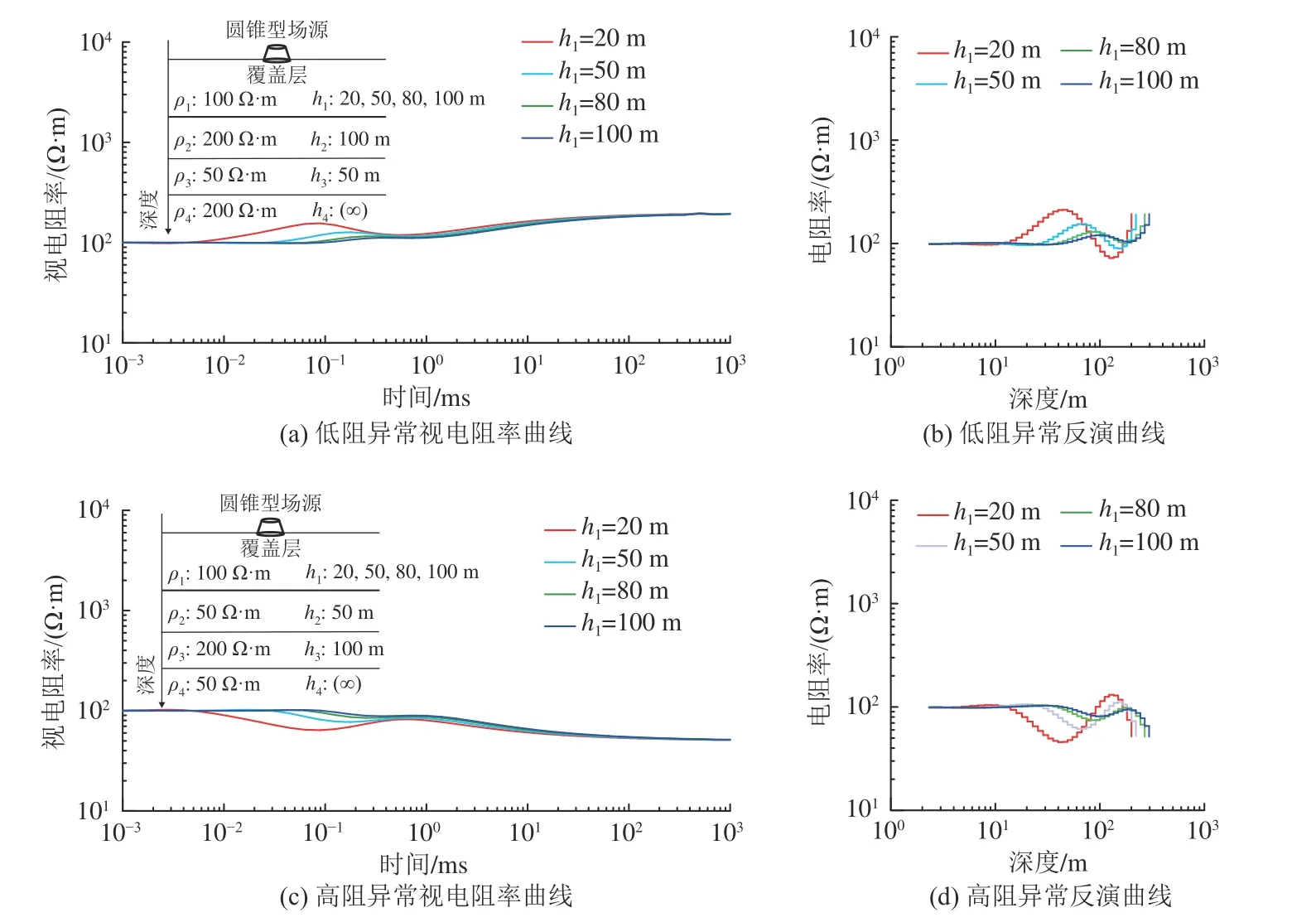
图6 覆盖层厚度变化探测效果对比Fig.6 Comparison of the detection effect of overburden thickness change

根据电磁波传播理论可知，随着电磁波传播距离增大，电磁波强度逐渐衰减，因此，目标层埋深成为影响探测效果的因素之一。保持目标层埋深为150～250 m，即h1+h2=150 m，覆盖层厚度变化对探测效果的影响如图7 所示。覆盖层厚度增大，全区视电阻率曲线趋于平滑，异常响应不明显，目标层电磁响应峰值出现时间提前，反演计算电阻率峰值对应深度下降，通过约束反演，电阻率拟合效果提升与所设模型吻合。覆盖层厚度增大，对相同埋深下目标层电阻率反演结果未产生明显影响。

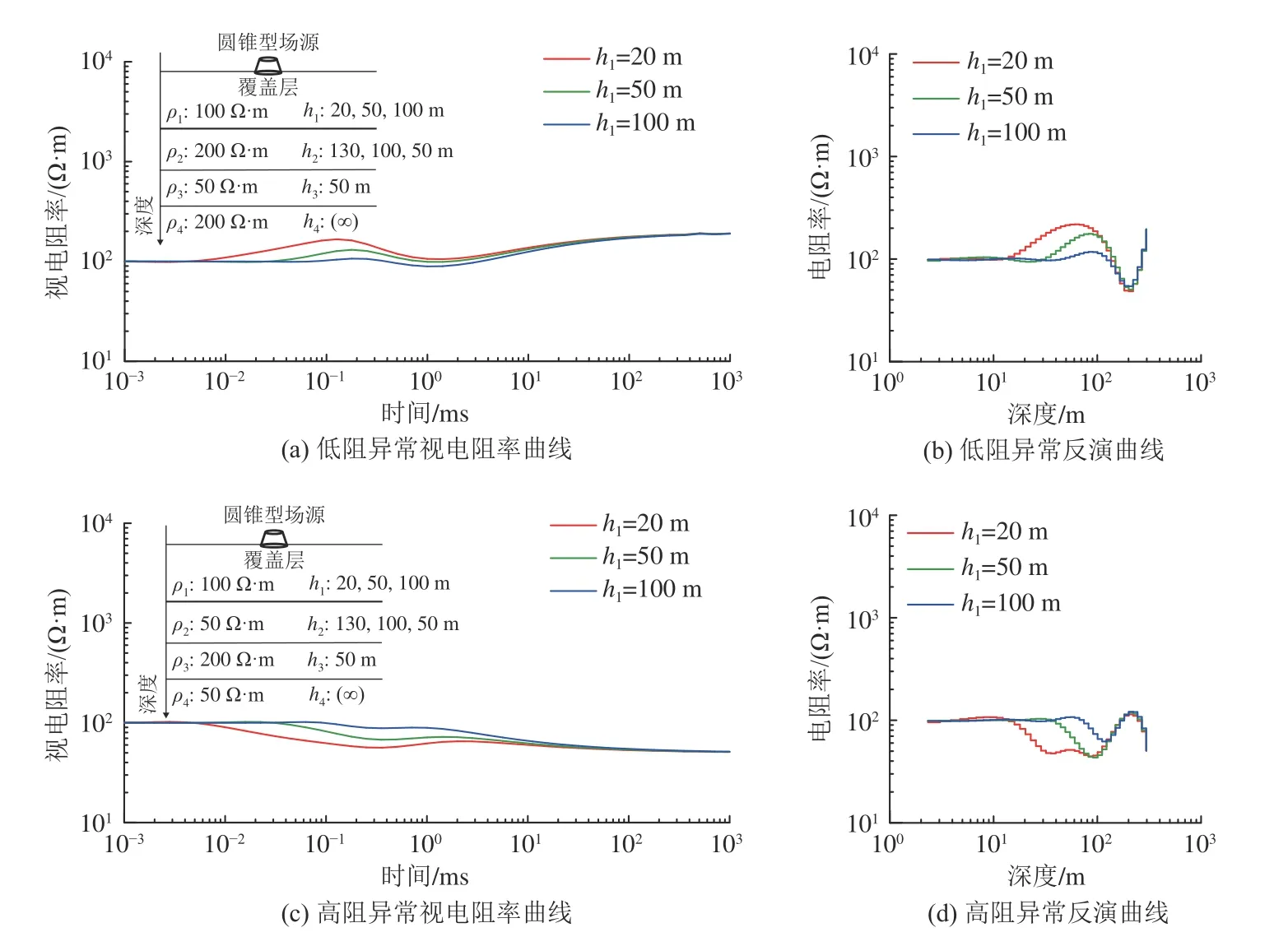
图7 目标层埋深固定时覆盖层厚度变化探测效果对比Fig.7 Comparison of detection effect of overburden thickness change with a fixed target layer depth

3.2 典型低阻体模型

建立一个低阻异常拟二维模型，异常体横向分布从横坐标60 m 到100 m，埋深为70 m；覆盖层厚20 m，电阻率50 Ω·m，其他参数如图8a 所示。测线点距5 m，共33 个测点。圆锥型发射装置顶、底部半径为r1=0.5 m、r2=1 m，发射线圈11 匝。图8b 为模型的全区视电阻率拟断面图，图中覆盖层与高阻围岩分界面在20 m 处与模型吻合，中间高阻围岩区域受上覆低阻覆盖层和下伏低阻异常影响，响应效果较差。在横坐标65～95 m、埋深60 m 区域存在低阻异常，由于瞬变电磁具有低阻屏蔽效应，异常区域顶、底部高阻不明显，视电阻率增长速率较慢，地层界面分辨率低。图8c 是运用加地层约束Occam 反演算法计算得到的拟二维模型电阻率剖面，从图中可以发现，低阻异常区域范围较为明显，且与模型中的异常区域吻合。与全区视电阻率拟断面图对比可知，反演后覆盖层下伏高阻围岩与低阻异常界面的分层效果明显提升，有效地削弱了由低阻覆盖层所带来的低阻屏蔽影响。

图8 拟二维模型全区视电阻率及Occam 反演剖面对比Fig.8 Comparison of all-time apparent resistivity of imitate-2D model and Occam inversion profile

4 实测资料反演

为了验证圆锥型瞬变电磁探测技术和反演算法的有效性，在江西抚州某实习基地开展了试验研究，并将得到的研究结果与EH4 大地电磁反演结果进行了对比。试验测线总长150 m，点距5 m。试验仪器采用澳大利亚生产的Terra TEM 瞬变电磁仪，发射场源顶部半径15 cm，底部半径32.5 cm，高度0.5 m，发射线圈172 匝，接收线圈半径32.5 cm，匝数为41 匝。

根据已知地质资料[30]，试验区域浅层为第四系覆盖层，下伏地层主要为前震旦系板溪群下亚组、石炭系下统华山岭组、梓山组，测区横跨一条NE 向正断层和一条SW 向小断层，均从属于温泉断层。在图9 所示的EH4 音频大地电磁反演结果中，测线区域下部存在3 个低阻异常区域(图中A、B和C所在位置)。从图10 可以看出，瞬变反演电阻率剖面所揭露的低阻异常与EH4 结果近似吻合，异常响应程度与相对位置基本对应。结合已有地质资料，推测异常区域A、B和A、C之间为2 条断层。

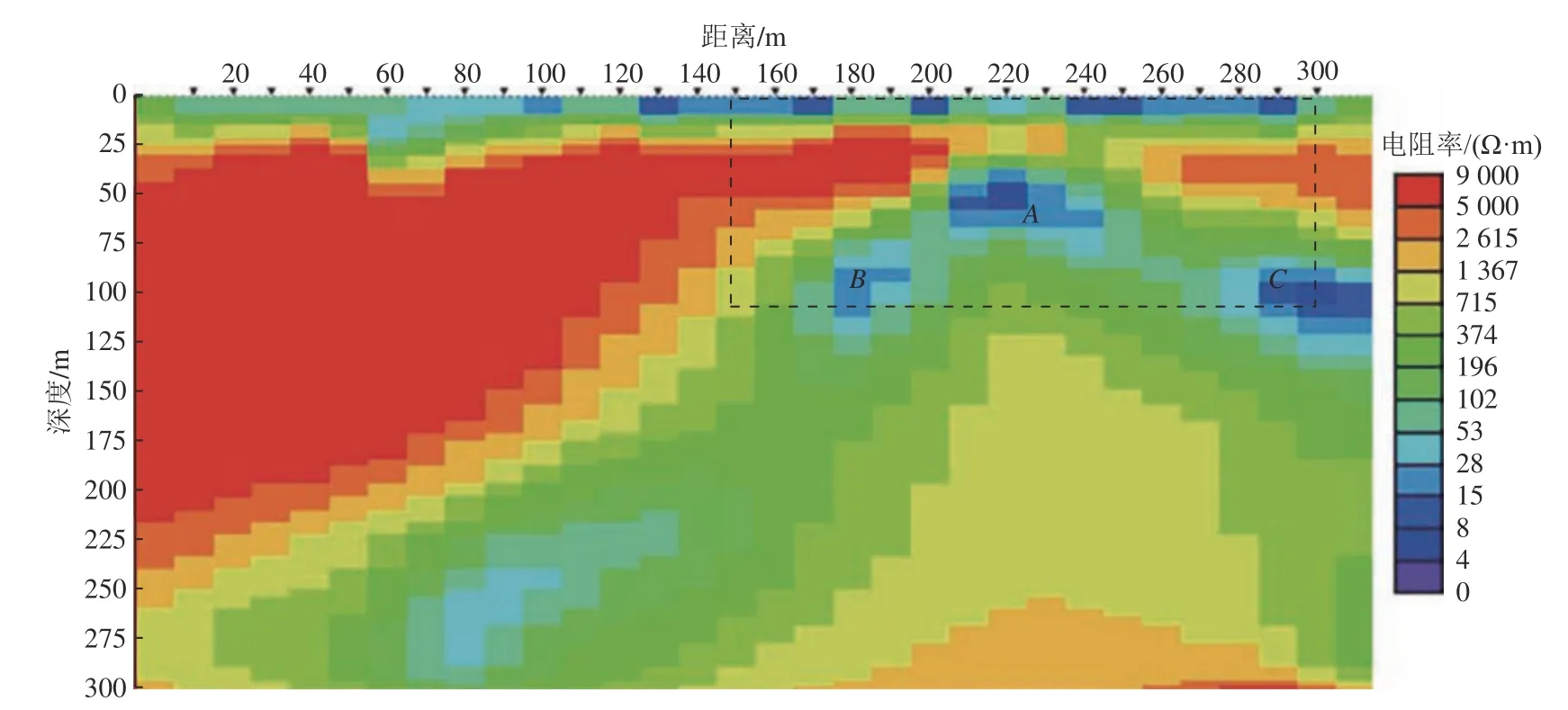
图9 EH4 大地电磁反演剖面[31]Fig.9 EH4 magnetotelluric inversion profile[31]

图10 圆锥型瞬变电磁反演剖面Fig.10 Cone-shaped transient electromagnetic inversion profile

5 结 论

a.目标层电磁场瞬态响应强度主要与覆盖层和目标层电阻率比值有关。覆盖层电阻率增大，观测到目标层响应所需观测时间减小、强度提升，目标层反演电阻率与模型拟合度呈先增大后减弱趋势。当与目标层电阻率相同时，覆盖层响应较为突出。覆盖层厚度增大，下伏地层响应相应减弱，但对相同埋深下反演结果影响不大。

b.结合模型约束的Occam 反演结果与实际模型电阻率较为吻合，地层界面的分辨率和电阻率收敛速度均有较好提升。

c.圆锥型瞬变电磁探测可以很好地刻画出异常区域的空间分布及形态特征。

致谢：重庆大学电气工程学院徐正玉博士对文中算法设计提供了帮助，审稿专家和本刊编辑对论文撰写提出了宝贵意见，作者一并致谢！