飞艇纵向动导数计算方法研究

高攀 GAO Pan

（中国特种飞行器研究所，荆门 448035）

0 引言

动导数是飞行器动态特性分析的必要数据，是飞行品质分析的重要依据。目前对动导数获取方式主要包括飞行试验、风洞试验、工程估算、数值计算等方法[1]。飞艇与飞机气动外形和飞行原理都有较大差别，针对飞机的动导数工程估算方法并不适用于飞艇；飞行试验和风洞试验代价高昂、试验周期长；CFD方法与飞行试验、风洞试验相比，具有经济性高、无支架干扰等优点，利用CFD求解飞艇动导数已经成为一个重要研究方向。国内对飞行器动导数计算开展了大量的研究，陶洋、范召林[2]等采用求解ALE形式RANS方程计算了带控制舵导弹俯仰和滚转动导数；伍彬、陆韵[3]等采用基于N-S方程的数值模拟技术对俯仰动导数计算方法进行了研究，研究了时间步长、内迭代次数、强迫运动幅值、减缩频率对俯仰动导数计算结果的影响；孙涛、高正红[4]等重点分析了减缩频率对动导数计算的影响，提出了利用CFD进行动导数计算时减缩频率的选择原则。国外也对飞行器动导数数值计算方法开展了很多研究[5-6]。本文首先采用俯仰振荡法对国际标模Finner导弹进行动导数计算，并将计算结果与风洞试验结果进行对比，验证动导数CFD求解的准确性；然后针对某飞艇开展CFD计算，采用俯仰振荡法和旋转流场法求解纵向单独动导数，为飞艇动导数的获取提供一种新的思路。

1 动导数CFD计算方法

1.1 纵向组合动导数计算方法

飞艇俯仰组合动导数是指俯仰力矩对俯仰角速度和俯仰力矩对迎角变化率的导数之和，可以通过模拟飞艇纵向俯仰振荡获取，假定飞行器绕重心俯仰振荡方程为：

式中：θ为俯仰角，θ0为初始迎角，θm为振幅，ω为振荡角频率。

因此俯仰角速度可以写为：

从飞艇运动状态可知，飞艇迎角等于俯仰角，迎角变化率等于俯仰角速度，即：

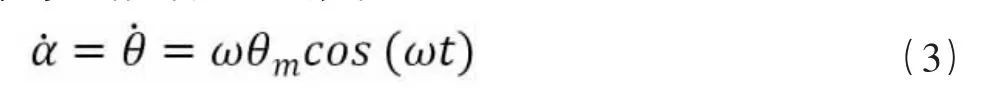
飞艇俯仰力矩系数通过泰勒展开可以写为：

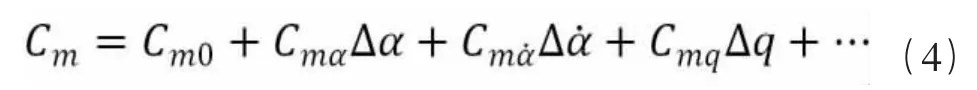
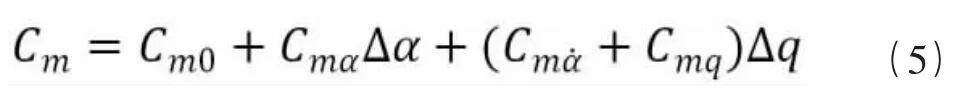
带入表达式（1）和（2）可以得到如下形式：

式中：Cm0为初始力矩，Cmα为纵向静导数，Cmα˙为俯仰力矩对迎角变化率的导数，Cmq为俯仰力矩对俯仰角速度的导数，Cmα˙+Cmq为纵向组合动导数。

从俯仰力矩的表达式可以看出，非定常模拟时间足够长时，俯仰力矩表现出和俯仰振荡相同的周期性。

本文采用最小二乘法对纵向组合动导数进行参数辨识：根据纵向力矩的周期性，得到力矩周期性数据，并通过数据拟合得到如下表达式：

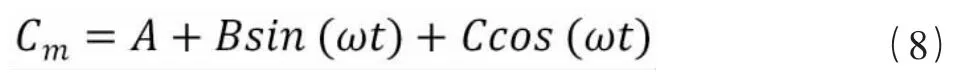
由此，通过拟合曲线可以辨识出纵向组合动导数为：

升力系数组合动导数可采用类似方法求解。

1.2 纵向单独动导数计算方法

飞艇纵向单独动导数包括俯仰力矩对俯仰角速度的导数Cmq和俯仰力矩对迎角变化率的导数Cmα˙。对于Cmq，可以通过旋转流场法获取，结合式（9）获取的组合动导数，进而可以得到Cmα˙。

旋转流场法即模拟飞艇的定常拉升运动，定常拉升运动是指飞艇在铅锤面内做角速度不变的圆周运动，由于速度始终沿着圆周的切线方向，故运动中迎角保持不变，俯仰角不断变化。如果选择固连在飞艇上的坐标系，相对该坐标系流动就是定常的，因此可以进行定常计算。

如图1所示，保证飞艇速度不变，给定飞艇不同的运动角速度，可得到不同的俯仰力矩系数，俯仰阻尼导数表达式为

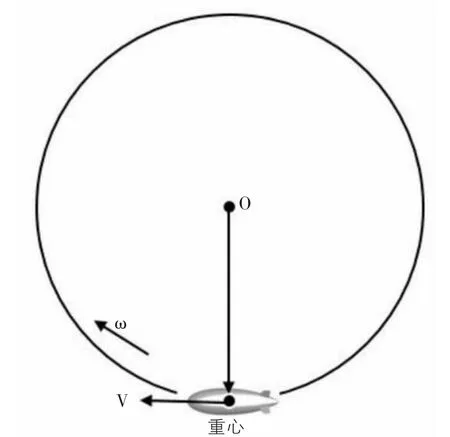
图1 飞艇定常拉升运动

1.3 数值计算方法

计算采用非结构瞬态滑移网格，滑移网格整个计算域分为静止区域和滑移区域，两个计算区域通过交界面interface进行数据传递，滑移区域整体相对静止区域进行旋转，运动过程中计算网格质量不发生改变，非常适合飞行器的非定常气动计算。

控制方程为雷诺平均NS方程，湍流模型选用Realize k-e模型，k-e模型适合旋转流动、强逆压梯度的边界层流动、流动分离等情况，算法为simple算法，压力项、对流项采用二阶迎风格式离散，扩散项采用中心差分格式离散。

2 计算结果分析

2.1 Finner标模验证

2.1.1 计算模型与计算条件

计算采用国际标模Finner导弹模型，模型尺寸如图2所示，模型重心到头部距离为5d，d为弹体直径。

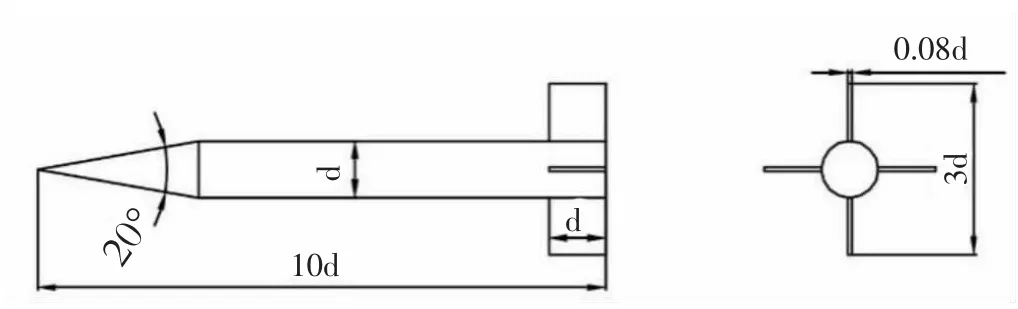
图2 Finner导弹模型

计算采用非结构六面体笛卡尔网格，y+在1左右，网格质量良好。采用非定常计算，计算Ma取风洞试验马赫数1.58，减缩频率k取0.05，振荡幅值取1°，初始迎角为0°。

2.1.2 计算结果分析

图3是迎角和俯仰力矩系数一个周期内随时间变化曲线，可以看出迎角和俯仰力矩系数存在相位差，具有迟滞效应。图4为俯仰力矩系数迟滞环计算结果与文献[5]计算结果的比较，可以看出，计算迟滞环曲线与文献[5]基本一致。

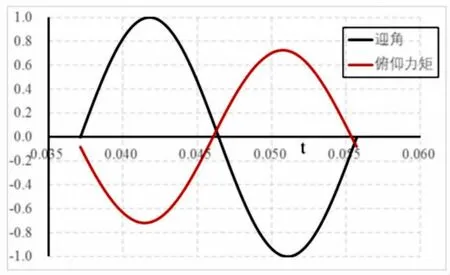
图3 俯仰力矩系数与迎角随时间变化曲线

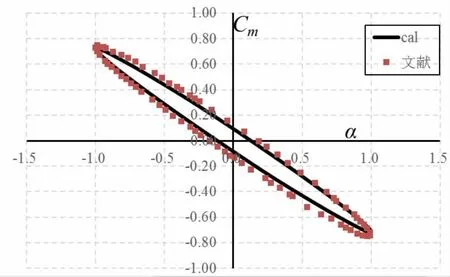
图4 俯仰力矩系数迟滞环曲线

表1为本文计算结果与风洞试验结果的对比，可以看出纵向和横航向动导数计算结果与试验结果误差在5%以内，表明本文计算方法可靠，动导数计算精度较高。

表1 纵向动导数计算结果

2.2 飞艇动导数计算

2.2.1 计算模型与网格

计算对象为某型飞艇，计算模型和计算网格如图5，计算网格采用非结构六面体笛卡尔网格，网格质量良好。静止区域和滑移区域网格总数为430万，计算模型周围流场以及尾流区均进行了不同程度的空间加密处理，不仅保证网格尺寸空间增长的均匀过渡，又能对尾流进行较好的捕捉。

图5 计算模型和网格

2.2.2 计算条件

计算条件为标准海平面大气条件，计算初始迎角为0°，速度20m/s，参考长度50.176m，参考面积260.3m2，采用非定常计算。飞艇纵向低频小振幅运动规律为：，振荡频率为1Hz，振荡中心为飞艇重心，飞艇的俯仰振荡通过编写UDF实现。

2.2.3 计算结果及讨论

图6为采用俯仰振荡法计算飞艇一个周期内俯仰力矩系数随计算迎角的变化曲线，即迟滞环。迟滞环为逆时针即非定常气动力做负功，纵向组合动导数为负值。

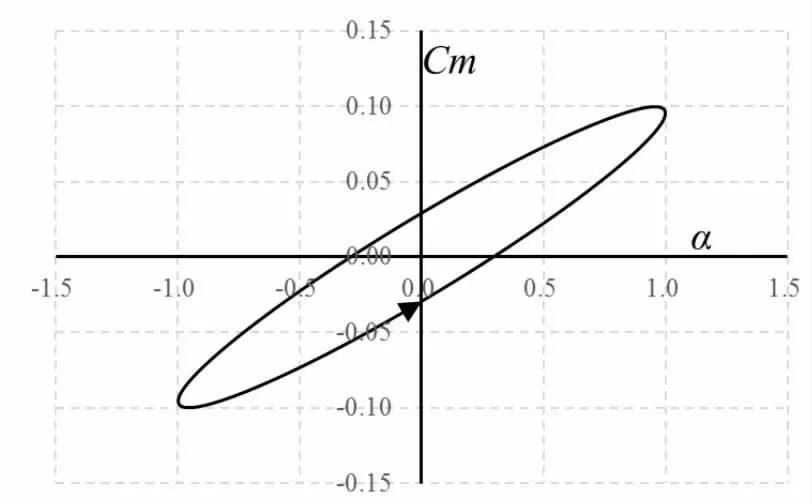
图6 迟滞环

给定飞艇无量纲化角速度分别为0.2189、0.4378、0.6568，图7、图8分别为俯仰力矩系数和升力系数随俯仰角速度变化曲线。可以看出，俯仰力矩系数和升力系数随俯仰角速度增加线性变化，通过线性拟合即可得到Cmq和CLq。

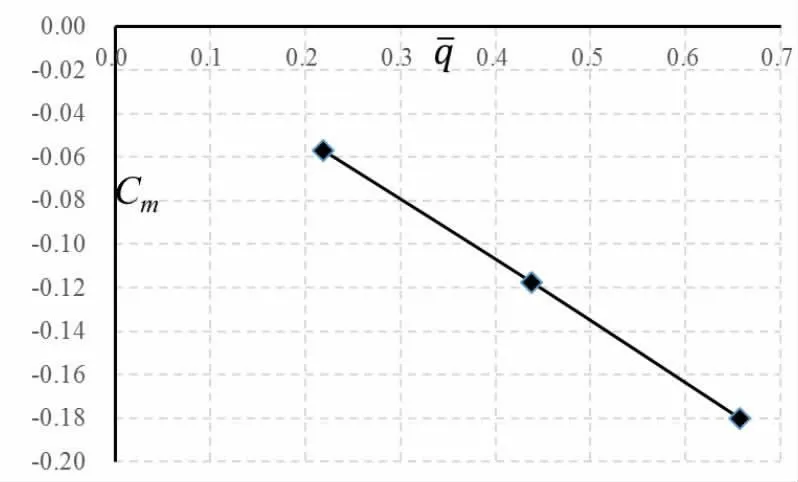
图7 俯仰力矩系数随俯仰角速度变化

图8 升力系数随俯仰角速度变化

表2为0度迎角下，飞艇纵向组合动导数和单独动导数数值计算结果。

表2 纵向动导数计算结果

由此可见，通过俯仰振荡法和旋转流场法可以获得飞艇纵向组合动导数和单独动导数，横航向动导数也可通过类似的方法获取。由于飞艇和飞机气动外形差别较大，现有的飞机动导数工程估算法并不适用飞艇，而俯仰振荡法和旋转流场法是飞艇动导数求解的有效方法，具有较高的工程应用价值。

3 结论

本文利用俯仰振荡法对国际标模Finner导弹进行了动导数计算，并将计算结果与风洞试验结果进行了对比。利用俯仰振荡法和旋转流场法对某型飞艇纵向组合动导数和单独动导数进行了计算，得到主要结论如下：①通过俯仰振荡法对Finner导弹动导数进行了数值计算，计算结果与风洞试验结果进行了对比，误差在5%以内，说明本文数值方法的正确性。②通过俯仰振荡法和旋转流场法可以获得飞艇纵向组合动导数和单独动导数，为飞艇动导数的获取提供一种新的思路，具有较高的工程应用价值。