多品种燃油海运库存路径问题鲁棒优化模型与算法

杨华龙，吴艳华，孙奕伦

(大连海事大学，交通运输工程学院，辽宁大连 116026)

0 引言

船用燃油(简称燃油)供给是海上船舶营运的重要保障，随着我国海上各类经济活动日益频繁，燃油需求出现快速增长的趋势。由于海上运营船舶类型众多，不同船型加注的燃油品种不尽相同，且加油量差异较大，沿海各港口燃油库存合理化，以及海运配送路径优化均成为燃油供货商的核心决策问题。因此，在海运供应链的供货商管理库存(Vendor Managed Inventory,VMI)模式下，研究多品种燃油MIRP具有重要的现实意义。

MIRP属于海上工业船运输中的库存和货运集成问题[1]，如沿海供应的燃油、化学品、液化天然气(LNG)等类货物均存在MIRP。相比于一般库存路径问题(Inventory Routing Problem,IRP)，MIRP 具有发船周期固定而路径变动等更为复杂的海运供应链特征。国内外学者关于MIRP 展开了许多深入研究。Goel等[2]针对LNG二级海运供应链，在考虑生产、消费和航行时间等季节性变动下，建立了MIRP 优化模型，解决单类货品的海运库存和路径优化问题；在此基础上，Agra 等[3]采取专用舱室策略，拓展研究构建了多品种燃油MIRP 优化模型，解决不能混装的多类货品舱室配载问题；Misra等[4]则进一步提出同一舱室在不同航次装载不同油品的非专用舱室配载策略，建立了多类油品多航次MIRP优化模型。

然而，不确定性是许多VMI 问题的固有属性，在海运供应链中，货品供需及海运过程均存在各类不确定性因素。Cho等[5]研究了极端天气影响下装卸时间不确定的LNG 供应链，建立装卸时间概率分布已知情形下的两阶段随机MIRP 优化模型。Dong 等[6]进一步考虑租船市场波动和货品生产/消费速率变化等不确定性因素，在假设不确定性因素均服从正态分布的条件下，构建滚动时域再优化随机MIRP模型。Agra等[7]针对船舶航行和在港时间不确定下的多品种燃油分销海运供应链问题，建立基于离散分布律已知情景下的两阶段随机MIRP模型。但上述考虑随机不确定性因素MIRP 模型均是在随机因素概率分布已知条件下，以期望值优化作为决策目标，这类模型一方面利用概率期望值决策所得优化解的稳定性一般较差；另一方面，对于随机因素概率分布未知的场景并不适用。为此，刘炬等[8]针对需求不确定下单品种燃油供应问题，建立了MIRP 鲁棒优化模型，并设计了将二次锥模型拆分和转化的两阶段分解算法。然而，在面对需求不确定下多品种燃油供应问题时，该研究成果要想做到满足客户服务水平要求、低成本的燃油供应也绝非易事，具体体现在：①由于船舶挂靠港口成本高且靠泊过程时间较长，在多品种燃油供应时，需求港的每种燃油配送通常只允许一艘船舶完成，即不能使用多条船为同一港口配送同一品种燃油，但多品种燃油配送任务可由一艘或多艘船舶完成；②当各港口各品种燃油需求不确定且其概率分布未知时，供货商无法利用客户服务水平确定各港口各品种燃油的最大库存水平阈值，而只能对多品种燃油MIRP加以鲁棒优化；③由于各品种燃油需求的随机波动性，供货商需要根据需求变动情况，采用灵活的舱室装载和船舶配送路径方案，以便更有效地降低配送成本。

有鉴于此，本文针对需求不确定且概率分布未知情形下的多品种燃油沿海供应问题，提出一种设置各需求港口各品种燃油航次累积不确定需求预算阈值约束的方法，以实现MIRP 鲁棒优化的现实要求。本文的主要贡献如下：结合需求不确定且其概率分布未知下的多品种燃油二级海运供应链特点，提出非专用舱室和非固定停靠港的船舶配送策略；通过设置各需求港各品种燃油航次累积不确定需求预算阈值，构建多品种燃油MIRP 非线性鲁棒优化模型；将自适应大邻域搜索(Adaptive Large Neighborhood Search,ALNS)算法和Gurobi 求解器嵌入自适应遗传算法(Adaptive Genetic Algorithm,AGA)中，设计改进混合自适应遗传算法(Hybrid Adaptive Genetic Algorithm,HAGA)，提升了算法的求解质量和效率。

1 问题描述

考虑一个含有多个供应和需求港口的燃油二级海运供应链系统，各供应和需求港口的燃油品种不尽相同。如中国船舶燃料供应公司在大连、天津等港口建设大型油库以满足环渤海区域的燃油需求，其中，天津港主要供应4#(油品1)和120cst(油品2)燃油，大连港主要供应180cst(油品3)和380cst(油品4)燃油。为了满足决策期内海上运营船舶的各品种燃油需求，供货商基于定期(固定的发船间隔期)补货策略，安排多艘不同类型且含多个非专用舱室的配送船舶，将各品种燃油从供应港口配送到各个需求港口。发船间隔期可由船舶完成一个航次配送任务的时间确定，故可将决策期等分为若干个航次时间(简称航次)。

鉴于运输安全需要，燃油运输船舶都拥有多个密闭隔离的燃油装载舱室。故在船舶不同航次的燃油配送时，供货商可根据各港口各品种燃油的需求情况，灵活地制订船舶舱室配载方案，即供货商可以采取非专用舱室配送策略，在不同航次船舶舱室可以装载不同品种的燃油。另外，鉴于挂靠港口时间和成本因素，船舶每航次最多只能挂靠同一港口一次，且配送船舶从某个供应港口出发，完成航次配送任务后可就近返回任一供应港口，即船舶无固定停靠的专属供应港口，由此形成的某航次船舶多品种燃油配送路径如图1所示。

由图1 可知，在某个航次，供货商根据各需求港口上期末燃油的剩余库存量及本期的需求预测值，船舶1从大连港出发，装载燃油品种3和4，沿途为丹东港、威海港、烟台港、龙口港、黄骅港、唐山港和秦皇岛港配送燃油，最后返回天津港。同时，船舶2 从天津港出发，装载燃油品种1 和2，沿途为龙口港、烟台港、黄骅港、唐山港、秦皇岛港和营口港配送燃油，最后返回大连港。

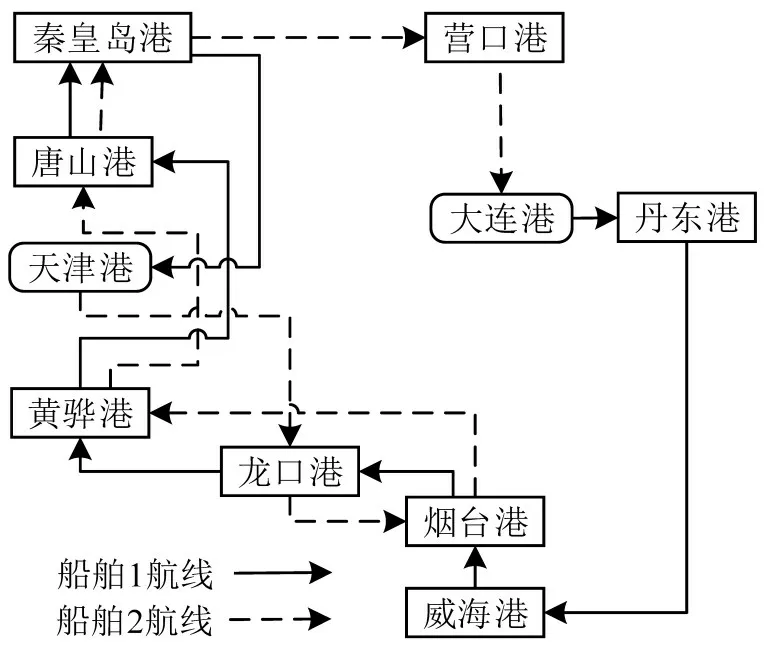
图1 多品种燃油配送路径Fig.1 Distribution routing of multi fuel products

在需求不确定下，IRP 优化目标是实现供货商库存与配送总成本最小化，其前提条件是要满足客户服务水平(即各需求港各品种燃油的可获得性概率水平)要求[9]。然而，由于受海上各类经济活动、天气海况等多种复杂因素的影响，各港口各品种燃油需求随机波动性较大且难以获取较为准确的概率分布规律[10]。因此，当各港口不同品种燃油需求概率分布未知时，供货商无法利用设定的客户服务水平对多品种燃油MIRP 进行优化决策。此时，根据随机需求下的风险控制原理，供货商可结合自身的风险厌恶程度，确定各港口各品种燃油保守系数(即衡量决策者对风险偏好程度的系数，其受决策者的主观因素影响，取值范围为区间[0,1]，通常可采用风险效用等理论方法加以测度，决策者对风险越厌恶，则保守系数取值越大)，设置航次累积燃油不确定需求预算阈值，据此建立满足各港口各品种燃油不确定需求预算的约束条件，构建多品种燃油MIRP鲁棒优化模型。

综上，多品种燃油MIRP 鲁棒优化的实质便是，供货商根据船舶完成一个燃油配送任务的航次时间，将决策期划分为若干个航次，针对各港口各品种燃油的不确定需求，采用非专用舱室和非固定停靠供应港的船舶配送策略，通过设置保守系数，对多品种燃油的库存路径方案进行优化决策，确定船舶在供应港各航次各舱室配载的各品种燃油量，向各需求港配送量，以及海上配送路径，以实现决策期内供货商燃油库存与配送总成本最小化的目标。

为了便于问题求解，本文结合实际做以下假设：

(1)在VMI 模式下，供货商管理燃油库存与配送，不考虑需求港管理情形；

(2)供应港各品种燃油储备充足；

(3)各港口各品种燃油各航次需求的概率分布未知，但需求均值和最大偏离值已知；

(4)船舶发船间隔期确定，决策期是航次的整数倍。

2 模型构建

2.1 参数及变量符号

(1)集合

Δ——供应港集合，Δ={1,2,…,M}，其中，M为供应港总数；

Ω——需求港集合，Ω={1,2,…,N}，其中，N为需求港总数；

Θ——船舶集合，Θ={1,2,…,V}，其中，V为船舶总数；

Ψ——燃油品种集合，Ψ={1,2,…,K}，其中，K为燃油品种总数；

Φv——船舶v(v∈Θ)隔离油舱集合，Φv={1,2,…,Lv}，其中，Lv为船舶v舱室总数；

Γ——决策期内航次集合，Γ={1,2,…,T}，其中，T为航次总数；

Uikt——需求港i(i∈Ω)燃油k(k∈Ψ)航次t(t∈Γ)需求取值集合。

(2)参数

Vv——船舶v的航速(kn)；

Wvl——船舶v舱室l(l∈Φv)最大载重量(t)；

E——发船间隔期(d)；

Qik——需求港i燃油k最大库存水平(t)；

Dikt——需求港i燃油k航次t需求量(t)；

Lij——节点i(i∈Δ⋃Ω)至节点j(j∈Δ⋃Ω)距离(n mile)；

Tik——节点i(i∈Δ⋃Ω)燃油k单位装(卸)时间(d)；

Cijv——节点i(i∈Δ⋃Ω)至节点j(j∈Δ⋃Ω)船舶v航行成本(元)；

Cv——船舶v固定成本(元)；

Fik——节点i(i∈Δ⋃Ω)燃油k固定装卸成本(元)；

Cik——节点i(i∈Δ⋃Ω)燃油k单位装卸成本(元·t-1)；

Iik——需求港i燃油k初始库存水平(t)；

Gik——需求港i燃油k单位缺货成本(元·t-1)；

Hik——需求港i燃油k单位库存成本(元·t-1)；

Jik——供应港i供应燃油k时取值为1，需求港i需求燃油k时取值为-1；

Oiv——决策期初船舶v停靠在供应港i时取值为1，否则为0；

δik——供货商在需求港i对燃油k的保守系数。

(3)决策变量

xijtv——0-1 变量，航次t船舶v从节点i(i∈Δ⋃Ω)至j(j∈Δ⋃Ω)时为1，否则为0；

yitv——0-1 变量，航次t船舶v挂靠节点i(i∈Ω)时为1，否则为0；

uiktv——0-1 变量，节点i(i∈Δ⋃Ω)燃油k航次t船舶v配送时为1，否则为0；

ziktvl——0-1变量，节点i(i∈Δ⋃Ω)燃油k航次t船舶v舱室l配送时为1，否则为0；

qiktvl——节点i(i∈Δ⋃Ω)燃油k航次t船舶v舱室l装卸量(t)；

pijktvl——节点i(i∈Δ⋃Ω)至节点j(j∈Δ⋃Ω)燃油k航次t船舶v舱室l装载量(t)。

2.2 模型及转换

由上述问题描述可知，若供货商对需求港i燃油k的保守系数为δik,0 ≤δik≤1，则可设置航次t的累积不确定预算阈值为βikt=δikt[11]，由此得到需求港i燃油k航次t的不确定需求取值集合为

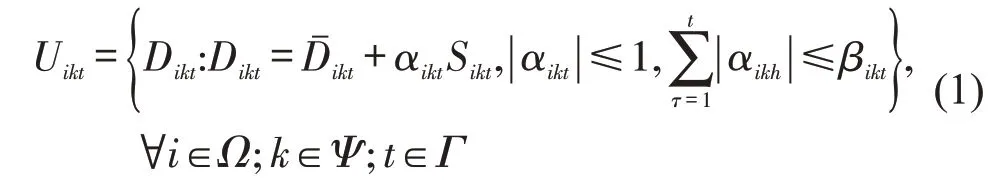
αikt——需求港i燃油k航次t的需求不确定扰动系数；

Sikt——需求港i燃油k航次t需求的最大偏离值(即最大不确定扰动量)。

于是，可构建多品种燃油MIRP 鲁棒优化模型[M1]为

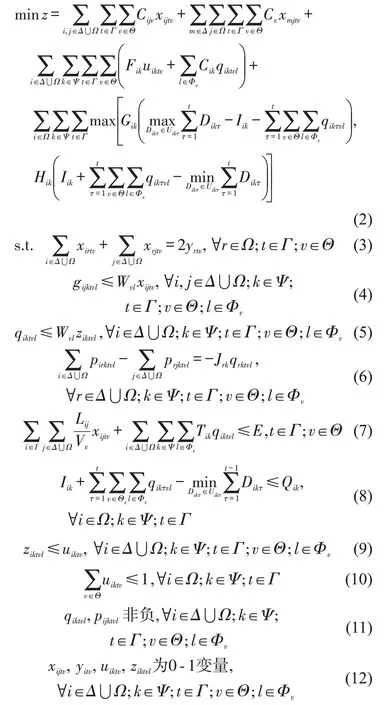
目标函数式(2)表示供货商燃油库存与配送总成本最小化，其中第1项为船舶的航行成本，第2项为船舶的航次固定成本，第3 项为燃油装卸成本，第4项为燃油库存成本或缺货成本，在每一航次t，需求港i燃油k要么缺货，要么不缺货。式(3)表示各航次每艘船挂靠同一需求港最多一次；式(4)和式(5)表示各航次船舶舱室最大装载燃油量限制；式(6)表示船舶路径的流量平衡；式(7)表示船舶完成航次任务；式(8)表示需求港最大库存限制；式(9)和式(10)表示需求港每种燃油每航次最多由一艘船舶配送；式(11)和式(12)表示变量约束。

由于模型[M1]的目标函数式(2)和约束式(8)中均含有非线性结构，且含有需求不确定性(随机)变量Dikt(i∈Ω,k∈Ψ,t∈Γ)，不能直接求解。为此，本文借鉴文献[12]对其进行线性转化。引入对偶变量ηikt和θikτt以及辅助变量bikt，当供货商给定需求港i燃油k的保守系数δik，即航次t不确定预算参数值βikt已知时，将模型[M1]转换为线性模型[M2]，即

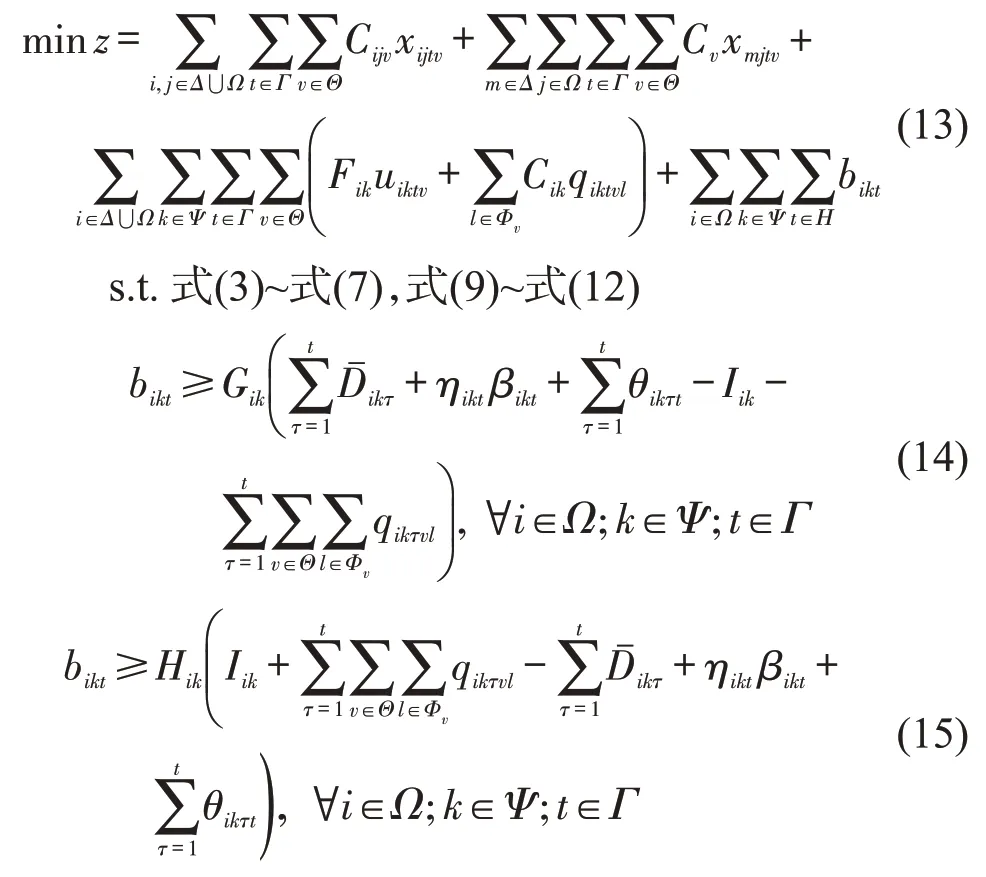
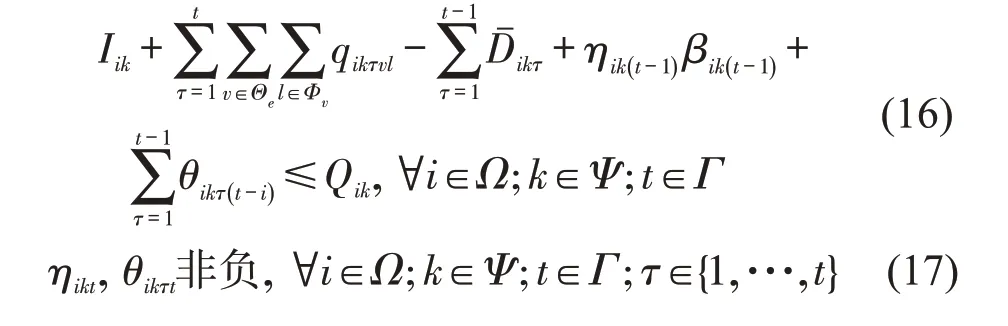
3 算法设计

本文研究的多品种燃油MIRP 属于NP 难问题IRP的一个变种[13]，该问题包含各品种燃油供/需港匹配、船舶路由指派和舱室配载等3项主要决策内容。遗传算法是求解MIRP 决策的一种有效算法[14]，适用性较强，能够有效求得不同模型参数下的解，但在本文的MIRP中，由于存在多供/需港、多品种燃油、多航次、多类型船舶和多舱室的复杂匹配组合，染色体编码过长会导致算法搜索效率过低。为此，本文依据AGA具有收敛速度快、避免早熟现象，以及ALNS算法具有快速随机搜索能力，适用于大规模路由指派问题求解的特征，将ALNS算法和Gurobi 求解器嵌入AGA 中，设计改进HAGA 求解模型[M2]。算法总体框架如图2所示。

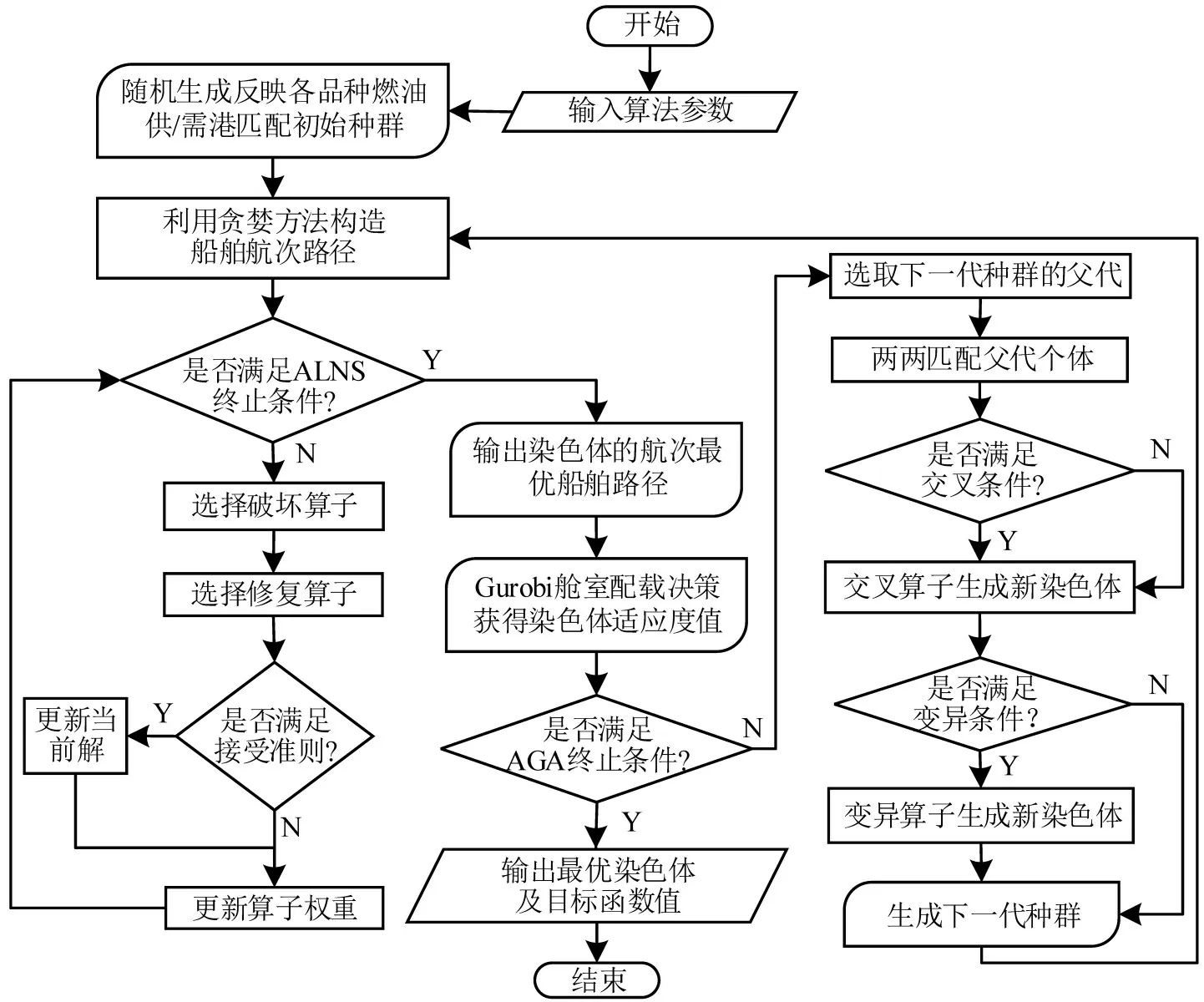
图2 改进HAGA流程Fig.2 Flow of improved HAGA

由图2可知，改进HAGA求解的核心可拆分成3 部分：一是将各供/需港各品种燃油进行聚类，以二进制编码方式随机生成反映各品种燃油供/需港匹配的初始种群或经交叉变异生成的下一代种群；二是根据生成初始种群中的染色体信息，以船舶航次配送成本最小化为目标，设计ALNS 算法，获取航次船舶路径；三是以供货商燃油库存与配送总成本最小为目标，调用Gurobi求解器计算得出航次船舶各舱室配载和需求港配送量决策。改进HAGA算法求解步骤如下。

Step 1 设置改进HAGA最大进化代数、交叉和变异概率等参数。

Step 2 染色体编码和种群初始化。采用二进制编码方式随机生成染色体，将具有相同供/需港口的燃油归为一类。当某航次某需求港某品种燃油所对应染色体的基因值为1时，则表示在此航次要安排船舶挂靠该需求港，并对该品种燃油进行补货；否则，不补货。据此随机生成一个规模为R的反映船舶挂靠需求港情况的初始化种群。

Step 3 航次船舶路径指派。根据种群中染色体信息，嵌套设计ALNS算法，获取航次船舶路径。

Step 4 计算适应度值。将适应度函数设为模型[M2]目标函数的倒数。显然，染色体适应度值越高，对应的解就越好。在最优航次船舶路径下，以供货商燃油库存与配送总成本最小为目标，调用Gurobi 求解得到船舶各舱室最优燃油配载和各需求港配送量决策，将总成本的倒数作为染色体的适应度值。

Step 5 选择算子。采用精英保留和轮盘赌相结合的策略，将最优染色体直接作为下一代种群的父代。

Step 6 交叉算子。采取动态调整交叉概率的自适应策略，在染色体适应度值进行由大到小排序的基础上，将父代染色体进行两两匹配，对满足交叉条件的两个父代进行交叉操作。

Step 7 变异算子。采取动态调整变异概率的自适应策略，随机选择满足变异条件染色体的两个基因位置，翻转其基因值。

Step 8 计算新产生染色体的适应度值。重复Step 3 和Step 4，得到所有新产生染色体的适应度值。

Step 9 改进HAGA 终止准则。若进化到最大代数，则输出最优解；否则返回Step 5。

4 算例分析

4.1 数据选取与算例计算

为验证改进HAGA 解决模型[M2]的适用性和有效性，本文生成两组小规模的两种燃油海运供应问题的测试算例，记为测试问题1(TP1)和测试问题2(TP2)，与文献[15]中求解确定型需求同类研究问题的遗传算法和Cplex 精确算法进行对比。其中，TP1含有1个供应港和4个需求港，TP2含有1个供应港和5 个需求港。船舶完成一个航次燃油配送任务在5 d以内，决策期为10 d，共两个航次。假设供货商风险中性，即供货商在各港口的两种燃油保守系数取值均为0.5。供货商拥有2艘船舶，净载重量分别为1500 t 和3000 t，航速分别为11.0 kn 和12.5 kn，隔离油舱均为2个。港口装卸固定成本为1000 元·艘次-1，单位装卸成本为1 元·t-1，两种燃油的单位缺货成本分别为10元·t-1·d-1和11元·t-1·d-1，单位库存成本分别为2.5 元·t-1·d-1和2.3 元·t-1·d-1。各航次各港口各品种燃油需求最大偏离值为其均值的25%，期初库存和需求均值如表1所示。

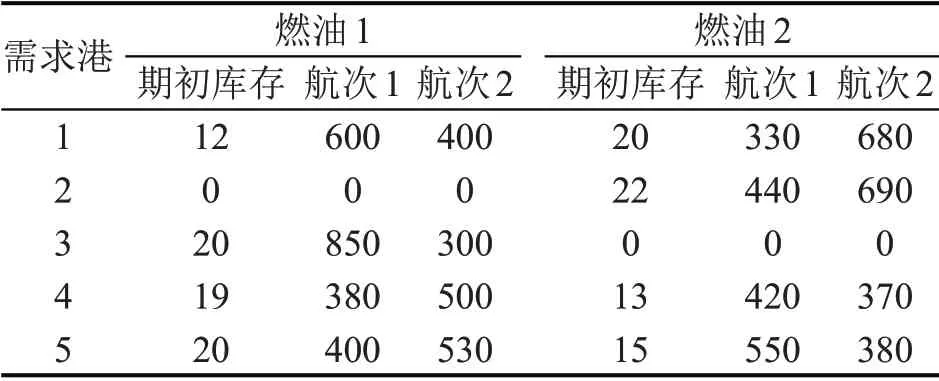
表1 期初库存和需求均值Table 1 Initial inventory and average demand(t)

设置改进HAGA 主要参数如下：种群规模为30，最大进化代数为50，最小交叉概率为0.1，最小变异概率为0.01，k1、k2、k3、k4取值依次为0.8、0.4、0.09、0.1，ALNS算法最大迭代次数为100，λ取值为0.5，ω1、ω2、ω3、ω4取值依次为1.5、1.2、0.8、0.6。

本算例使用Python3.8 编程，在CPU 为i5-10210U、内存为16 GB的电脑上进行测试。本文改进HAGA(算法1)与文献[15]的多启发式遗传算法(算法2)和Cplex 精确算法(算法3)的计算结果如表2所示。

由表2 可知，算例TP1 和TP2 中，在运行时间、解的平均值和最优值方面，算法1均优于算法2；在解的最优值方面，采用算法1 与算法3 得到的两个算例结果分别仅相差1.17%和3.55%。在算例TP2的运行时间方面，算法3 远远大于算法1 的运行时间。实验结果表明，改进HAGA 求解多品种燃油MIRP有效。

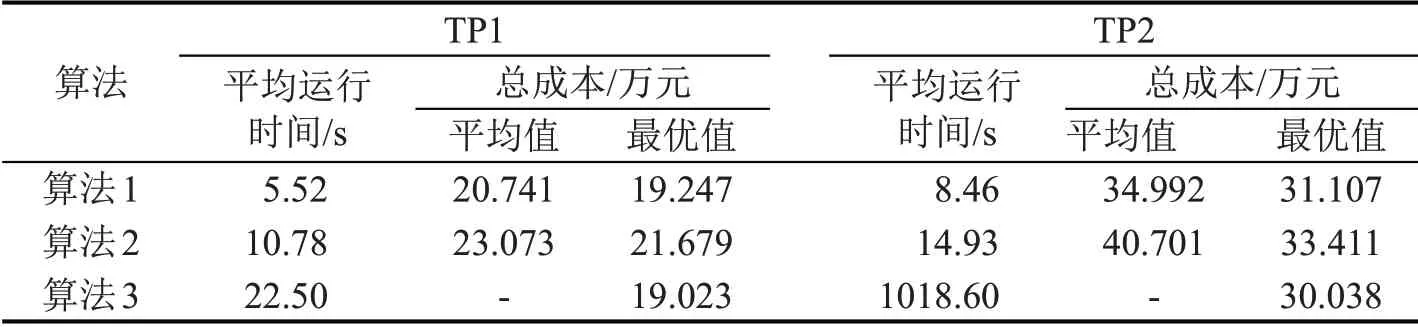
表2 不同算法计算结果Table 2 Computing results with different algorithms

为了求解实际中的多品种燃油MIRP，本文以天津港和大连港作为两个供应港，向环渤海区域8个需求港配送4 种燃油(图1)为例，记为问题3(TP3)。各港口间的距离数据取自航运在线网站，船舶完成一个航次燃油配送任务在10 d以内，考虑到需求的不确定性，供货商的决策期设为1 个月，则决策期可等分为3 个航次。供货商拥有净重量分别为1500 t 和3000 t，隔离油舱分别8 个和10 个的两类船舶各两艘，船舶其他参数同TP1。4 种燃油的单位缺货成本分别为10，11，12.5，10元·t-1·d-1，单位库存成本分别为2.5，2.3，1.9，3 元·t-1·d-1。供货商保守系数、需求最大偏离值等参数同TP1，各航次各港口各品种燃油的期初库存和需求均值如表3所示。

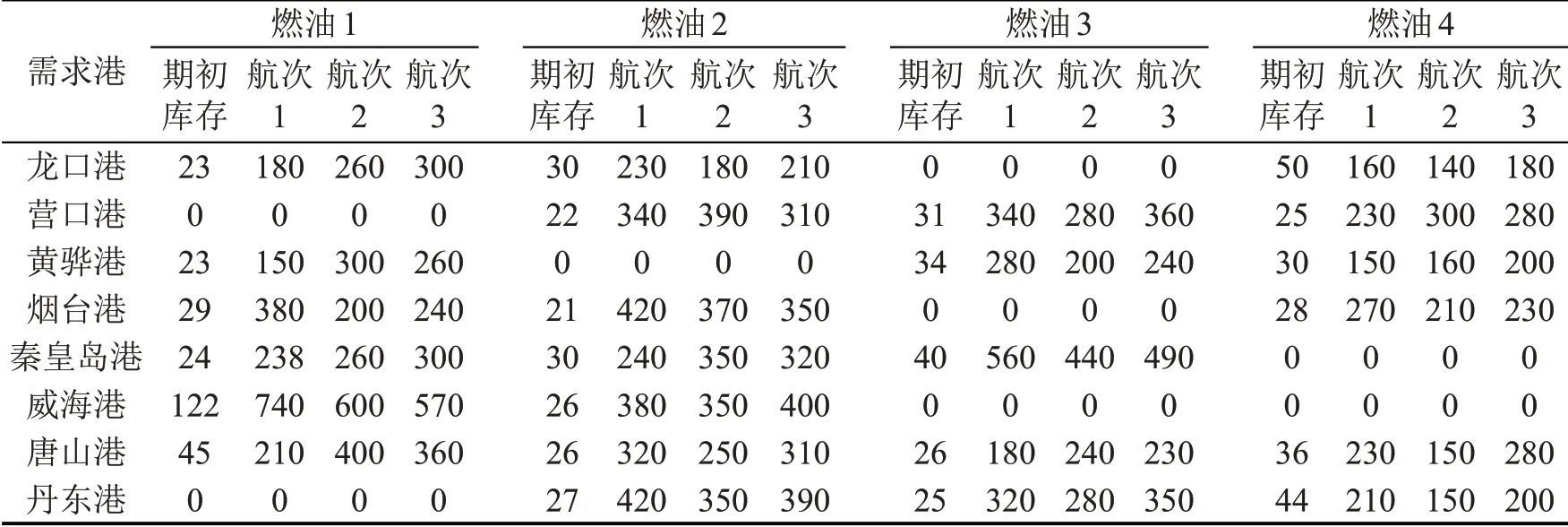
表3 期初库存和需求均值Table 3 Initial inventory and average demand(t)

将ALNS 最大迭代次数设为500，其他算法参数同上。采用本文提出的非专用舱室和船舶非固定停靠港配送模型及算法(模型&算法1)、本文模型及运行86400 s的Cplex近似解(模型&算法2)，以及文献[8]专用舱室和船舶固定停靠港配送模型及本文算法(模型&算法3)，对算例TP3 求解，得到计算结果对比如表4所示。

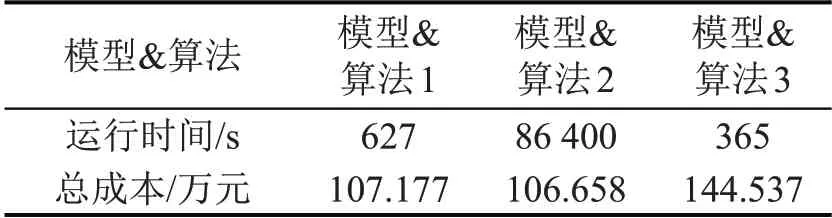
表4 计算结果对比Table 4 Comparison of computing results

由表4 可知，模型&算法1 得到的供货商燃油库存与配送总成本与模型&算法3 仅相差0.48%，比模型&算法2 的结果节约了25.85%。在运行时间方面，模型&算法1 与模型&算法3 相比，具有明显的优势。究其原因，是由于本文模型采取非专用舱室和非固定停靠供应港策略的多品种燃油联合配送，既能提高船舶利用率，减少挂靠成本和缺货成本，又能将各需求港各品种燃油的库存决策与船舶配送路径决策有机地加以集成，增加库存与配送路径方案的灵活性，从而有效降低供货商燃油库存与配送总成本。结果表明，本文设计的改进HAGA能有效解决实际需求不确定情形下的多品种燃油MIRP。

4.2 敏感性分析

为了帮助供货商实际决策时所选保守水平的供应方案能达到供货商预期的客户服务水平，故在假设燃油需求服从正态分布的情景下，分析供货商保守水平在[0.1,0.9]区间范围内取值变化时，对各需求港各品种燃油客户服务水平的影响，结果如图3所示。

从图3 可知，随着供货商保守系数的增大，供货商对于各需求港各品种燃油的客户服务水平均随之增大。虽然其增大变化趋势不尽相同。但当供货商设置的各需求港各品种燃油保守系数超过其各自的某一恰当(right)值时，对应的客户服务水平变化就趋于平缓。如图3(a)中，当供货商设置的龙口港燃油1 保守系数超过恰当值0.6 时，客户服务水平变化趋于平缓；在图3(g)中，当供货商设置的唐山港燃油3 保守系数超过恰当值0.5 时，客户服务水平变化亦趋于平缓。此外，供货商保守水平变化对供货商燃油库存与配送总成本影响的敏感性分析结果如表5所示。

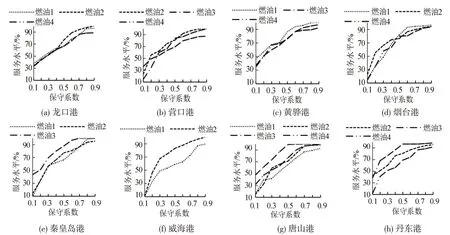
图3 供货商保守系数对客户服务水平的影响Fig.3 Influence of supplier's conservative coefficient on customer service level

表5 总成本随保守系数的变化Table 5 Variation of total cost over conservative coefficient

由表5 可以看出，随着保守系数的增大，供货商燃油库存与配送总成本近似呈线性增大。究其原因，是因为随着保守系数的增大，供货商需要在各需求港保有更多的燃油库存，使得供货商燃油库存与配送总成本都随之增大。结合图2可知，在某需求港某品种燃油供货商保守系数取值超过其恰当值时，客户服务水平不再有明显的变化，而供货商燃油库存与配送总成本仍会明显增加。因此，供货商可以根据实际情况，选择合适的各需求港各品种燃油保守系数取值范围，以实现既满足客户服务水平要求，又降低供货商燃油库存与配送总成本的目标。

5 结论

在不确定需求情形下的多品种燃油MIRP 中，库存管理、船舶路由指派、舱室配载等问题相互影响和制约，能否有效解决这一难题是供货商控制成本、提升竞争力的关键。本文基于非专用舱室和非固定停靠供应港策略，建立的多品种燃油MIRP 鲁棒优化模型，设计了一种改进HAGA 求解算法，通过不同规模的算例分析，验证了模型和算法的适用性和有效性。研究得到以下结论：

(1)多品种燃油的非专用舱室和船舶非固定停靠港配送可提高船舶舱室利用率，增加库存和配送路径方案的灵活性，降低供货商燃油库存与配送总成本；

(2)供货商保守系数与客户服务水平以及供货商总成本均呈正相关关系，且供货商在需求港关于各品种燃油均存在不同的保守系数恰当值，当供货商各需求港各品种燃油保守系数超过该恰当值时，客户服务水平变化就趋于平缓。

本研究的管理启示如下：①在海运供应链VMI模式下，供货商可结合燃油配送船舶拥有多个舱室的特征，根据各需求港各品种燃油的库存和需求信息，采取非专用舱室策略，合理地进行船舶舱室燃油配载决策，并灵活地安排完成航次配送任务的船舶在就近供应港停靠，以实现多需求港多品种燃油的库存与配送优化；②在各港口各品种燃油需求不确定的情形下，供货商应积极开展燃油需求的调研和预测工作，及时获取决策期各航次的燃油需求均值等信息，即使因燃油需求概率分布难以获得而导致无法确定各需求港各品种燃油供货商保守系数的恰当值，供货商仍需要结合实际预设适当的客户服务水平目标，在合适的取值范围内设置各需求港各品种燃油供货商保守系数，以防供货商保守系数设置过大而出现燃油库存与配送总成本剧增的不利局面。