考虑匹配优先级的共享混合停车位租用与分配问题研究

李常敏，魏文彬，张露

(上海大学，管理学院，上海 200444)

0 引言

随着节能环保、价优的新能源车普及，当前配建充电桩的混合停车场日益增多。然而，由于车与位数量的严重失衡导致大量燃油车占用充电车位，充电需求用户需要参与到寻找车位的无效交通流中，增加城市交通负担。针对燃油车“鸠占鹊巢”的问题，政府出台了新版《电动汽车充电站运营管理规范》来治理停车乱的现象，其中明确规定“燃油车不得影响充电车位的正常使用”。当下车位供需不平衡问题使得政策难以在短时间内发挥作用，错峰错时进行车位共享被认为是有效缓解城市停车供需矛盾的重要途径之一[1]。

关于共享停车的研究主要集中在基于车位供给量确定下的分配策略和考虑车位供需双方随机性的分配策略这两个方向。在车位供给量确定的前提下，姚恩建等[2]针对提高泊位利用率的问题，以停车需求时段和车位空闲时段无冲突为约束条件建立共享车位资源优化配置模型。考虑到停车后驾驶员的步行距离，张文会等[3]建立共享停车泊位利用率最大化和步行距离最小化的双目标泊位分配模型，并设计粒子群多目标搜索算法对模型进行求解。Li等[4]针对出行者在使用共享车位时存在违约的可能性，建立考虑出行者信用风险的共享停车位优化模型，通过改进的蚁群算法对模型进行求解，验证了模型的有效性。在供需不确定的前提下，Jiang等[5]建立了出行者和车位拥有者在不同时段的停车概率函数及车位分配模型，研究发现，预留的最佳空闲停车位数与不准时率和相邻时隙登记到达和离开的车辆数有关。Shao 等[6]认为共享平台拒绝停车请求带来的潜在损失不能被忽视，建立考虑停车泊位供需时间冲突特征和拒绝停车请求带来损失的车位分配模型。在此基础上，孙会君等[7]考虑平台拒绝车位供给用户所带来的潜在损失问题，构建共享车位租用与分配模型。为提高共享停车平台的服务水平和收益，路扬等[8]基于共享平台系统中不同使用频率的用户设置了优先级系数，建立了考虑优先级的网络共享停车匹配优化模型。

混合泊位停车场能在一定程度上缓解新能源车充电难的问题，但由于缺乏良好的供需匹配模式，易引发充电和停车需求间的冲突问题，而这个冲突问题是普通停车场不具备的。基于此，本文以混合泊位停车场为研究对象，从车位停车资源和充电资源合理利用的角度出发，建立考虑匹配优先级的车位租用与分配集成决策的整数规划模型。为简化问题，将模型转化为加权顶点图着色问题，并结合匹配优先级及冲突矩阵的特殊性提前选出优先级高的顶点作为优先着色点，减少可着颜色的数量。继而，改进蚁群算法对模型进行求解。

1 考虑匹配优先级的共享混合停车位租用与分配模型

1.1 问题描述

考虑一个负责车位租用和分配的共享车位平台，假设平台共接收到|N|个普通车位和|M|个充电车位提供的出租信息，每个普通车位n，n∈N，空闲时间窗[tn,start,tn,end]，时长tn,dur=tn,end-tn,start，其中，tn,start和tn,end分别表示普通车位闲置的起始和终止时间；每个充电车位m，m∈M，空闲时间窗[tm,start,tm,end]，时长tm,dur=tm,end-tm,start，其中，tm,start和tm,end分别表示充电车位闲置的起始和终止时间。平台共接受|I|个普通停车需求，每个停车需求i，i∈I，停车时间窗[ti,start,ti,end]，时长ti,dur=ti,end-ti,start，其中，ti,start和ti,end分别表示普通停车需求用户停车的起始和终止时间；共接受了|H|个充电和停车的复合需求，每个复合需求h，h∈H，充电需求量已知Qh，停车时间窗[th,start,th,end]，时长th,dur=th,end-th,start，其中，th,start和th,end分别表示复合需求用户停车的起始和终止时间，充电时长包含在停车时长内。

平台若能将普通停车位分配给停车需求，则平台会租用该车位，付给车位供给方租金，单位时长租金C1，从停车需求方收取停车费，单位时长停车费P1。若不能分配，则平台不接单，即会拒绝供给方或需求方，但会因为拒绝供给方造成潜在损失，单位时长损失θ，拒绝需求方造成的潜在损失，单位时长损失τ。平台若能将充电停车位分配给普通停车需求或充电停车复合需求，则平台会租用该车位，付给车位供给方租金，单位时长租金C2，C2＞C1，从充电停车复合需求方获得停车费或充电费，单位时长停车费P1，单位时长充电费P2；从普通停车需求方获得停车费，单位时间停车费P3，P3＞P1。若不能分配，则平台不接单，即会拒绝供给方或需求方，但会因为拒绝供给方造成潜在损失，单位时长损失γ，拒绝普通停车需求方造成潜在损失，单位时长损失τ，因拒绝复合需求方造成潜在损失，单位时长损失β。

由于停车场乱停现象时有发生，导致充电需求无法被满足，充电车位资源难以得到最大程度地利用。平台将会为不同的分配方式设定不同的优先级：复合需求与充电车位的匹配方式D1能为平台带来停车收益以及充电收益，优先级最高；停车需求与普通车位的匹配方式D2在满足停车需求的同时，不占用其他充电停车位资源，优先级次高；停车需求与充电车位的匹配方式D3的优先级最低，这是因为停车需求只停车，在占用充电车位后会浪费充电资源，还会影响后续充电用户的充电需求。这3种匹配方式的优先级为

1.2 模型建立

对预约用户、充电车位以及价格分别作如下基本假设：

假设1 预约用户不会因为自身情况，临时取消预约和拒绝平台分配结果。每个预约用户准确知道所需的停车时长和需求电量。充电需求用户的充电时间包含在其停车时间内。

假设2 充电车位的充电桩为可变功率充电桩，且整个停车场有功率限制，超过限制会影响充电效率。

假设3 平台租用停车位的价格满足C2＞C1，收取停车费的价格满足P3＞P1，充电价格P2不受充电高峰期和低谷期影响，惩罚系数满足。β ＞τ,γ ＞θ

引入如下决策变量：

xin为停车请求i是否被分配到普通车位n，若将其分配，xin=1，否则xin=0，其中i∈I,n∈N；

xim为停车请求i是否被分配到充电车位m，若将其分配，xim=1，否则xim=0，其中i∈I,m∈M；

xhm为复合请求h是否被分配到充电车位m，若将其分配，xhm=1，否则xhm=0，其中h∈H,m∈M；

yn为平台是否租用普通停车位n，若租用，yn=1，否则yn=0，其中n∈N；

ym为平台是否租用充电车位m，若租用，ym=1，否则ym=0，其中m∈M。

基于以上分析，建立考虑匹配优先级的共享车位租用和分配(MPRA)模型的运营商利润最大化目标函数为

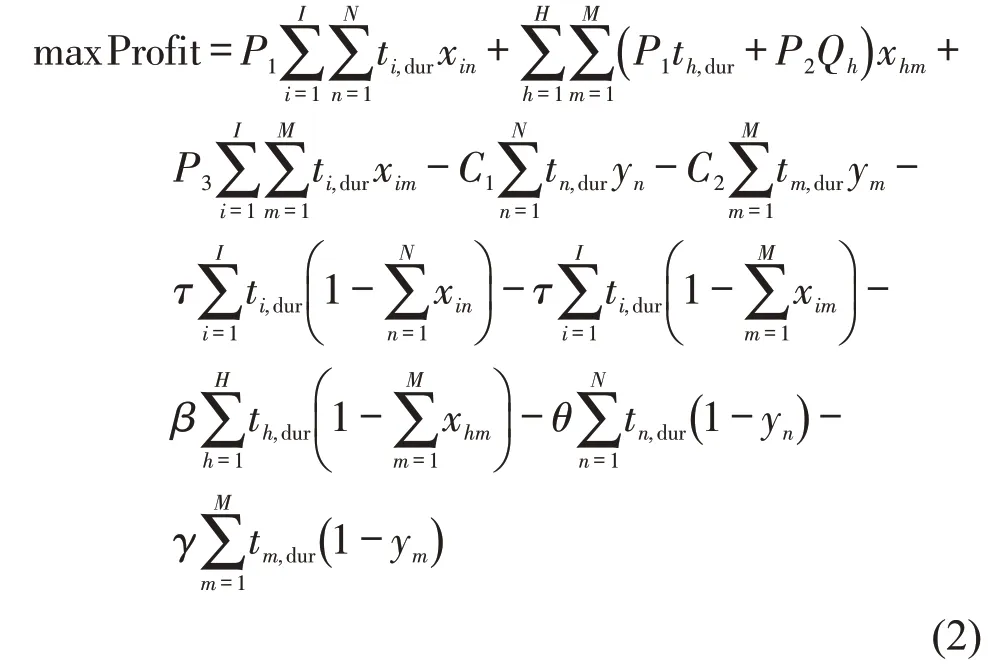
式(2)第1 项表示平台接受停车请求带来的收益，第2项表示平台接受充电请求带来的收益，第3项表示平台接受停车预约用户停入充电车位所带来的收益，第4项表示租用普通停车位的成本，第5项表示租用充电车位的成本，第6～第8项表示拒绝复合请求给平台带来的潜在损失，第9和第10项分别表示拒绝租用普通车位和充电车位给平台带来的潜在损失。

车位在分配过程中的约束条件如下。

任意停车请求i最多被分配至一个普通停车位，即

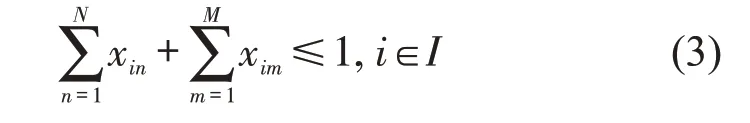
任意充电请求h最多被分配至一个充电车位，即

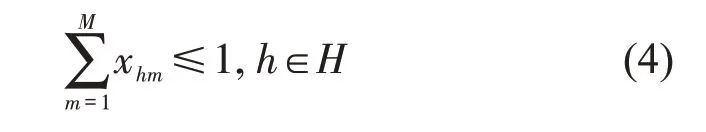
被分配至同一车位的请求，应不存在停车时间冲突，即

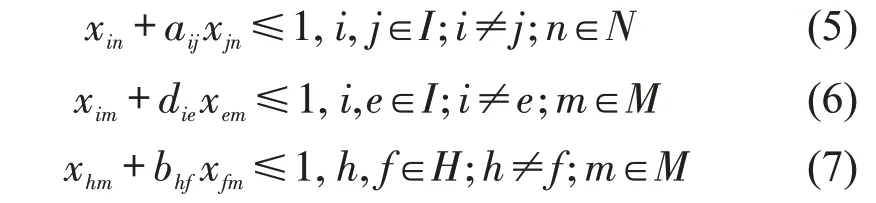
式中：aij=1 表示停车需求i与j分配至普通车位时预约时段不存在冲突，否则，aij=0；die=1 表示停车需求i与e(i,e∈I,i≠e)分配至充电车位时预约时间段不存在冲突，否则，die=0；bhf=1 表示复合需求h与f(h,f∈H,h≠f)分配至充电车位时预约时间段不存在冲突，否则，bhf=0。

若停车或充电请求被分配至车位，则请求需满足该车位的时间窗约束，即

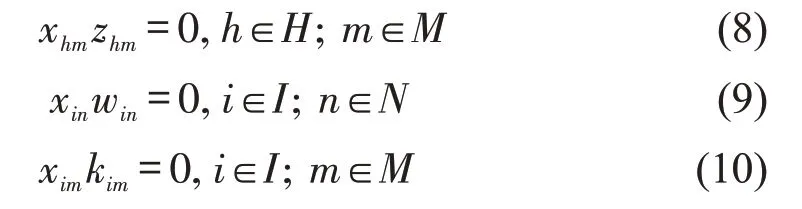
式中：win=1 表示停车需求i的停车时段超过普通停车位n的共享时段，否则，win=0；kim=1 表示停车需求i的停车时段超过充电车位m的共享时段，否则，kim=0；zhm=1 表示复合需求h的停车时段超过充电车位m的共享时段，否则，zhm=0。

所有被分配在同一个车位的请求所占用时长不应超过该车位的共享时长，即

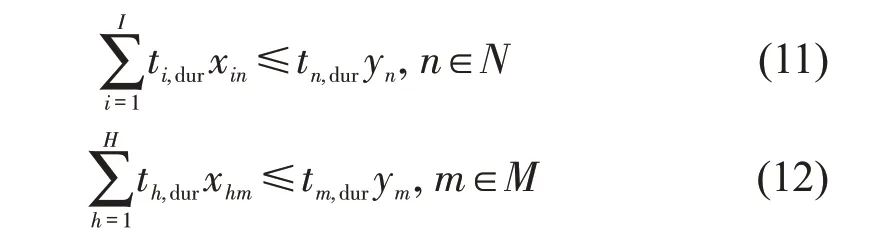
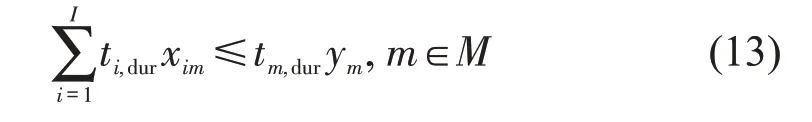
停车场内所有电动汽车所占用的充电功率不超过停车场的总功率Pp-pow，即

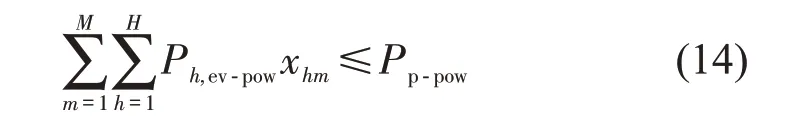
式中：Ph,ev-pow为第h个充电停车复合需求用户的充电功率。

在充电停车复合需求用户的停车时长内，充电车位能够给复合需求用户提供的电量不小于其需求电量Qh，即

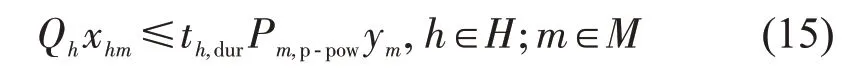
式中：Pm,p-pow为第m个充电车位的充电功率。

2 求解算法

图着色问题通过对图结构中的顶点赋予一组唯一的颜色值，并且满足存在边连接的两个顶点对应不同颜色值。借助这一原理，本文以停车需求集和复合需求集作为顶点集，每个顶点赋值为相应需求的停车时长或充电时长，以普通车位集和充电车位集构成颜色集，通过冲突矩阵构建边集，即对存在需求时段冲突的顶点用边连接，进而将模型转化为具有颜色约束的加权顶点图着色问题[2]。在此基础上，借鉴蚁群算法对模型进行求解。

为保证每只蚂蚁在寻找路径时优先满足复合需求，将顶点按照复合需求和停车需求进行排序，并对供需冲突矩阵进行分块。如图1所示，阴影表示存在时间冲突，第I部分表示复合需求集H与充电车位集M之间的冲突关系，第II 部分斜线格表示所有复合需求H无法停入普通车位N中，第III部分表示停车需求I与普通停车位N之间的冲突关系，第IV 部分表示停车需求I与充电车位M之间的冲突关系。对冲突矩阵分块将大大节省算法的搜索时间，这是由于蚁群算法给顶点着色过程中，需要从整个颜色集合中选择颜色，并试探其与该顶点是否存在冲突，而第II部分尽可能地缩小了颜色选择的范围。

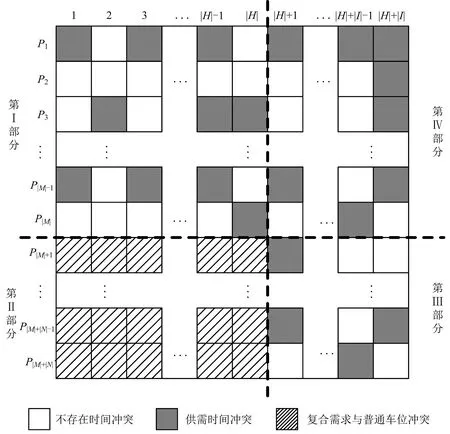
图1 分块供需冲突矩阵Fig.1 Block conflict matrix about supply and demand

基于上述分析，算法步骤描述如下：

Step 1 设置初始参数值。包括停车和充电供需双方的信息，蚁群算法相关参数，信息素浓度下限τmin。令初始迭代次数CNC=0，转Step 2。

Step 2 根据匹配优先级的设定，K只蚂蚁着色路径的起点与复合需求H相关，因此优先筛选出H并生成随机数，确定蚂蚁放置的起点，转Step 3。

Step 3 更新全局信息素表。根据分块冲突矩阵对蚂蚁k在遍历过程中释放的信息素进行分段，即

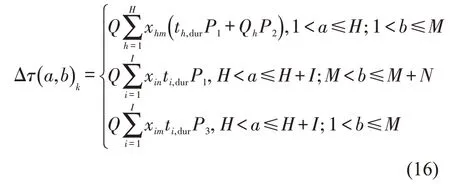
式中：Q为信息素更新参数。根据信息素更新方程和式(16)计算信息素浓度。若信息素浓度小于τmin，令信息素浓度等于τmin，否则直接更新，转Step 4。

Step 4 根据分块冲突矩阵、式(14)和式(15)判断可选颜色集合并着色。若为空集，蚂蚁无法完成对该顶点着色，即无法完成匹配；否则，每只蚂蚁根据转移规则和式(17)选择给该顶点分配的颜色，其中蚂蚁将车位b分配给a的期望程度ηab设置为成本率的倒数，即

完成所有顶点的着色，转Step 5。

Step 5 记录历史最佳方案，转Step 6。

Step 6 检查是否达到最大迭代数CNCmax，若达到，转Step 7；否则，令CNC=CNC+1，转Step 2。

Step 7 输出最优分配方案。

3 仿真实验

为验证本文所提模型及算法的有效性和合理性，根据居住区共享车位的空闲特性设计仿真实验。假设平台共收到12 个停车需求和5 个车位出租信息，其中2 个充电车位，可租用时段如表1所示。

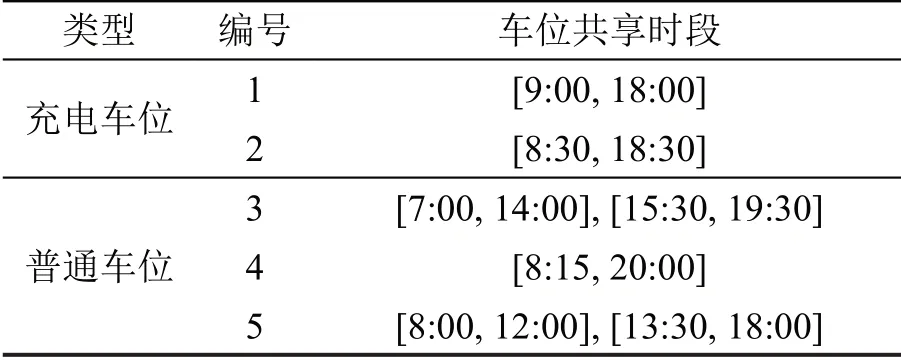
表1 出租时段信息Table 1 Rental time information

12 个停车需求中包含2 个复合需求和10 个普通停车需求，具体的需求时段如表2所示。

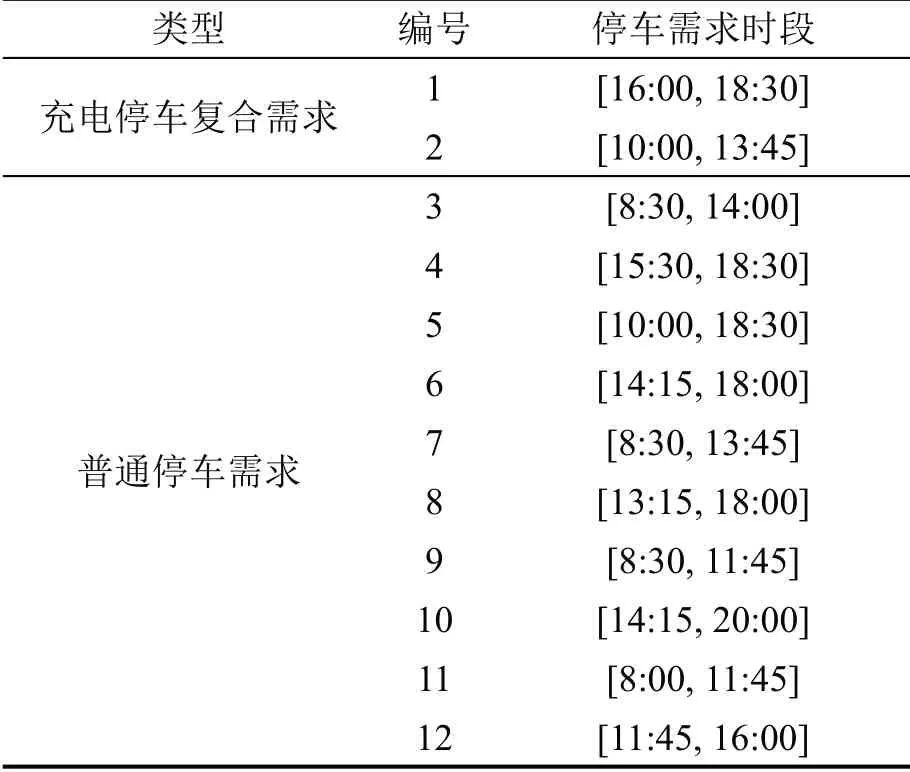
表2 停车需求时段信息Table 2 Parking demand time information

参照1995年发布的《上海市收费停车场(库)计费规定》的标准，对一些初始参数进行设置，其中两个充电用户需求电量分别为60 度和50 度，停车和充电单价分别是P1=10元·h-1,P3=15元·h-1,P2=0.8元·kWh-1，租用车位成本是C1=5元·h-1,C2=8元·h-1，若拒绝则惩罚成本为τ=0.5 元·h-1,β=0.6 元·h-1,θ=0.4 元·h-1,γ=0.5 元·h-1。取蚂蚁数K=6，最大迭代次数CNCmax=5000，信息素和启发式重要程度因子分别为ψ=3,φ=9,信息素蒸发系数ρ=0.35，信息素更新参数Q=10。

不考虑匹配优先级(NMP)情形下，分配结果如图2所示，图中除阴影部分外表示车位可出租时段，而空白方格代表各停车需求时段。

在NMP 情况下，平台运营商在进行匹配时往往忽略了停车资源的合理利用，根据图2显示的分配结果，2号充电需求无法被满足，这是因为2号的需求时段与12 号停车需求以及8 号停车需求存在冲突，平台选择将车位分配给收益更高的普通停车需求用户。这显然不符合当前我国的《电动汽车充电站运营管理规范》政策。为防止燃油车占用充电车位而影响充电需求，利用本文所提算法，计算结果如图3所示。

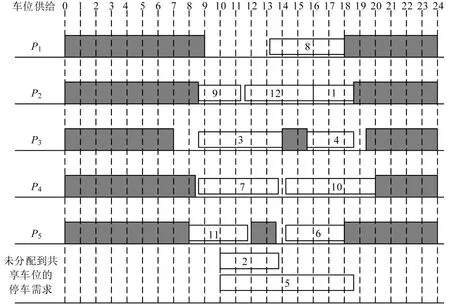
图2 NMP分配方案Fig.2 NMP allocation scheme

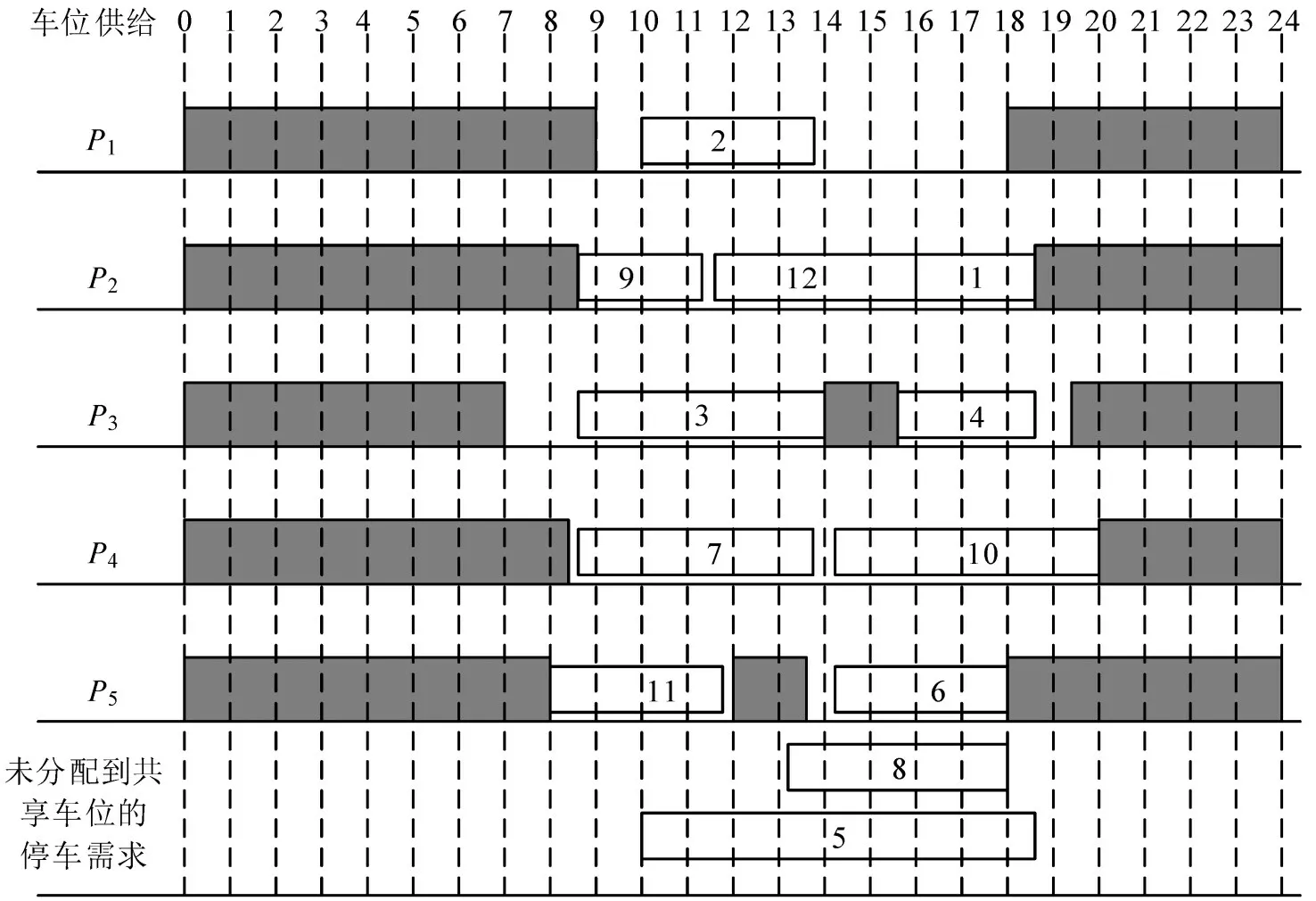
图3 MPRA分配方案Fig.3 MPRA allocation scheme

对比图2 和图3 的分配方案可知，在未考虑匹配优先级情形下，出于运营商利润最大化的角度，充电车位1 被停车需求8 所占用，无法使用充电车位，而在考虑匹配优先级的情况下，车位资源得到了合理利用，充电需求1 和2 都被满足。为揭示本文所提模型和算法下充电需求优先被满足产生的原因，图4 给出更直观的租用和分配方案。由图4可知，由于存在左下角的斜线阴影区域，这使得供需冲突矩阵进行分块处理，充电需求会被优先满足，并且颜色集合元素数量减少。

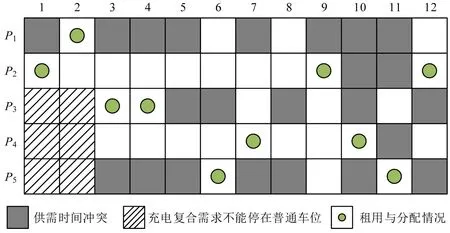
图4 租用与分配方案Fig.4 Rental and allocation scheme

为验证算例规模对MPRA方案的影响，分别对停车位数量和出行者数量设置4 种不同的测试规模，并与先到先停(FCFS)方案进行比较，结果如表3所示。

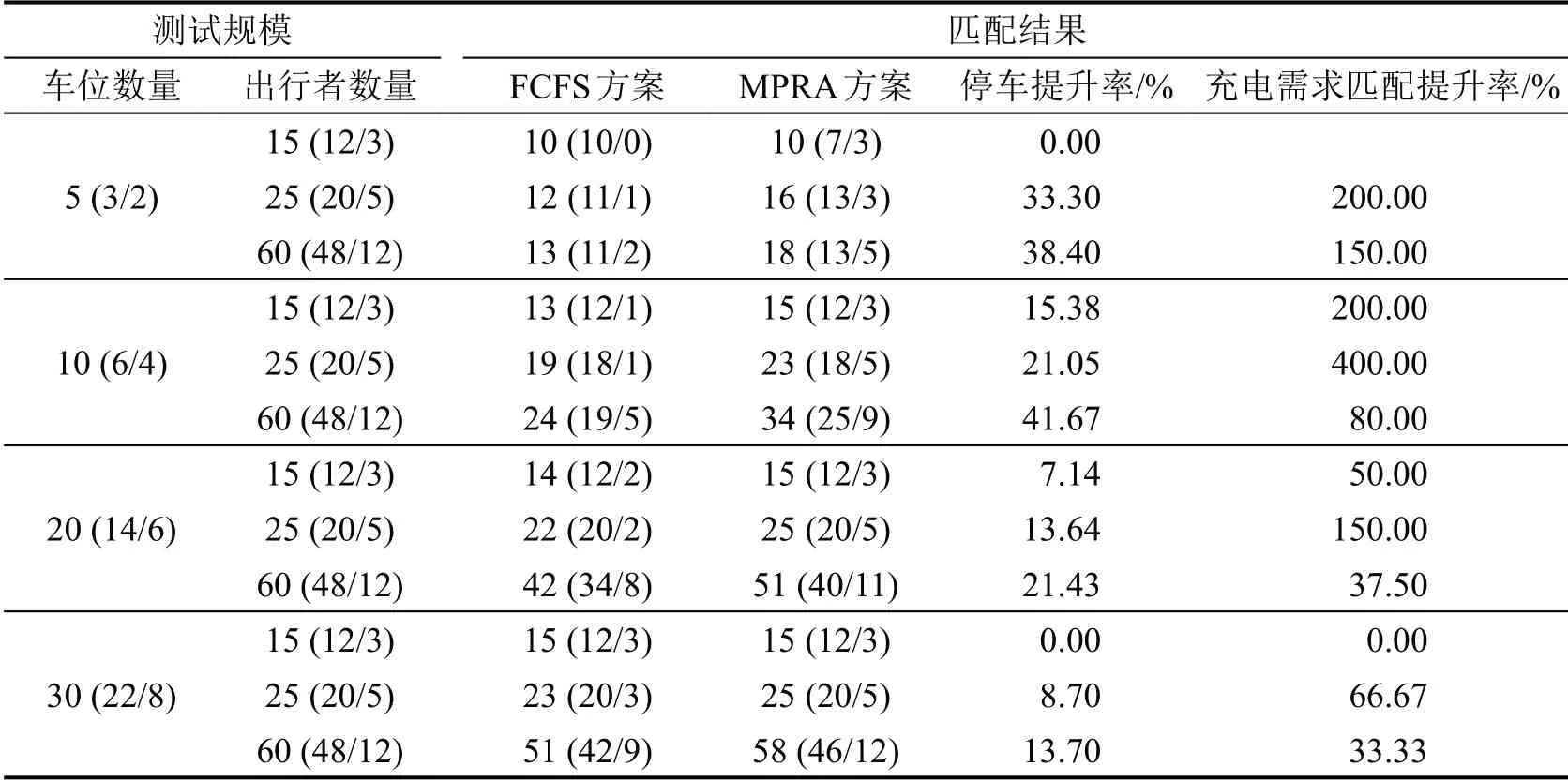
表3 FCFS方案与MPRA方案在不同规模下的比较结果Table 3 Comparison results of FCFS and MPRA at different scales

由表3 可知，当出行者数量不变时，随着车位数量的增加，MPRA方案下停车提升率和充电需求匹配提升率相对FCFS 方案的优势逐渐减弱。然而，当停车位数量不变时，随着出行者数量的增加，MPRA 方案下停车提升率和充电需求匹配提升率相对FCFS方案的优势明显。停车平均提升率和充电需求匹配平均提升率分别为17.87% 和113.96%。因此，在针对混合停车场共享车位数量有限时，平台采用MPRA方案可优化混合泊位停车场的车位利用率，且在满足更多需求的同时能合理利用车位的停车资源和充电资源。进一步比较不同规模下的MPRA 方案与NMP 方案，结果如表4所示。

根据表4 可以看出，相对NMP 方案，当出行者数量或停车位数量单方面增加时，MPRA方案下停车提升率和充电需求匹配提升率的优势逐渐减弱，但充电需求匹配平均提升率仍达到28.96%，且收益提升率优势逐渐突出，平均提升1.34%。因此，在出行者数量稳定时，平台可以考虑增加租用车位数量来提高平台的收益；而共享车位数量较为稳定时，考虑接收更多的需求来提高平台的收益。

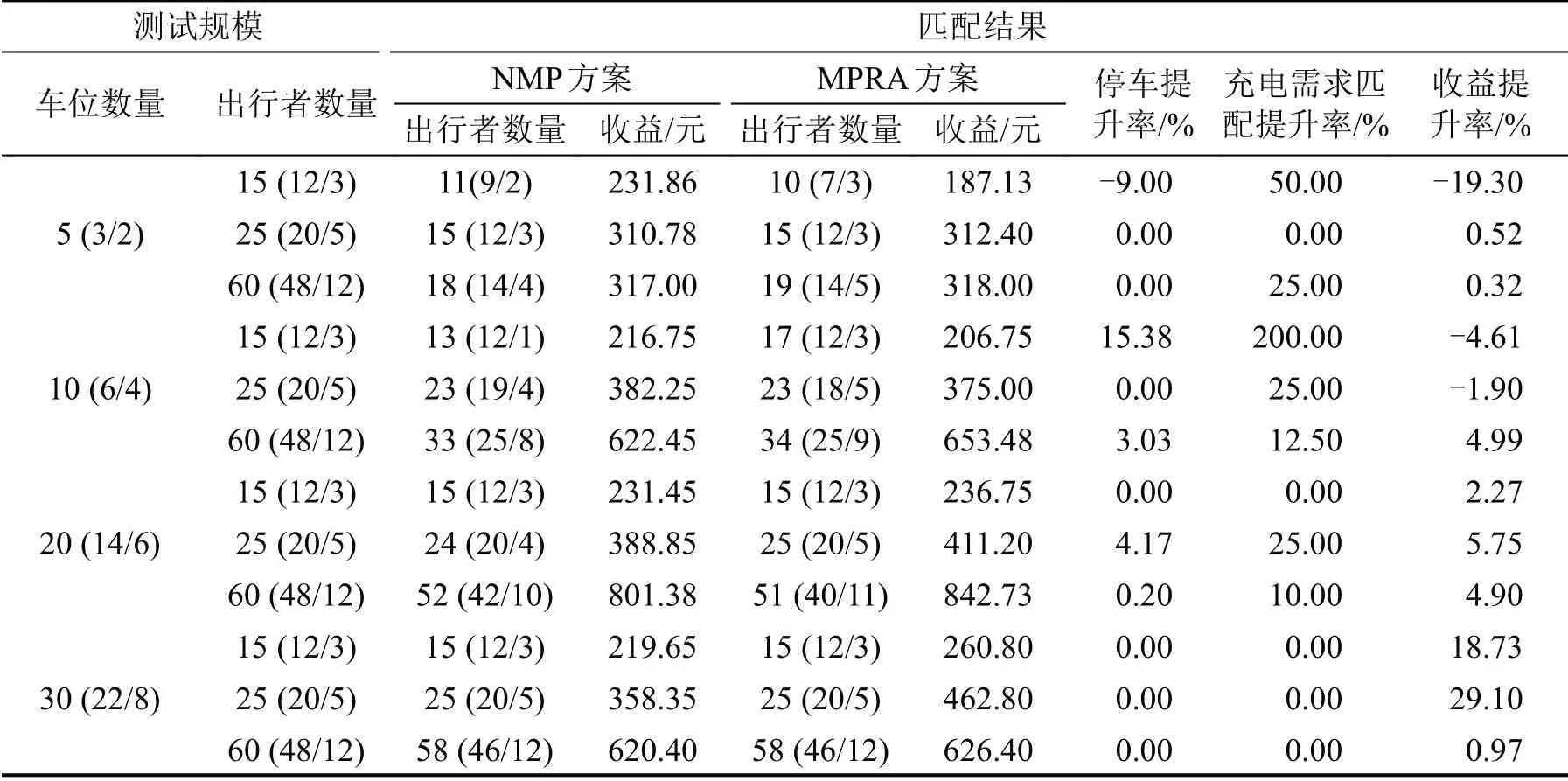
表4 MPRA方案与NMP方案在不同规模下的比较结果Table 4 Comparison results of MPRA and NMP at different scales

4 结论

本文创新性地提出考虑匹配优先级的混合车位租用和分配(MPRA)方案，构建整数规划模型实现平台运营商利润最大化。通过算例分析得知：

(1)出于平台运营商利润最大化考虑，NMP 方案会将停车时段较长的停车需求分配到充电车位，导致充电资源浪费。MPRA 方案是在匹配优先级满足的前提下综合考虑平台利润下确定最终分配方案，因此在充电资源利用率方面高于NMP方案，平均提升率为28.96%。

(2)MPRA方案将需求和供给进行分类匹配和处理，使充电需求可以优先满足。与仅按照停车需求到达的先后顺序依次进行车位分配的FCFS方案相比较，在停车率和充电需求的满足率方面均具有优势，平均提升率分别为17.87%和113.96%。

(3)停车位数量稳定情形下，针对停车需求持续增加，特别是供需差距悬殊的混合停车场，MPRA 方案在平台收益和充电需求满足率方面均高于FCFS方案和NMP方案。

(4)对于停车需求稳定情形下，随着平台可接受的停车位数量的增加，MPRA在停车率和充电需求匹配率方面的优势降低，但平台收益优势逐渐增加，平均提升1.34%。