基于动态时间调整的时空图卷积路网交通流量预测

刘宜成，李志鹏，吕淳朴，张涛，刘彦*

(1.四川大学，电气工程学院，成都 610065；2.清华大学，自动化系，北京 100084)

0 引言

随着社会的高速发展，智慧城市等新兴概念逐渐融入人们的生活。智能交通系统(Intelligent Transport System,ITS)是智慧城市的重要组成部分。其中，交通车流量预测是ITS的研究关键。精准的交通流预测对保证公众安全和解决交通拥堵等具有极其深远的意义。

早期的交通车流量预测是建立在传统统计学模型的时序序列预测。典型的如AHMED等[1]针对高速公路上的交通流进行预测，将流量预测问题转换成时间序列预测问题，提出差分自回归移动平均模型(Auto-Regressive Integrated Moving Average,ARIMA)的方法，ARIMA模型主要用于处理线性关系，然而，交通流数据通常是随机的和非线性的，导致该类模型对交通流数据关系建模不充分，预测精度不高。随着深度学习模型在很多领域取得了非常优秀的效果，越来越多的研究人员使用深度学习处理交通流量预测等问题。WANG 等[2]结合长短期记忆模型(Long-Short Term Memory,LSTM)和循环神经网络(Recurrent Neural Network,RNN)对短时交通流进行预测研究。LI等[3]针对高速公路交通流预测问题，集成卷积神经网络(Convolutional Neural Network,CNN)，LSTM，门控循环单元(Gate Recurrent Unit,GRU)等多种学习框架，提出一种多特征的高速公路交通流预测模型，有效提升了高速公路的交通流预测精度。为了保证构建更深的CNN 时避免梯度消失和梯度爆炸等问题，研究人员将残差网络(Residual Network,ResNet)与CNN相结合。ZHANG等[4]结合残差网络和CNN提出了基于深度学习的时空数据预测模型，预测城市人流量。然而，传统的CNN本质上只适用于欧氏空间，对于复杂拓扑结构的交通网络数据只能提取其中的局部特征。随着图卷积神经网络(Graph Convolution Network,GCN)的发展，能够有效提取网络数据复杂特征的GCN 成为了最佳的解决方案。ZHANG 等[5]结合LSTM 和图卷积捕捉城市交通流数据的时间规律性和时空关联性，有效修复了缺失的交通流数据信息。CHEN等[6]提出基于图卷积网络的大规模城市路网短时交通流预测模型，预测真实大规模城市路网浮动车数据，验证了图卷积网络优秀的预测性能。GUO 等[7]提出一种结合注意力机制和时空图卷积网络，解决交通流预测问题，通过时空注意力机制有效地捕获了交通流数据中的动态时空相关性，在美国加利福尼亚州高速公路公开数据集上进行实验，表明该预测算法优于之前的预测算法。

然而，现有算法对交通流时空关系的建模通常只考虑时间维度上的关联性或者空间维度上的关联性，未能够在时空关系建模中充分考虑时空相关性的问题，建模不够充分。本文对此提出了基于时空注意力机制和残差网络的时空图卷积网络的交通流量预测模型(TSARGCN)。模型的输入端将输入数据按照其时间维度特性分为邻近信息片段、相关信息片段和历史信息片段这3个分支模块，使用计算时序序列相关性最常用的DTW(Dynamic Time Warping)算法定义时间图的概念，结合交通路网空间结构的空间图定义时空关系图的概念。在分支模块中，考虑到梯度爆炸或者梯度消失等问题，引入残差网络层保证网络的收敛；为充分捕获交通流数据中的时空关联性特征，结合时空关系图和注意力机制，建立图卷积神经网络和时间维度卷积网络。在模型输出端对分支输出加权融合得到预测结果。在公开数据集上，对本文提出的模型进行实验验证，并与常见预测模型进行性能比较。实验表明，本文提出的模型有效提升了交通流量预测的精度，相较常见预测模型可以更精准地预测交通流量。

1 问题描述与建模

1.1 交通流量预测问题定义

本文研究基于道路结构及历史交通流相关信息预测未来某段时间内某路段的交通流量。用于采集交通流数据传感器的采集频率通常为1次·min-1，采集的交通流数据通常包括车流量和车速等。考虑按照原始数据量过大的问题，本文将数据集按照5 min时间步长进行数据整合处理。处理后数据集中第1个时间节点作为时间起始点，定义节点i的第t个时间步长的交通特征数据为Xi(t)∈R(F)，F表示节点用于采集的传感器采集总数量，即特征数量。定义节点i的历史T时间步长总的历史矩阵为Xi=[Xi(j)|j=1,2,…,T]，j表示时间序列标号；N个节点总的交通流历史数据表示为X=[Xn|n=1,2,…,N]，其中，n表示节点标号。本文研究内容为通过X预测各个节点在第T个时间步长后未来Tx时间步长的交通流量。

1.2 空间路网结构图

空间路网结构的无向图G(V,E)如图1所示。

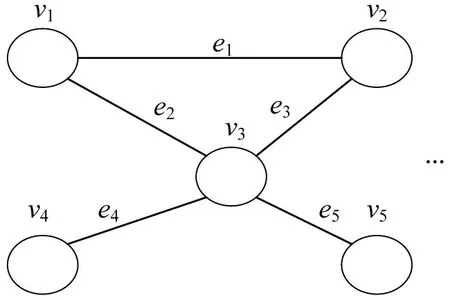
图1 空间路网结构Fig.1 Structure diagram of space road network

将使用的交通流量传感器所在的空间位置视作空间结构图中的节点，则V={v1,v2,…,vn}表示节点的集合；E={e1,e2,…,es}表示连接节点的边集合，s表示空间路网结构图中边的总个数；邻接矩阵A表示节点之间的相邻关系，A中仅包含0 和1 两种元素，其定义为

空间路网结构图中各个节点之间的邻近关系，将会在2.3 节中利用，进而实现交通车流量更精准的预测。

2 交通流量预测模型

本文提出的网络架构如图2所示。模型主要包括以下几个部分：时间序列分割模块，残差网络层，引入注意力机制的图卷积层，引入注意力机制的时间卷积网络层，加权融合输出端。图2 中，Input Flow为交通数据集；Xc,Xp和Xd为输入数据集经过时间序列分割模块分割的临近信息片段、近期信息片段和历史信息片段；GT为输入数据集通过DTW算法建立的时间图和根据节点之间邻近关系建立的空间图融合而成的时空关系图；RESNET为残差网络层；GCN 为图卷积层；Conv 为时间卷积层；Fusion为加权融合输出端；ΓS、ΓT分别为3个模块分别求取的空间注意力权值矩阵、时间注意力权值矩阵；Yc,Yp和Yd分别为3 个模块的交通车流量预测；Y为最终的交通车流量输出。

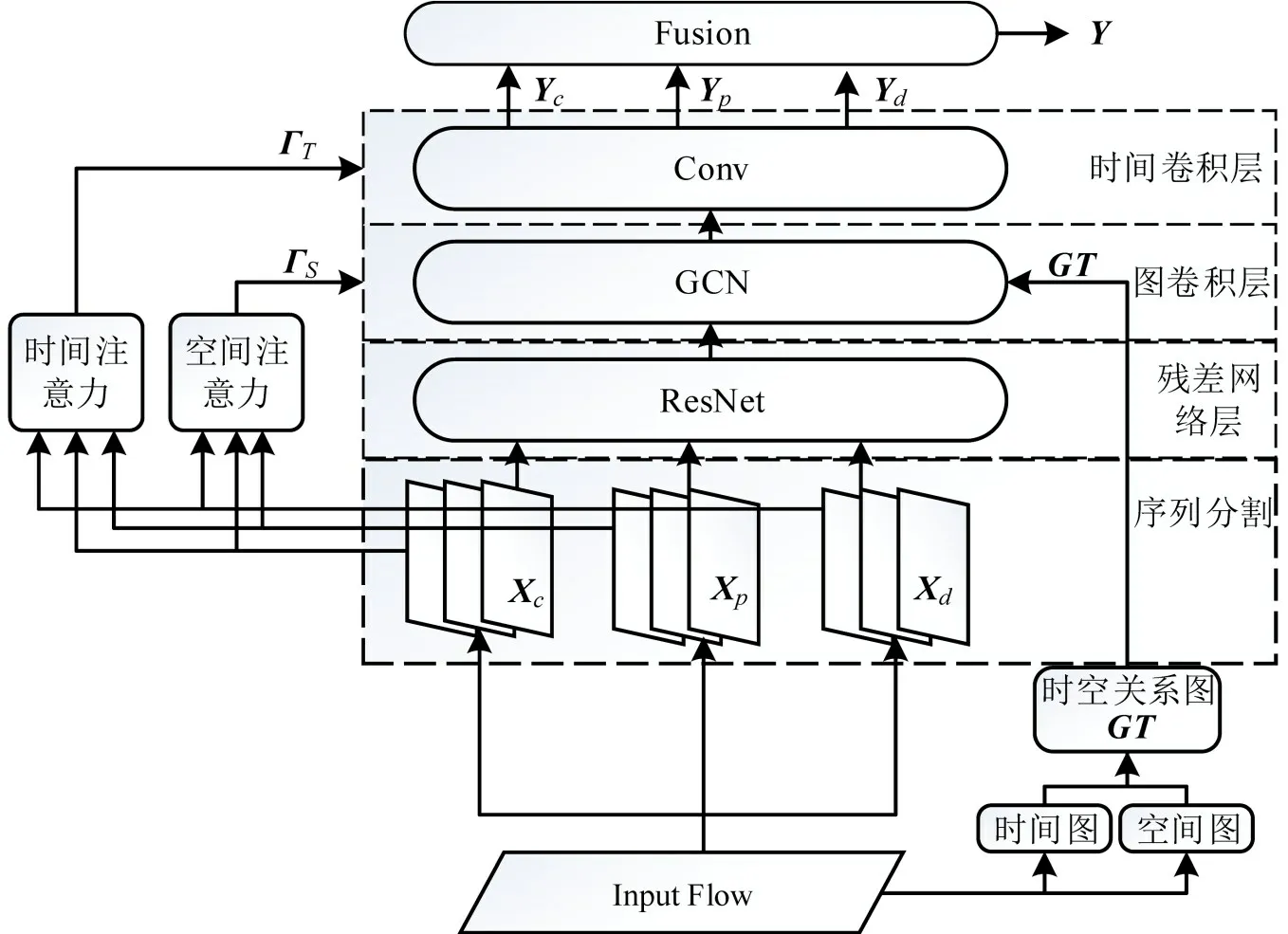
图2 TSARGCN网络整体结构Fig.2 Overall structure of TSARGCN network

2.1 输入序列切分

考虑到交通数据在时间维度上的数据周期性、邻近性等特征，将输入部分划分为邻近信息片段，近期信息片段和历史信息片段3 个部分以提取特征。如图3所示，以预测X(T)之后Tx时间步长内的交通流量为例，则输入序列进行如下分割。

图3 输入序列切分片段示意图Fig.3 Schematic diagram of input sequence segmentation

邻近信息片段选择为

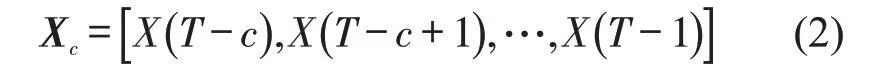
近期信息片段选择为

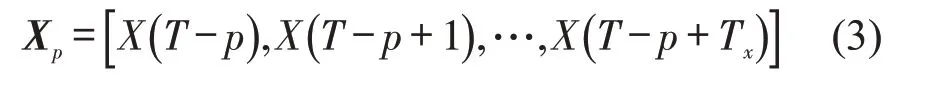
历史信息片段选择为

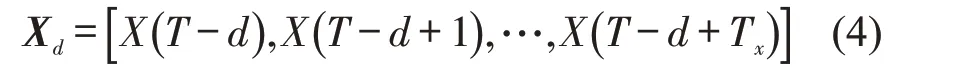
参数取值如下：待预测序列长度为Tx=12，即预测未来1 h 的交通流量数据；邻近信息片段序列长度选择为c=36，即选择待预测片段前3 h 的交通流数据；近期信息片段选择p为1 d的时间步长，即待预测片段前一天的该时刻的交通流数据；历史信息片段选择d为1周的时间步长，即选择前一周的该时刻的交通流数据。

2.2 残差网络层

为实现对交通流数据时间特征以及空间特征的有效提取，在模型中常常需要堆叠多个卷积层进行时空特征的挖掘。然而随着卷积层的堆叠，整个网络模型会出现梯度弥散等问题，即在损失函数减小到一定数值后，随着训练的增加会导致损失函数不再变小甚至增加，因此导致训练的整体精度下降。针对上述问题，本文引入残差单元结构用以提高整个模型的训练精度。残差单元结构组成的网络因为其训练学习过程中恒等函数的易得性有效解决了梯度弥散等问题。如图2所示，对经过2.1节切片后输入的3 个分支均加入一个残差网络进行训练。每一个残差网络由多个残差单元组成，每一个残差单元则由2 个卷积层(Conv)，2 个批量归一化(Batch Normalization,BN)处理层和1 个Relu组成。

卷积层使用3×3的卷积核提取输入的特征，其操作如图4所示。图中，X为输入，⊙p为分块哈达玛积，Xo为卷积后的结果，即经过卷积层输出的特征。

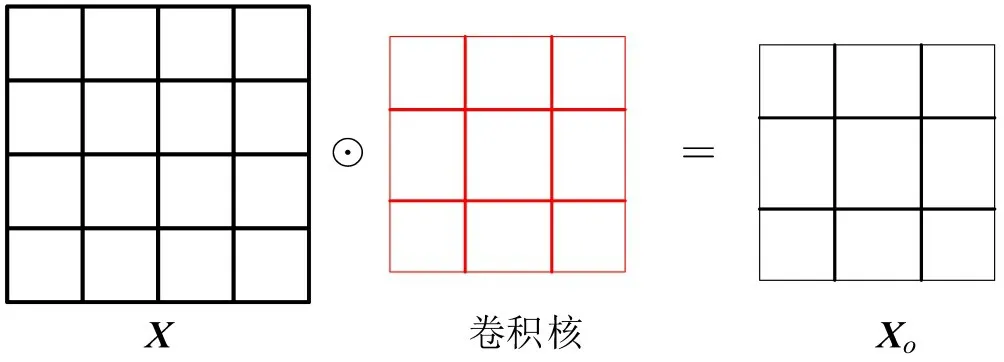
图4 卷积层操作Fig.4 Convolution layer operation

BN 层即批量归一化处理，常用于减少内部变量偏移进而加速神经网络的训练，计算过程如图5所示。图中，X为输入，u为均值，σ2为方差，为标准化处理后的元素，为线性变换后的元素，Y为BN层的输出，γ,β为可训练的参数。

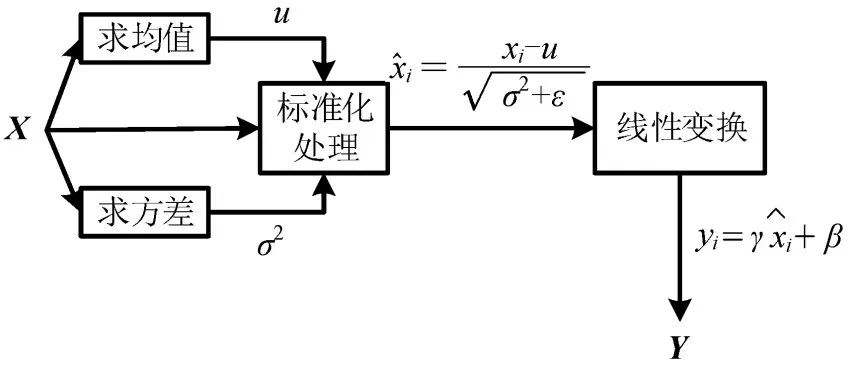
图5 BN层操作Fig.5 BN layer operation

Relu为一种激活函数，计算公式为

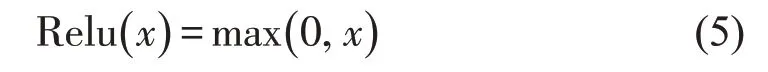
其计算简易性使网络的收敛速度很快，其输出的稀疏性可防止出现过拟合现象。

以Xc输入为例，通过上述网络结构组成残差网络结构图如图6所示。

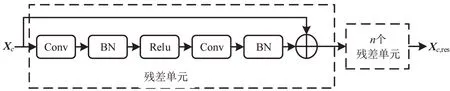
图6 残差网络结构图Fig.6 Structure of residual network

2.3 基于DTW算法建立时空关系图

DTW[8]是一种典型的计算两个时间序列相似程度的算法，且为一种优化调整算法，即通过一对多以及多对一匹配的方式使得两个时间序列之间总距离最小化的最优匹配方法。本文利用DTW思想构造不同节点之间车流量数据的时间关联矩阵。对于任意两个节点i和节点j的车流量序列分别为

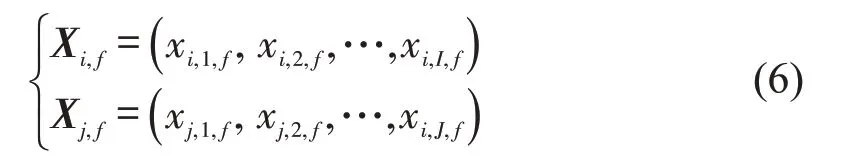
式中：Xi,f、Xj,f分别为节点i、节点j的交通流量数据集合；I、J分别为两个序列的总长度。

在相似程度的比较时，通常采用的量化指标为两个序列中各点之间的欧氏距离，用欧式距离函数d(m,l)表示，即

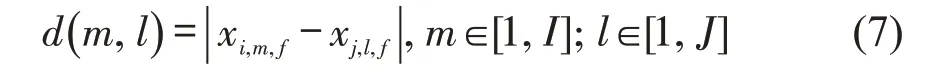
式中：m为节点i的车流量序列中第m时间点；l为节点j的车流量序列中第l时间点。计算两个序列之间各点欧氏距离，用表示两个序列总的相似程度大小。则其计算的具体方法如下。

定义规整路径L=(l1,l2,…,lE)作为衡量两个序列之间匹配代价大小的计算，如图7所示。

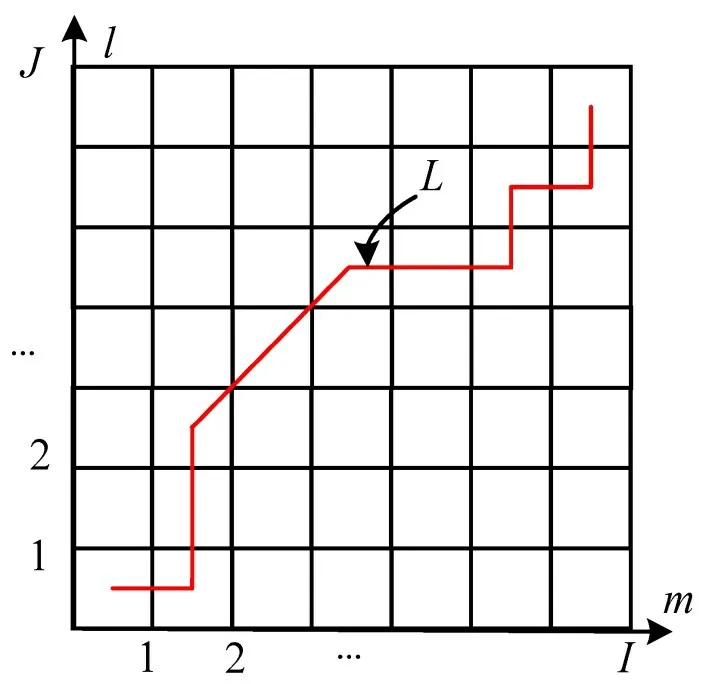
图7 规整路径示意图Fig.7 Outline path diagram

整个路径满足约束为

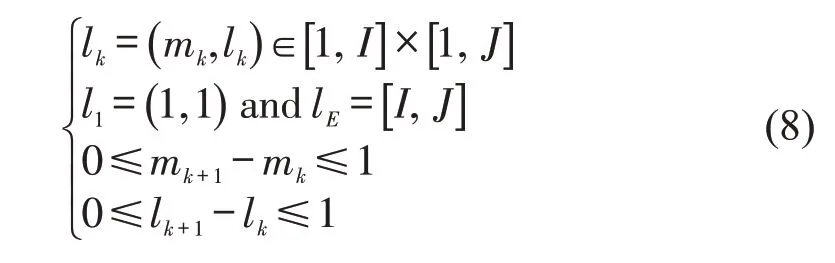
式中：lk为路径中经过的点在图7 中的坐标，。

定义两个序列之间的总匹配代价为

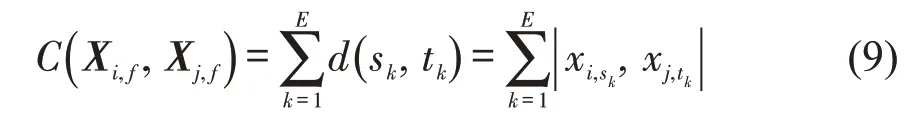
本文采用动态规划的思想递归求出最小总匹配代价，递归公式为

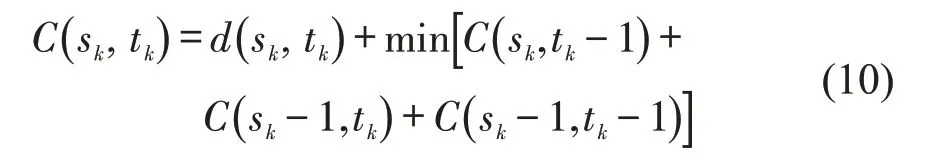
求取最终的最小匹配代价C(I,J)，即为两个序列之间的相似程度大小。

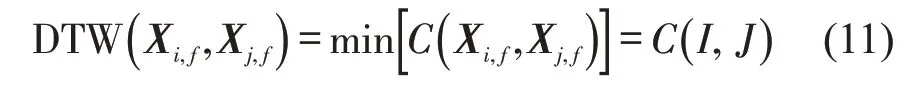
利用上述方法，分别计算每一个节点和其他节点整个时间序列的相似程度，定义n×n维的时间关联矩阵为

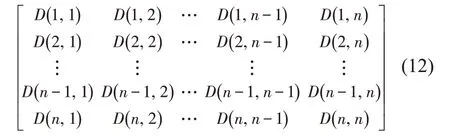
式中：D(i,j)为DTW。经过实验，在本数据集中时间序列相似度的取值范围为3100～4200，该相似度数值越小表示两个节点之间的交通车流量的变化模式越相近。

利用节点之间交通流量数据的时间序列相关性，建立路网结构中在空间路网结构中无法反映的流量影响关系，例如学校、医院等导致的流量变化。在空间节点之间可能不存在连接关系，但是因为社会作用相互影响的流量影响关系，将这种关系视作时间路网结构图中存在的连接关系。利用式(12)时间关联矩阵，结合1.1节中的空间路网结构图建立时间图。时间图定义为Tg=(V,D)，如图8所示。V为空间路网结构图中的节点集合，D为各个节点之间时间序列相似程度大小集合，D={D12,D13,…,Dn(n-1)}，其中的每个元素定义为Di,j=(i,j)。

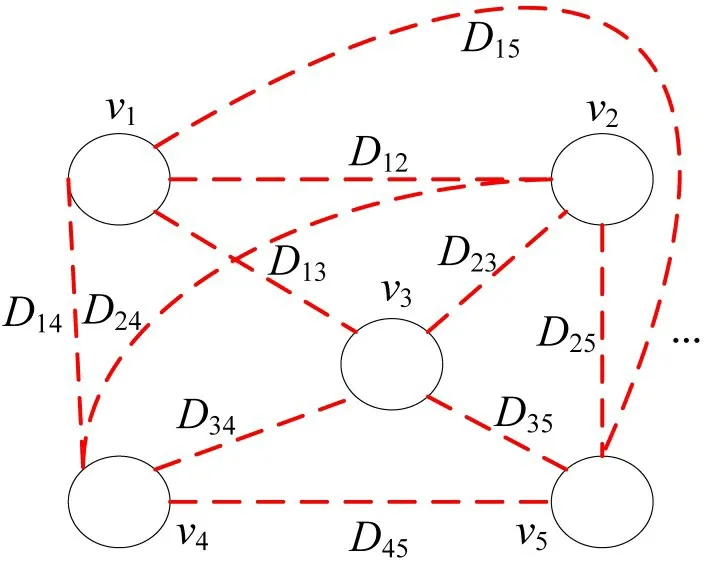
图8 时间图示意图Fig.8 Time graph diagram

给定时序序列相似度阈值，建立节点之间时间维度的时序关联矩阵A0。阈值作为区分两个节点之间时间序列是否相似，阈值以内的认为两个序列相似，即两个节点的流量之间存在一定的相关性。则时序关联矩阵A0为

式中：TThreshold为设置时间序列相似度阈值，在该阈值以内认为节点之间相互影响，即时间图中相邻。

结合时间图和空间图定义时空关系图如下：时空关系图结构中包括节点及邻近关系两个要素。在时空关系图GT(V,As)的构造中，节点集仍然为V；在考虑节点邻近关系时，为了更清晰地直观表示，融合邻接矩阵和时序关联矩阵得到GT图中的邻居矩阵As。通过邻居矩阵表征邻近关系，建立时空关系图如图9所示。

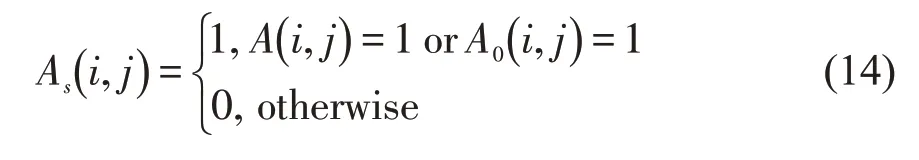
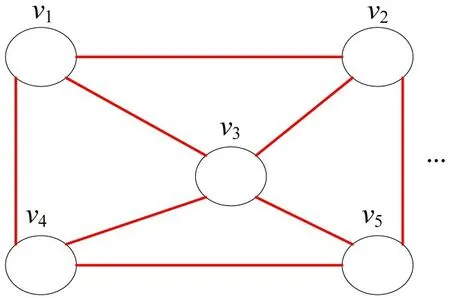
图9 时空关系图示意Fig.9 Diagram of GT

2.4 时空注意力权值

注意力机制是模拟人脑注意力，用于调整权重大小使模型对重要的信息给与更多的关注。考虑到交通流量中不同节点对各个节点的影响不同以及不同时刻点之间的互相影响不同，在图卷积和时间维度卷积之前分别加入一个注意力机制，该机制用于衡量不同节点输入特征以及不同时刻输入特征的重要性程度值。

以预测1.1 节中X0为例，输入历史数据为X={Xn|n=1,2,…,N}，空间注意力权值计算过程如下。

经过2.1 节处理后的邻近信息、近期信息和历史信息这3个分支的数据流分别为Xc,Xp和Xd，以Xc为例，多模式注意力网络在注意力机制中表现极佳，考虑多模式输入通道注意力分布计算成本过高的问题，采用双线性注意力的方式设计评价函数，构造出空间关联性矩阵IV,C为

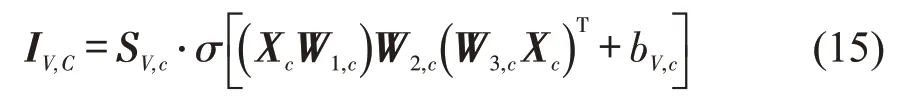
式中：SV,c∈RN×N,bV,c∈RN×N,W1,c∈RH,W2,c∈RF×H,W3,c∈RF均为待学习参数；W1,c为表征其H维度的权重；W3,c为表征其不同数据种类的权重，如车速在流量预测中的权重等；W2,c为表征H维度和不同数据种类维度权重之间的交互；Xc∈RN×F×H为所有节点全部数据；σ为激活函数；N为节点数目；F为数据种类数目；H为时间长度，邻近信息，近期信息和历史信息这3个分支的H选择上，考虑对当前交通车流量的历史影响最明显的为前3 个时间点，前一天的同一时间点和前一周的同一时间点，因此取值为36，12，12。根据空间关联性矩阵，接下来以邻近信息分支空间注意力权值矩阵为例，求取节点i与节点j之间空间注意力权值的表达式为

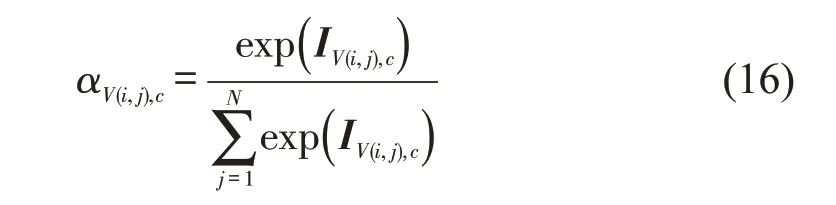
式中：IV(i,j),c为空间关联性矩阵中第i行，第j列的元素，表征的是节点i与节点j之间的空间维度关联程度；αV(i,j),c为节点i与节点j之间的空间注意力权值。对全部节点分别求取空间注意力权值可以获得空间注意力权值矩阵为

通过以上求解可以分别求出3 个分支的空间注意力权值矩阵ΓS,c,ΓS,p和ΓS,d。

类似空间注意力权值求取方法，类似空间注意力权值矩阵的方法求取输入的时间关联性矩阵，仍然以Xc为例求解。

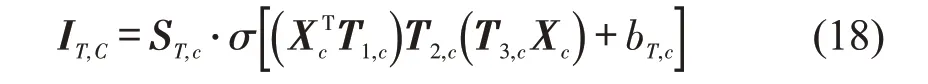
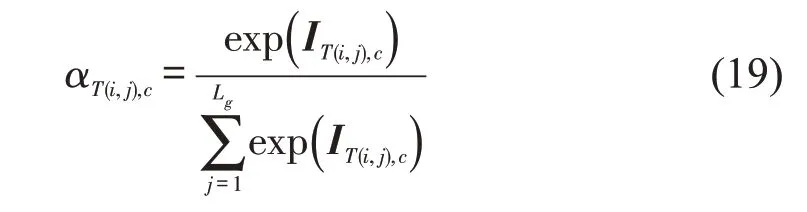
式中：IT(i,j),c为时间关联性矩阵中第i行，第j列的元素；αT(i,j),c为时间点i与节点j之间的时间维度关联程度。依次对每个时间节点分别求取时间注意力权值可以获得时间注意力权值矩阵为

通过以上求解可以分别求出3 个分支的时间注意力权值矩阵ΓT,c,ΓT,p和ΓT,d。

2.5 时空关系图卷积

通过2.3 节建立的时空关系图，使用图卷积的方式提取节点在时空关系图中的空间维度特征，这一特征不仅结合了路网结构中的空间关系，同时结合了节点之间时序序列相似性的时间维度关系，即时空相关性特征。具体做法如下。

整个图用其对应的拉普拉斯矩阵来表示，时空关系图的拉普拉斯矩阵L为

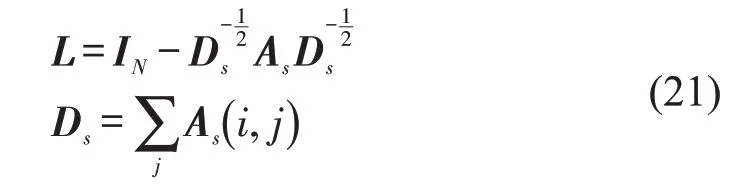
式中：As为2.3节求出的邻居矩阵；IN为单位矩阵。

对L进行特征值分解，即L=βΔβT，其中，Δ为L的特征值组成的对角矩阵，β为分解基。利用上述参数得到对输入历史数据进行图卷积计算的公式为

式中：Θg为图卷积核参数；Xg为经过图卷积之后的结果。

因式(19)计算相当复杂，故采用一阶切比雪夫多项式[21]对式(19)进行近似简化得到

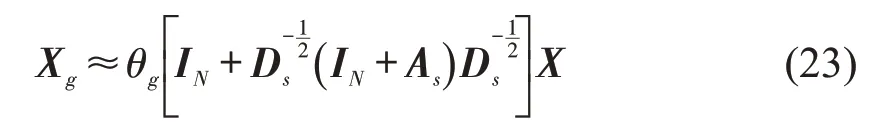
式中：θg∈R 为可训练的参数。

利用上述图卷积计算方式，结合2.4 节空间注意力权值矩阵，以经过2.2 节残差网络后的Xc,res为例，可以得到结合注意力机制的时空关系图卷积之后的结果为

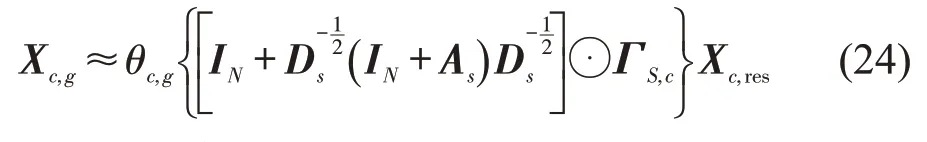
式中：⊙为哈达玛积。

按照上述方法可以依次计算出3 个分支经过时空关系图卷积之后的输出Xc,g,Xp,g和Xd,g。

2.6 时间维度卷积

经过2.5 节时空关系图卷积之后，为挖掘同一节点不同时刻交通流信息的相互作用关系，即时间维度特征，利用图10所示的时间维度卷积进行操作。

图10 时间维度卷积示意图Fig.10 Schematic diagram of convolution of time dimension

在每个分支分别引入时间注意力权值矩阵，结合二维卷积实现时间维度的特征提取，图11 展示了Xc,g通过该层处理操作。

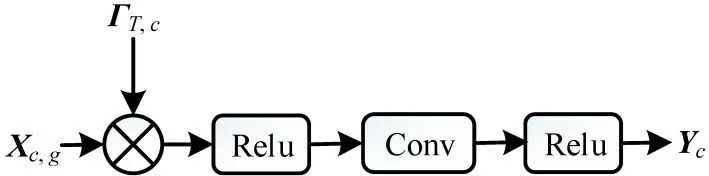
图11 时间维度卷积网络结构图Fig.11 Time-dimension convolutional network structure diagram

通过时间维度卷积，可以得到3个分支的输出分别为Yc,Yp和Yd。

2.7 特征融合

将2.6 节输出结果进行线性加权融合，得到流量预测结果为

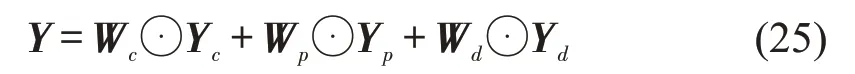
式中：Wc,Wp和Wd为3 个可学习的参数；Y为最终流量预测值。

3 实验与结果分析

3.1 数据集

为了评估模型，本文在PEMSD4数据集中进行了大量的对比实验进行验证。

PEMSD4 是2018年1～2月美国旧金山湾区307 个监测点收集到的数据，这些数据被整理成每5 min 一条记录，包括流量，车速和车道占有率这3个维度的数据。

实验数据集按照6∶2∶2的比例划分为训练集、验证集和测试集。本文在图卷积和时间卷积中使用32 个1×3 的卷积核，预测时间步长c为12，，学习率设为0.001，批次大小为64，使用均方误差为损失函数，利用Adam 作为优化器进行优化，模型的迭代次数设置为100。

3.2 模型评价指标

本文选择模型的评估函数为平均绝对误差(Mean Absolute Error,MAE)函数和均方根误差(Root Mean Square Error,RMSE)函数。MAE 用于反映预测值误差的实际情况，RMSE则用于反映均方误差的算术平方根。具体计算公式为

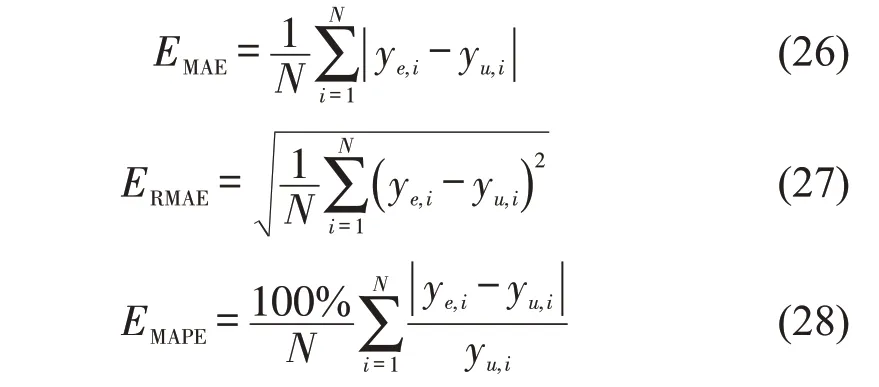
式中：ye,i为交通流量预测值；yu,i为交通流量真实值。

3.3 数据预处理

为了消除交通数据中交通流量过大或者过小对整体预测带来的不利影响，本文采用Z-score 方法进行数据标准化，计算公式为

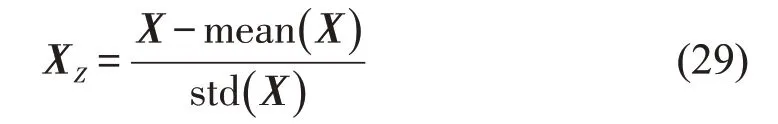
式中：mean(X)为序列的均值；std(X)为序列的标准差。

3.4 残差网络实验

为了测试不同残差网络深度对整个模型预测性能的影响，研究不同深度MAE值的不同表现，结果如图12所示。从图中可以看出：一开始随着残差网络单元个数的增多，整个网络的预测性能得到明显提高；当残差网络单元超过16个的时候，整个网络的预测性能开始变差，分析其原因可能是由于网络过深导致训练难度加大进而降低了整个网络的预测性能。因此，实验中设置残差网络单元个数为16，实现最佳预测效果。

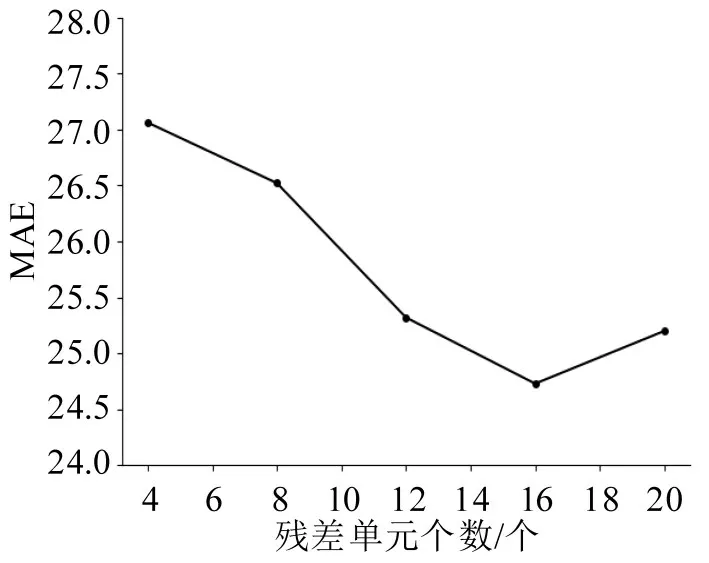
图12 残差网络单元个数对MAE的影响Fig.12 Influence of number of residual network units on MAE

3.5 时间图阈值实验

构造时间图时，定义了一个阈值(Threshold)来建立节点之间时间相关性，不同的阈值对于整个网络的预测性能存在一定影响。因此，通过改变不同阈值建立不同的时间图进行多次训练，验证整个网络预测性能最佳的效果，结果如图13所示。在保证整个网络其他结构不变的情况下，阈值设定为3300 时，取得最佳预测效果。在设定阈值为3300的时候，时间图中各个节点的相邻节点个数保证在5个左右。阈值设定为更小时，相邻节点数量较少，不能够有效提取时间维度的关联关系；设定更大时，相邻节点数量过多导致整体预测效果变差。

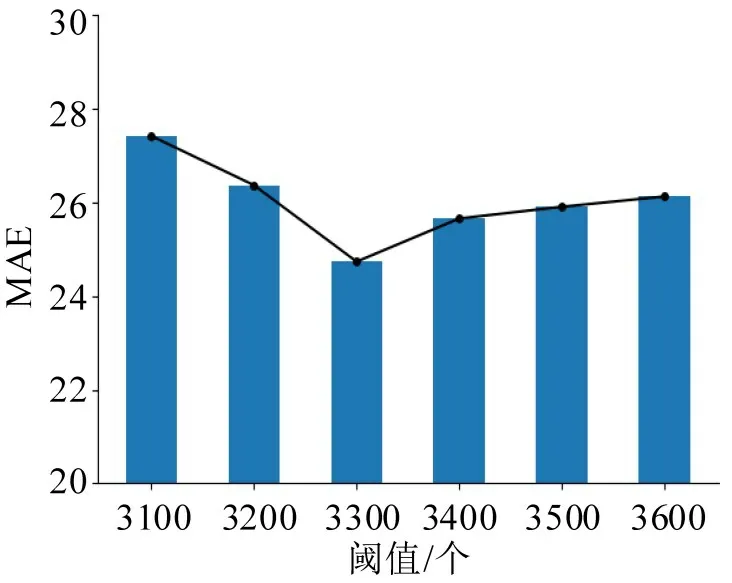
图13 时间图阈值对MAE的影响Fig.13 Effect of time graph threshold on MAE

3.6 实验结果分析

为评估本文模型的预测性能，选用如下模型进行对比分析。

(1)HA(历史均值法)。本文实验设置上利用过去1 h 的流量均值预测下一个时间片的交通流量值。

(2)SVR(支持向量回归法)。本文选取的核函数为径向基函数，其中核系数设置为0.1。

(3)ARIMA(自回归积分滑动平均法)。一种时间序列预测分析的经典模型，模型简单且不需要借助其他变量。

(4)Conv-LSTM(卷积长短时记忆网络)。在LSTM 的基础上添加了卷积神经网络，实现比LSTM更强的特征捕捉能力，进一步提高了时间序列的预测效果。

(5)ASTGCN(结合注意力机制和时空图卷积网络)。该模型不仅考虑了时间周期性特征，同时结合了图卷积操作提取融合了空间特征的时空网络。

实验采用tensorflow 和mxnet 等框架实现上述模型的架构和实验仿真，对PEMSD4 数据集中的307 个节点的交通车流量进行预测，结果对比表如表1所示。

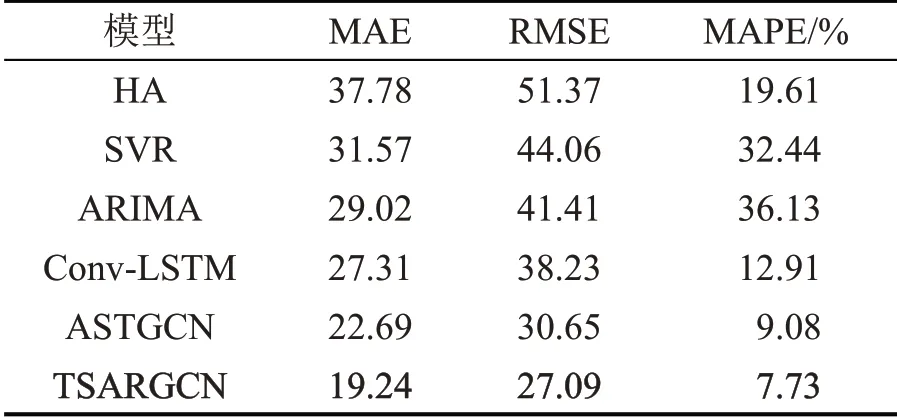
表1 TSARGCN与其他模型实验结果对比Table 1 Comparison of TSARGCN and other models

从表1 中可以看出，对未来1 h 的流量预测实验中，本文提出的TSARGCN 模型在MAE，RMSE及MAPE 等指标中均获得了更好的效果。SVR 相对于HA 而言提高了对交通流信息非线性特征的提取，而ARIMA则是通过将自回归、移动平均和差分等传统统计学方法相结合实现了对交通流时序依赖关系的建模，但其只能捕获线性关系，在复杂交通网络结构中的流量预测具有较大的局限性。Conv-LSTM 是在LSTM 添加了卷积操作，不仅获取了时间信息流同时提高了对空间信息流的处理。ASTGCN则是引入图卷积和注意力机制，明显比普通卷积操作更符合流量预测的需求。这是因为在复杂交通网络结构中，图卷积相对于普通卷积而言，能够更好捕捉交通流量数据的空间特征，注意力机制可以更好地动态调整网络模型参数，进而实现了预测精度的有效提高。对比ASTGCN 和本文提出的TSARGCN 的指标参数可以看出，TSARGCN 的效果明显更好，究其原因在于ASTGCN 进行的图卷积操作中考虑的节点邻近关系仅仅为空间图中的邻近关系，而TSARGCN 则是通过DTW算法构建节点之间交通车流量模式相似关系，建立了时间图表征节点之间潜在的交通车流量影响关系，再在此基础上进行图卷积对整个路网的结构解析更深，对于时空特征的相关性特征有更好的捕捉效果，对于时空特征的融合效果更佳，进而提高了模型的预测性能。

TSARGCN 对于不同节点的交通车流量预测结果存在一定的差异，表2 为TSARGCN 在几个节点的预测能力，53号节点是整个预测中误差最大的节点，204 号节点是误差最小的节点。图14 为TSARGCN 在0 号、1 号及2 号节点共3 个不同节点的两种交通流量模式的预测能力。在交通流量变化趋势中，由于节假日等因素导致人们作息不同，因此存在“单峰”“双峰”两种交通流量模式。图14(a)、(b)分别展示了0号节点“单峰”“双峰”的真实数据趋势和TSARGCN 模型预测流量数据趋势。“单峰”模式下，人们活动时间集中在12:00-18:00，这种模式通常出现在节假日期间(人们通常在下午进行外出活动)。TSARGCN 在这种模式下能够较好地预测实际交通流量的变化趋势。“双峰”模式下，通常会在9:00 左右和18:00 点左右出现两个高峰，这符合工作日因为上下班出行导致的早高峰和晚高峰。TSARGCN 在这种模式下能够明显捕捉早高峰和晚高峰的峰值时间点，同时能够比较精确地跟踪交通流量变化。为了评测不同节点该模型的交通流量预测能力，还给出1 号和2 号传感器节点在两种模式下的实际流量曲线和预测流量曲线，如图14(c)～图14(f)所示，从中可以看出，该模型能够较好地预测出不同节点交通流量的趋势。

表2 TSARGCN在不同节点的预测指标Table 2 Comparison of TSARGCN and other models

结合表2 和图14，0 号节点的预测效果是3 个节点中最好的。从0号，1号和2号这3个节点预测中可以看出，流量数据的变化越标准，预测值与真实值越接近。通过研究发现，误差的主要来源在于“双峰”模式下的双峰标准程度。“单峰”模式下的流量预测都相对精准，而“双峰”模式中波峰高度之间的差异，波峰与波谷之间的差异成为影响标准程度的关键。

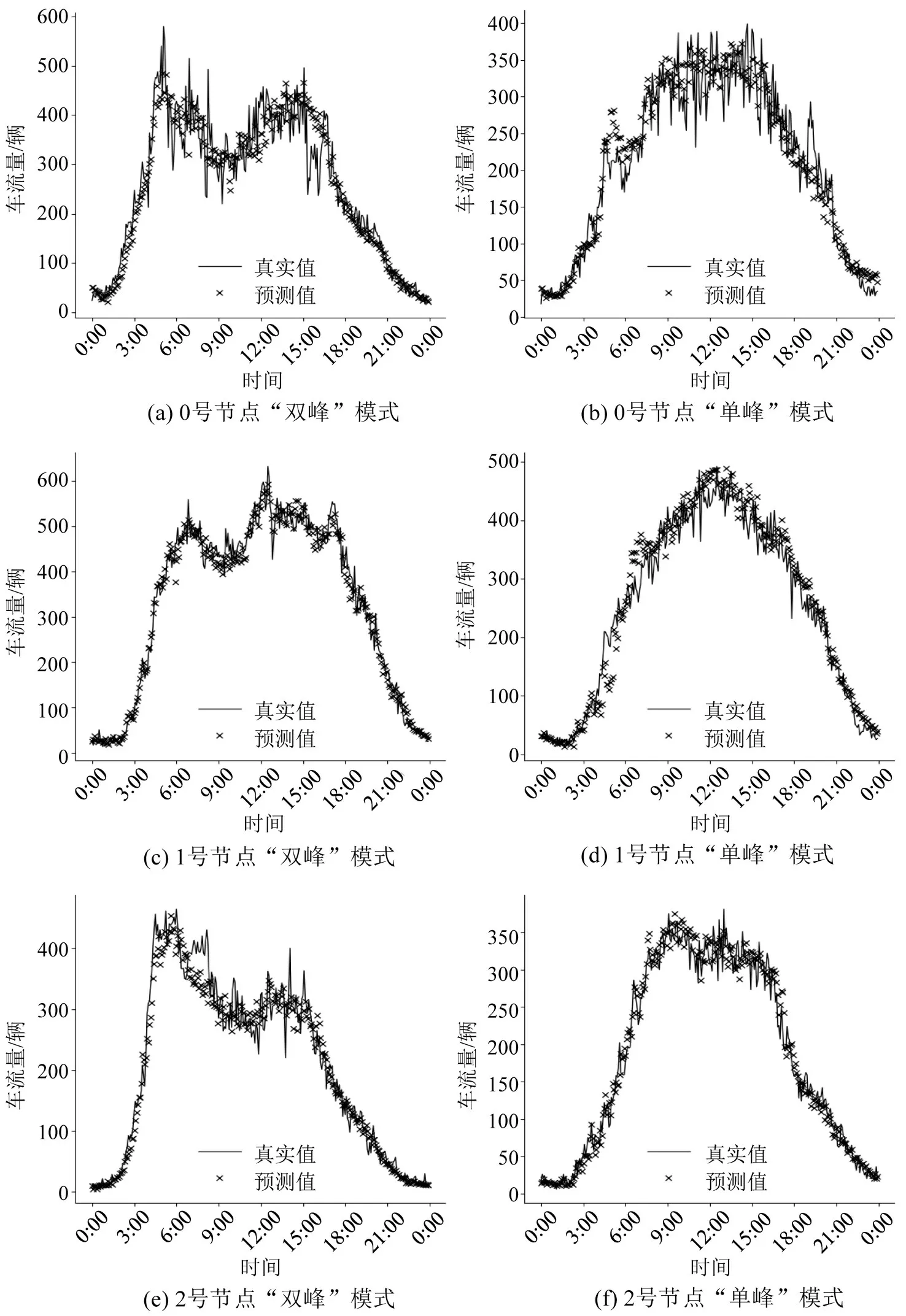
图14 TSARGCN在不同节点的交通流量预测图Fig.14 TSARGCN traffic flow prediction graph at different nodes

在表2 的基础上，进一步研究了不同节点在“双峰”模式下的双峰标准程度对流量预测的影响。首先针对原始数据进行简单的平滑处理，考虑本文实际数据起始点和真实数据时间点并没有完全对应，观察0 号，1 号，2 号节点数据特征之后，本文将6:00 左右的流量值作为左峰值点，14:00 左右的流量值作为右波峰点，10:00 左右的流量值作为波谷点，统计波峰波谷点的数据，如表3所示。通过表3 的各个数据可以看出，当两个波峰值越接近，波谷值与波峰值差距越明显，则双峰模式标准程度越高，流量预测精度也就越高，预测值和真实值越接近。

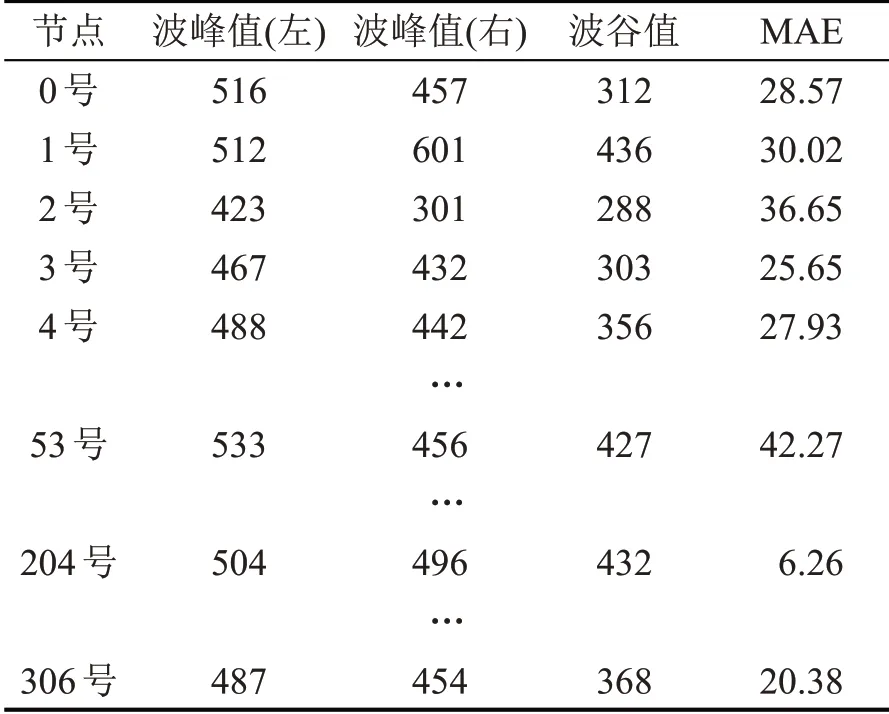
表3 不同节点的波峰波谷值对流量预测的影响Table 3 Influence of peak and trough values of different nodes on flow prediction

图15 为TSARGCN 在0 号节点2018年1月1～7日共1 周的交通流量预测结果图，从图中可以看出，模型能够很好地跟踪每天的流量变化趋势。该模型对整个流量变化的时间周期性以及不同节点之间相互影响导致的时空相关性实现了较好的捕捉。

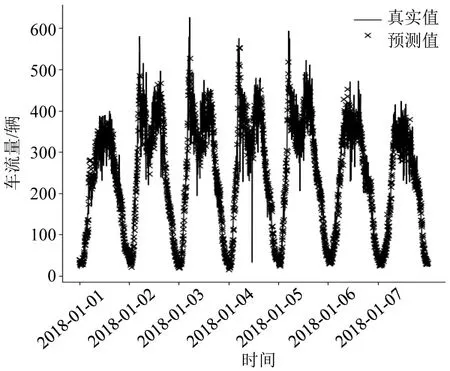
图15 TSARGCN在0号传感器1周的交通流量预测图Fig.15 TSARGCN weekly traffic flow forecast at sensor 0

4 结论

本文得到主要结论如下：

(1)提出的TSARGCN 交通流量预测模型与HA，SVR，ARIMA，Conv-LSTM 以及ASTGCN 等交通流量预测模型相比，因TSARGCN充分考虑了交通流中时空特征及其相关关系，交通流量预测精度明显高于其他模型。

(2)通过对0 号、1 号和2 号这3 个节点不同交通流量模式的预测结果分析可知，在不同节点，TSARGCN 都能较好地预测各种交通流量变化趋势。

(3)通过对0 号节点2018年1月1～7日共1 周的交通流量预测结果分析，TSARGCN对整个交通流量在1周内的变化都能够较好地预测。