过饱和地铁线路的列车容量分配策略及优化模型

石俊刚，秦昙，李响，杨立兴，杨晓光,3

(1.华东交通大学，交通运输工程学院，南昌 330013；2.北京交通大学，轨道交通控制与安全国家重点实验室，北京 100044；3.同济大学，交通运输工程学院，上海 201804)

0 引言

地铁系统因其容量大、方便、快捷等特点，逐渐在各个城市得到广泛应用。随着地铁网络的不断发展，越来越多的乘客选择地铁出行，客流的不断增长使地铁运营承受着巨大压力。虽然受疫情影响，2020年以来地铁客流量有所下降，但北京、上海、广州的日均客流量仍超过800 万人次，且逐步得到恢复。面对规模庞大的客流，部分地铁线路时常出现过饱和情况，造成部分车站客流严重拥堵，为运营安全带来较大风险。

为缓解线路拥堵，列车时刻表优化和调整是目前常用的手段。其主要是根据客流需求，对列车运行计划进行优化调整，以减少乘客的等待时间，缓解车站客流拥堵。旅客列车时刻表优化通常以运营成本、列车运行安全、客运服务水平等为优化目标。Yang 等[1]建立关于列车能源消耗和乘客总旅行时间最小化的双目标函数模型。Niu等[2]以等待乘客数量和站台剩余乘客数量最小化为目标。通过对现有研究进行归纳，可以发现，目前主要从调整列车运行交路、优化车站停留时间及发车时刻等角度入手，为线路上的瓶颈区段提供更充足的运能，其中包括采用大小交路、向拥堵车站加开备车等方式。其中，冉昕晨等[3]构建了关于大小交路和列车放空运行的运行图优化模型，以此达到列车节能和乘客节时的目的。然而上述研究仅对时刻表这一因素进行优化，学者们从全局的角度出发，考虑时刻表与列车停站方案或客流控制的协同优化。孟凡婷等[4]基于跳停策略对列车运行图和车站限流进行协同优化。卢亚菡等[5]考虑换入客流，对时刻表和车站客流控制进行协同优化，有效提高列车服务水平。对于工作日及节假日高峰时段，许多学者关注面向时变客流的列车时刻表优化问题，根据乘客的时变需求对列车时刻表进行优化，从而实现服务客运服务质量的提升。祁奇等[6]运用时空网络的方法将时刻表优化问题转化为路径选择，并分别考虑均衡客流和非均衡客流情况下时刻表优化模型，有效降低乘客的等待时间。许得杰等[7]考虑乘客时变需求，从多交路角度对列车时刻表问题进行优化。对列车时刻表进行优化能够有效地提高线路运输能力，缓解地铁线路的拥挤情况。但在客流量极度饱和的地铁线路，特别是一些市郊通勤线路，即使最大化列车的发车频率仍然无法缓解部分车站的客流超拥堵现象，如北京大兴线、昌平线等。

为缓解过饱和线路局部车站的极端拥堵情况，本文从线路层面出发，提出一种简单新颖的车厢容量分配方法，以均衡各车站客流聚集，确保拥堵车站乘客得到公平服务，进而提高整个线路运营安全性。具体的，通过控制每列服务列车在各车站投入运营的车厢数来动态分配各列车在各车站的可用列车容量，综合协调各车站内得到服务的乘客数(即登车人数)，实现各车站客流的均衡聚集，从线路层面提高总体运营安全性，并尽可能保证服务水平。

1 问题描述

地铁通勤客流具有较强的潮汐现象，如早高峰大部分乘客均从郊区方向前往市区通勤。此时，在上游车站由于列车容量较为充足，绝大部分乘客均能登上列车，不会造成客流拥堵。当列车驶向下游车站时，由于剩余容量逐渐减小，导致下游车站乘客难以上车，极易引发严重的客流拥堵。为缓解下游车站的极端拥堵情况，本文通过合理分配车厢容量来均衡线路上各车站客流聚集，以到达“削峰填谷”效果，提高线路的整体运营安全性。以图1 为例，图中矩形方块代表车站，采用集合S表示，列车从车站1驶向终到站 |S|。列车内矩形方块代表列车车厢，带有交叉符号的矩形方块代表为下游车站预留的车厢。以图1 中2 列列车为例，列车1 从车站1出发并预留3节车厢，当其到达车站m时释放2节车厢并于车站|S|-1 释放1节车厢。同样地，列车2在起点站预留2节车厢，当其到达车站|S|-1时释放所有预留车厢。

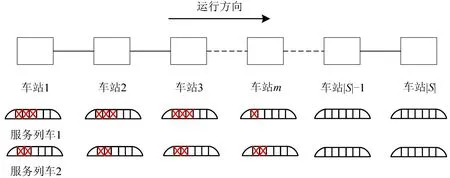
图1 列车容量分配说明图Fig.1 Illustration of train capacity allocation

为方便实际运营，每列车仅在始发站预留车厢，在运行的后续车站，只需要根据需求进行车厢释放。因此，车厢的预留数会随着列车的运行逐渐减少。本文通过构建数学模型，求解合理的车厢预留与释放方案，以均衡线路的客流聚集，提高线路的整体运营安全性。

2 模型的构建

2.1 模型假设

为方便问题模型构建，设置如下假设条件：

假设1 对于任意列车，在某个车站登上该列车的人数中前往不同目的地的客流比例固定。当线路处于过饱和状态，存在大量二次等待情况，考虑乘客出行起讫点来推算列车载客量会导致问题存在非线性特性，难以求解。此假设能够大大简化列车在断面载客量的推算，能够将问题构建成易于求解的线性规划问题。需要说明的是，高峰时段内乘客大都以通勤为目的，客流出行目的地相对稳定，此假设具有一定的合理性，类似假设在Gao等[8]，Wang等[9]研究中同样被使用。

假设2 在容量分配策略下，所有乘客都不会改变自己的出行计划，即不考虑乘客放弃出行，或反向绕行的情况。Meng等[10]在研究关于过饱和地铁线路协同客流控制方法时做出了同样的假设。

假设3 为方便将模型建立成线性整数规划模型，本文将连续的时间轴离散成若干微小的时间颗粒，采用集合T表示。

假设4 仅考虑一个方向上的列车容量分配。由于双向运行的地铁线路是在两个方向上分别为乘客提供运输服务，所以可以用同样的方法解决另一个方向上的容量分配计划。

2.2 模型约束条件

2.2.1 容量分配约束

实际运营中，预留过多的车厢数一方面会增加运营成本，同时也会增加乘客的等待时间。为了不过多增加车站内乘客的等待时间，对最大预留车厢数进行限制，即

式中：cl,s为列车l离开车站s时预留的车厢数量；cmax为可预留的最大车厢数；L为运营列车集合。

由于列车运营至终点站时，所有乘客均需下车，列车驶离终点站完成此次运营。因此，列车在终点站无需进行车厢预留，其对应的预留的车厢数应为0，即

实际运营过程中，预留车厢一旦被释放，其无法再次被预留用于后续的旅程。因此，列车的预留车厢数量应在整个旅程中不断减少，即

2.2.2 乘客运载约束

为清晰描述乘客在地铁系统中动态加载过程，构建相关的乘客运载约束。

列车到达车站时登上列车的乘客数主要由当前等待乘客数与剩余列车容量之间的最小值决定。

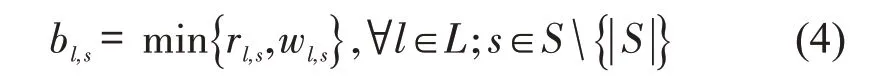
式中：bl,s为在车站s登上列车l的乘客数；wl,s为在s站等待列车l的乘客数；rl,s为列车l在s站的剩余容量。

在过饱和状态下，车站的等待乘客数量wl,s包括前一辆列车离开时遗留在站台的乘客数和当前列车出发前新到达的乘客数。对于首列车而言，等待登上列车的乘客数即为该列车出发前到达车站的累积人数。

式中：tl,s,d为列车l离开车站s的时刻；ps(t)为在t时刻到达车站s的客流数量；fl,s为列车l离开车站s时遗留的乘客数。

列车剩余容量主要由决策变量预留车厢数cl,s、列车l离开s-1 站时列车装载乘客数zl,s-1和在s站从列车l下车的人数al,s决定，即

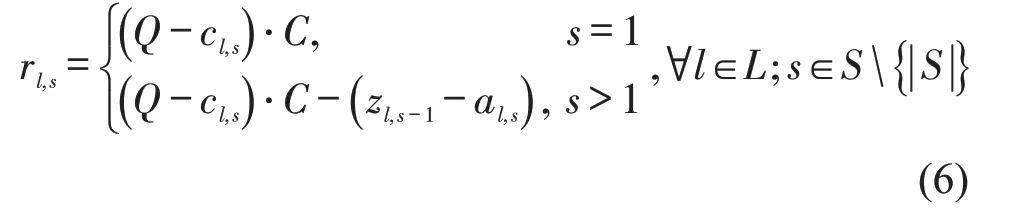
式中：Q为列车的编组数量；C为每节车厢的容量。

由于本文假设乘客在各车站s登上列车l的人数中，前往各目的站的比例固定，采用δm,s,l表示。则在车站s从列车l下车乘客数为

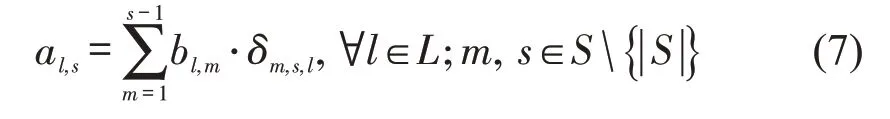
对于首列车而言，列车载离的乘客数量即为各车站上车乘客数，此为列车区间载客人数推算的起始点。后续区间的载客人数则可以通过列车离开上一个车站时装载的乘客数量、本站的下车乘客数量和上车乘客数量来进行推算，即

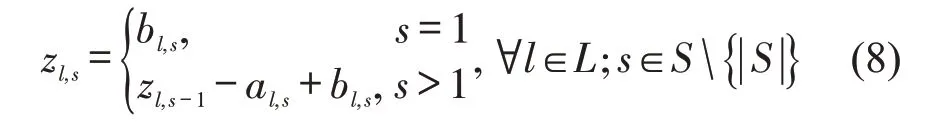
过饱和线路内列车经常无法运送完站台上所有等待乘客，部分等待乘客因无法登上列车而被遗留在站台，其值为等待乘客数与上车乘客数之差，即

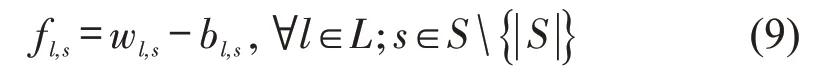
2.2.3 乘客聚集均衡性约束

本文通过容量分配策略，均衡各车站客流聚集，以提高线路整体安全性。因此，在本文的策略下，对各车站每趟列车的最大等待人数Mmax进行约束，以实现各车站聚集乘客数的均衡，以及服务公平性，即设置客流聚集约束为

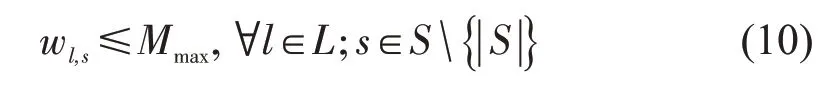
2.2.4 乘客的平均等待时间约束

车站s内等待乘客数的动态变化过程如图2所示。当服务列车到达s站时，列车内目的地为s站的乘客下车，同时车站内候车乘客登上列车，等待乘客数量下降。乘客的等待时间即为曲线所围成的不规则面积。为计算乘客的等待时间，可将连续的时间轴离散为若干间隔相等的时间点，采用T表示时间点集合。那么曲线所围成的不规则面积可近似等于图3 中 |T|个矩形面积之和，即近似为乘客的总等待时间。

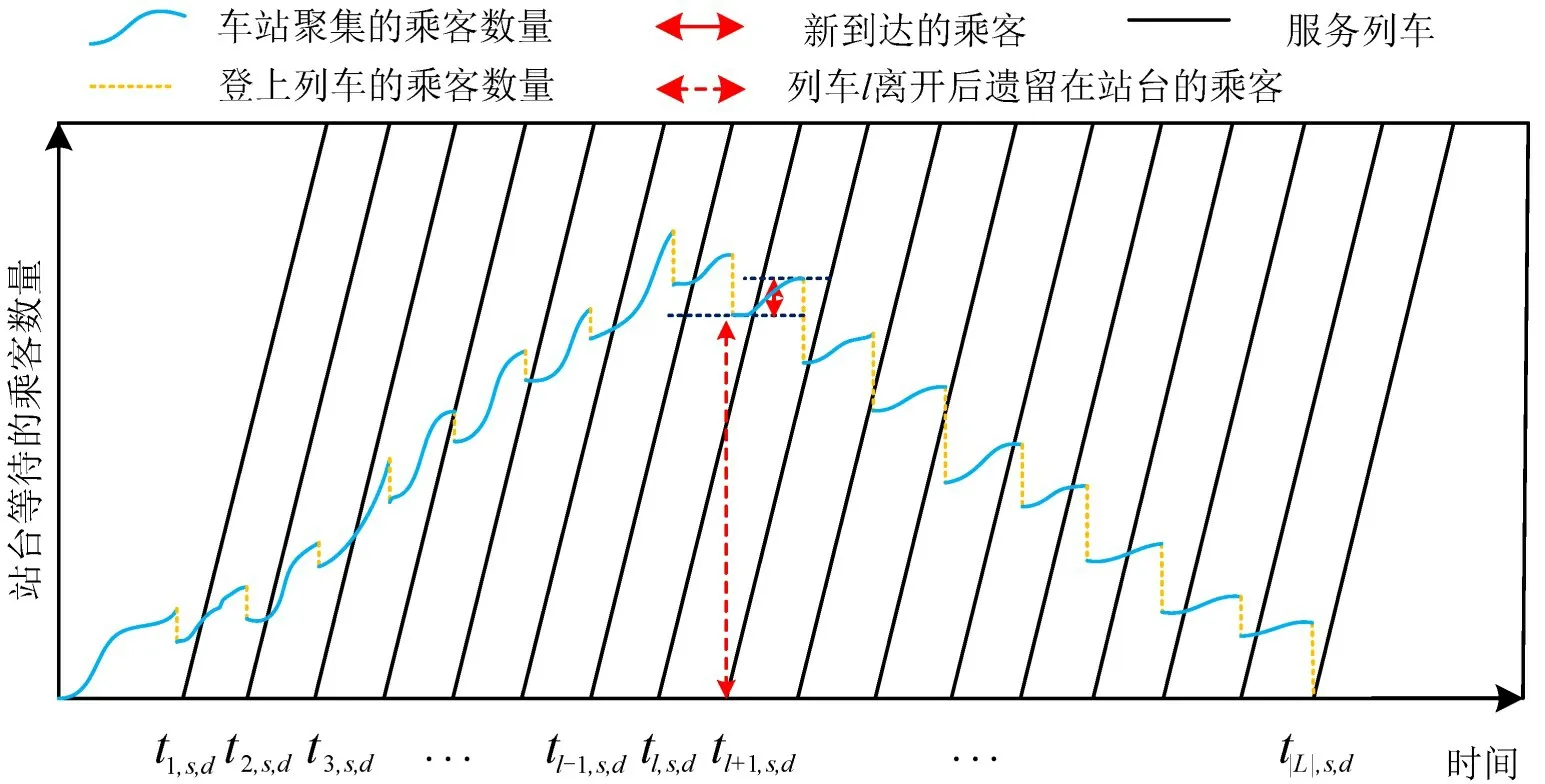
图2 车站s 内乘客等待时间说明图Fig.2 Iillustration of passenger waiting time at station s

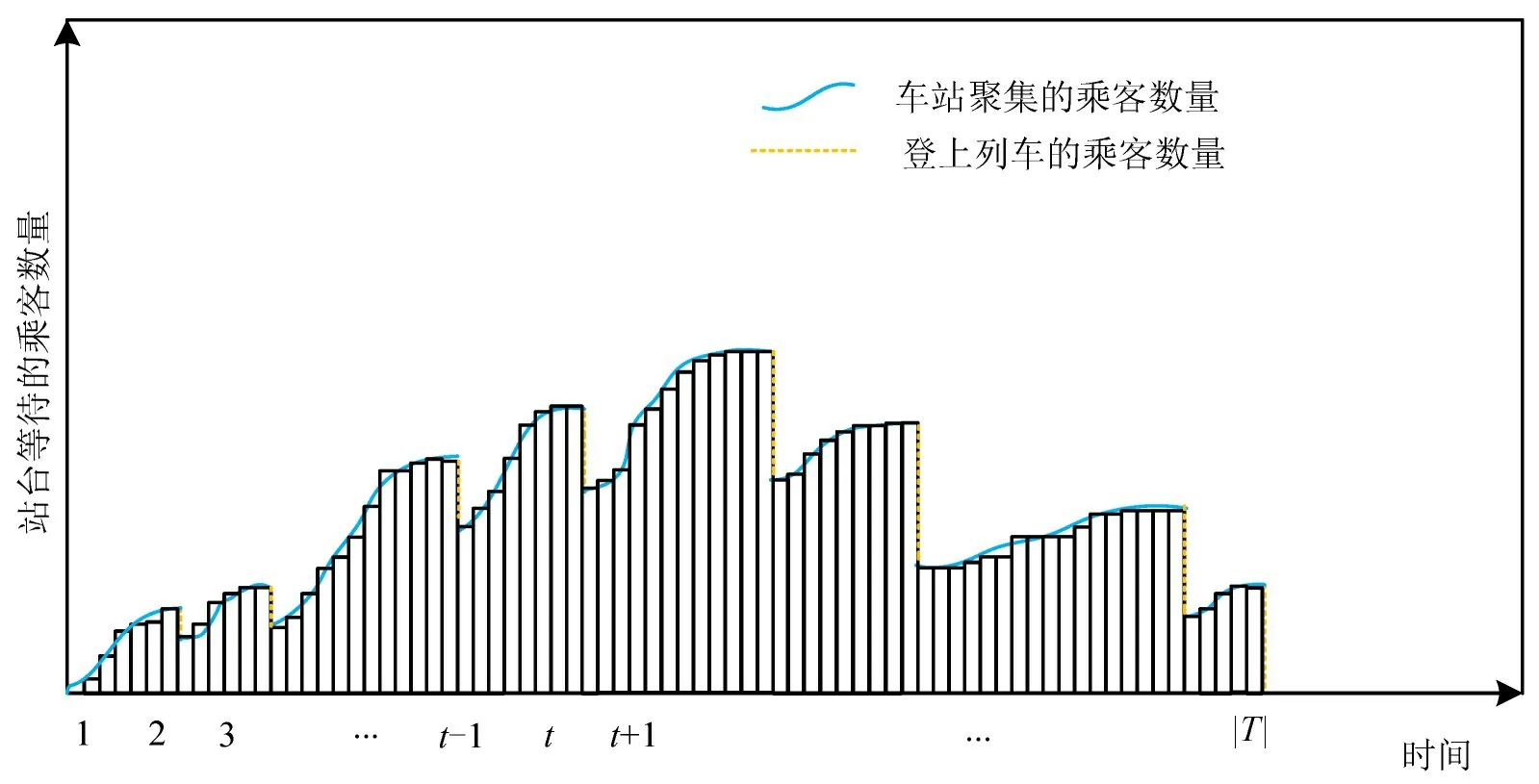
图3 时间范围离散化示意图Fig.3 Time range discretization diagram

引入二进制变量φl,s,t表示列车l在t时刻之前是否离开车站s，当列车l在t时刻前离开s站时φl,s,t的值为1，否则φl,s,t值为0。车站s在时间点t的等待乘客数ws(t)等于在t时刻之前所有累积到达的总乘客数和t时刻前各列车总登车人数之差，即

式中：ps(τ)为在时刻τ到达s站的乘客数量。

在车厢容量分配策略下，通过为拥堵车站分配一定的车厢容量，能够有效缓解车站拥堵，减少乘客等待时间，但同时也会增加部分上游客流的等待时间。为保证运输服务水平，对各车站的乘客平均等待时间进行约束，即

式中：Nmax为各车站乘客的最大平均等待时间。

2.3 线性化处理

尽管在上述过程中对考虑的问题施加了严格约束，但是其中约束式(3)为非线性约束，这使得所构建的模型无法采用传统的分支定界、分支割平面算法进行求解，也无法采用成熟的优化求解器(如CPLEX、GROUBI等)进行求解。因此，需对该约束进行线性化处理。首先，引入二进制变量ul,s表示rl,s与wl,s之间的大小关系，M为较大正数。其中，当rl,s≤wl,s时，ul,s的值为1；否则，ul,s的值为0。约束式(3)可以被等价线性化为

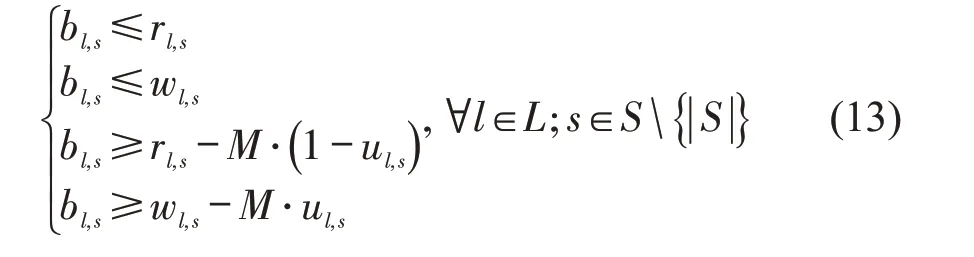
2.4 预留车厢优化模型

因非线性约束都已经线性化，故对过饱和地铁线路进行容量分配优化的模型最终可构建成线性整数规划模型为

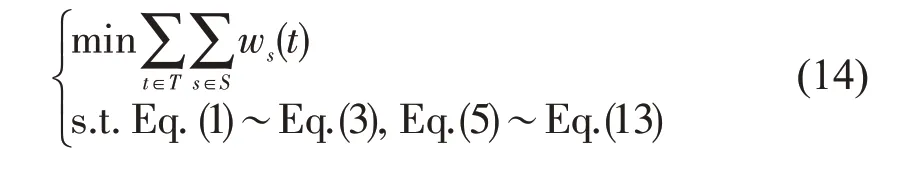
3 案例分析

3.1 基础数据

本文以2018年北京地铁八通线下行方向为例，共13 个车站，线路如图4所示。分析某工作日AFC数据，将其对应的客流量加载到本文所提出的模型中，并对其进行容量分配优化计算。研究时段为7:00-10:40，在此期间对所有运行的列车进行容量分配，该时段内共运行地铁列车53 列，7:00-9:00发车间隔为3 min，其他为4 min；离散时间间隔为1 min。

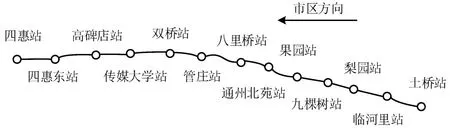
图4 北京地铁八通线线路示意图Fig.4 Schematic diagram of Beijing Metro Batong Line

考虑到高峰时段的超载情况，将车厢容量C设置为280 人·节-1，列车编组数量Q为6 节。车站的最大安全容纳人数Mmax为1500 人，乘客的最大平均等待时间Nmax为15 min，最大预留车厢的数量Cmax为3节。以下的实验均在1台AMD R7 2.90 GHz,16 G 内存，window 10 操作系统的计算机上进行，本文模型采用IBM CPLEX 12.3 优化器进行求解，计算终止条件为上下界Gap为0.5%。

3.2 计算结果与分析

首先，对不采取容量分配策略下的线路乘客聚集情况进行推算，结果如图5(a)所示。可以看出，在正常运营策略下，双桥和传媒大学站出现较为严重的客流聚集，特别是传媒大学站，最大等待客流数达到3642 人，车站客流极为拥堵。线路乘客的总等待时间为418027 min，传媒大学站的乘客平均等待时间达到31 min。

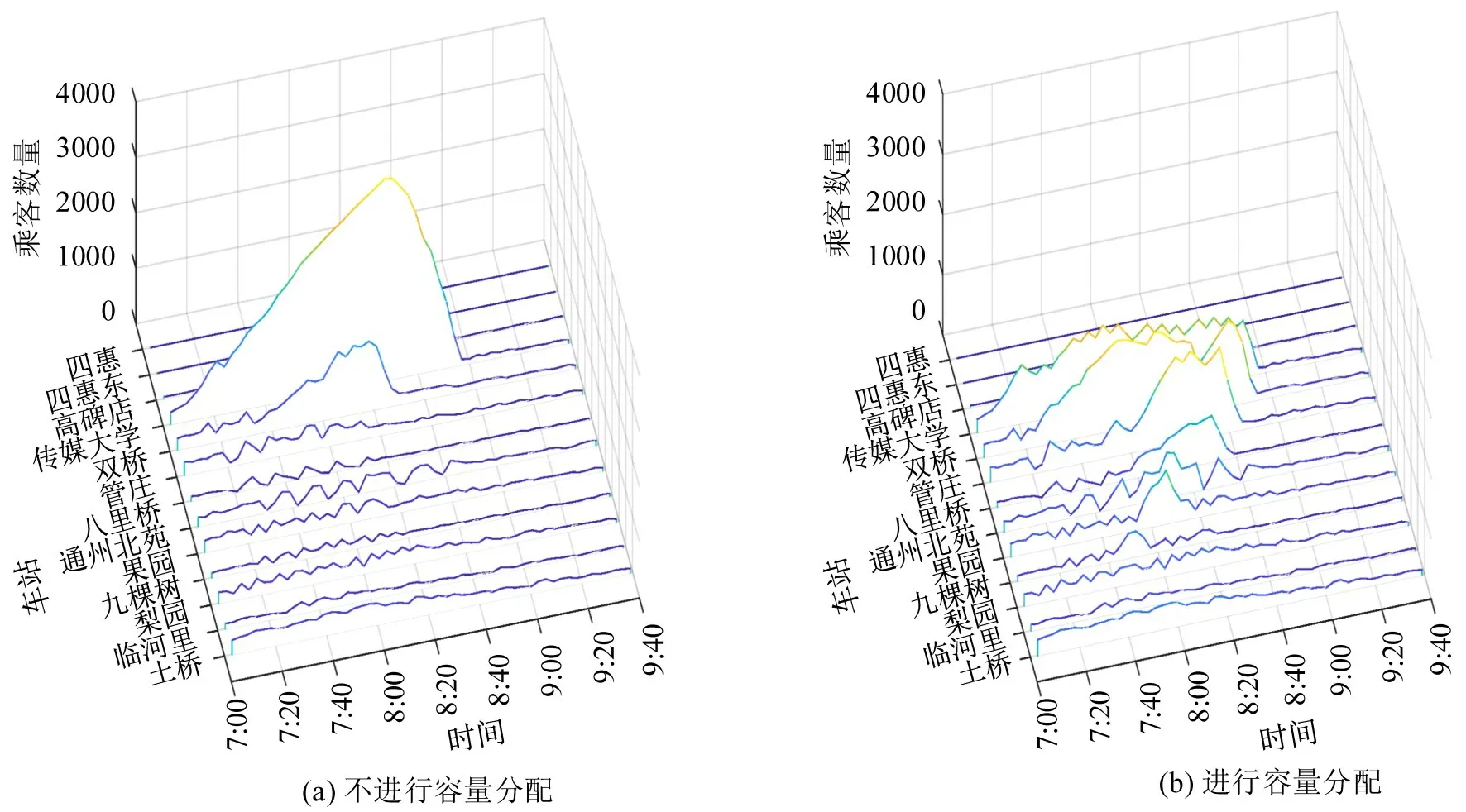
图5 对实际案例进行容量分配前后的乘客聚集情况Fig.5 Passenger accumulation at stations without capacity allocation for real-world case

采用容量分配模型进行优化求解，经过65 s计算，获得Gap 为0.5%的较优方案，如图6所示。由于求解结果中仅其中20 辆列车进行了容量分配，故仅给出20辆进行容量分配列车对应的容量分配方案。图6 的横坐标为案例中地铁线路的13 个车站，纵坐标为进行容量分配列车的发车时刻，矩形代表各列车经过各车站时列车容量分配的情况，其内部较小的矩形代表预留车厢的数量。例如，图6中第1 趟列车于7:24 从土桥站出发并预留1 节车厢，最终在传媒大学站释放预留车厢。从方案中可以看出，所求解方案很好地考虑了客流的时变特性，车厢的分配数在不同车站和列车中呈现变化特性。

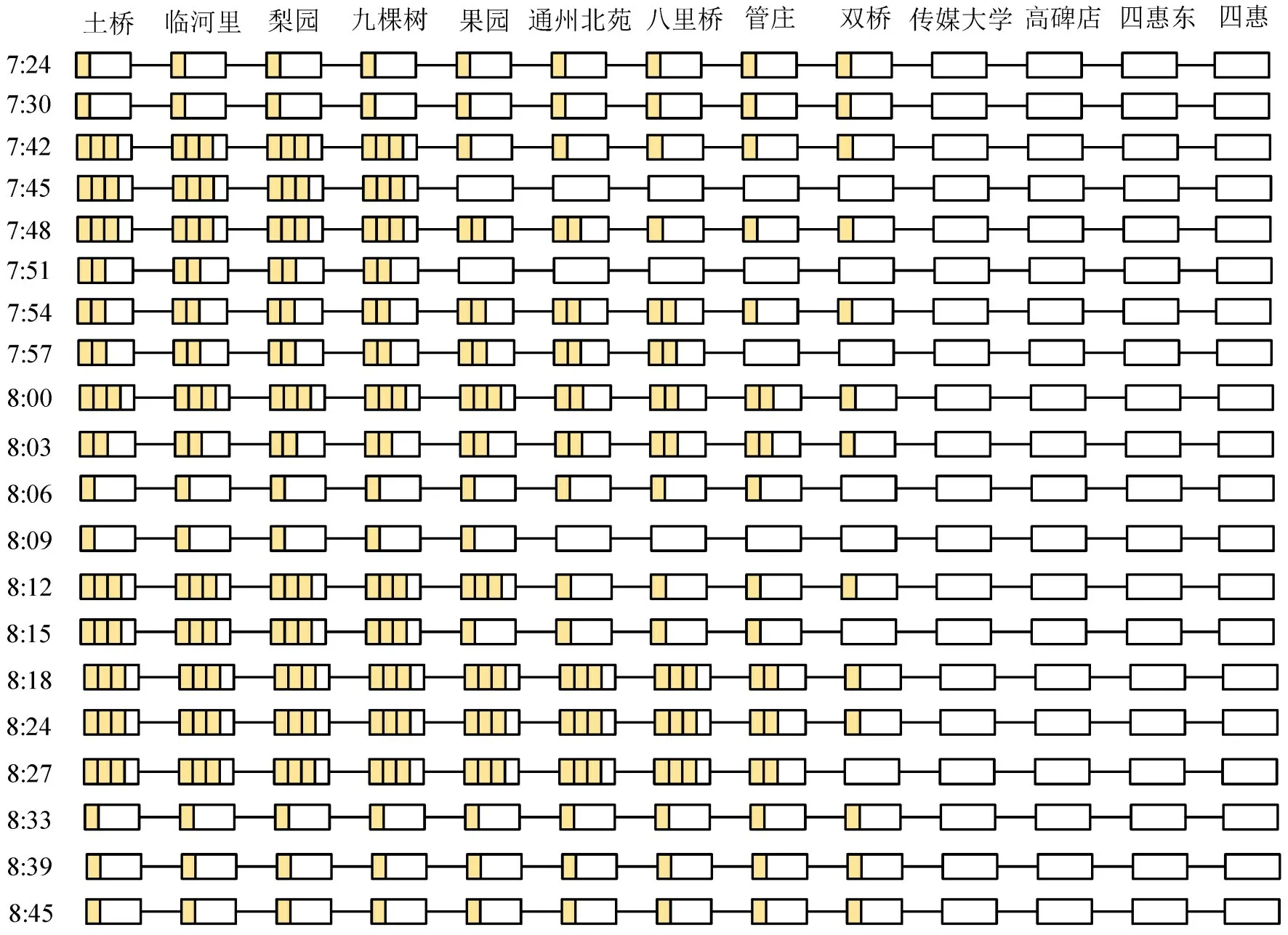
图6 实际案例的容量分配方案图Fig.6 Diagram of capacity allocation plan about actual case

为进一步分析容量分配策略的效果，将该策略下乘客在各车站的聚集情况展示在图5(b)中。对比发现，对过饱和线路进行容量分配优化后，传媒大学站的聚集乘客数量大幅降低，最大等待乘客数由3642人降低至1345人，约降低63%，车站的极度拥挤得到了有效缓解。此外，为下游拥挤车站预留车厢时，由于上游车站部分乘客无法照常登车，果园站、通州北苑站、八里桥站和管庄站等上游车站的聚集乘客数量有一定程度增加，但所有车站的聚集乘客数均小于1500 人。可以看出，容量分配方法很好地均衡了各车站客流聚集，达到了预先设想的提升运营安全性的目的。在容量分配策略下，列车经过管庄、双桥等车站时列车满载率明显下降，而在传媒大学和高碑店站列车满载率大致不变，证明拥堵车站内登上列车的乘客数量增加，容量分配策略有效分配列车运力并缓解拥堵情况。

在客运服务水平方面，容量分配策略下，乘客的总等待时间为420099 min，相对于正常运营情况下，仅增加了0.5%。同时，采取容量分配策略前后线路内各车站乘客平均等待时间如图7所示，其中在不采取容量分配策略的情况下，传媒大学站的乘客平均等待时间为31 min，显著高于其余车站的乘客平均等待时间。采取容量分配策略后，传媒大学站的乘客平均等待时间降低至15 min，约降低51%，并且线路内所有车站的乘客平均等待时间均小于15 min。可以看出，在容量分配策略下，拥堵车站的客运服务质量得到大幅提升，同时其余各站的客运服务水平也能得到较好保障，服务的公平性得到很好提升。

图7 采取容量分配策略前后乘客平均等待时间对比图Fig.7 Comparison chart of average waiting time of passengers with and without capacity allocation

3.3 不同最大等待乘客数的灵敏度分析

为分析不同的最大等待乘客数量下容量分配优化模型的表现，分别设定不同车站最大等待数阈值Mmax，其余基本参数保持不变，对提出的模型进行测试，计算结果如表1所示。实验结果表明，在不同最大等待乘客数量下，所提出模型均能计算出对应的较优容量分配方案。通过结果可以看出，随着Mmax的增加，乘客总等待时间不断减少。可见，随着对于安全阈值的放宽，乘客的等待时间能够在一定程度下降，但客流拥堵情况会随之变得恶劣。因此，在实际运营中需根据需要，设定合理的最大等待乘客数，从而在运营安全和服务质量间进行合理权衡。

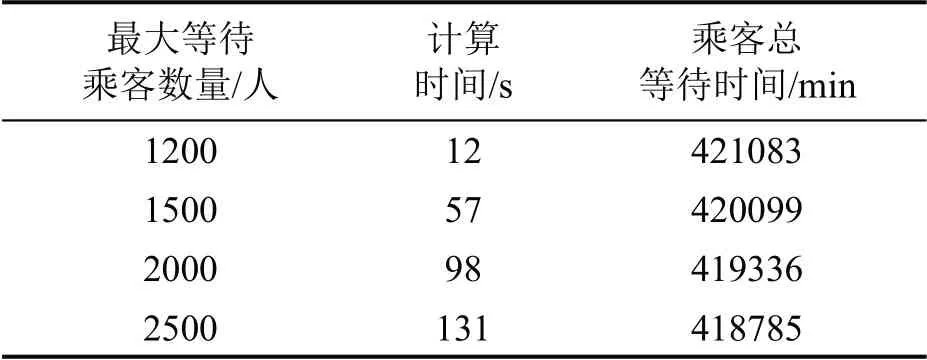
表1 不同最大等待乘客数量下的乘客总等待时间Table 1 Total waiting time of passengers under different maximum number of waiting passengers

3.4 不同最大预留车厢数的灵敏度分析

通过设置不同的最大预留车厢数Cmax分析其对容量分配模型结果的影响。其中，最大等待人数阈值参数随车厢数的增多而减少，其他参数保持不变，计算结果如表2所示。通过分析发现，随着最大预留车厢数量增加，乘客总等待时间和最大等待乘客数均不断降低。这说明随着可预留车厢数的增加，问题的优化空间得到提升，乘客等待时间和车站拥挤程度均能够进一步优化。但同时也可以看出，乘客等待时间的提升幅度会不断减少，车站内最大等待乘客数的降低幅度也不断减小。实际运营中，预留车厢数过多会给上游车站乘客的乘车带来极大不便，应根据实际情况设置合理的最大可预留车厢数。

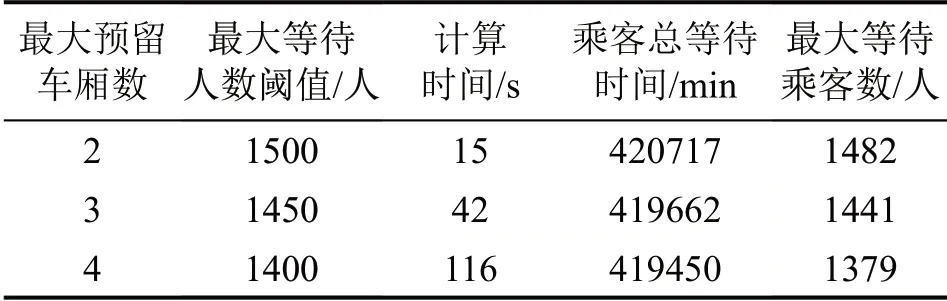
表2 不同最大预留车厢数量下的乘客总等待时间Table 2 Total waiting time of passengers under different maximum number of reserved carriages

3.5 不同最大平均等待时间的灵敏度分析

通过设置不同最大平均等待时间Nmax，分析其在不同取值情况下对容量分配优化模型计算结果所产生的影响，计算结果如表3所示。可以看出，随着Nmax取值增大，乘客总等待时间不断降低。这说明在更多牺牲上游车站乘客服务水平时，线路总体服务水平能够得到更好地提升。因此，在实际运营过程中，需根据客流情况设置适当的最大平均等待时间阈值，在牺牲上游车站服务水平和提升整体线路服务水平之间做出权衡。

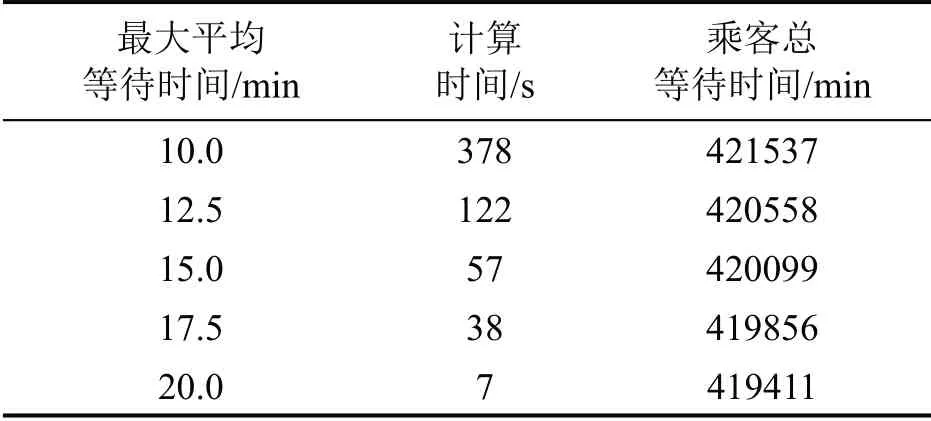
表3 不同最大平均等待时间下的乘客总等待时间Table 3 Total waiting time of passengers under different maximum number of average waiting time

4 结论

为缓解过饱和地铁线路中极度拥堵的情况，本文从安全角度出发，提出一种新颖的车厢容量分配方法协同控制各车站上车人数，建立该问题的线性整数规划模型。以北京八通线为例，对所提模型进行测试，实验结果表明：

(1)容量分配策略能够很好地均衡线路上各车站的客流聚集量，使极度拥堵车站的客流聚集量大幅下降，线路运营安全性得到很大程度地提高。

(2)在客运服务水平方面，容量分配策略下，乘客的总等待时间仅增加0.5%，同时所有车站的平均等待时间都能够控制在15 min内，各站服务水平均能得到较好保证。

(3)通过灵敏度分析发现，本文模型具有较好的稳定性，针对不同的最大等待乘客数阈值，均能生成较优的容量分配方案，研究成果能够为实际运营提供很好的参考。