引入价格窗的定制公交线路优化研究

岳昊，刘建业，李崇楠

(北京交通大学，综合交通运输大数据应用技术交通运输行业重点实验室，北京 100044)

0 引言

大力发展公共交通是我国城市交通领域的重要发展战略。为解决乘客出行需求多样化与公共交通服务单一化间的矛盾，重点发展多元化公共交通已成为城市交通发展的必然趋势。传统公共交通(固定运营线路、时间和票价)为体现其公益性和公平性，一般采用低票价机制；因此受其成本限制，很难为出行地点偏僻或出行时间特殊的乘客提供公交服务。定制公交是为有类似出发地、目的地、出行时间和服务水平的乘客提供一人一座、门到门的定制化快捷公交服务[1]；其票价通常高于传统公交票价，但低于自驾车和出租车的出行费用；可以有效解决传统公交线网未覆盖区域、运营时间外等特殊乘客的公交出行问题；在服务对象上与传统公共交通形成鲜明的互补关系，是多元化公共交通的重要组成部分。

定制公交运营模式最早起源于国外共享出行的理念。Kirby等[2]通过对定制公交案例分析，得出定制公交有利于提高公共交通使用率；Shaheen等[3]明确了定制公交运营的基本流程。国内定制公交发展起步较晚，2013年北京市和青岛市首次开通了定制公交线路[4]；徐康明等[5]探讨了定制公交服务的定义、服务要素、优势和适用性；Liu等[6]首次分析了定制公交在30 个中国城市的发展，重点介绍了定制公交的设计运营过程。

在定制公交理论研究方面，张敏捷等[7]提出以线网覆盖率最大、上座率最高、运营投入最少为目标的函数，考虑线路长度和上座率约束的定制公交线路规划模型，并采用改进蚁群算法求解；雷永巍等[8]构建了面向互联网定制公交，以最大需求服务率和最小费用为目标，以最大载客量和乘客时间阈值等为约束条件的动态网络调度模型，并设计了并行蚁群算法对模型进行求解；Tong等[9]建立了以不可达乘客数量最小为目标，考虑容量限制和时间窗等约束条件的规划模型，并采用拉格朗日松弛算法求解；陶浪等[10]建立了以乘客出行时间和车辆油耗最小为目标，考虑车辆容量限制、出行时间约束、出行费用约束的定制公交线路优化模型，并采用改进NSGA-Ⅱ算法求解；申婵等[11]构建了以乘客等车成本、乘客损失成本及车辆运行成本为目标函数，考虑流量和容量约束的定制公交线路优化模型，并采用禁忌搜索算法对问题进行求解；Lyu 等[12]构建了以运营商盈利最大为目标，考虑巴士公司总载客量约束的优化模型，并设计了启发式算法求解；陈汐等[13]构建多区域运营模式的通勤定制公交线路规划模型，以最小化乘客出行成本、车辆运营成本为优化目标，并设计两阶段启发式算法求解；Chen等[14]构建了以乘客的额外旅行时间最小和运营成本最小为目标函数，考虑分配约束、时间约束、容量约束、方向约束等条件的定制公交线路设计模型。

综上所述，目前研究主要关注于固定票价机制下的定制公交线路优化问题。然而，在实际的工程应用中，定制公交由于单一票制、服务人数、运营成本等原因造成实际载客率不足、线路延伸与覆盖率不够等“运营稳健性”问题，特别是由于载客率不足造成票款收入不能满足线路运营成本时，导致线路无法开通或停运。当某个区域不能提供传统公交或定制公交服务时，居民需要支付更高的出行成本(私家车、出租车等)实现出行。为解决定制公交的“运营稳健性”问题，本文提出定制公交的浮动票价机制，即乘客为实现公交出行，基于公交基础票价(按里程计价)提出自身可接受的支付范围；公交企业基于公益性和公平性的原则，根据线路的运营成本与乘客的支付意愿，在乘客可接受的支付范围内确定其最终票价。该机制在乘客可接受的支付范围内，通过部分乘客的额外支付来维持线路的运营成本，从而保证定制公交线路的开通和“稳健运营”，实现线路整体乘客的公交出行，避免出行成本更高的非公交出行。

在浮动票价机制的框架下，从公共交通公益性的角度出发，综合考虑乘客与公交企业之间的权衡关系，以保证企业运营成本与服务更多乘客为目标，研究定制公交的线路优化问题。首先，引入价格窗的概念描述乘客出行过程中可接受的支付范围；提出超额均摊的票价支付假设规则，使乘客在保证出行的基础上支付最少费用。其次，基于时空窗与价格窗的乘客出行需求特征构建定制公交线路优化模型，以企业运营成本最小和服务乘客数最大为目标函数，通过运营盈利约束保证企业的运营成本，联合优化乘客-车辆匹配和车辆路径两个子问题。最后，采用GAMS 软件进行建模和求解，并通过算例对模型进行验证。

1 问题描述

1.1 问题描述与输入输出

本文要解决的问题可描述为，每位乘客为实现定制公交出行，基于公交基础票价提出自身可接受的支付范围，形成一个票价可接受范围，定义为价格窗；同一辆车的乘客在自身可接受的支付范围内共同分担车辆的最低发车收入，实现更多乘客的公交出行；公交企业则根据乘客出行信息(时空窗和价格窗)进行乘客-车辆匹配和车辆路径优化，并基于票价支付假设规则计算乘客的最终支付票价，从而实现在保证企业运营成本的基础上服务更多乘客。

问题预先设定公交基础票价和最低发车收入。实际应用中，公交票价的制定与乘客的出行距离和出行时间相关；参考文献[15]，本文公交基础票价的定价方式采取按里程计价，20 km(含)以内5 元，每增加5 km(含)以内增加3 元。而最低发车收入通常与驾驶员工资、车辆油耗以及车辆损耗等相关，由企业根据企业的实际运营情况来计算确定。票价收入上界为乘客可接受支付的最大票价总和，下界为乘客公交基础票价总和。当票价收入上界超过最低发车收入时，线路发车；否则，不发车取消服务。表1描述了问题的主要输入和输出。

表1 定制公交线路优化问题的输入输出Table 1 Input and output for customized bus route optimization problem

1.2 时空窗与价格窗

给定一个由(N,M)表示的物理运输网络，其中，N为节点集合，M为有向弧的集合，点i,j∈N，弧(i,j)∈M。用(T,A)表示时空网，其中，T为时空点集合，A为时空弧的集合，点(i,t)∈V表示时刻t位于点i，时间维采用均匀离散时间间隔(如1 min)，弧(i,j,t,s)∈A表示时刻t从点i出发，时刻s到达点j的时空路径。

乘客出行规划问题中，一般采用时间窗概念表示乘客出行要求的时间范围，包括上车时间窗和下车时间窗。而时空窗是时间窗与空间约束相结合的一种约束，表示乘客出行要求的时间范围和地点范围，包括上车时空窗和下车时空窗，如乘客想要在t～s内从地点i出发，其上车时空窗可表示为[i,(t,s)]。

通常情况，选择定制公交出行的潜在乘客会综合衡量收入水平、准时性、便捷性、舒适性、出行目的、出行距离、出行意愿等多种因素，根据公交基础票价产生一个最大支付意愿。价格窗就是乘客基于公交基础票价所能接受的票价支付范围，下界是公交基础票价，由企业根据乘客OD间的最短路径距离计算确定，上界是乘客的最大支付意愿，由乘客自己确定。也就是说，若乘客可以得到公交服务，则其最终支付票价位于价格窗之间。如公交基础票价为5 元，乘客最大支付意愿为10 元，其价格窗表示为[5,10]。

1.3 票价支付假设规则

首先，乘客提前支付可接受的最大票价；其次，企业根据票价支付假设规则计算得到乘客支付的最终票价；最后，将未出行的票价或超出的票价退回给乘客。在浮动票价机制下，存在同一辆车的乘客基于公交基础票价去分配额外票价支付的问题，即最终票价的计算问题，基于公交公益性、保证企业运营成本以及在保证出行的基础上支付最少费用等原则，提出超额均摊的票价支付假设规则(所有乘客在支付各自基础票价的基础上，逐层均摊需要额外支付的票价)来计算乘客的最终支付票价。

Step 1 同一辆车上的n位乘客首先支付公交基础票价F，然后判断n位乘客支付的基础票价之和是否超过最低发车收入S，若满足条件，每位乘客最终支付的票价为F；否则，乘客还需支付补偿票价Bn，转到Step2。

Step 2 补偿票价Bn定义为最低发车收入S减去支付的基础票价总和再除乘客人数，即。计算Bn，判断n位乘客所能支付的最大票价bp是否超过F和Bn之和，若满足条件，n位乘客最终支付的票价为F和Bn之和；否则，乘客还需支付额外补偿票价Fn，转到Step3。

Step 3 额外补偿票价Fn定义为所有乘客所能支付的最大票价bp与基础票价F、额外补偿票价F1、…、额外补偿票价Fn-1差值中的最小值，即Fn=min[bp-F-…-Fn-1]。计算F1和Bn-1，F1对应的乘客b支付票价为bb。判断其余n-1 个bp是否超过F、F1和Bn-1之和，若满足条件，其余n-1位乘客最终支付的票价为F、F1和Bn-1之和；否则，转到Step4。其中，，。

Step 4 计算F2和Bn-2，F2对应的乘客c支付票价为bc。判断其余n-2 个bp是否超过F、F1、F2和Bn-2之和，若满足条件，其余n-2 位乘客最终支付的票价为F、F1、F2和Bn-2之和；否则，转到Step5。其中，。

Step(n+1)计算Fn-1和B1，Fn-1对应的乘客d支付票价为bd。此时最后1 位乘客最终支付的票价为F,F1,F2,…,Fn-1和B1之和。其中，。

计算流程如图1所示。为了理解超额均摊票价支付规则的计算流程，假设3 位乘客b、c、d被公交服务，其价格窗分别为[5,9]、[5,6]和[5,15]，最低发车收入S为20 元，根据支付规则进行计算。Step 1，由于3×5＜20，转到Step 2；Step 2，计算，转到Step 3；Step 3，计算F1=1，B2=1，乘客c最终支付票价6 元，由于9＞5+1+1 和15＞5+1+1，故乘客b和d最终支付票价7元。可以发现，在超额均摊的票价支付规则下，乘客b、c、d除了支付各自基础票价(5 元)外，乘客b、d(各自额外支付2 元)分别比乘客c(额外支付1 元)多支付了1 元，但3 位乘客实现了其出行目的，且3位乘客均在自己可接受的支付范围内支付了最少的票价，体现了公共交通的公益性。

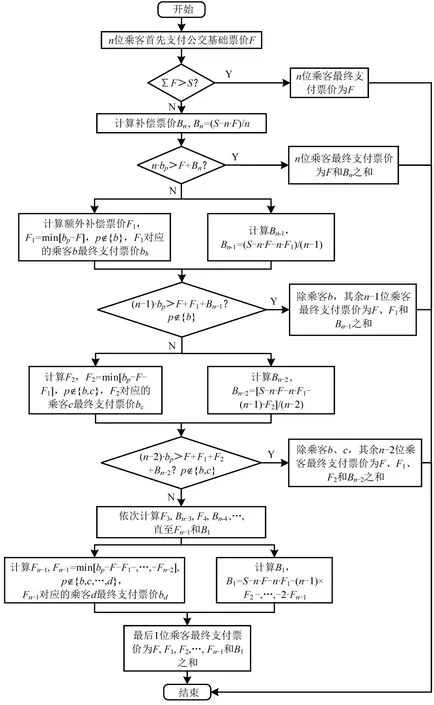
图1 票价支付的流程图Fig.1 Flow chart of fare payment

倘若，乘客b、d不替乘客c多支付这部分票价，则会出现下面这种情况：首先，乘客c将不能实现公交出行；其次，由于乘客b、d的最大支付意愿之和(21元)大于最低发车收入，乘客b、d仍然可以实现公交出行，但最低发车收入需要乘客b、d两个人承担，此时乘客b、d需要支付更高的公交票价，对乘客b、d来说更加不划算。因此，当高票价乘客需要为低票价乘客多支付一部分票价时，在一定程度上高票价乘客是愿意接受的，乘客间通过这种“抱团取暖”的方式来实现公交出行。

为了理解时空窗、价格窗和票价支付假设规则，以一个具有7 个节点和7 条无向边的小型物理网络为示例进行问题说明，如图2所示，边上的数字表示距离(单位为km)，行程时间(单位为min)的数值取距离的2倍。3位乘客想要出行，其中乘客b出行地点相对偏远，因打车难，打车成本相对会高一些；乘客c、d需要前往火车站，需要在凌晨出发，出行时间较严苛，超出传统公交的运营时间。为便于计算及问题说明，做出如下假设：定制公交的最低发车收入直接根据车辆的最大行驶里程设定为11元；乘客的公交基础票价与OD间距离数值相等；最大支付意愿取公交基础票价的2 倍；乘客打车成本按北京市出租车的收费方式计算；乘客相关出行信息如表2所示。以乘客b为例，乘客b的OD间距离为6 km，公交基础票价为6元，最大支付意愿为12 元，价格窗即为[6,12]，需要在(2,5)或(2,6)上车，在(3,15)或(3,16)下车。公交企业如果可以设计出满足最低发车收入的定制公交服务，则会满足乘客b的公交出行；否则，企业将不会对其开展服务，乘客可能需要采取非公交(自驾车或出租车)出行。

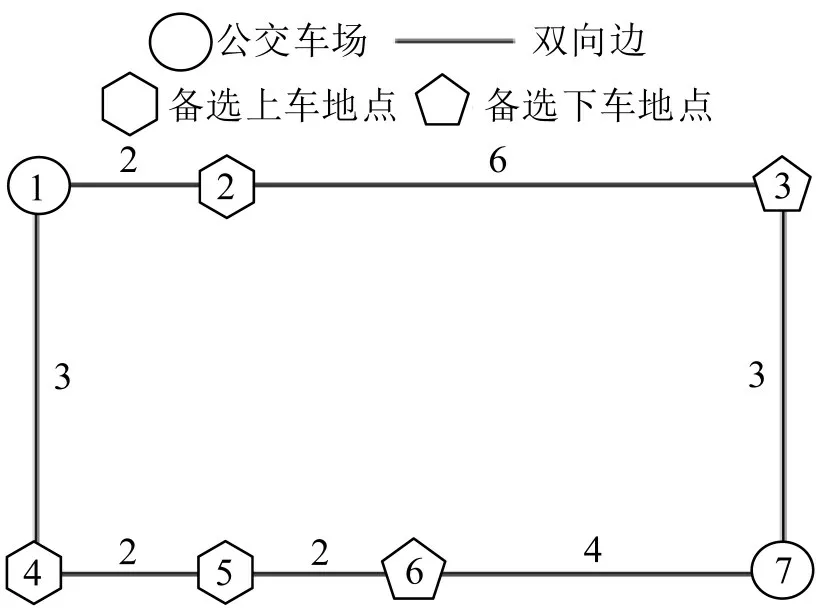
图2 小型物理网络示例图Fig.2 Example diagram of a small physical network

根据给定的乘客价格窗、时空窗和票价支付规则，图3 给出了示例的一个最优运输方案，其中公交车辆1 和2 的路径用时空点序列可分别表示为[(1,0),(4,6),(5,10),(6,14),(7,22)]和[(1,0),(2,4),(3,16),(7,22)]。所有乘客都在各自给定的价格窗和时空窗内被接送，其中，乘客c、d被车辆1运送，最终支付票价分别为7元和4元；乘客b被车辆2运送，最终支付票价11元。

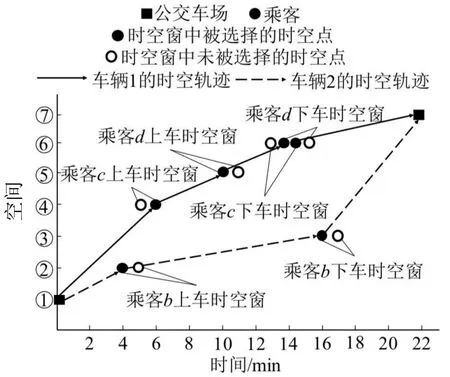
图3 示例时空网络下的车辆运输方案Fig.3 Vehicle routing scheme in a time-space network for illustrative example

可以发现，若采用固定票价机制，乘客b的公交基础票价(6元)以及乘客c、d公交基础票价的之和(6元)均小于车辆的最低发车收入(11元)，他们将不能被公交所服务。此时，乘客有两种选择，一是取消出行，不能实现其出行目的；二是采取非公交出行，但其打车成本(表2)远远大于公交出行费用。而引入浮动票价机制后，乘客b虽然在公交基础票价(6元)的基础上多支付了5元，但实现了其出行目的，且公交出行的最终票价在自己可接受的支付范围内，远小于采取非公交出行的费用(21 元)；乘客c、d通过共同承担额外的票价(5元)实现公交出行，虽然乘客c(承担3元)比乘客d(承担2元)多承担了1 元，但两位乘客均实现了出行目的，且他们的最终支付票价均在自己可接受的支付范围内，远小于非公交出行的费用(17 元和14 元)。在浮动票价机制的框架下，基于超额均摊的票价支付假设规则，通过高票价乘客为低票价乘客的多支付维持线路的运营成本，从而保证定制公交线路的开通和“稳健运营”；通过乘客间“抱团取暖”的方式，实现整体乘客的公交出行，避免出行成本更高的非公交出行，使乘客在保证出行的基础上支付最少费用。

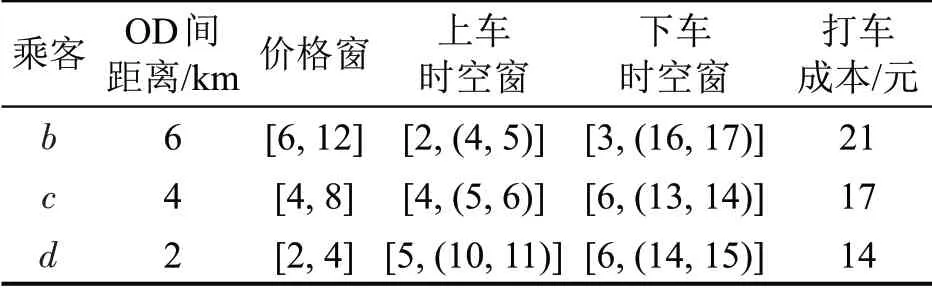
表2 乘客出行相关信息Table 2 Information about passenger travel

2 模型

2.1 符号说明

本文用到的符号及相关定义如表3所示。

表3 符号说明Table 3 Symbol description

2.2 模型构建

公共交通服务涉及两个标准，即乘客可达性和公交企业的运营成本。因此，本文建立整数线性规划模型，设立目标函数同时考虑企业运营成本最小和服务乘客数最大两个目标，目的是在满足最低发车收入的条件下，避免运力浪费，尽可能服务更多的乘客并提高企业的运营收入。

惩罚变量cp,v用来表示乘客p是否被分配给定制公交车辆。如果乘客p被分配给定制公交车辆VR，cp,v=0，即表示乘客p可以乘坐定制公交出行；如果乘客p被分配给虚拟公交车辆VV(除定制公交之外的出行方式，如出租车、自驾车等)，cp,v=1，即表示乘客p不能乘坐定制公交出行，需要采取其他方式出行。运输成本Ca表示车辆选择时空弧a要支付的相关运输成本，权重系数w表示失去候选客户和运输成本之间的权衡。

(1)目标函数

为更好地构建模型，将服务乘客数最大转换为未被服务乘客数最小，故目标函数为企业运营成本最小和未被服务乘客数量最小，即

(2)约束条件

①分配约束

确保1位乘客只被分配给1辆公交车辆。

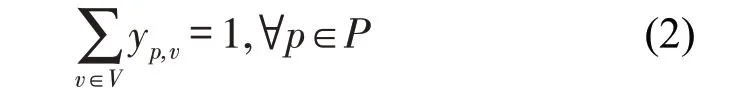
②惩罚约束

保证如果乘客p被分配给定制公交车辆，cp,v=0；如果乘客p被分配给虚拟公交车辆，cp,v=1。

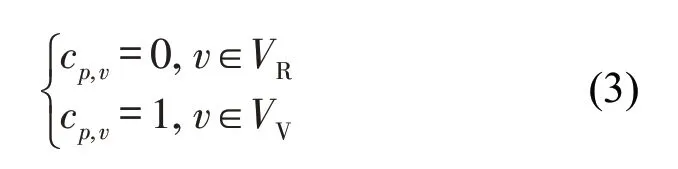
③容量约束

保证一辆定制公交车辆服务的乘客数不能超过其座位数，保证每个乘客都有一个座位，即

④运营盈利约束

为保证企业的运营成本，每辆公交车辆所载乘客能够支付的最大票价之和需要超过设定的最低发车收入，即

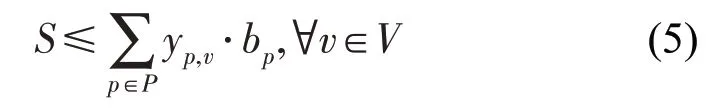
⑤时空窗约束

关联两个决策变量xa,v和yp,v，只有同时满足乘客p的上车时空窗与下车时空窗条件，定制公交车辆才能为乘客p服务。

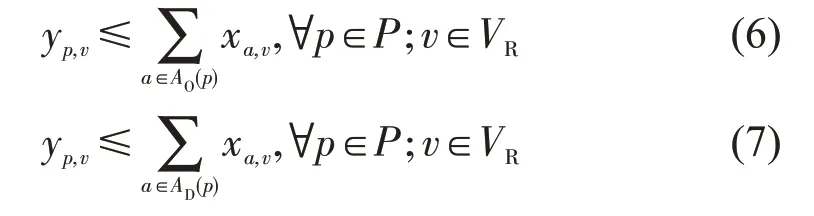
⑥流平衡约束

确保每辆公交车在开始时(即ev时刻)离开原点ov，在结束时(即lv时刻)到达目的地dv的约束为

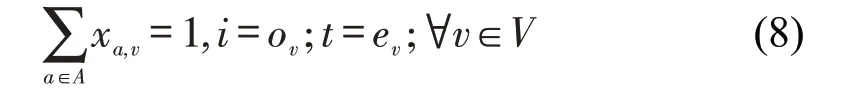
保证其他中间节点上流量平衡的约束为

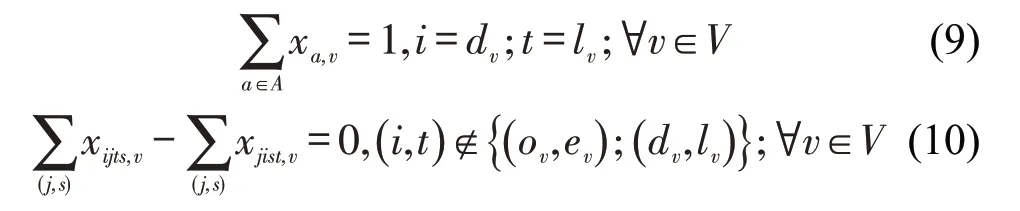
⑦二元约束

保证变量xa,v和yp,v取值为0或1的约束为

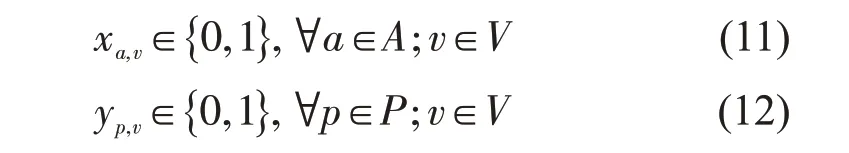
本文基于公交的公益性，在保证运营成本最小的基础上服务更多的乘客。服务更多的乘客通过目标函数来实现，而保证运营成本通过“运营盈利约束”来实现。可以发现，当所有乘客的价格窗上界等于下界时，此时本文模型与文献[9]的模型相同。但由于乘客在票价支付意愿上的差异性，乘客价格窗会存在一定差异性，因此相较于文献[9]的模型，本文提出的模型可以放宽最优解的搜索范围，在保证企业运营成本的基础上，基于乘客支付意愿，增加乘客可以乘坐定制公交出行的可能，从而对定制公交的运营方案、服务乘客人数、票价收入等产生影响。

模型基于价格窗，通过式(5)放宽最优解的搜索范围。模型的不同可行解，所对应的目标函数值不同，其最终票价收入也不同，从而在目标函数和最终票价收入之间建立了一个隐性对应关系。由于最终票价收入是在具体的可行方案下，基于价格窗和超额均摊票价支付规则计算得到，难以用显性公式所描述。因此，尽管目标函数中没有体现票价和票价收入，但可通过票价收入与目标函数的隐性对应关系求出最优解下的票价收入。未来的研究方向之一是将票价及票价收入引入到目标函数中。

3 算例分析

3.1 数据说明

本文基于文献[9]中的数据对构建的模型进行验证。该数据以Sioux Falls 网络上20 个乘客的通勤请求为示例，其中，该网络具有24个节点和38条无向边，边上的数字表示距离(单位为km)，假设行程时间(单位为min)的数值与距离相等，其他节点信息如图4所示。公交座位数为10。由于乘客上班时间一般是固定的，因此本文假设乘客最晚到达目的地的时间为第30 min或60 min，同时假设乘客可以接受提前5 min 内到达目的地，由此得到乘客的下车时空窗，然后根据OD间最短路径距离计算乘客的上车时空窗。20 位乘客的最短OD 距离均小于20 km，根据公交基础票价计算公式，计算得到20 位乘客的公交基础票价均为5 元，如表4所示。同时为了突出浮动票价的特征，以及模型间的可比性，将最低发车收入设定为30 元；Ca设定为0.01；w设定为1。另外随机生成若干个服从正态分布N(5,5)的整数，取20个超过均值5的整数依次表示20位乘客的最大支付意愿，得到乘客的价格窗。表4为20位乘客通勤需求所对应的价格窗和时空窗。

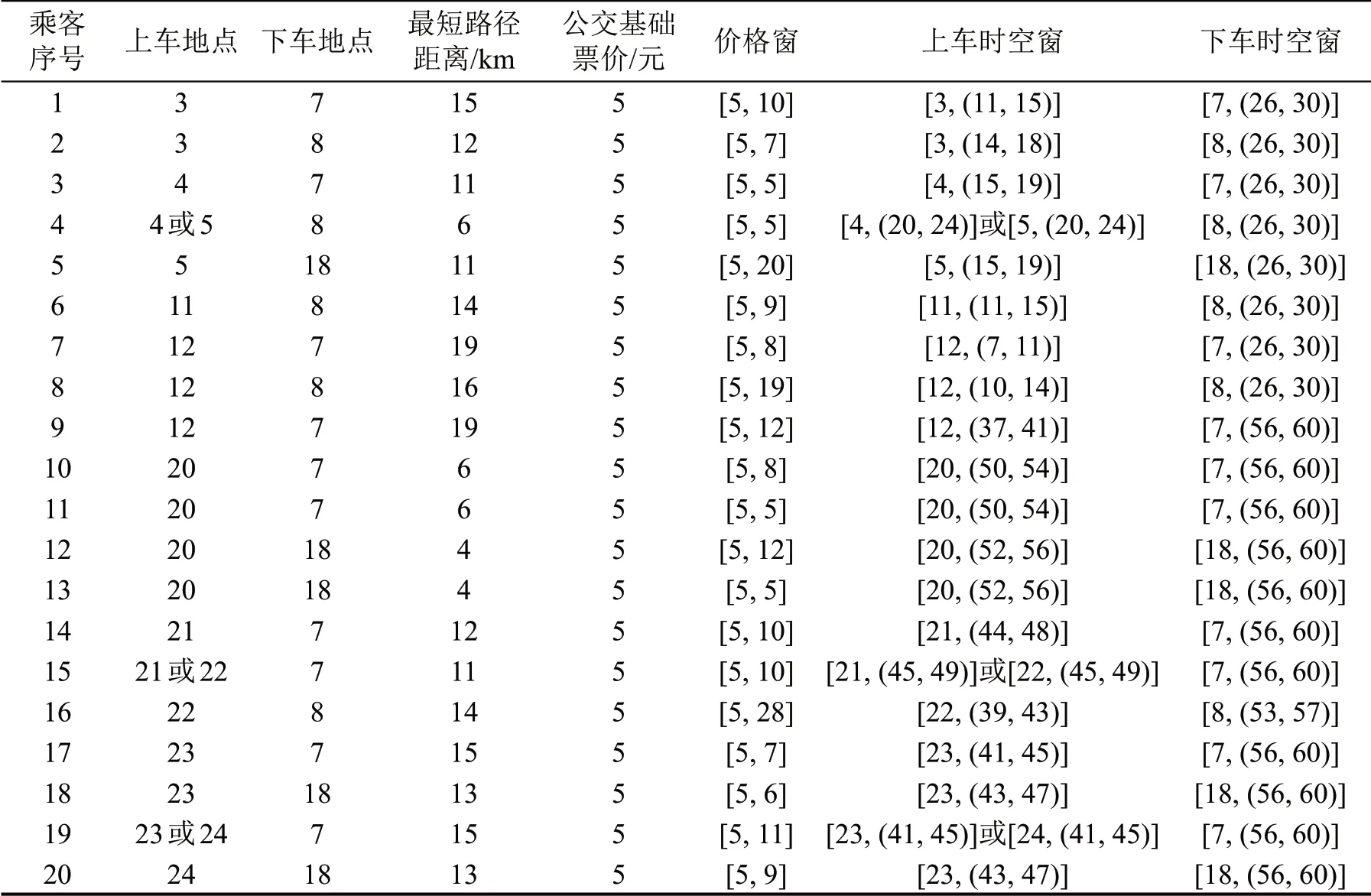
表4 乘客的通勤需求Table 4 Commuting needs of passengers

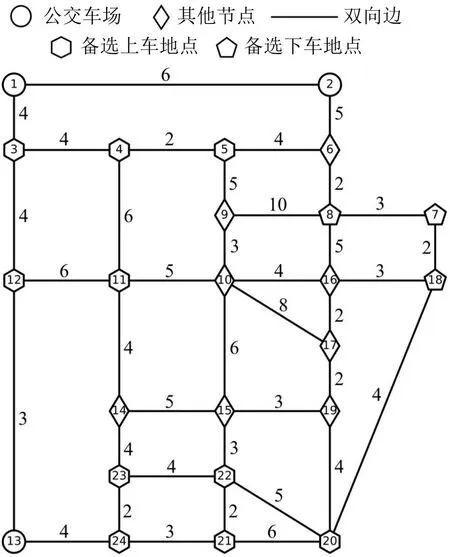
图4 简化的Sioux Falls网络Fig.4 Simplified Sioux Falls network

3.2 算例求解

本文建立的数学模型是一个整数线性规划模型，运用通用代数建模系统(GAMS)进行建模和求解。定制公交的最大运用车辆数等于所有乘客所能支付的最大票价之和除以最低发车收入；由于虚拟公交车辆可以看作是除定制公交之外的出行方式(如出租车、私家车等)，不需要进行乘客-车辆分配，因此不管是1位还是n位乘客，均可以被“1辆”虚拟公交车辆服务。20 位乘客所能支付的最大票价之和为206 元，最低发车收入为30 元，因此对算例进行求解时，初始定制公交的运用车辆数设为7，虚拟公交的运用车辆数设为1。算例最终求解时间为1.781 s，求解速度较快。计算结果表明，仅有2位乘客没有通过定制公交运送，18位乘客可以通过定制公交运送，共使用4 辆定制公交，其中，有4 位乘客通过车辆1 运送，3 位乘客通过车辆2 运送，6位乘客通过车辆3 运送，另外5 位乘客通过车辆4运送。公交车辆1～4 的路径时空点序列可分别表示为[(1,2),(3,6),(12,10),(3,14),(4,18),(5,20),(6,24),(8,26),(7,29)]、[(1,8),(3,12),(4,16),(5,18),(6,22),(8,24),(7,27),(18,29)]、[(13,37),(24,41),(23,43),(22,47),(20,52),(18,56),(7,58)]和[(13,35),(12,38),(13,41),(24,45),(21,48),(20,54),(18,58)]。表5 为乘客最终支付的票价以及上下车的时间和地点。定制公交的行驶路径如图5所示。

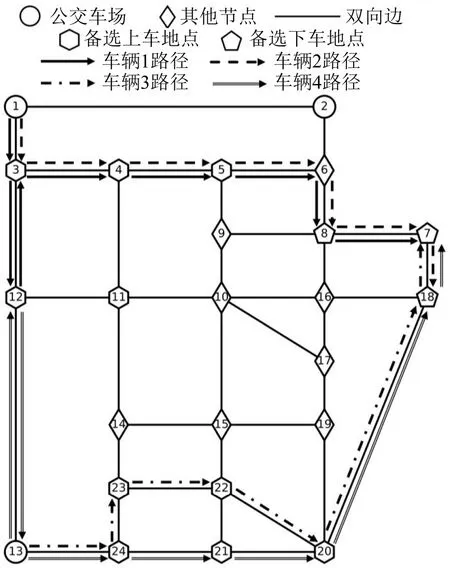
图5 定制公交的行驶路径Fig.5 Driving routes of customized buses

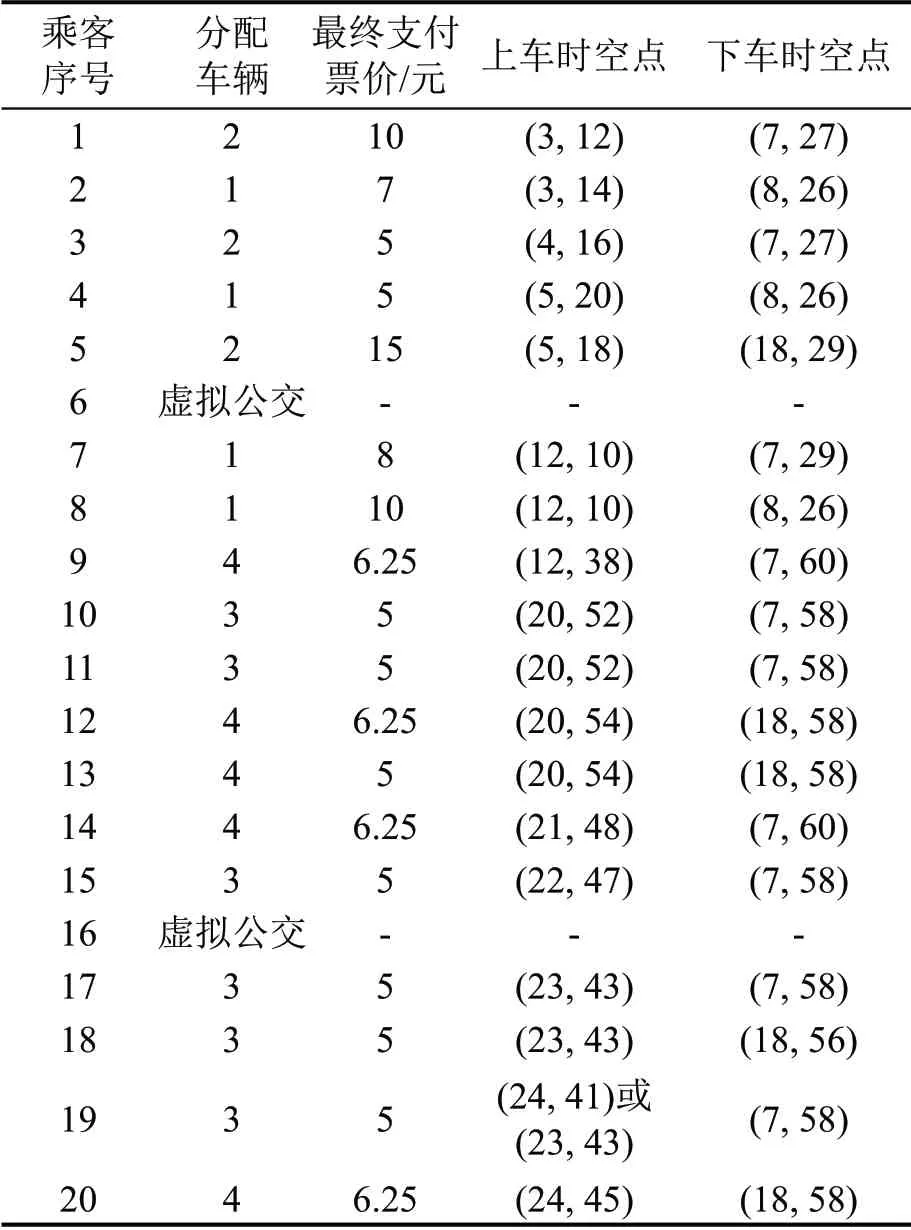
表5 乘客最终支付票价及上下车信息Table 5 Final fare paid by passenger and information about pick-up and drop-off

3.3 灵敏度分析

进一步在图3 简化的Sioux Falls 网络上分析价格窗和时间窗对目标函数的影响。在表3 信息基础上调整乘客的价格窗和时间窗以进行灵敏度分析。

(1)价格窗的影响

如前文所述，价格窗下界为车辆基础票价，由公交企业制定，在较长一段时间内(如1年)不改变，故通过调整上界来分析价格窗的影响。具体来讲，调高或降低上界若干个价格单位(如1元人民币)来体现价格窗上界的增幅。当通过调整上界的增幅使上界小于下界时，人为将上界取值改为下界。例如有两个价格窗分别为[5,10]和[5,7]，增加1 个价格单位，两个价格窗变为[5,11]和[5,8]；减少4个价格单位，两个价格窗变为[5,6]和[5,5]。价格窗上界不同增幅下的求解结果如表6所示。

通过对比分析表6 中价格窗上界不同增幅对求解结果的影响可知，价格窗可以反映出乘客出行过程的支付意愿。结果表明：一是当价格窗上界较大时，更多的乘客可以得到服务，而当价格窗上界较小时，将有许多乘客不能得到服务；二是乘客最终支付的票价总和，即企业的运营收入随未被服务乘客数的减少而增加。

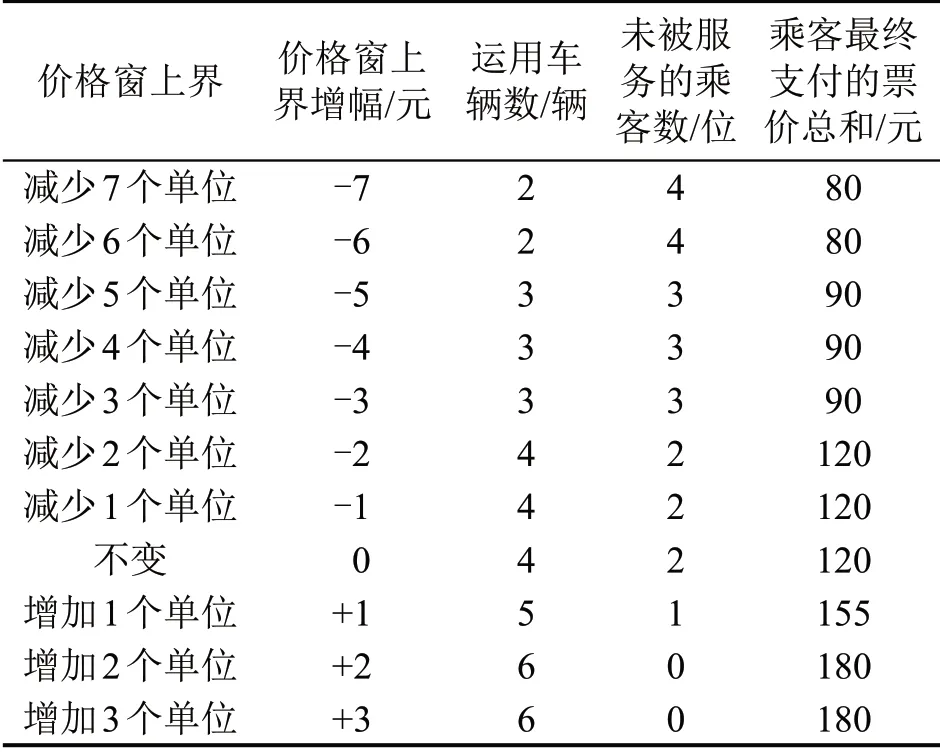
表6 价格窗上界不同增幅下的求解结果Table 6 Solution results under different increases in upper bounds of price window

(2)时间窗的影响

由于乘客通勤需求假定最晚到达目的地的时间是固定的，即时间窗上界(右端点)不变，故通过降低下界来调整其宽度从而分析时间窗的影响。为了对比引入价格窗的效果，本文分别在浮动票价机

制和固定票价机制两种情况下，在原乘客时间窗的基础上增加或减少下界若干个时间单位(如1 min)来改变时间窗宽度。时间窗不同宽度下的求解结果如表7所示。

通过对比分析表7 中时间窗不同宽度对求解结果的影响可知，时间窗可以反映乘客出行行为的灵活性。结果表明：一是当时间窗较宽松时，乘客出行的约束较松弛，更多的乘客可以得到服务，企业的运营收入进而增加；而当时间窗较紧时，乘客出行的约束较严格，许多乘客不能得到服务，企业的运营收入进而减少。二是在同样的场景下，相较于采用固定票价机制，引入浮动票价机制可以使更多的乘客得到服务，进而增加企业的运营收入，起到一个“杠杆”的撬动作用；可以在定制公交线路运营初期稳定客流，维持线路的开行，起到培育新线路的作用；在城市的发展扩张过程中，可以作为传统公交线路的培育手段。

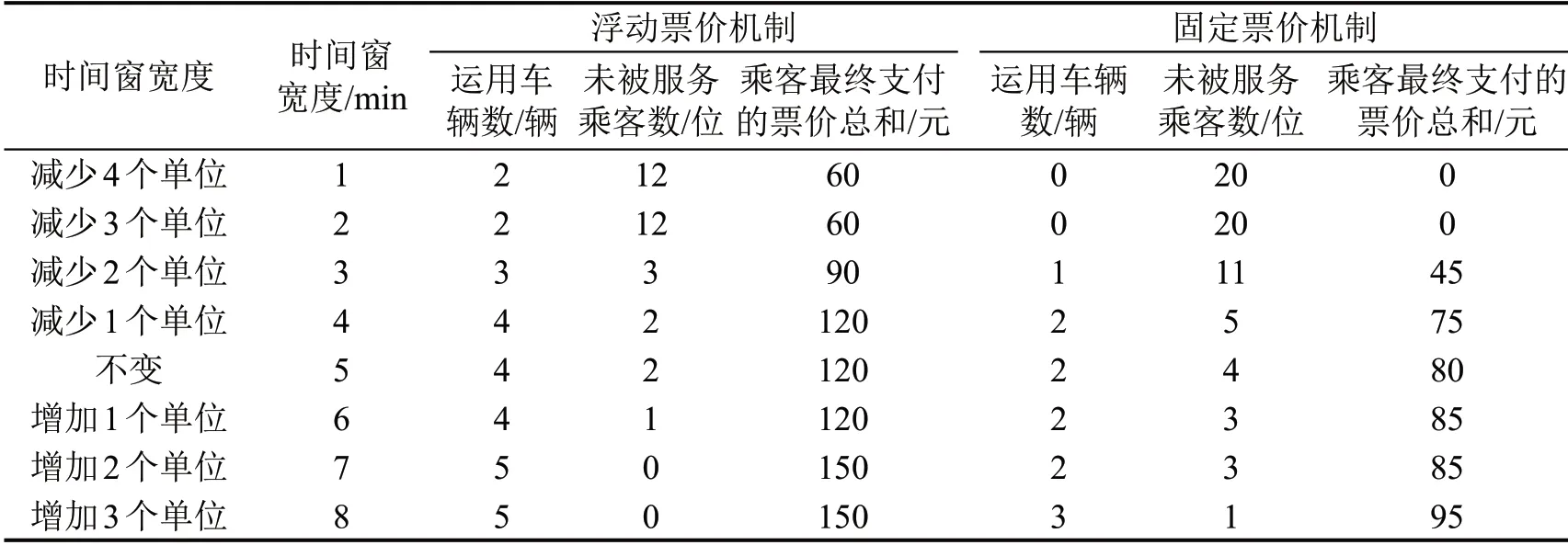
表7 时间窗不同宽度下的求解结果Table 7 Solution results under different widths of time window

4 结论

针对定制公交固定票价机制带来的服务乘客量少和运营收入低的问题，本文引入浮动票价机制，并提出价格窗的概念和超额均摊的票价支付假设规则，构建整数线性规划模型，综合考虑企业运营成本和服务乘客数两个方面。同时采用GAMS求解该模型并利用算例进行验证，分别对价格窗和时间窗进行灵敏度分析，相应给出定制公交的未服务乘客数和运营收入，并与采用固定票价机制进行对比，结果表明：(1)在价格窗上界一定的增幅内，所服务乘客数和企业运营收入随价格窗上界增幅的扩大而增加；(2)在时间窗一定的宽度下，所服务乘客数和企业的运营收入随时间窗宽度的增加而增加；(3)在同样的场景下，相较于采用固定票价机制，引入浮动票价机制可以松弛乘客的出行约束，服务更多的乘客，进而提高企业的运营收入。