考虑负效应最小化的电动汽车补能诱导研究

葛显龙，李婷，王博，尹作发

(重庆交通大学，a.经济与管理学院；b.智能物流网络重庆市重点实验室；c.交通运输学院，重庆 400074)

0 引言

2021年10月26日，国务院印发了关于《2030年前碳达峰行动方案》[1]的通知，并大力推广新能源汽车，逐步降低传统燃油汽车在新车产销和汽车保有量中的占比。相关数据[2]显示，截至2021年6月，我国纯电动汽车保有量为493万辆，占新能源汽车总量的81.7%，电动汽车作为新能源汽车的主力军，其规模化普及已成为一种必然趋势。但是，电动汽车的电池容量有限，为避免影响正常出行，需频繁到充电站进行补能，且补能时间较长。由于目前城市充电站发展速度落后于电动汽车增长量，且交通网络中充电桩与补能需求存在时空错配的现象，路网中大规模的补能行为不仅增加了驾驶员的行程时间和补能成本，而且易造成局部充电站拥堵，甚至影响交通，造成交通堵塞[3]。结合道路路网信息、充电站服务信息以及电动汽车补能信息，采取有效的补能诱导策略，减少电动汽车补能导致的一系列负面效应，对推动电动汽车行业发展具有重要意义。

目前，国内外学者对电动汽车充电诱导的研究主要集中在最短路线优化调度和网络均衡上，鲜有文献从补能负效应最小化的角度研究补能诱导问题，建立补能车辆与补能站的诱导方案。例如，任丽娜等[4]从驾驶员的角度出发，考虑了地形对能耗的影响以及电池的电量约束，提出以驾驶员的时间成本与经济成本之和最小为优化目标，为驾驶员规划充电路径。邢强等[5]提出将电动汽车、配电网与交通网这3方面交互作为一个整体进行研究，基于道路阻抗和Dijkstra最短路径算法为电动汽车推荐合理的充电站和路径。LIU等[6]表示纯电动汽车司机在选择路线时，不仅要尽量降低出行成本，还要考虑路线的可行性，并提出了相应的用户均衡条件描述电动汽车驾驶员的路线选择行为。闫云娟等[7]考虑电动汽车与燃油车混行的路网上，电动汽车的随机充电行为、充电站的排队等待时间以及最短路径的选择建立了混合用户均衡模型。李浩等[8]研究充电排队时间对电动汽车驾驶员选择路径以及路网均衡的影响，构建了相应的混合交通路网模型。

电动汽车在低荷电状态下的续航里程较短，因此，驾驶员的里程焦虑也是电动汽车补能行为的负效应之一。FRIEDRICH[9]将里程焦虑作为电动汽车与其他车辆相比固有的区别，被学者们广泛认可。HU等[10]提出为了避免里程焦虑，电动汽车司机往往会在电池荷电状态较高的情况下进行充电。邵赛等[11]将里程焦虑引入充电站选址问题中，基于里程焦虑和充电排队时间，建立用户效用最大化的充电站选址模型。虽然上述学者对里程焦虑进行了研究，但并未将里程焦虑作为补能诱导因素。

为了使驾驶员更好地响应诱导策略，提高对诱导方案的满意度，有必要建立诱导激励机制。例如，王卉等[12]在优化共享电动汽车调度时引入了价格激励手段，建立基于用户激励的共享电动汽车自适应调度成本最优模型。王宁等[13]构建了基于奖励机制的共享电动汽车双主体调配优化模型，在满足约束的前提下，根据相应的奖励措施，引导用户调整原出行方案，使之配合车辆调度员共同完成车辆调度。AUNG 等[14]通过引入激励手段提出了一种新的动态交通拥堵定价和电动汽车收费管理系统，该系统奖励选择不拥堵道路和不拥堵充电站的司机，并证明了该系统能够有效降低充电站的交通拥堵和总充电时间。由上述文献可知，激励机制研究使用的方法较多，但在电动汽车补能诱导激励上的研究较少。

在上述背景下，本文在充电站服务信息、道路交通信息及车辆补能信息三者交互的基础上，构建考虑负效应最小化的电动汽车补能诱导双层优化模型，其中，为了激励驾驶员响应补能诱导，建立了基于负效应调度贡献的激励机制。上层模型为路网补能负效应最小化的诱导激励模型；下层模型为带有补能站点选择的混行路网均衡模型。并利用算法求解双层模型，得出负效应最小化的补能车辆与站点的诱导方案。

1 问题描述

电动汽车补能是保障车辆在低续航时完成出行计划的必要条件，通常当电动汽车荷电状态低于某一阈值或无法完成剩余行程时产生补能需求，此时，驾驶员需前往充电站进行补能，然后再行驶至目的地。例如，某区域有2个充电站，其中，充电站1剩余4个充电桩，充电站2剩余1个充电桩，路网中同时存在多个补能车辆，即车辆1 和车辆2，t为路段的行驶时间，L为路段长度。驾驶员选择充电站具有利己性和随机性，在无补能车辆诱导的情况下，由于t2=10 min 小于t1=15 min，车辆1 将选择充电站2进行补能；与此同时，车辆2也将选择距离较近的充电站2进行补能。因此，造成了补能车辆在充电站2 处聚集，导致局部充电站负荷较高，加之电动汽车补能时间较长，充电站服务能力有限，在站内产生了排队现象，额外增加了驾驶员的行程时间。此外，车辆行驶至充电站的路程不在出行计划中，额外增加了驾驶员的行驶里程，并且随着续航里程的不断降低驾驶员易产生里程焦虑。为此，对路网中多个补能车辆进行诱导，最小化网络中因补能行为导致的一系列负效应。电动汽车补能示例如图1所示。

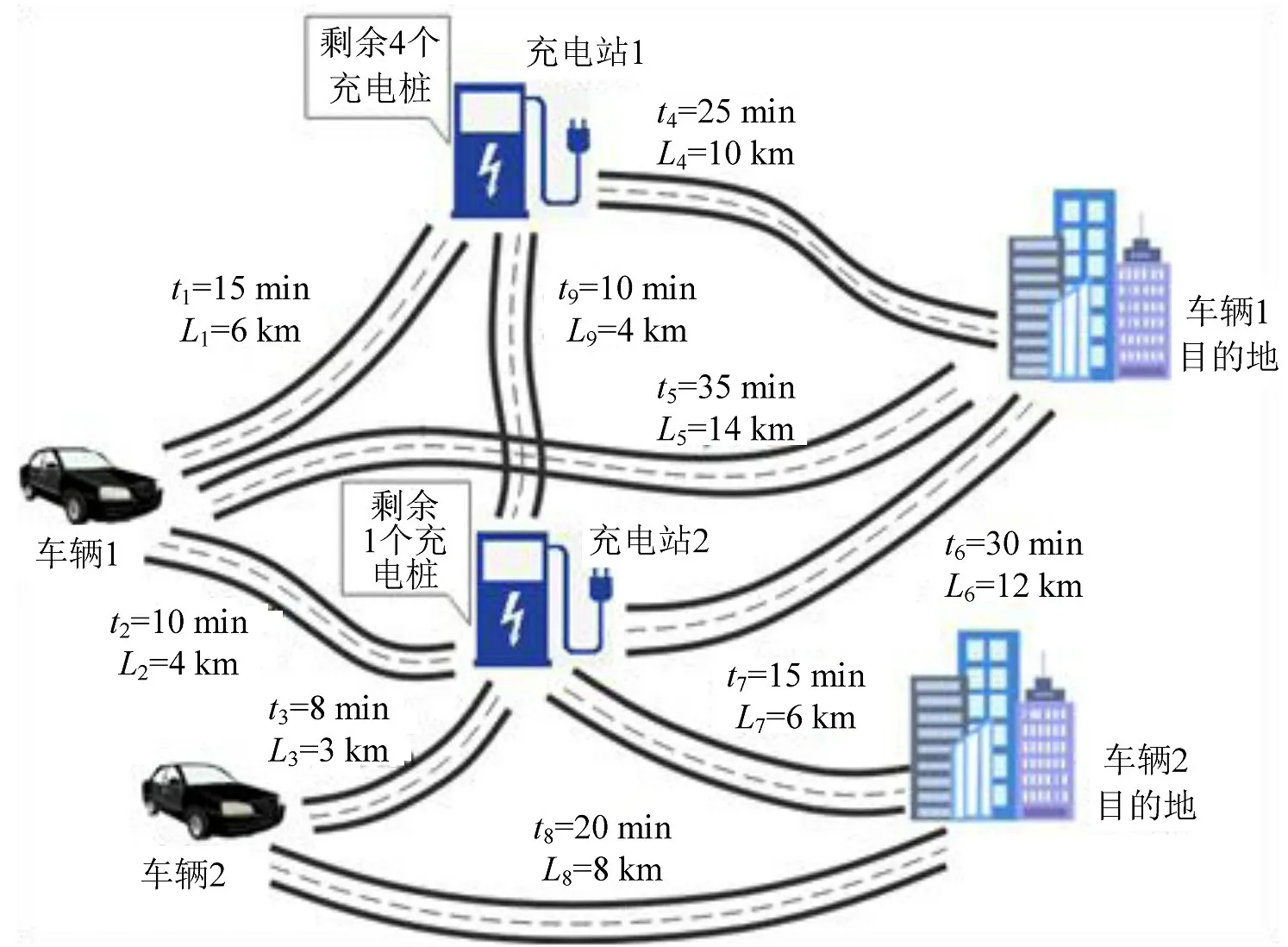
图1 电动汽车补能示例Fig.1 Example of electric vehicle charging

考虑交通路网G=(V,A)，其中，V为节点集，；A为路段集，，m为路段总数；路网上存在多组OD对，对OD对进行统一编号，N为OD 对总个数；gi为OD对i间的总出行需求；βi为OD对i间补能电动汽车渗透率；充电站皆位于路网节点上，对充电站进行统一编号，其中，r为充电站数目。补能车辆以产生补能需求的节点为起始点，根据站点与路段信息寻找补能站点，在站点补能后继续行驶至目的地。车辆在起点处的位置信息和剩余续航均已知。充电站位于道路节点上，充电站的位置信息和排队长度均可获知。

2 考虑负效应最小化的补能诱导双层优化模型

2.1 符号说明

本文符号及其物理含义如表1所示。

表1 符号说明Table 1 Symbol explanation

2.2 电动汽车补能

(1)电动汽车初始荷电状态度量

根据文献[15]中电动汽车荷电状态(SOC)与充电行为概率之间的统计关系可知，电动汽车的充电行为通常发生在其荷电状态低于60%时，同时，为了考虑初始荷电状态的渐变性，在此假设各OD对中电动汽车补能初始荷电状态服从三角分布，其概率密度函数为

式中：Bmin为补能车辆初始荷电状态的最低水平；Bmax为补能车辆初始荷电状态的最高水平；Bmod为补能车辆初始荷电状态的众数。本文中Bmin=0.2,Bmod=0.4,Bmax=0.6。

(2)电动汽车的电量消耗计量

OD对i间第n辆补能车辆到达充电站时的剩余电量与其从起始点O(i)到所推荐充电站j行驶的距离直接相关，计算式为

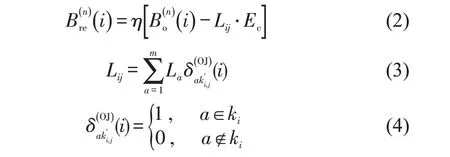
式中：η为能耗系数；Ec为电动汽车每公里耗电量；Lij为补能车辆由起始点O(i)到所推荐充电站j的距离。

(3)路段行程时间计量

交通路网中，车辆行驶速度受路段交通流量和道路通行能力约束，行驶速度的变化将影响电动汽车在道路上的行驶时间。因此，本文路段行驶时间采用美国联邦公共道路局(BPR)的路阻函数形式，即

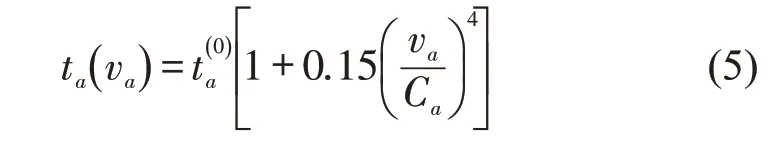
因此，补能车辆从O(i)到达所推荐充电站j的行驶时间为

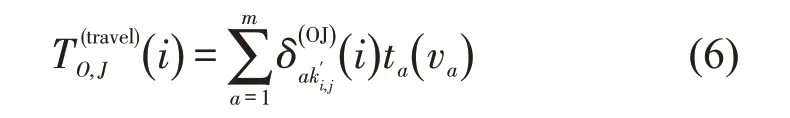
(4)充电站排队时间计量

电动汽车驾驶员除了考虑在道路上的行驶时间外，还需要考虑补能的排队等待时间。据观察，补能排队等待时间和出行时间随着交通流量的增加而增加。本文通过建立一个扩展的运输网络，将两种成本纳入一个统一的框架中[16]，如图2所示。

首先，加入伪弧线表示补能等待时间，如图2(b)中虚弧线所示。然后，将图2(a)中所示的弧{2}展开为图2(b)中{(2',2")}对弧。因此，经过充电站的路线，{1,3,2"}为充电路线，{1,2'}为非充电路线。

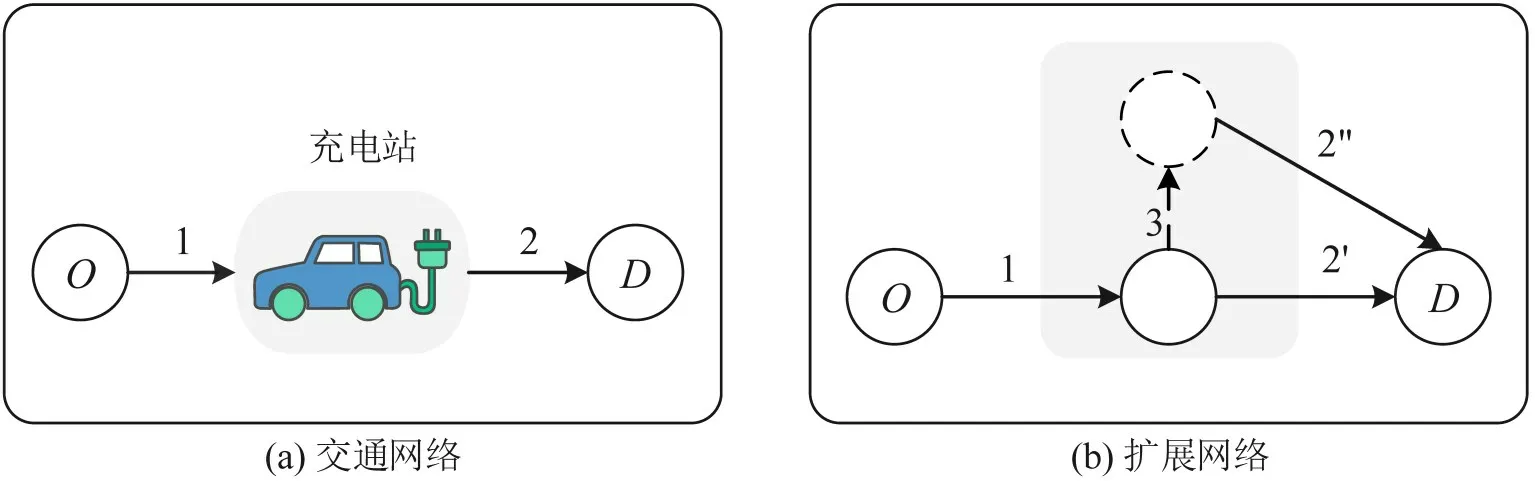
图2 交通网络和扩展网络Fig.2 Transport network and extended network

在M/M/1排队模型中，驾驶员在队列的平均等待时间为

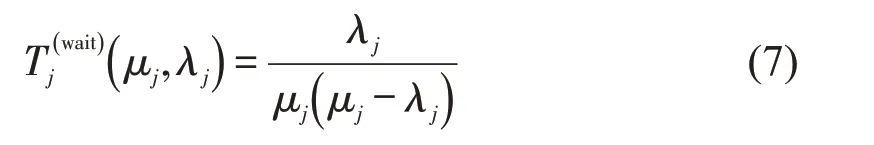
式中：λj为充电站j单位时间内的到达率；μj为充电站j的服务率(在M/M/1排队模型中，λj≤μj，以保证排队系统的稳定性)。对式(7)进行泰勒展开[7]为

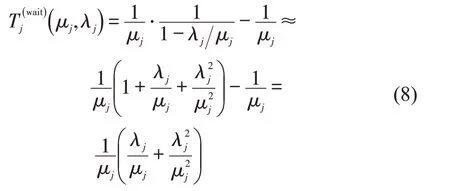
通过联合式(8)和BPR 函数的思想，可推导充电站的排队时间与补能流量的关系为

2.3 电动汽车补能负效应计量

电动汽车产生补能需求后，需前往充电站进行补能，再驶向目的地。因此，车辆的补能行为使驾驶员产生了额外的行驶里程和额外的行程时间，而且在前往充电站时，随着续航里程的降低，驾驶员会产生里程焦虑。并且在无补能车辆诱导的情况下，驾驶员选择充电站具有利己性和随机性，在补能高峰期时，易出现局部充电站车辆聚集的现象，不仅造成周围路段的交通拥堵，更增加了驾驶员的补能时间。因此，本文针对电动汽车补能带来的里程焦虑、额外行驶里程和额外行程时间建立补能诱导双层优化模型，最小化补能行为的负效应。

(1)里程焦虑成本计量

据调查，当电动汽车SOC超过20%～25%时，驾驶员会感觉到舒适[10]，然而，当SOC 低于这一舒适范围时，驾驶员就会担心电量耗尽。如果补能车辆还未到达充电站，但是，剩余电量下降到舒适点Bra以下，则随着电量的降低，驾驶员会变得越来越焦虑，从而产生心理成本；如果补能车辆到达充电站，其SOC 高于舒适点Bra则不产生里程焦虑成本。所以，补能车辆由O(i)到所推荐充电站j的平均里程焦虑成本为

式中：qij为OD 对i的补能车辆选择到充电站j的数量；cp为全国平均汽车牵引成本。

(2)额外行驶里程计量

考虑到补能车辆到其选择的充电站的方向应和前往目的地的方向保持一致，即不走“回头路”，因此，考虑补能车辆由起始点O到充电站J再到目的地D的行驶路程之和与该车辆没有触发补能需求时由起始点O至目的地D的行驶里程之差，此差值表示由补能行为产生的额外行驶里程，因此，补能车辆由O(i)到所选择的充电站j的额外行驶里程为

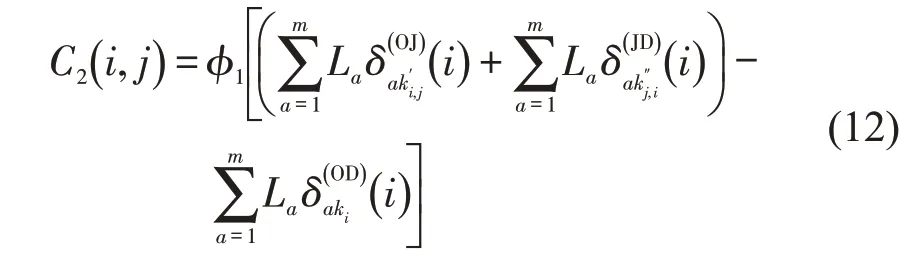
式中：φ1为将行驶里程转换为成本的系数。因为驾驶员需在电量耗尽之前到达充电站，所以，在额外行驶里程负效应中，对驾驶员影响最为关键的是由起始点O至充电站J的行驶距离。

(3)额外行程时间计量

当电动汽车触发补能需求后，完成行程所用时间包含电动汽车到达充电站的行驶时间，在充电站的等待时间，充电时间和从充电站到目的地的时间，所以，由补能行为带来的额外行程时间为触发补能需求后的行程总时间减去未触发补能需求的行程时间，即

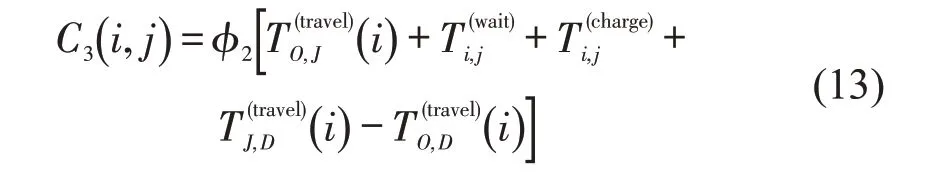
式中：φ2为将额外行驶里程转换为成本的系数。因为驾驶员选择充电站具有随机性，各个充电站的补能到达率各不相同，加之电动汽车补能时间较长，所以，充电站的排队等待时间具有较大差异。因此，在额外行程时间负效应中，对驾驶员影响最为重要的是充电站的排队时间。

2.4 补能诱导激励策略

当电动汽车前往充电站补能，需要较长的行驶路程或是较长的排队时间时，驾驶员在该充电站的补能意愿将会大大降低。因此，为了提高驾驶员对补能诱导的响应，根据电动汽车至充电站的行驶距离以及补能排队时间制定激励机制。首先，将驾驶员的行驶距离和补能排队时间分为低(L)、中(M)和高(H)这3 个等级；然后，将行驶距离等级与补能排队时间等级进行复合，将激励等级分为非常低(VL)、低(L)、中等(M)、较高(RH)、高(H)和非常高(EH)这6 个等级，每个等级取值分别为γij=1,2,3,4,5,6。

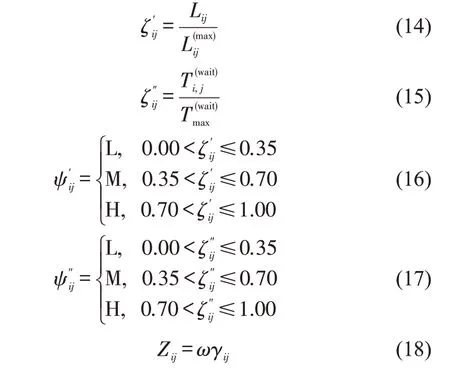
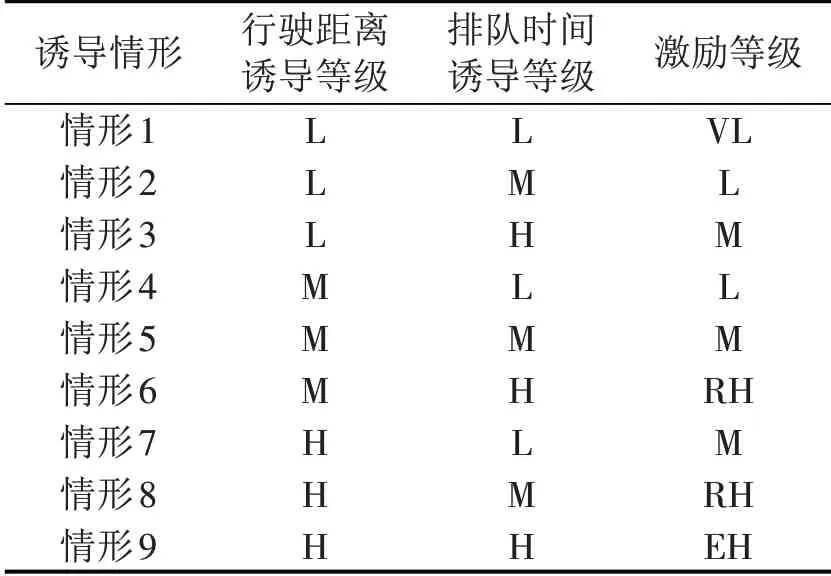
表2 补能诱导激励等级划分Table 2 Classification of charging induction excitation

情形1～3行驶距离诱导等级皆为低等级(L)，排队时间诱导等级逐级递增，因此，激励等级也由非常低(VL)递增为中等(M)；情形4～6 行驶距离诱导等级皆为中等级(M)，排队时间诱导等级依次递增，因此，激励等级由低(L)递增为较高(RH)；情形7～9行驶距离诱导等级皆为高等级(H)，排队时间诱导等级逐级递增，因此，激励等级也由非常低(M)递增为中等(EH)。诱导选择的充电站距离越远和排队等待时间越长，对驾驶员的补偿激励越多。

2.5 电动汽车补能诱导双层优化模型

由于充电站分布具有多样性，若仅以系统内所有补能车辆负效应最小为目标进行诱导并不适合，因此，本文还考虑了中间规划者的利益以及驾驶员补能负效应的均衡，建立补能车辆诱导双层优化模型，使模型的适用范围更加广泛。上层模型从中间规划者的角度出发，建立全局最优模型，使所有补能车辆的负效应最小和规划者给予驾驶员的补能激励最小。

上层模型目标函数为

约束条件为

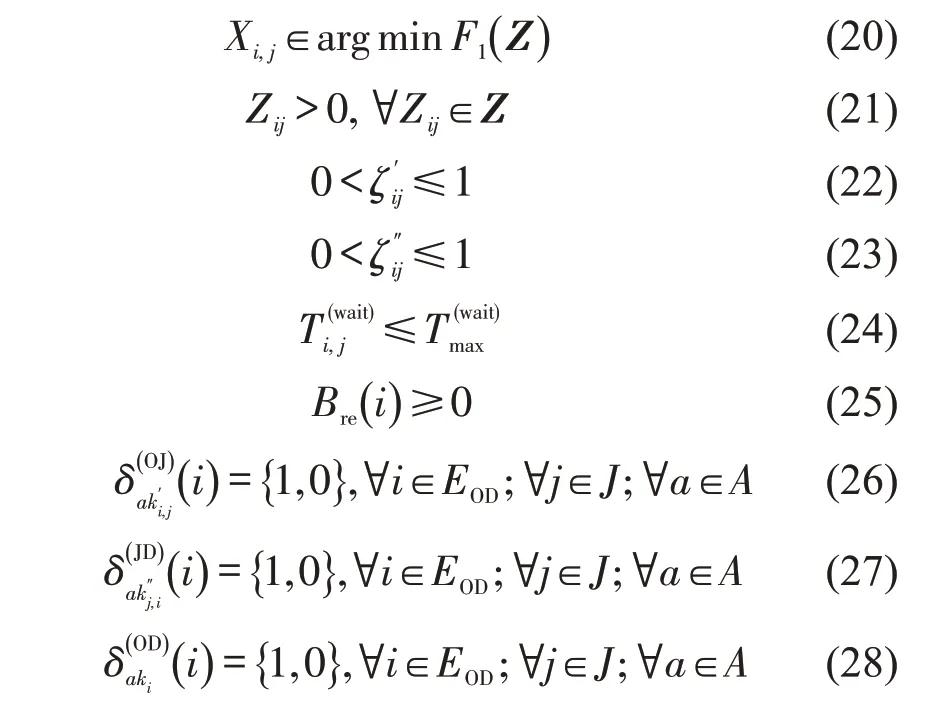
式(19)为上层模型的目标函数，其中，Z为该层模型的决策变量，即补能OD对的激励矩阵。约束条件：式(20)表示下层变量Xi,j是使上层模型最小化的解；式(21)为激励矩阵的约束；式(22)和式(23)为补能车辆的距离诱导贡献和排队等待时间诱导贡献的约束；式(24)为驾驶员的等待时间约束；式(25)为补能车辆i的剩余电量约束，使补能车辆到达充电站时其荷电状态大于等于零；式(26)～式(28)为0-1变量约束。

下层模型根据电动汽车补能负效应最小化的关键因素构建补能负效应用户均衡模型。在车辆进行补能时，对负效应影响最为关键的两个因素为由起始点O至充电站J的行驶距离和在充电站J的排队等待时间。首先，当电动汽车处于低续航状态时，驾驶员更关心的是在电量耗尽之前能否安全到达充电站，并且当SOC低于舒适点Bra时驾驶员还会产生里程焦虑成本，因为里程焦虑成本与补能车辆至充电站的行驶距离具有直接关系，所以，为了最小化驾驶员的补能负效应，将起始点O至充电站J的行驶距离作为影响负效应的关键因素之一。再者，因为各个充电站的充电桩数与补能车辆数不同，所以，充电站的排队等待时间也有所不同，甚至有可能相差较大。因此，将排队等待时间作为影响负效应的另一关键因素。除以上两个因素外，中间规划者对于驾驶员的补能诱导激励也是影响驾驶员选择充电站的重要因素。因此，下层模型从驾驶员补能负效应均衡的角度建立模型。

下层模型为

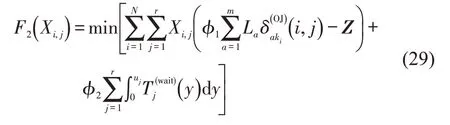
约束条件为

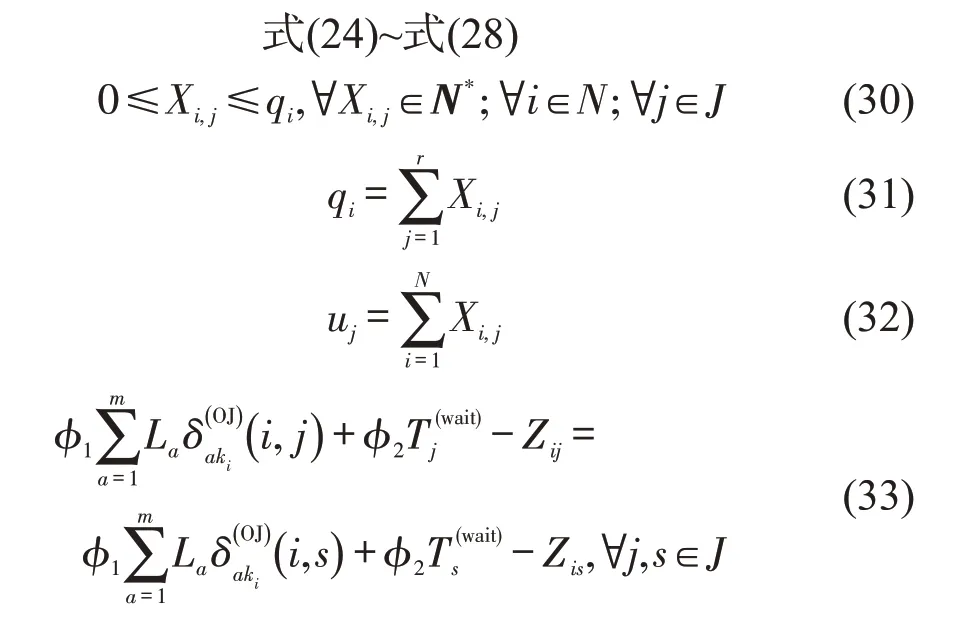
式(29)为下层模型的目标函数；式(30)为Xi,j的取值约束，其中N*为正整数集；式(31)为OD对i中的补能车辆流量守恒约束；式(32)为充电站j的补能流量约束，即充电站j的补能流量等于各补能OD对到充电站j的流量之和；约束条件式(33)表示同一OD对中补能车辆的负效应均衡。

3 设计求解算法

设计算法求解补能诱导双层优化模型。其中，上层模型是基于诱导激励的补能负效应最小化模型，遗传算法具有优秀的全局搜索能力，其收敛解与最优解的差异是可接受的，并且在求解基于用户激励的车辆引导或车辆调度问题时，遗传算法相较于贪心算法和模拟退火算法在收敛趋势和收敛速度上都具有较大优势[13,17]。因此，采用遗传算法求解上层模型，搜索负效应最小化的补能激励方案。下层模型是带有补能站点选择的用户均衡模型，Frank-Wolfe 算法是用于求解交通分配问题的经典算法，在每次迭代中，Frank-Wolfe 算法沿可行下降方向在可行域内进行一维搜索求解当次迭代的最优移动步长，得到下一个迭代点，重复迭代直至找到最优解，可以较好地保证解的质量[7,18]。因此，本文结合遗传算法和Frank-Wolfe算法求解提出的模型，该算法在理论上可以找到电动汽车最佳的补能激励方案，在算法实际运行中能够在有限时间内得到较优解。具体步骤如下：

Step 1 初始化。输入路径网络、OD 对出行需求、充电站站点、各弧段初始行驶时间、路段容量、相关参数取值及算法结束条件等数据。

Step 2 编码并生成初始种群。采用整数离散的方式对染色体进行编码，编码区间为[Smin,Smax]，对激励方案进行数字编码，通过编码形成初始种群，即补能车辆前往不同充电站的补能激励方案。

Step 3 将上层的补能诱导激励方案代入到下层模型中，并通过Frank-Wolfe算法对OD对中的补能车辆与非补能车辆进行配流，更新路径流量与路段行驶时间。判断是否满足收敛性标准，满足，则进入Step 4；不满足，则返回Step 2。

Step 4 计算适应度函数。将Step 3 得到的补能车辆分配方案返回到上层模型，计算适应度函数并进行评价，根据评价结果对染色体进行交叉和变异，产生新的种群。

Step 5 判断是否满足算法结束条件，若满足，则输出补能诱导方案；否则，返回Step 3。

4 算例分析

以Nguyen-Dupius网络为例验证所提出的模型和算法，这个小型网络由13 个节点、19 个路段和4个OD对组成，箭头处括号内数字分别代表路段长度(km)、自由流时间(min)、路段通行能力(pcu)。路网中设有3 个快速充电站，位于节点6、9 和11。假设6、9、11 充电站皆为同质充电站；模型中电动汽车型号一致，电池容量为54 kWh，途中补能车辆至多补能一次，模型参数在文献[5,7,10,19,20]研究基础上，取值如表3所示，每个OD对的出行总需求如表4所示。

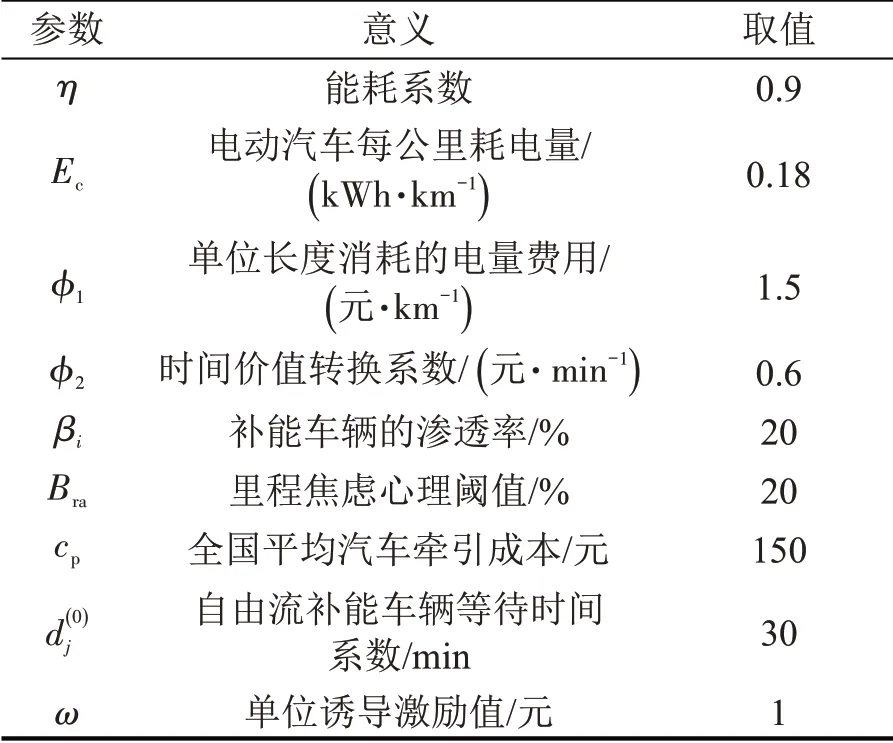
表3 模型参数取值Table 3 Model parameter value

表4 OD对出行需求Table 4 OD to travel demand

4.1 结果分析

利用本文所提出的算法求解算例，得到最优激励等级方案如表5所示。补能诱导前后电动汽车补能负效应成本对比如图4所示。

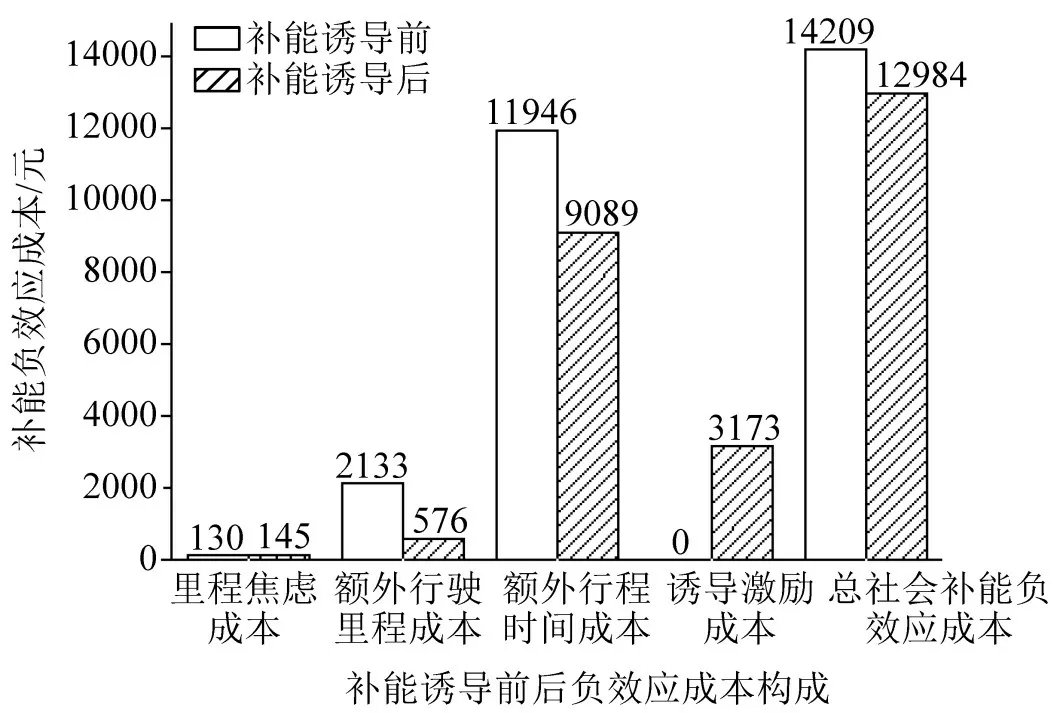
图4 补能诱导前后负效应对比Fig.4 Contrast diagram of negative effect before and after charging induction

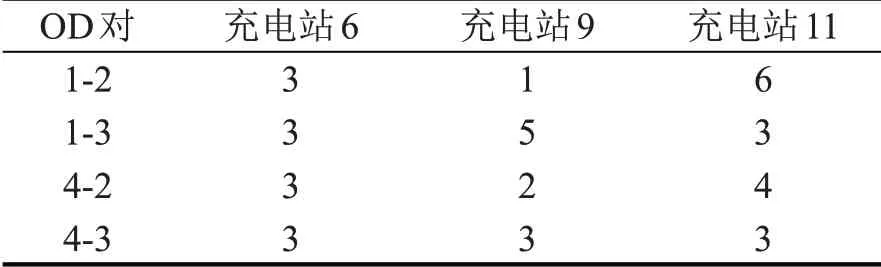
表5 最优激励等级方案Table 5 Optimal excitation level scheme

补能诱导后路网中所有电动车辆社会补能负效应总成本为12984 元，其中，驾驶员里程焦虑成本为146元，额外行驶里程成本为576元，额外行程时间成本为9089 元，规划者所支出的诱导激励成本为3173 元。对比无补能诱导激励时，所有车辆均采用距离最近的充电站进行补能。经计算，路网中总补能负效应为14209 元，其中，驾驶员里程焦虑成本为130 元，额外行驶里程成本为2133 元，额外行程时间成本为11946元。

通过分析算例结果可知，尽管本文所提出的补能诱导模型增加了规划者的激励成本，但是总社会补能负效应成本降低，证明了补能诱导的有效性。其中，在此算例中里程焦虑成本与额外行驶里程成本占比较小，因为Nguyen-Dupius路网相对较小，且充电站位置设置较为均衡。诱导前后补能车辆在各充电站的排队补能时间如表6所示。

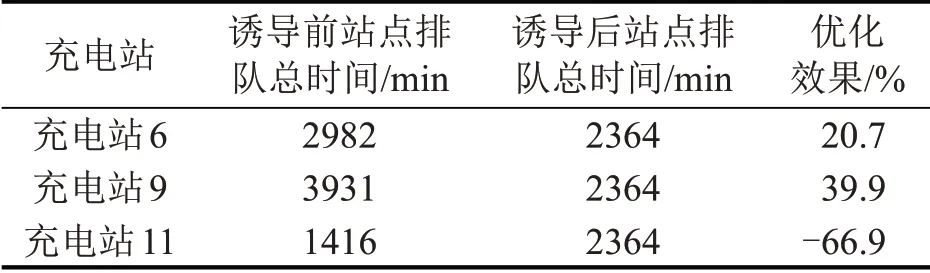
表6 诱导前后充电站排队时间对比Table 6 Comparison of charging station queuing time before and after induction

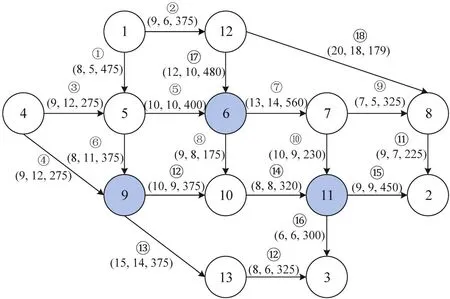
图3 Nguyen-Dupius路网Fig.3 Nguyen-Dupius road network

结果显示采用本文所提的补能诱导优化模型，驾驶员能够根据补能车辆的剩余电量情况、路网信息和充电站的排队时间选择合理的充电站，避免了诱导前补能车辆集中在充电站6或9进行补能的现象发生，使得区域内各个充电站的利用率更加均衡化，降低了由于集中补能对充电站的负效应，从整体上减少了驾驶员的补能排队时间。

4.2 灵敏度分析

(1)补能诱导激励单价灵敏度分析

为探讨不同的激励单价对补能负效应的影响，对补能诱导激励单价进行灵敏度分析，结果如表7所示。

表7 激励单价灵敏度分析Table 7 Excitation unit price sensitivity analysis

当激励单价为0.5 时，规划者所给予的补能激励成本较少，补能车辆前往诱导充电站的意愿较低，补能负效应优化效果不明显；当激励单价为1.0时，规划者所给予的补能激励成本相对较多，补能车辆前往诱导的充电站的意愿相对较高，补能负效应优化效果较为明显；当激励单价为2.0时，规划者所给予的补能激励成本多，补能车辆前往诱导的充电站的意愿高，但是补能车辆的额外行程时间总成本增大，其中，在额外行程时间成本中主要影响因素是充电站的排队等待时间，主要原因是驾驶员为了获取更高的激励成本可能会选择排队等待时间较长的充电站。

由激励单价灵敏度分析可知，当补能诱导激励较低时，补能车辆前往诱导充电站的意愿较低，补能负效应优化效果较差；而当补能诱导激励较高时，补能车辆可能会为了获得较高的补偿成本，而选择排队时间较长的充电站，加剧了补能负效应。

(2)电动汽车渗透率灵敏度分析

为探讨不同电动汽车渗透率对本文提出的补能诱导的影响，在保持OD对内出行需求不变的情况下，对电动汽车渗透率进行灵敏度分析结果如表8所示。

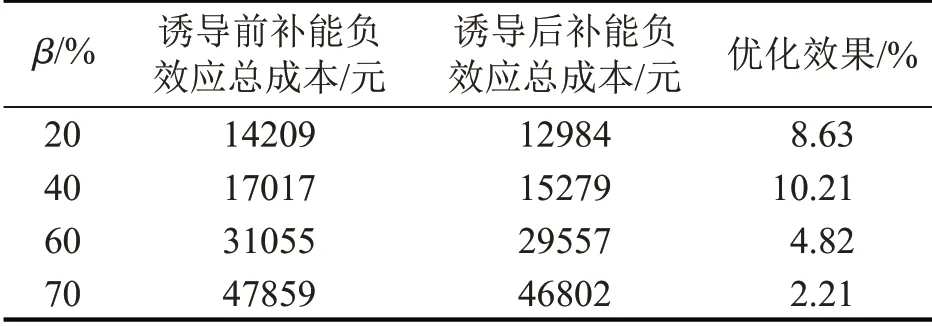
表8 电动汽车渗透率灵敏度分析Table 8 Permeability sensitivity analysis of electric vehicles

当补能OD对中的电动汽车的渗透率由20%提高到40%时，补能诱导的优化效果由8.63%提升至10.21%，但是，当OD 对中的电动汽车的渗透率由40%提高到60%或70%时，优化效果却降低。原因是由于路网中电动汽车数量过多，补能需求激增，远超于路网中充电站的供应能力，此时已不再是补能需求时空上的不均衡，而是路网中的充电站设施数量不足，应考虑增设充电站。

由电动汽车渗透率灵敏度分析可知，在保持OD 对内出行需求不变的情况下，适当增加电动汽车的渗透率可以提高补能诱导的优化效果；但是，当电动汽车渗透率持续升高时，若不增加路网中充电站设施的数量，则会加剧路网中补能车辆的负效应。

5 结论

针对电动汽车补能带来的一系列负效应问题，尝试采用激励诱导的方式，设置多个激励等级，平衡路网中的补能需求与供给。通过遗传算法和Frank-Wolfe 算法求解双层补能诱导模型，并通过路网算例验证了模型和算法的有效性。

算例结果表明：

(1)尽管本文提出的补能诱导双层优化模型增加了规划者的诱导激励成本，但是，所有补能车辆的总社会补能负效应成本降低，证明了补能诱导的有效性。

(2)随着激励效果的提升，规划者对补能车辆的诱导激励成本增大，但是，补能车辆的负效应却先降低后升高，因此，选择合适的补能诱导激励单价可以有效地减少规划者的成本支出，并降低路网中由补能带来的负效应。

(3)随着补能OD对中电动汽车的渗透率增加，路网中的补能需求远超于站点服务能力，此时，诱导激励手段已不能发挥较好的作用，应考虑增加路网中的充电站数量。