压裂井产量递减典型曲线图版的建立及应用
苏 畅 赵 刚 鹿克峰 时 琼
(1. 中海石油(中国)有限公司上海分公司 上海 200335; 2. 里贾纳大学 里贾纳 S4S 0A2加拿大)
中国致密气在鄂尔多斯盆地、四川盆地、塔里木盆地储量巨大,年产气量已超过500亿方,将是未来接替常规气的中坚力量。水力压裂是致密油气开采增产增储的最有效措施,对压裂井生产动态的可靠分析将为成功开采致密油气奠定坚实基础,例如试井解释在压裂井动态分析中发挥极其重要作用[1-6]。由于压裂井通常面临动态监测资料少、压力恢复测试过程压力恢复慢导致测试耗时长耗费高等难题,近20年随着致密气在世界大规模开采与现场对致密气开采认识加深,无需关井无需测压依靠长期生产数据的产量递减分析也成为压裂井动态分析重要手段。
递减分析技术具有悠久历史且实用性强,Arps于20世纪40年代提出著名指数递减、双曲递减、调和递减3种油气井生产进入边界控制(或称拟稳态)流动后产量随时间递减形式[7],由于其形式简单且无需已知油气藏各参数,至今仍然是现场最常用的递减技术。Fetkovich在Arps基础上整合生产井非稳态阶段递减提出新的递减典型曲线,实现油气井生产全周期递减分析[8]。Fetkovich递减理论更为重要的意义在于将典型曲线图版分析从试井解释扩展至产量递减分析,并且对递减率赋予油藏意义,将递减率与生产井产能、控制储量、储层Kh等参数联系起来,除了预测储量还能评价储层参数。然而,无论是Arps还是Fetkovich递减,其应用基础都建立在恒定井底流压条件下,一定程度上限制了应用。为此,Blasingame提出了物质平衡时间概念[9],在进入边界控制流后用物质平衡时间替换真实时间,使得恒定产量生产下的流动方程在变产量变流压生产条件下依然适用,基于生产井日产量与井底流压动态数据则可计算井控储量与采气指数;Blasingame进一步基于物质平衡时间建立了新的产量递减典型曲线图版[10]。随着物质平衡时间的提出,Agarwal等提出类似递减典型曲线[11]。Agarwal、孙贺东、陈济宇等[11-13]对多种经典产量递减分析技术进行了系统总结与讨论。然而,Fetkovich[8]、Blasingame[10]、Agarwal[11]经典产量递减典型曲线图版都是建立在直井生产基础上,即在油气藏流动进入边界控制流前它们仅适用于严格的径向流,而对于生产中伴随复杂流态的压裂井,特别是具有复杂裂缝系统的分段压裂水平井,且致密储层非稳态流动阶段长,应用经典产量递减图版会对分析结果带来误差且无法评价裂缝延伸长度。
本次研究应用点源函数(或称格林函数,在温度扩散与油藏压力扩散研究领域应用广泛[1,14-21])求取压裂井全生产周期产量随时间递减的解析解,基于计算的压裂井产量解、储层岩石与流体参数、油气藏泄流面积、压裂级数、裂缝长度,建立特地针对压裂井的新的产量递减典型曲线图版。
1 压裂井非稳态产量解析模型建立
以多级分段压裂水平油井为研究对象(图1,其中压裂直井即是裂缝条数为1的一个特例),论述压裂井非稳态流动解析模拟方法,为简洁阐述解析方法的建立与考虑实际应用的简便性,对模型提出以下简化假定:

图1 多分段压裂水平井模型示意图及模型坐标系统Fig.1 Hydraulically multistage fractured horizontal well schematic and coordinate system
1) 油藏边界为规整矩形,储层物性均质且仅考虑单相流体流动;
2) 裂缝纵向贯穿储层厚度,形成油藏内二维平面流动;
3) 裂缝导流能力无限大,忽略裂缝宽度影响,沿裂缝长度无压降;
4) 沿水平井筒每一分段水力压裂产生仅一条裂缝且与水平井筒方向正交;
5) 忽略储层流体直接流入水平井筒,即井的流量全部由裂缝生产贡献,通过水平井筒导入井底;
6) 忽略沿水平井筒导流造成压降,水平井筒处处压力相等;
7) 忽略储层启动压力梯度、非线性流动等复杂渗流机理。
1.1 压裂井生产造成油藏内任一点压降方程式
基于点源函数结合纽曼乘积(Newman Product)原理[22],多分段压裂水平井在封闭油藏内任一点压降等于
Δp(x,y,t)=pi-p(x,y,t)=
psy(yk,y,t-τ)dx′
(1)

psx(x′,x,t-τ)=
(2)
其中
(3)
式(2)、(3)中:ηx为x方向扩散系数,m2/d;xe为油藏长度,m;Kx为x方向渗透率,mD;μ为流体黏度,mPa·s。

图2 压裂井数学模型中对裂缝长度的离散Fig.2 Discretization of fracture in mathematic model
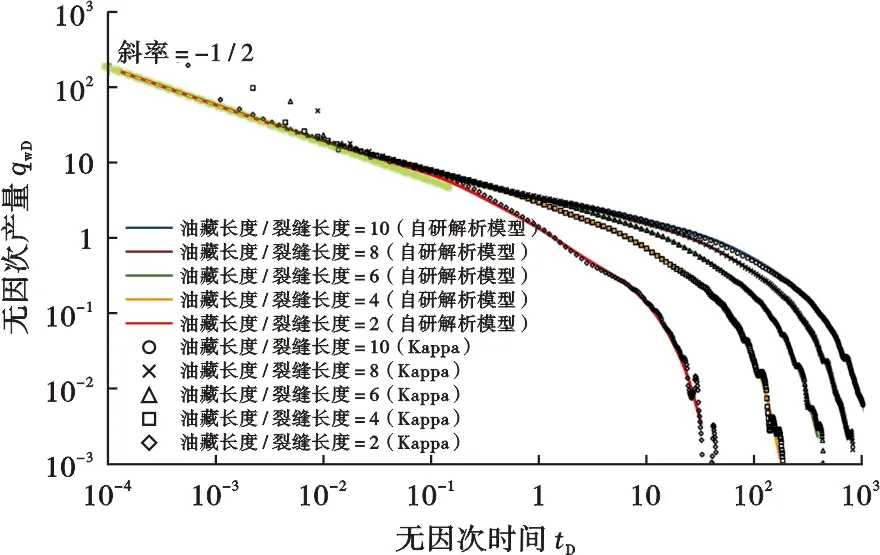
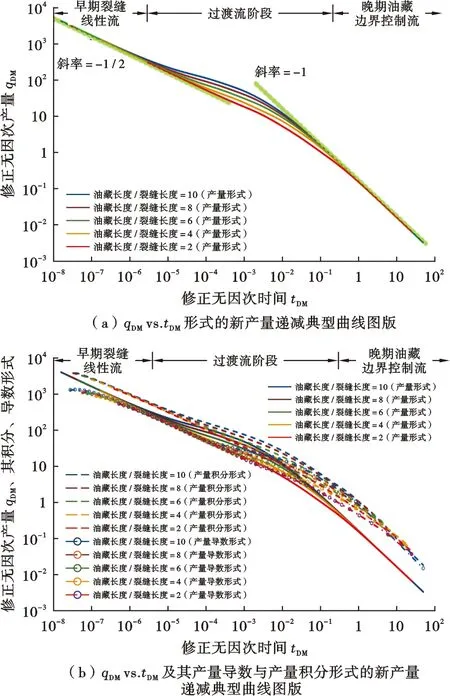
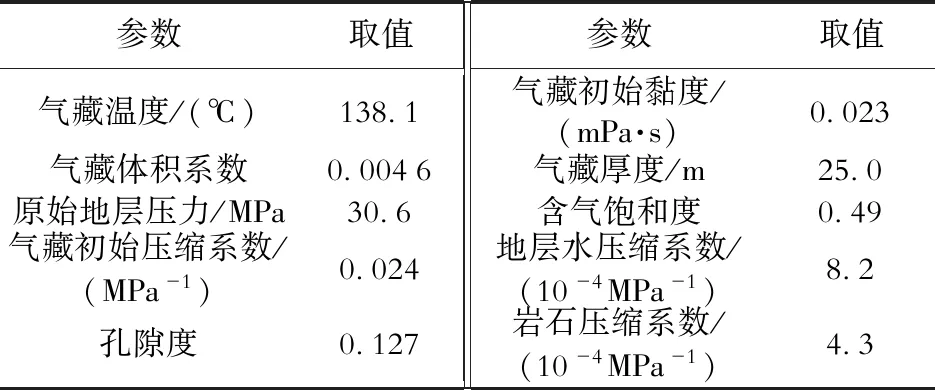
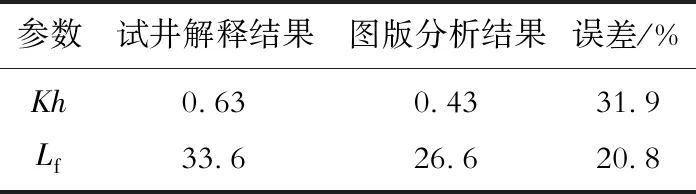
xf1=x0 xj+1<… 假设流体通量沿每一裂缝离散段为常数(只随时间变化),第k条裂缝的第j离散段流体通量则近似等于 (xj-1 (4) 式(4)中:Lf为裂缝半长,m;q为流量,m3/d。 结合式(4),式(1)可进一步表述为 (5) 对裂缝第j离散段点源函数x方向积分展开可得 (6) 将式(6)、式(2)代入式(5),多分段压裂水平井非稳态压降最终表述为 (7) 式(7)可简洁表述为 Ipsx(xj-1,xj,x,t-τ)·psy(yk,y,t-τ)dτ (8) 本次研究油藏非稳态压力与流量首先将在拉普拉斯域中求解,定义拉普拉斯算子 (9) 式(9)中:u为拉普拉斯变量。 基于拉普拉斯变化卷积定理,对式(8)等式左右两边做关于时间的拉普拉斯变化 L[Ipsx(xj-1,xj,x,t)·psy(yk,y,t)] (10) 针对式(10)等式右边x,y方向源函数的乘积没有拉普拉斯解析变换式的难题,采用Zhao和Thompson建立的计算速度快且精度高的数值拉普拉斯变换方法[17],则复杂的拉普拉斯变换L[Ipsx(xj-1,xj,x,t)·psy(yk,y,t)]可通过数值积分计算。 图1所示多分段压裂水平井模型将通过假定的裂缝具有无限导流条件进行系统耦合,即沿裂缝压力处处相等。在拉普拉斯域,首先基于式(10)评价裂缝每一离散段中点压降,并将每条裂缝相邻离散段中点压力创建等式,则可建立Nstage·(m-1)个线性方程组;再有基于假定6(沿水平井筒无压降)将裂缝与水平井筒相交的裂缝离散段中点压力创建等式,则可建立(Nstage-1)个线性方程组;最后,根据相应的内边界条件(油井生产条件),建立最后一个(第Nstage·m个)线性方程。油井以恒定井底流压生产,则有 L[Ipsx(xj-1,xj,xw+rw,t)·psy(yk,yk,t)] (11) 式(11)中:pwf为井底流压,MPa。 至此,总共建立(Nstage·m)个线性方程组,同时方程组具有同等数量的未知数,求解线性方程组,则可获取拉普拉斯域中所有裂缝离散段对应的流量,所有离散段流量之和等于压裂井产量。 将拉普拉斯域中求取的裂缝离散段流量代入式(10),则可计算拉普拉斯域中油藏内任一点的压降,再通过Stehfest拉普拉斯数值逆变换方法[23],将前述获取的油藏压降与裂缝流量结果转换到真实时间域。 设定压裂井与油藏模型基础参数(表1),应用前述点源函数方法解析模拟压裂井全周期产量动态,以不同油藏长度(xe)与裂缝长度比值为例绘制典型曲线图版。 表1 压裂井与油藏模型基础参数Table 1 Basic parameters of fractured well and reservoir model 首先,传统压裂井无因次产量qwD与无因次时间tD定义如下: (12) (13) 式(12)中:qw为压裂井产量,m3/d;K为储层渗透率,mD。 按照表1设定参数作为模型的输入,产生的递减典型曲线qwDvs.tD结果如图3所示,初期所有曲线聚拢在一起以1/2斜率递减,反应初期裂缝引起地层线性流,线性流之后曲线各自分开,进入过渡流与边界控制流。 图3 多分段压裂水平井恒定井底流压条件下产量递减结果Fig.3 Production rate decline behaviors of multistage fractured horizontal well qwD vs.tD under constant bottom hole flowing pressure 为验证解析模拟结果的正确性,与商业软件Kappa模拟结果进行了对比(图3),两者一致性好;但Kappa计算的早期与晚期结果不稳定、精度欠缺,而本文计算的结果稳定、曲线光滑、精度高,为建立新的典型曲线图版奠定坚实基础。图3所示曲线形态特征不典型,在实例分析应用中不易实现与真实压裂井产量的准确拟合。 为创造更具特征、更方便现场应用、兼顾压裂井生产全周期的递减典型曲线图版,创新性定义同时整合储层岩石与流体参数、泄流面积、裂缝长度、裂缝条数的修正无因次产量qDM、修正无因次时间tDM、对比裂缝长度与油藏面积的“Scaler”。将图3中曲线以qDMvs.tDM形式重新绘制,实现新产量递减典型曲线图版的建立(图4)。 修正无因次产量与修正无因次时间定义为 (14) (15) 无因次物质平衡时间tmbD[9]定义为 (16) “Scaler”定义为 (17) 如图4a所示,新建立的典型曲线图版整体以非常独特的、有规律的形式呈现,所有曲线在早期与晚期聚拢在一起形成两个“曲线簇”,在中间过渡区域分开,早期以1/2斜率递减反映裂缝引起地层线性流、晚期以单位斜率递减反应边界控制流、早晚期流态中间为过渡阶段系统性响应油藏与压裂井相对几何关系(各流态如图5所示)。同时,图4b呈现包括图4a所示产量形式典型曲线外还呈现产量积分与产量导数形式典型曲线。应用类似的方法与步骤,可以自行建立各种不同油藏长、宽、裂缝长度、裂缝数量、裂缝间距等条件下的qDMvs.tDM递减典型曲线图版。 图4 新的产量递减典型曲线图版Fig.4 Newly established production decline type curves 图5 多分段压裂水平井随生产流态变化示意图Fig.5 Flow regimes illustration of multistage fractured horizontal well 选取鄂尔多斯盆地某致密气田在生产一口多分段压裂水平井、东海盆地在生产一口压裂直井为研究对象,详细阐述新建立图版在实例分析中的具体应用步骤及结果。为清晰呈现新递减图版与实际生产数据的拟合,本次实例应用的图版典型曲线只包括产量形式。另外,针对气体PVT性质随开采过程变化,应用规整化拟压力替代压力,气藏规整化拟压力定义为 (18) 式(18)中:下标“i”表示气藏初始状态;z为气体z因子,无量纲;pb为一个大气压,MPa。 X气井至今生产750天(图6),沿水平井筒实施5段水力压裂,相邻分段中点距离分别为100、200、200、100 m,表2汇总了气藏基础参数。 图6 X井天然气产量与井底流压动态Fig.6 Production rate and bottom hole flowing pressure of Well X 表2 X井与气藏基础参数Table 2 Basic parameters of Well X and the gas reservoir 3.1.1应用新建立图版分析X井 应用新建立的图版分析X井主要包括4个步骤: 1) 基于地质描述,简化气藏边界形态为矩形并提炼长宽比(此例xe/ye=1/3),结合简化的气藏模型与水平井压裂分段相对位置应用前述方法,建立不同气藏长度与裂缝长度比值的高级产量递减典型曲线图版; 图7 新的产量递减图版与X井生产动态拟合Fig.7 New type curves matching with production dynamics of Well X 4) 计算关键参数,基于qDM定义(式14)与qwD定义(式12),计算气藏Kh 基于tDM定义(式15)与tD定义(式13),计算裂缝半长 其中,气藏综合压缩系数等于 cti=sgcg+swccwc+c=0.805×0.089+ 0.195×0.000 88+0.000 43=0.072 2 MPa-1 则裂缝半长等于 基于“Scaler”定义(式17),计算气井泄气面积为 21.42×5=269 280.4 m2 气井控制储量则等于 3.1.2商业软件提供图版分析X井 应用Kappa提供的经典Blasingame递减图版对X井进行实例分析,生产数据与图版整体拟合较差,Blasingame图版尤其不能很好地反映多分段压裂水平井复杂的过渡阶段流动(图8a);以后期拟合为首要目标,确保储量评价准确,最终分析结果显示控制储量3 890万方、Kh=45 mD·m,则K=4.5 mD,裂缝长度不能评价。另外,渗透率分析结果明显有误,X井所在区域取心空气渗透率约1 mD,气相有效渗透率不可能高达4.5 mD。同时应用经典Fetkovich图版对X井进行实例分析,整体拟合效果较Blasingame图版更差(图8b),最终分析结果显示控制储量5 000万方、Kh=16.6 mD·m,则K=1.66 mD。 图8 传统商业软件对X井的分析情况Fig.8 Production analysis of Well X with conventional decline type curves provided by commercial software Z井至今生产1190天,压裂返排后生产200天时进行过一次关井压力恢复测试。Z井生产动态如图9所示,表3汇总了Z井主要参数。图10为压力恢复试井压差与压力导数双对数诊断图,可以看出压力导数清晰呈现代表裂缝线性流动的1/2斜率特征线,通过试井分析获取地层系数Kh=0.63 mD·m、裂缝半长Lf=33.6 m。 图9 Z井天然气产量与井底流压动态Fig.9 Production rate and bottom hole flowing pressure of Well Z 表3 Z井与气藏基本参数Table 3 Basic parameters of Well Z and the gas reservoir 图10 Z井压力恢复试井双对数诊断图分析Fig.10 Pressure buildup Log-Log diagnostic plot of Well Z 结合地质描述,针对Z井,解析模型中ye/xe=3/4,裂缝条数Nstage=1,计算产量解析解,并建立典型曲线图版qDMvs.tDM。如图11所示,Z井动态与压裂直井典型曲线xe/(2Lf)=8实现最佳拟合,对应Scaler=192。具体分析步骤与上述实例类似,气藏Kh计算有 图11 新的产量递减图版与Z井生产动态拟合Fig.11 New type curves matching with production dynamics of Well Z 裂缝半长计算有 气井泄气面积计算有 192×26.62×1=135 851.5 m2 气井控制储量则等于 表4汇总了不同方法获取的地层Kh与Z井裂缝半长,以试井解释结果为基准,新建立递减图版分析针对该2个参数产生误差分别为31.9%与20.8%,整体一致性较好,可作为对结果相互验证相互参考的依据。 表4 不同方法评价地层系数与裂缝半长结果对比Table 4 Comparison of reservoir flowing capacity and fracture half length results by different methods 1) 新建立的产量递减典型曲线特地针对压裂井提出,考虑压裂井生产引起的复杂流态,通过与实际压裂井的生产数据拟合实现储层Kh、裂缝长度、气(油)井泄气(油)面积、井控储量等关键信息的获取,为致密储层压后动态分析提供重要价值。 2) 新建立的产量递减典型曲线以独特、富含规律的形式呈现,所有曲线在早期线性流与后期边界控制流均重合在一起,中间过渡流部分反应压裂井与储层渗流边界相对几何关系,典型曲线对压裂井流态变化的诊断功能促进与实际压裂井生产数据的拟合,增进对压裂井与储层的系统性认识。

1.2 拉普拉斯变换

1.3 系统耦合及压裂井产量解获取
2 新的压裂井产量递减典型曲线图版建立


3 实例应用
3.1 实例1——多分段压裂水平井X



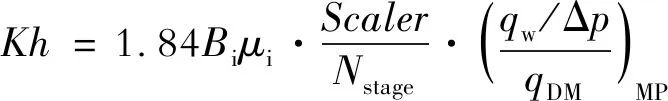

3.2 实例2——压裂直井Z



4 结论

