Sine Trigonometry Operational Laws for Complex Neutrosophic Sets and Their Aggregation Operators in Material Selection

D.Ajay,J.Aldring,G.Rajchakit,P.Hammachukiattikul and N.Boonsatit

1Sacred Heart College(Autonomous),Tamil Nadu,635601,India

2Maejo University,Chiang Mai,50290,Thailand

3Phuket Rajabhat University,Phuket,83000,Thailand

4Rajamangala University of Technology Suvarnabhumi,Nonthaburi,11000,Thailand

ABSTRACT In this paper,sine trigonometry operational laws(ST-OLs)have been extended to neutrosophic sets(NSs)and the operations and functionality of these laws are studied.Then,extending these ST-OLs to complex neutrosophic sets(CNSs)forms the core of this work.Some of the mathematical properties are proved based on ST-OLs.Fundamental operations and the distance measures between complex neutrosophic numbers(CNNs)based on the ST-OLs are discussed with numerical illustrations.Further the arithmetic and geometric aggregation operators are established and their properties are verified with numerical data.The general properties of the developed sine trigonometry weighted averaging/geometric aggregation operators for CNNs(ST-WAAO-CNN&ST-WGAO-CNN)are proved.A decision making technique based on these operators has been developed with the help of unsupervised criteria weighting approach called Entropy-ST-OLs-CNDM (complex neutrosophic decision making)method.A case study for material selection has been chosen to demonstrate the ST-OLs of CNDM method.To check the validity of the proposed method,entropy based complex neutrosophic CODAS approach with ST-OLs has been executed numerically and a comparative analysis with the discussion of their outcomes has been conducted.The proposed approach proves to be salient and effective for decision making with complex information.

KEYWORDS Complex neutrosophic sets (CNSs); sine trigonometric operational laws (ST-OLs); aggregation operator;entropy; CODAS; material selection; decision making

1 Introduction

One of the complex problems in all types of industries/companies is making decisions based on ambiguous information.As a consequence,the concept of fuzzy set theory has been employed to deal with this type of situation or problem.Zadeh [1] first proposed the concept of fuzzy subsets in 1965.It has sparked numerous significant outcomes in the scientific community,which have been replicated in modern applications,particularly in decision-making and artificial intelligence.In addition,different researchers have extended the core idea of fuzzy sets to handle different types of uncertainty,and the extended notions of fuzzy sets include intuitionistic fuzzy sets (IFSs)[2],Pythagorean fuzzy sets (PFSs)[3],Fermatean fuzzy sets (FFSs)[4],Neutrosophic sets (NSs)[5],and Spherical fuzzy sets (SFSs)[6] among others and each of them addresses the problem of uncertainty in a unique way.Based on these notions,various multi criteria decision making (MCDM)approaches are available in the literature like weighted sum method(WSM),weighted product method (WPM),the multiple criteria optimization compromise solution(VIKOR),the technique for order performance by similarity to the ideal solution (TOPSIS),the Weighted Aggregates Sum Product Assessment (WASPAS),COmbinative Distance-Based ASsessment (CODAS),and the Evaluation Based on Distance from Average Solution (EDAS),etc.,MCDM is a technique for selecting the best option from a set of alternatives and neutrosophic sets have found wide scope in such techniques.Edalatpanah established a new model of data envelopment analysis based on triangular neutrosophic numbers [7].And also neutrosophic approach have been implemented to data envelopment analysis with undesirable outputs by Mao et al.[8].A new ranking function of triangular neutrosophic number [9] and systems of neutrosophic linear equations are introduced by Edalatpanah [10].

Complex fuzzy sets (CFSs)are a significant research area of investigation in fuzzy logic.It was proposed by Ramot et al.[11,12].CFSs use a complex membership function to handle uncertainty with periodicity which takes complex values within the complex unit circle.Clearly,the complex memership functionM=μeiαof a CFS comprises two terms named amplitude termμand phase termαwhich lie in the intervals [0,1] and [0,2π],respectively.The phase term accounts for the periodicity of the data and distinguishes CFSs from the traditional models of fuzzy set theory.CFSs and Complex Fuzzy Logic (CFL)have been utilized to develop accurate and efficient time series forecasting models [13,14],image processing [15],etc.The concept of CFSs,has been further extended to complex intuitionistic fuzzy sets (CIFSs)[16],complex Pythagorean fuzzy sets(CPFSs)[17],complex neutrosophic sets (CNSs)[18] and so on and also it is evident from the literature that notable research have been carried out in complex fuzzy sets scenario.Recently,Xu et al.[19] introduced an extended EDAS method with a single-valued complex neutrosophic set and its application in green supplier selection.Complex neutrosophic generalized dice similarity measures have been developed by Ali et al.[20].Also,another MCDM model called a soft set based VIKOR is developed based on CNSs by Manna et al.[21].Some of complex hybrid weighted averaging operators are introduced for decision making in [22].Aggregating the fuzzy information plays an important role in decision theory and it is involved in majority of MCDM methods.

In addition operational laws also play a vital role in aggregation process.Also it is evident from the literature that various operational laws are available.Gou et al.[23] used new type of operational laws for IFSs.Then,Li et al.[24] introduced the logarithmic operational laws for IFSs in order to aggregate information.Later,Garg et al.[25] introduced a new logarithmic operational laws for single valued neutrosophic number which yields application in multi attribute decision making.Also,Ashraf et al.[26] used logarithmic hybrid aggregation operators for single valued neutrosophic sets.In continuation,Garg et al.[27] have presented some new exponential,logarithmic,and compensative exponential of logarithmic operational laws for complex intuitionistic fuzzy (CIF)numbers based on t-norm and co-norm.Garg also utilized the logarithmic operational laws for PFSs in [28].Further,Nguyen et al.[29] developed exponential similarity measures for Pythagorean fuzzy sets and their application in pattern recognition.Haque et al.[30] utilized exponential operational laws for generalized SFSs.Another novel concept of neutrality operational laws have been introduced by Garg et al.[31] for q-rung orthopair fuzzy sets and Pythagorean fuzzy geometric aggregation operators [32].Also,Garg extended the new exponential operation laws for q-rung orthopair fuzzy sets in [33].

Sine trigonometric operational laws were introduced by Garg [34].The main advantage of sine trigonometric function is that it accounts for the periodicity and it is symmetric about the origin.Thus it satisfies the expectations of the decision-maker over the multi-time phase parameters.Garg [35] introduced a novel trigonometric operation based q-rung ortho pair fuzzy aggregation operators and he also extended these operational laws to Pythagorean fuzzy information [36].Abdullah et al.[37] developed an approach of ST-OLs for picture fuzzy sets.Ashraf et al.[38]utilized the concept of single valued neutrosophic sine trigonometric aggregation operators for hydrogen power plant selection and further they implemented these operational laws for spherical fuzzy environment in [39].MCDM methods namely TOPSIS and VIKOR have been developed based on ST-OLs by Qiyas et al.[40,41].From the literature,it is clear that ST-OLs play predominant role in aggregation operators (AOs).Through this motivation and considering the advantage of ST-OLs,some new ST-OLs for CNSs must be established and their behaviour in complex scenario needs to be studied.Hence,this paper aims to modify sine trigonometric operational laws for complex neutrosophic sets and implement them in complex decision making method for material selection.So,the main objective of this paper can be described as follows:

(i).To present the ST-OLs for CNSs

(ii).To obtain some of the distance measure for complex neutrosophic sets based on ST-OLs

(iii).To develop an MCDM technique with the help of the proposed aggregation operators

(iv).To demonstrate an entropy technique based on ST-OLs for CNNs in order to attain complex weights of criteria

(v).To give an application of the proposed MCDM method in material selection in an industry

(vi).Finally,to present the validation of the developed method with existing CODAS approach

The organization of the paper is the following; We review the basic concept of NSs in the second section of the paper.In Section 3,we explore the operations of enhanced ST-OLs for NSs.These ST-OLs have been extended to CNSs in Section 4,including subtraction and distance measurement of ST-OLs for CNSs.In Section 5,we develop AOs and prove their properties for ST-OLs of CNSs.In Section 6,an MCDM approach has been explained in detailed steps with entropy technique for criteria weights.The proposed MCDM approach is used to provide an application for material selection in Section 7.The validation and discussion of the study is carried out in Section 8.Finally,the paper is concluded in Section 9 with direction for further research.

2 Preliminaries

Some of the basic concepts of neutrosophic sets (NSs)with their operations are discussed here.

Definition 2.1[1] A fuzzy setdefined on a universe of discoursehas the form:

Definition 2.2[2] An intuitionistic fuzzy setis defined as a set of ordered pairs over a universal setand is given by

where:→[0,1],→[0,1] with the conditionfor each element∈.Here the membership and non-membership functions are denoted asand,respectively.

Definition 2.3[5] Letbe a universe of discourse or a non empty set.Any object in the neutrosophic sethas the formwhere,andrepresent the degree of truth membership,the degree of indeterminacy and the degree of false membership respectively of each element∈to the setand it is defined as

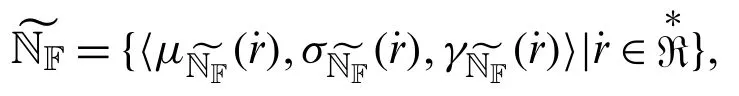
Definition 2.4[5] Letandbe three neutrosophic numbers (NNs)and let ¨wbe any scalar.

Then

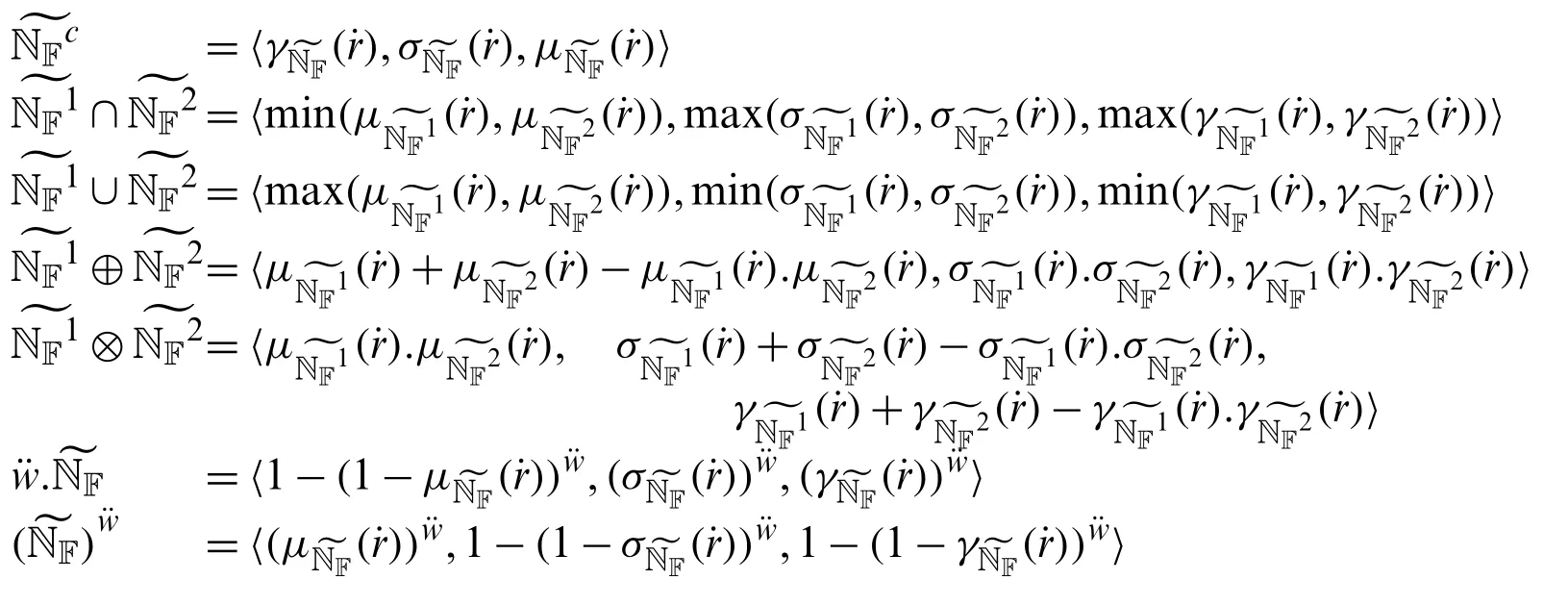
Definition 2.5Letbe two NNs.Then

Definition 2.6Letandbe three NNs.Then the score and accuracy functions of NNs are defined as follows:

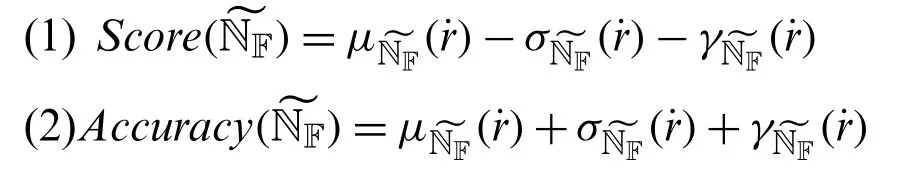
Also,the following conditions hold good.

3 Sine Trigonometry Operational Law(STOL)for Neutrosophic Sets

First,the STOL [34] are applied to neutrosophic sets and the boundary conditions are verified.

Definition 3.1Let the neutrosophic numbers (NNs)beThen,the sine trigonometric operational laws of NNs are defined as follows:

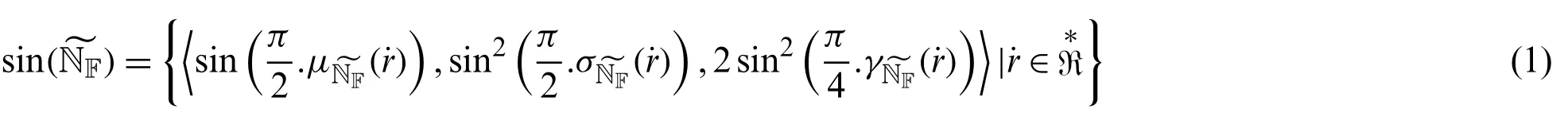
From the above STOL of NNs,it is evident that the sin()is also NNs.And it satisfies the following condition of neutrosophic set as the degree of truth,indeterminacy,and falsity of NS are defined,respectively

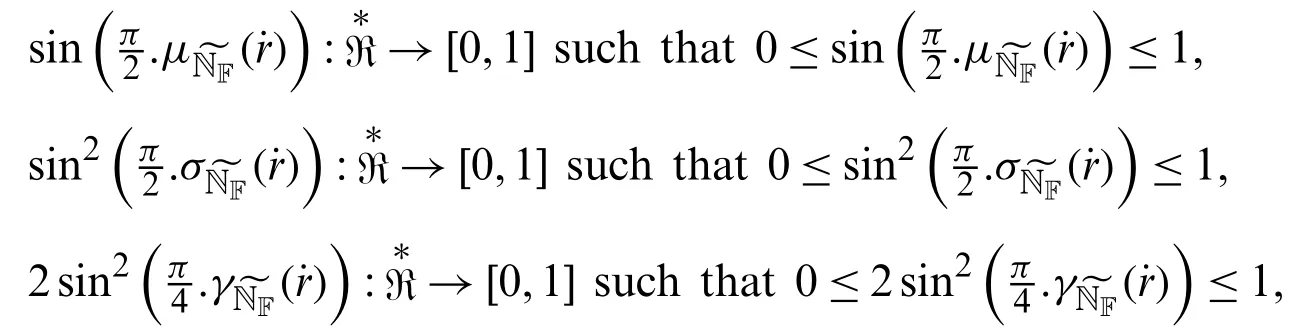
Then we discuss the fundamental operations on sine trigonometric neutrosophic numbers(STNNs)and their properties.

Figure 1:This is a graph of STOLs of NNs

Definition 3.2Letbe neutrosophic numbers (NNs)and let ¨wbe any scalar.Then

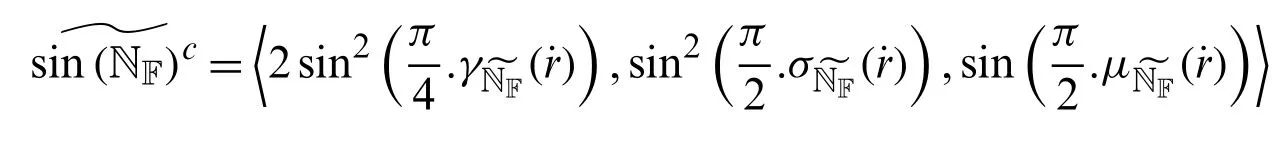
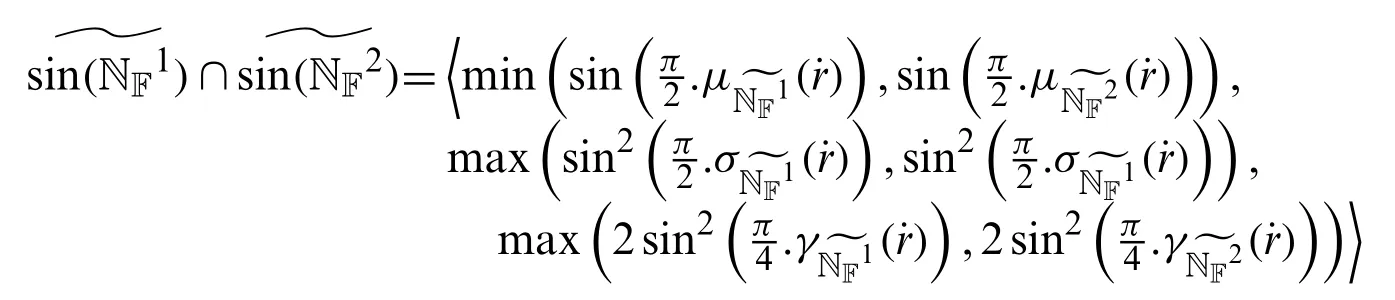
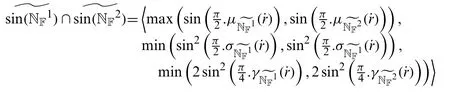
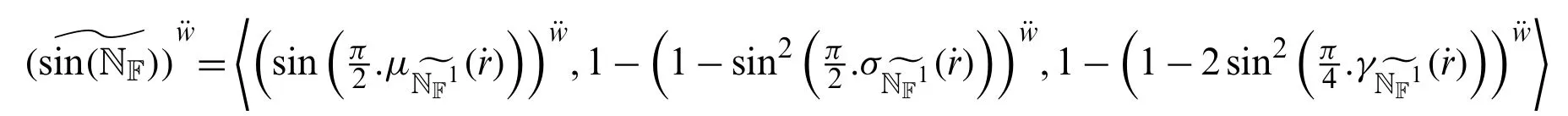
Definition 3.3Letbe two sine trigonometric neutrosophic numbers.Then

Definition 3.4Letbe a neutrosophic number.Then the score and accuracy functions of STOL of NNs are defined as follows:

Here the score and accuracy range values of STOLs of NNs are discussed in pictorial representation in the following Figs.2 and 3 when the membership values ofare equal.

Figure 2:This is a graph of score range values of STOLs of NNs

Figure 3:This is a graph of accuracy range values of STOLs of NNs

4 Sine Trigonometry Operational Laws(STOLs)for Complex Neutrosophic Sets(CNSs)

First,we see some basic concepts of complex neutrosophic sets and their operations.

Definition 4.1[18] A complex neutrosophic set,is represented by truth membership functionan indererminacy membership functionand a falsity membership functionthat take complex values for anyThe three membership values and their sum may all lie within the unit circle in the complex plane and this is of the following form:

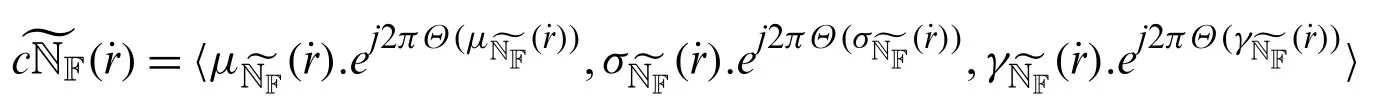
where,

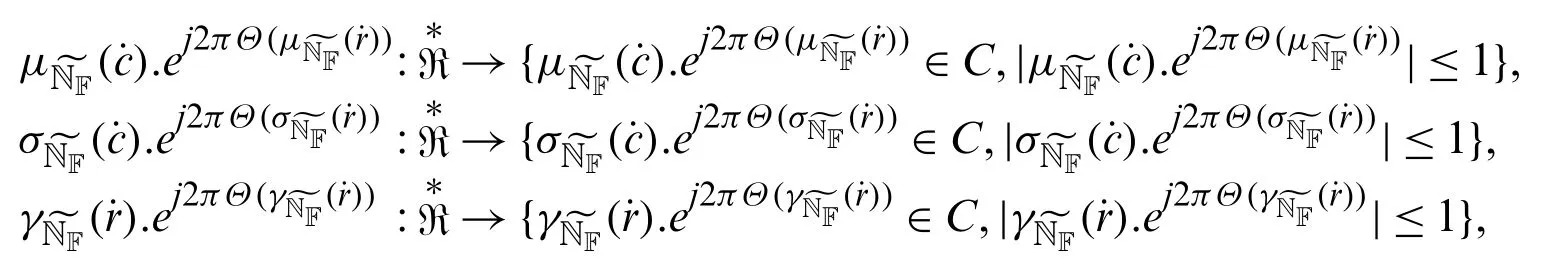
Example 4.1Letbe a universe of discourse.Then,is a complex neutrosophic set ingiven by

4.1 The STOLs of CNSs

The STOLs have been introduced for complex neutrosophic sets and their boundary conditions are verified.

Definition 4.2Letbe a complex neutrosophic number (CNN).

Then,the sine trigonometric operational law of CNNs (ST-OLs-CNNs)is defined as follows:

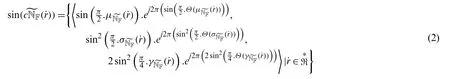
From the above STOL of CNNs,it is evident that the sin()is also a CNN.And it satisfies the following condition of CNSs as the degree of truth,indeterminacy,and false of complex neutrosophic sets are defined,respectively.

Example 4.2Letbe a complex neutrosophic number (CNN).

Then,the sine trigonometric operational law of CNNs (ST-OLs-CNNs)is also a CNN.We describe the function as follows:

Also,the modulus of ST-OLs of CNNs is listed below and it is observed that the sum of values is less than or equal to three.

Then we discuss the fundamental operations on sine trigonometric operational laws of CNNs and their properties.

Definition 4.3[18] Letbe three neutrosophic numbers (NNs)and letbe any scalar.

Then the sine operational laws ofare described below:

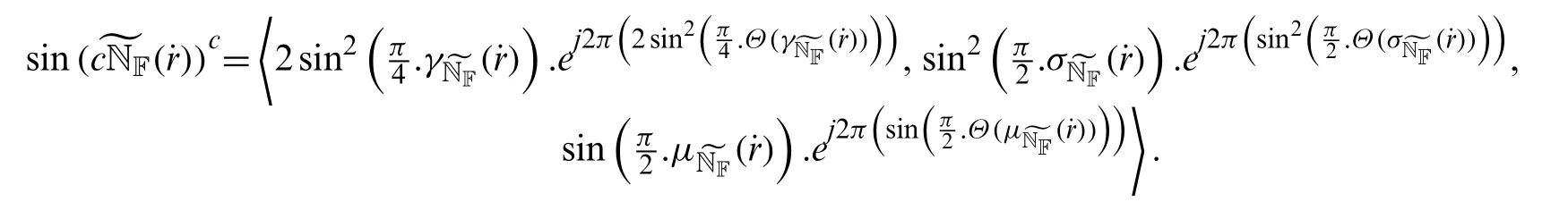
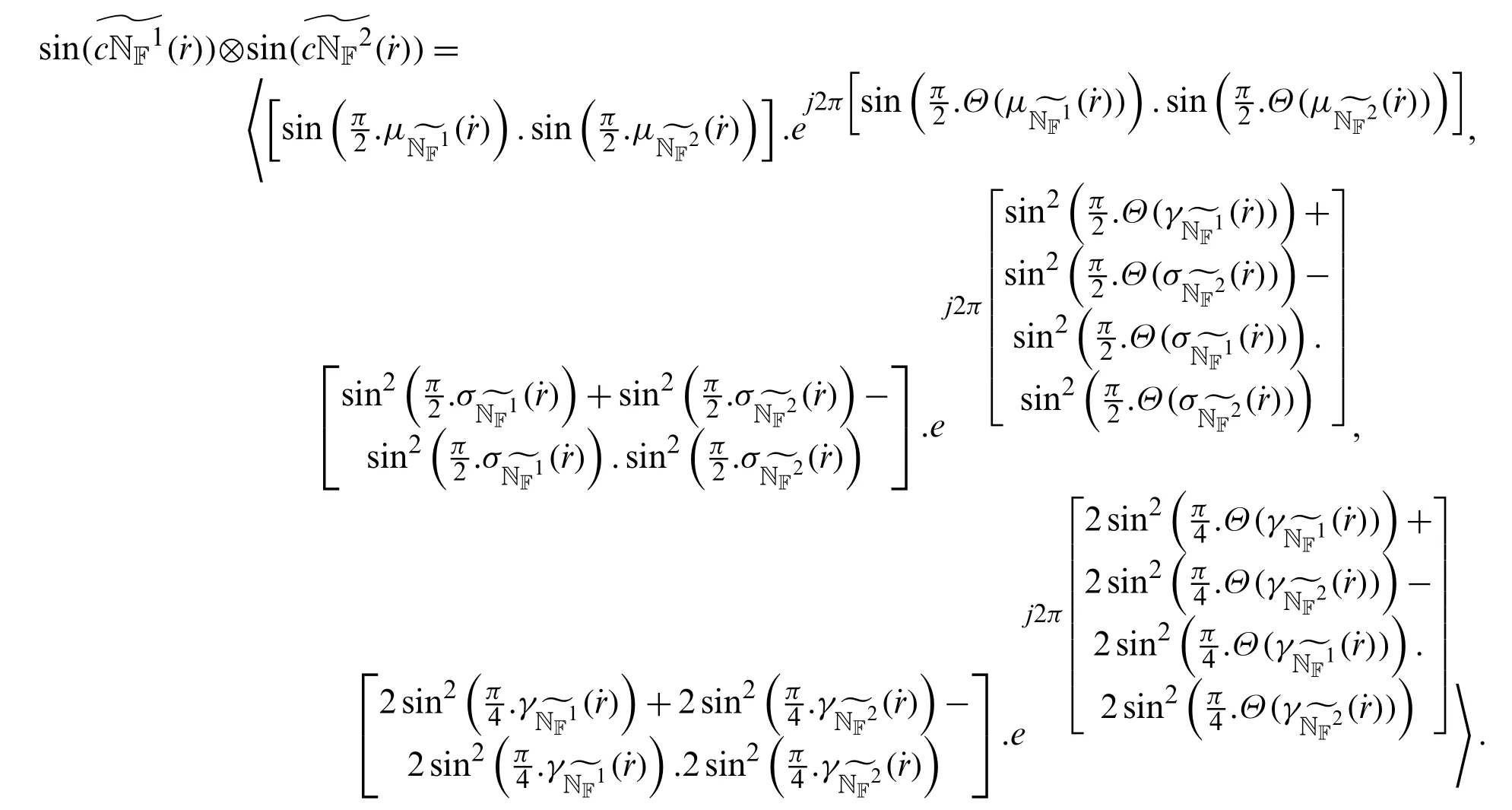
Definition 4.4Letbe sine trigonometric operational law of CNN.

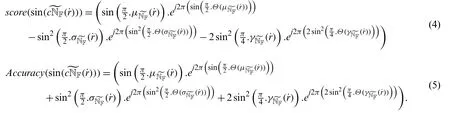
Next,the properties of sine trigonometric operational laws of CNNs are discussed.

Theorem 4.1Letandbe two ST-OL-CNNs.Then,

Proof.The proofs are straightforward from the Definition 4.3.

Theorem 4.2Letandbe two ST-OL-CNNs and k,k1,k2>0.Then,

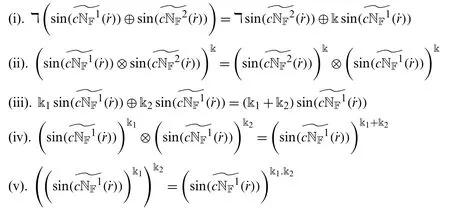
Proof.Letandbe two ST-OL-CNNs;

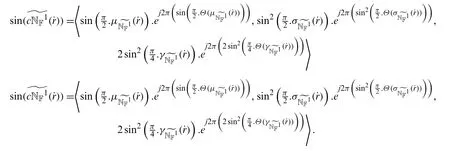
Then,using Definition 4.3 the algebraic sum of two ST-OL-CNNs

(i).For any k>0,then we have

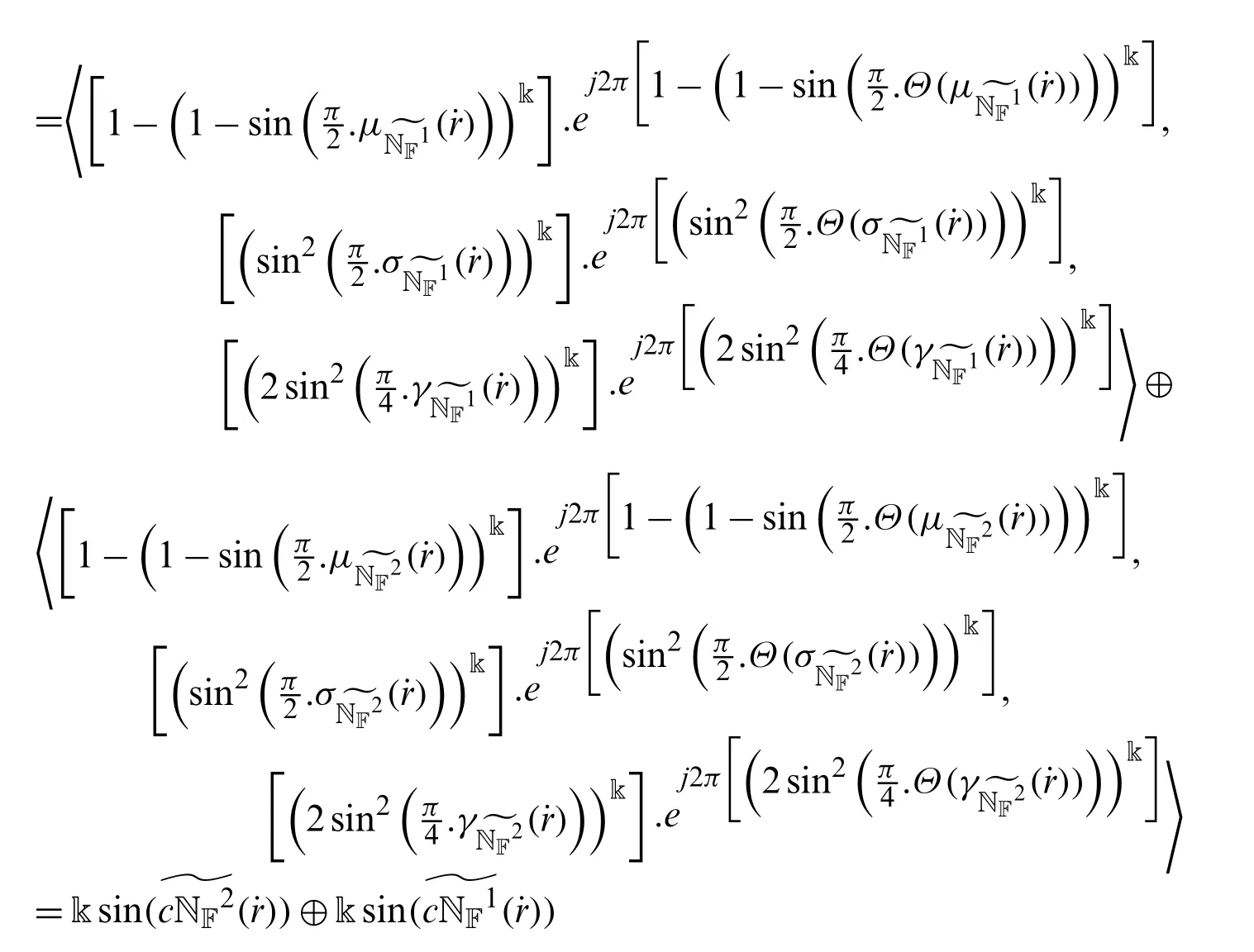
Hence the property (i)is proved.

The proof of property (ii).is similar

(iii).For any k1,k2>0,we have

Hence the proof of property (iii).

Theorem 4.3Letandbe two ST-OL-CNNs such thatandThen

Proof.For any two CNNs

wherei=1,2,we haveSince sin function is increasing in [0,π/2],therefore also we have

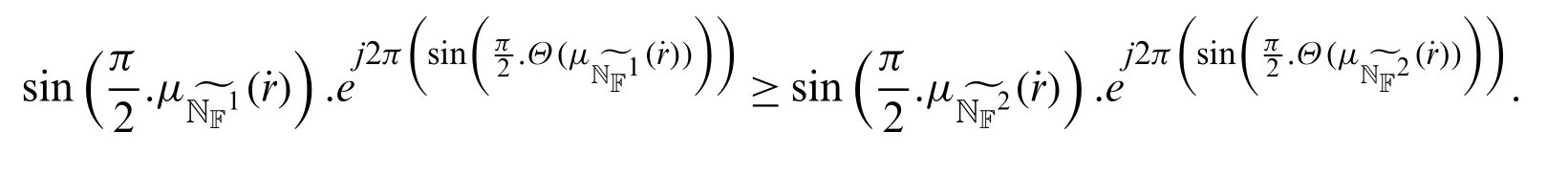
Similarly,for indeterminacy and falsity membership functions.

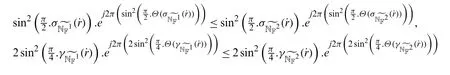
Hence we get from the Definition 4.2 that

4.2 Subtraction of Two Sine Trigonometric CNNs

Definition 4.5Lett=1,2 be two sine trigonometric CNNs mentioned as follows:

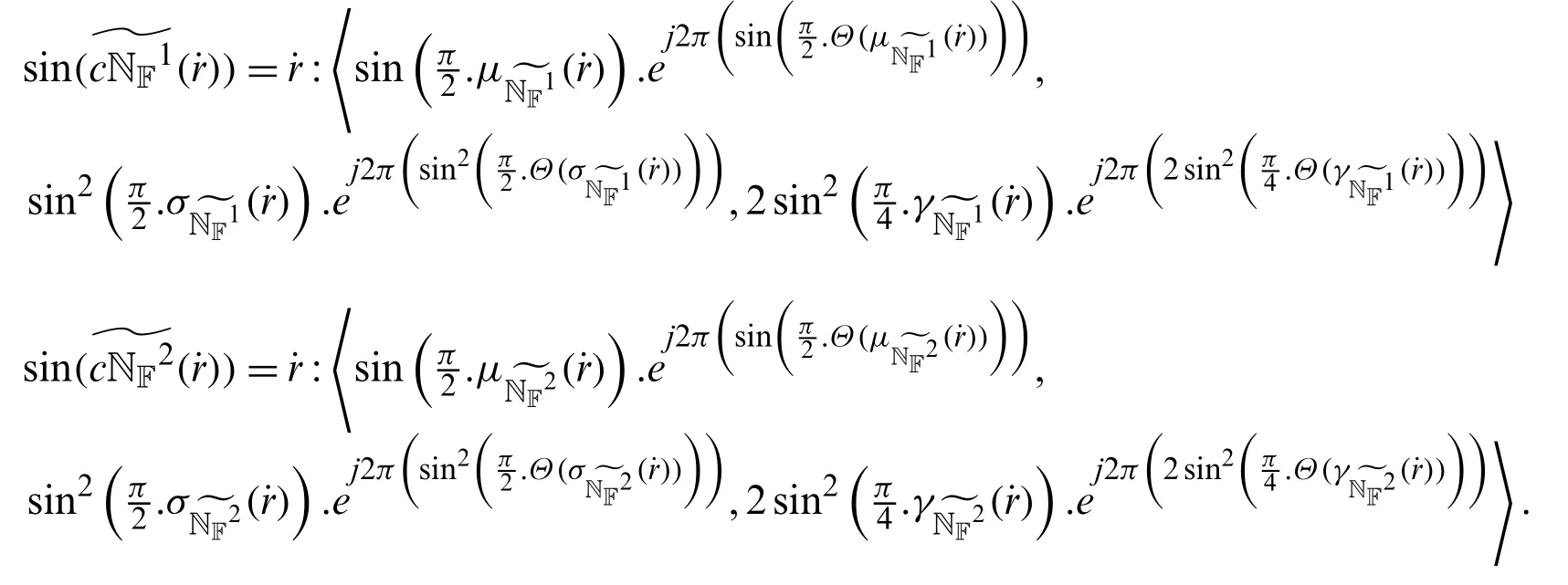
The subtraction is defined as

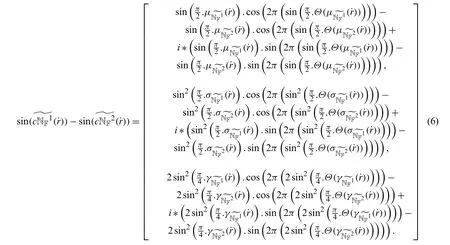
Example 4.3Let two sine trigonometric CNNs be

4.3 Distance Measure of ST-OL-CNNs

In this section,we discuss different types of distance measures of ST-OL-CNNs.

• Whenβ=1 in Eq.(8),it is called the Manhattan distance measure

• Similarly,whenβ=2 Eq.(8),is called the Euclidean distance measure.

Example 4.4Let ST-OLs for two CNNs be given by

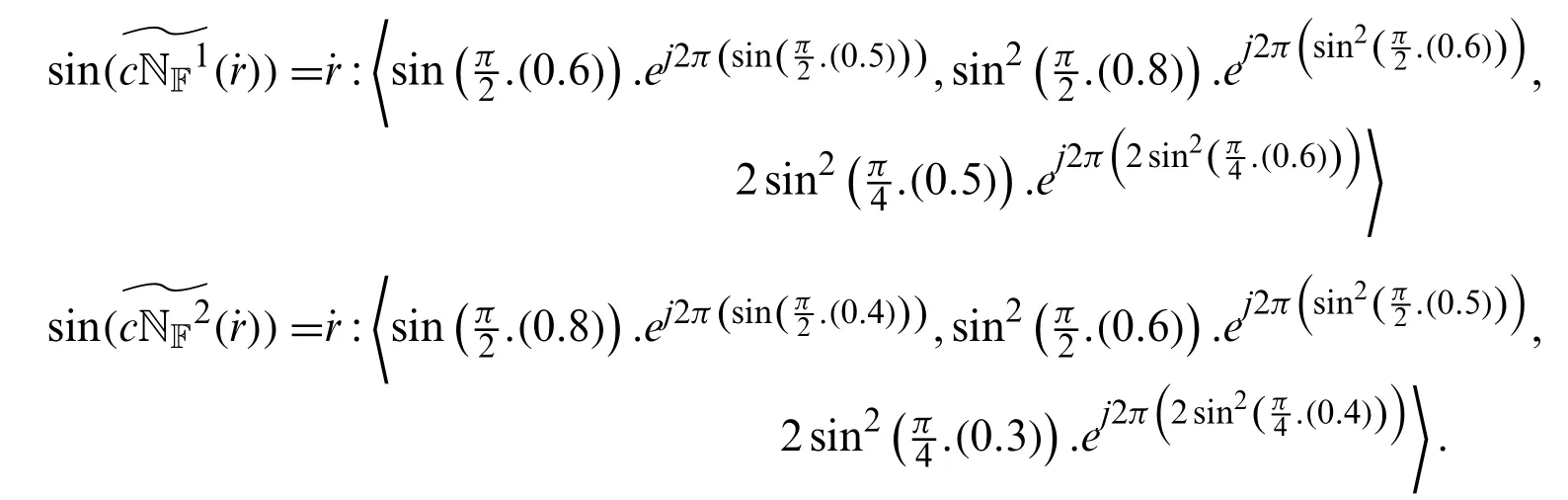
Then,the distance measures are

• Manhattan distance measure (Ma-D):

• Euclidean distance measure (ED):

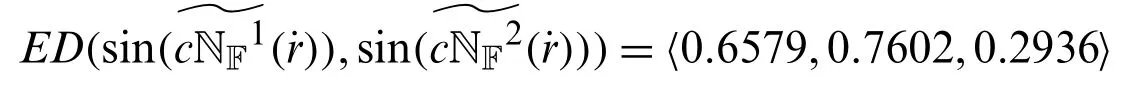
• Minkowski distance measure (MD)whenβ=3:

Note:Here the subtraction of two ST-OL-CNNs is calculated using Eq.(6).

The Minkowski distance measures of ST-OL-CNNs satisfies the following properties:

5 Aggregation Operators for ST-OLs-CNSs

In this section,the weighted averaging and geometric aggregation operators are presented for ST-OLs-CNNs with numerical example.

5.1 Sine Trigonometry Weighted Averaging Aggregation Operator(ST-WAAO)

Definition 5.1Letbe complex neutrosophic numbers (CNNs).

Then the ST-WAAOs for CNNs is denoted byST−WAAO−CNNand defined as follows:

where ðP(P=1,2,...,n)represents the weights ofsuch that ðP≥0 and

Theorem 5.1Letbe CNNs and the weights ofbe such that ðP≥0 andThen theST−WAAO−CNNis defined as follows:

Proof.The proof of Theorem 5.1 is examined by mathematical induction onn.For eachP,(P=1,2,...,n)be CNNs.

Step I.Forn=2,we getST−WAAO−

Using Definition 4.3,the algebraic sum of two ST-OL-CNNsis a CNN.Therefore,ST−WAAO−is also a CNN.Further,

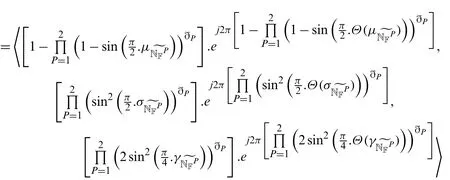
Step II.Suppose that Eq.(10)holds forn=κ,

Step III.Next,we have to prove that Eq.(10)holds forn=κ+1,

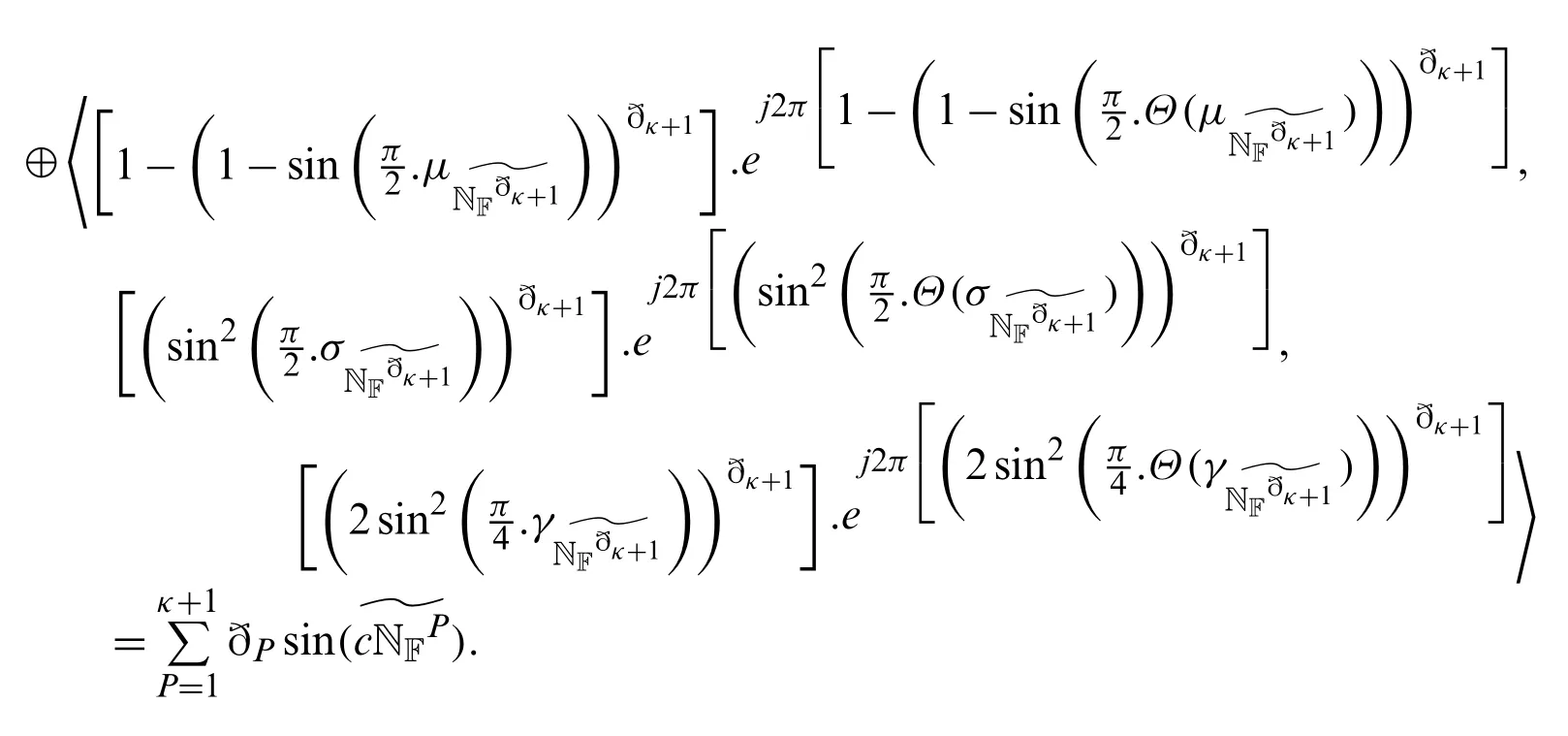
Hence the proof.

Example 5.1Suppose that=〈0.5ej2π(0.7),0.6ej2π(0.5),0.5ej2π(0.4)〉,=〈0.5ej2π(0.7),0.7ej2π(0.5),0.2ej2π(0.4)〉,=〈0.8ej2π(0.7),0.4ej2π(0.6),0.6ej2π(0.5)〉 are CNNs and the corresponding weights are given respectively as ð1=0.4,ð2=0.35,ð3=0.25.Then the value ofST−WAAO−CNNis calculated as follows:

Then absolute value of ST-WAAO-CNN is calculated as follows:ST−WAAO−=〈0.8127,0.5969,0.1706〉

Next,we give some properties of the ST-WAAO-CNNs operator and establish that they preserve idempotency,boundedness,monotonically,and symmetry.

Theorem 5.2Let(P=1,2,...,n)be CNNs such thatThenST−WAAO−

Proof.LetBy Theroem 5.1,we get

Hence proved.

Theorem 5.3Let(P=1,2,...,n)be CNNs and

Proof.For anyP,

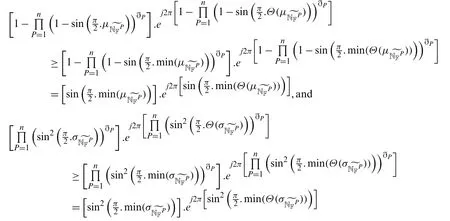
similarly,

Also,we have

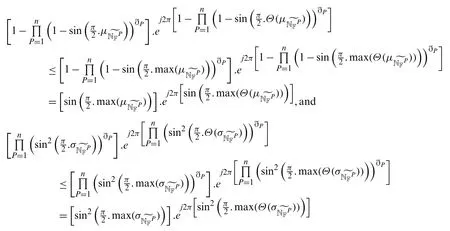
similarly,

Theorem 5.4Letbe two collections of CNNs.

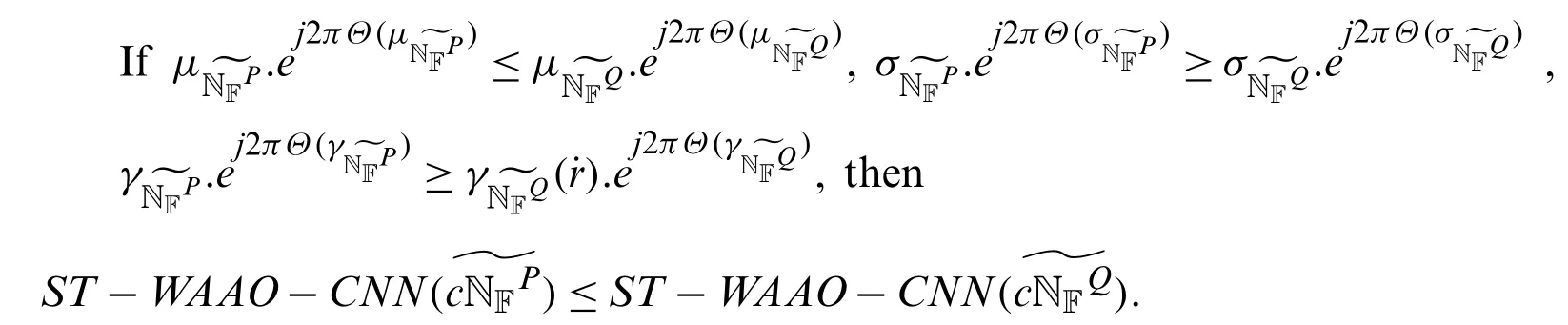
Proof.It follows from Theorem 5.3 and hence the proof is omitted.

Theorem 5.5Let(P=1,2,...,n)andbe two collections of CNNs.Then

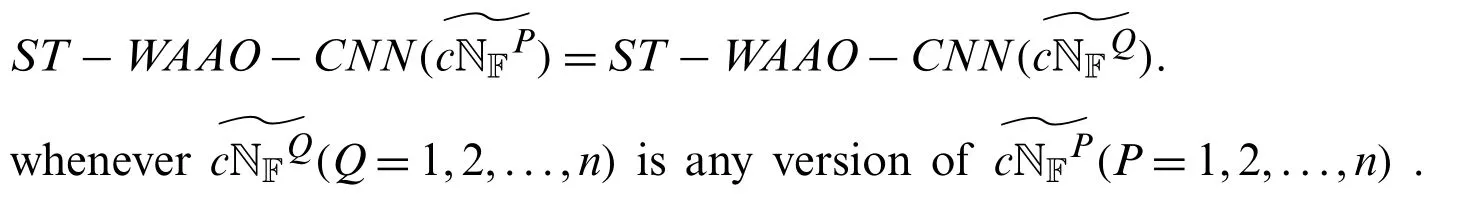
Proof.The proof follows from Theorem 5.3.

5.2 Sine Trigonometry Weighted Geometric Aggregation Operator(ST-WGAO)

Definition 5.2Let;P=1,2,...,nbe complex neutrosophic numbers (CNNs).

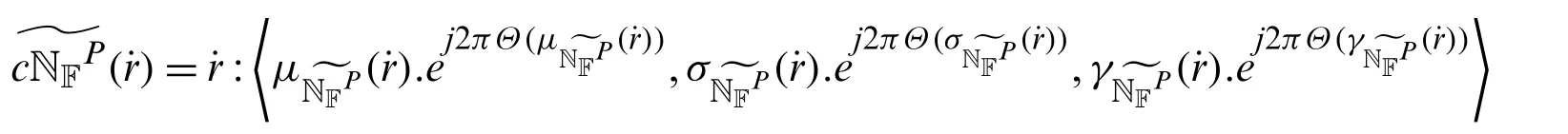
Then the ST-WGAOs for CNNs is denoted byST−WGAO−CNNand defined as follows:

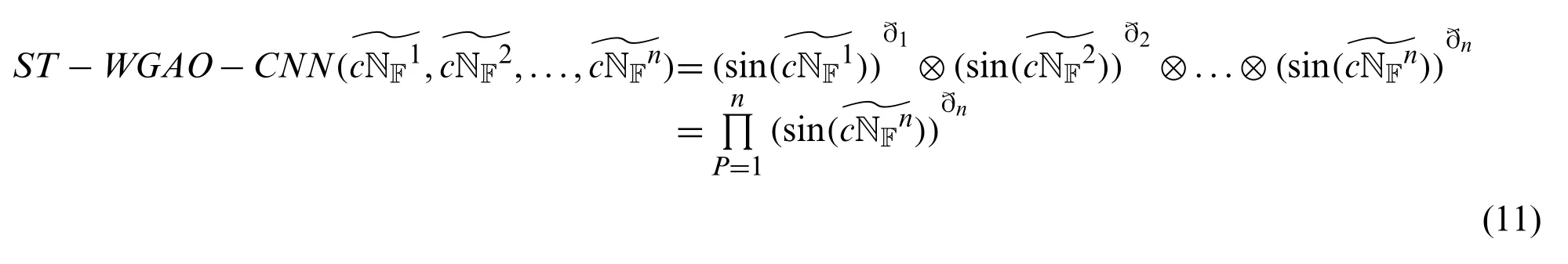
where ðP(P=1,2,...,n)represents the weights ofsuch that ðP≥0 and

Theorem 5.6Let(P=1,2,...,n)be CNNs and the weights ofbe represented by ðP(P=1,2,...,n)such that ðP≥0 andThen theST−WGAO−CNNis definedas follows:

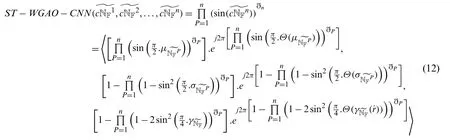
Proof.The proof of theorem 5.6 is examined by mathematical induction onn.For eachP,(P=1,2,...,n)be CNNs.Then the following steps are involved.

Step I.Forn=2,we getST−WGAO−

Using Definition 4.3,the algebraic product of two ST-OL-CNNsis a CNN.Therefore,ST−WGAO−is also a CNNs.Further,

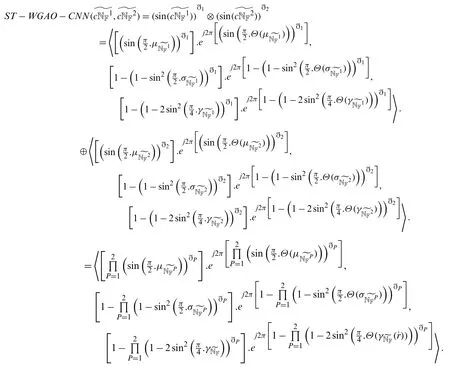
Step II.Suppose that Eq.(12)holds forn=κ,

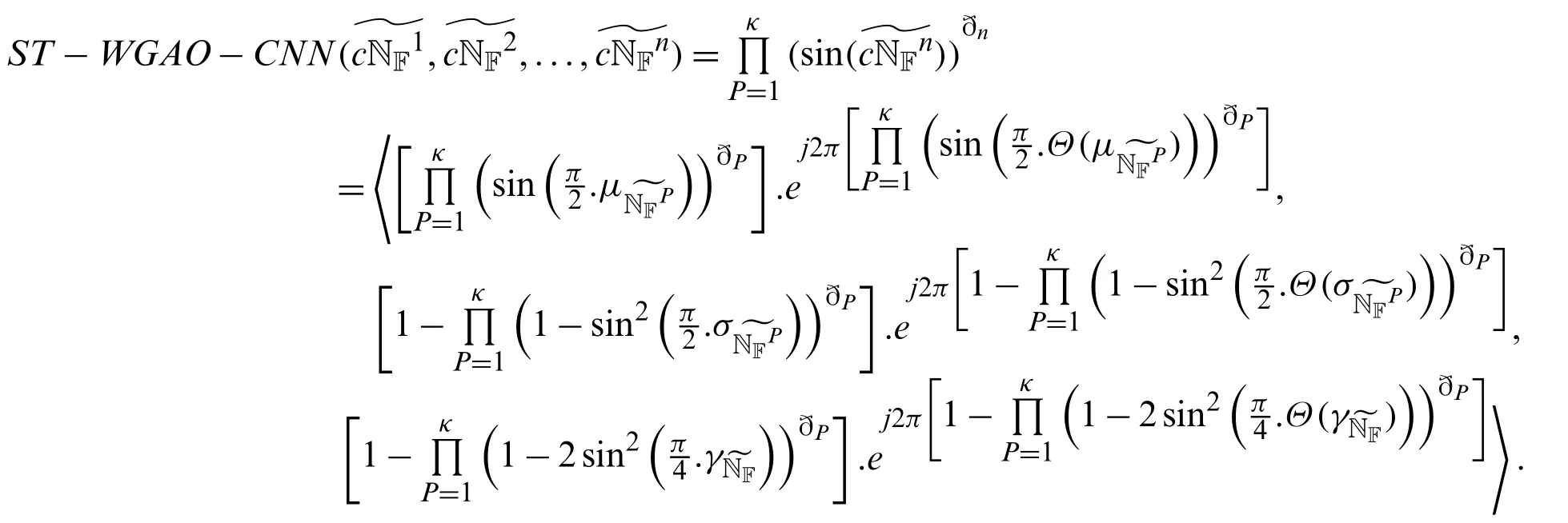
Step III.Next,we have to prove the Eq.(12)holds forn=κ+1,

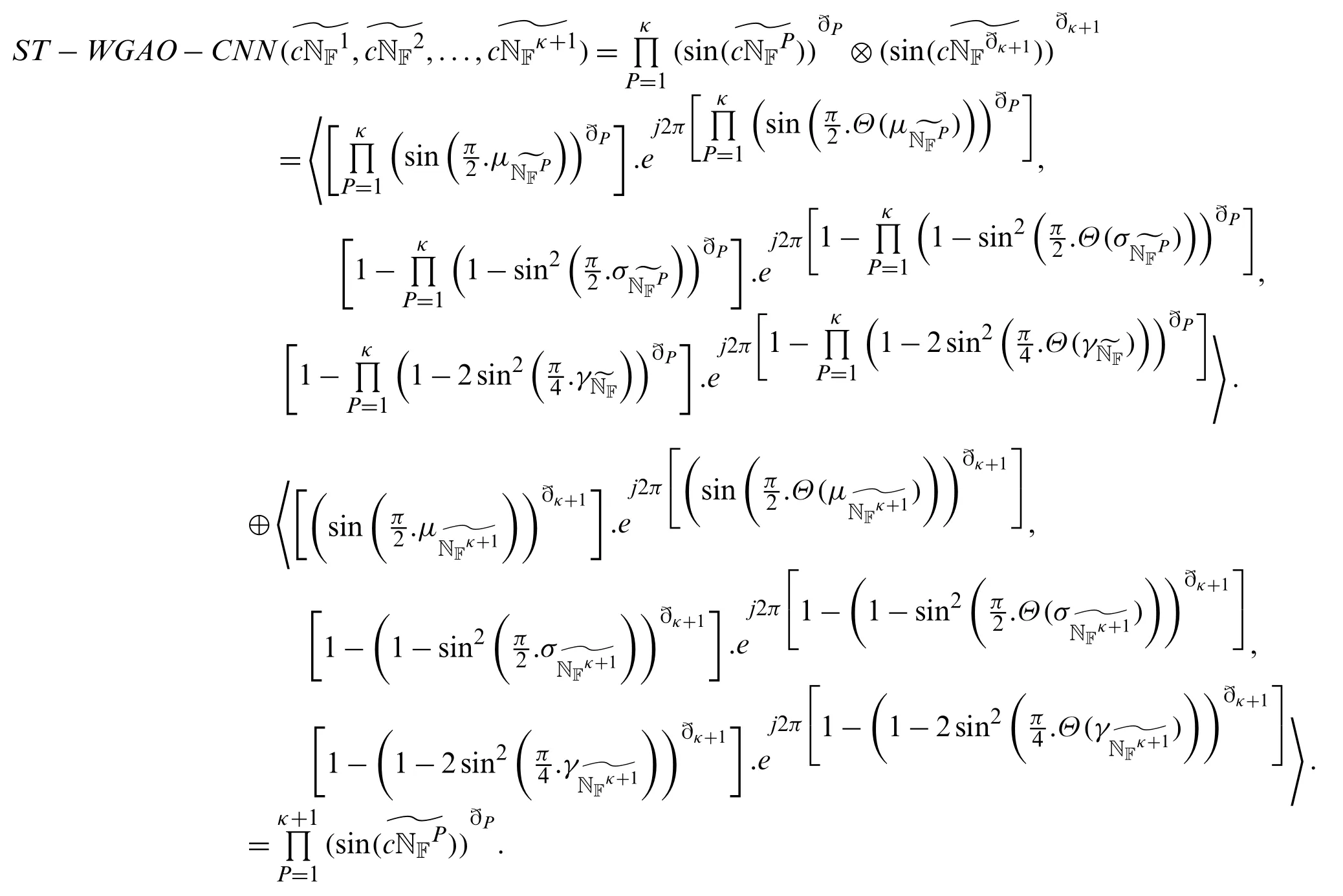
Hence the proof.

Example 5.2Let= 〈0.5ej2π(0.7),0.6ej2π(0.5),0.5ej2π(0.4)〉,= 〈0.5ej2π(0.7),0.7ej2π(0.5),0.2ej2π(0.4)〉,=〈0.8ej2π(0.7),0.4ej2π(0.6),0.6ej2π(0.5)〉 be CNNs and the corresponding weights are given respectively as ð1=0.4,ð2=0.35,ð3=0.25.Then the value ofST−WGAO−CNNis calculated as follows:

Then absolute value of ST-WGAO-CNN is calculated as follows:ST−WGAO−=〈0.7615,0.6617,0.2510〉.

Theorem 5.7Let(P=1,2,...,n)be CNNs such that(P=1,2,...,n)=.Then

Theorem 5.8Letbe CNNs and

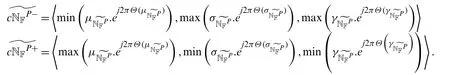
Theorem 5.9Letandbe two collections of CNNs.

Theorem 5.10Letbe two collections of CNNs.Then

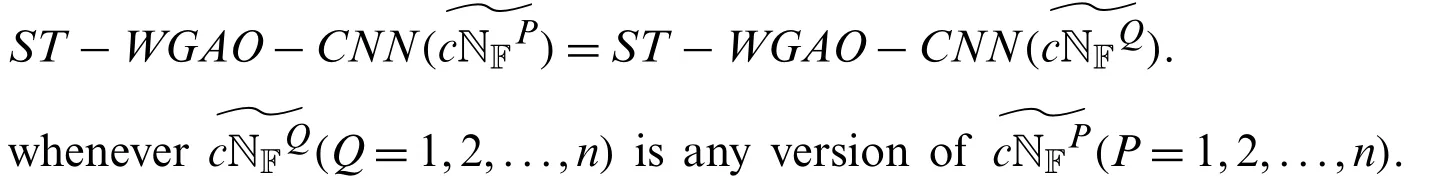
The proof of above all theorems 5.7-5.10 follow from Theorems 5.2-5.5 directly.

5.3 Fundamental Properties of ST-AOs for CNNs

Theorem 5.11Letare two collections of CNNs.Then we have

Proof.Sincebe two collection of CNNs.By Definition 4.3

As for anyα,β≥0,.β⇒α+β−α.β≥α.β⇒1 −(1 −α).(1 −β)≥α.β.

Thus,by takingα=we have

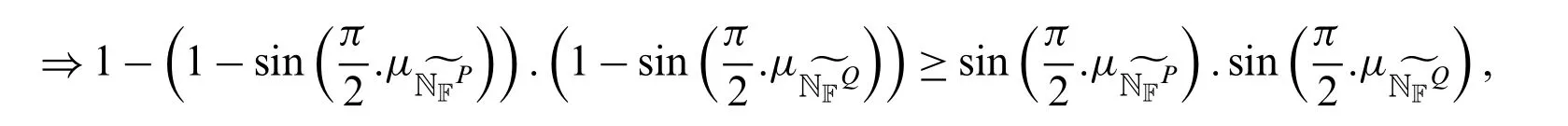
which implies

Similarly,

Theorem 5.12Letbe CNNs and for any ðP≥0,

(1)ðP

(2)ðP

Proof.The proof of the theorem follows from Theorem 5.11.

Theorem 5.13Letbe CNNs,then

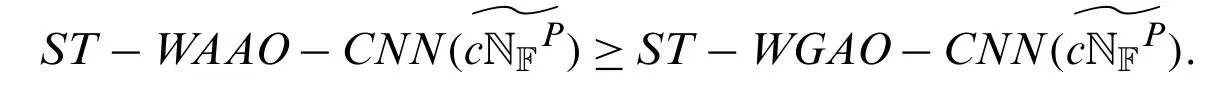
Here the equality holds if and only if

Proof.The proof of the theorem follows from Theorem 5.11.

6 Decision Making Techniques

This section presents a decision making technique that could be utilized to solve uncertain multi criteria decision making (MCDM)problems with complex neutrosophic information.MCDM problems can be handled by decision matrix,in which all elements are represented in terms of ST-OLs-CNNs with respect to alternatives over criteria/attributes by decision makers.Thus,a decision matrixMi×j,consists ofnnumber of alternatives(Ł1,Ł2,...,Łn)andmnumber of criteria/attributes(B1,B2,...,Bm).The unknown weight vector of each criterion is denoted by(ð1,ð2,...,ðm)which could be calculated by entropy method.

Suppose that the complex neutrosophic decision matrix (ST-Ols-CNDM)is denoted byMi×j,

where all elements are ST-OLs-CNNs ∀i=1,2,...,n,j=1,2,...,m.The decision making algorithm is described in the following steps:

Step 1.The collected vague data are transformed to ST-OLs-CNNs(M)

Step 2.Construct the normalized complex neutrosophic decision matrixM∗=[]m×nfromM=[λij]m×n,

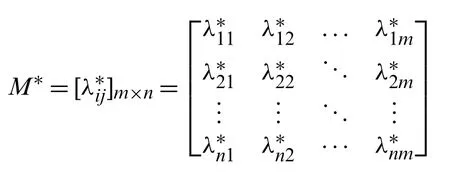
whereis computed by the following conditions

Ifλijis benefit type criteria/attributes

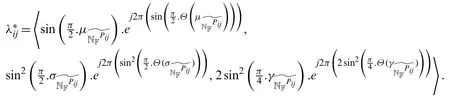
Ifλijis cost type criteria/attributes

Step 3.The weights of the criteria/attributes are unknown.So the entropy principle 6.1 is used to calculate the weights of criteria/attributes(ð1,ð2,...,ðm).

Step 4.From the normalized decision matrixM∗=[λ∗ij]m×nand the criteria weight vector(ðj),the fused information of each alternative are obtained by either ST-WAAO-CNN (Eq.(10))or ST-WGAO-CNN (Eq.(12)).

Step 5.Calculate the score value of each aggregated value.

Step 6.Rank the alternatives according to their absolute score values.

6.1 Entropy Method

Shannon proposed the theory of entropy [42],which is a measure of uncertainty in information represented in terms of probability theory.To evaluate relative weights,Shannon’s entropy approach interprets the relative intensities of the criterion based on the discrimination among data.The steps in the shannon’s entropy approach are as follows:

Step(i).The complex neutrosophic decision matrix [M]′∀i=1,2,3,...,m,j=1,2,3,...,nis formed:

Step (ii).Utilize score function to initial ST-Ols-CN decision matrix [M]′and find secondary score decision matrix [M]′′where the elements(λ′′ij)are complex fuzzy numbers

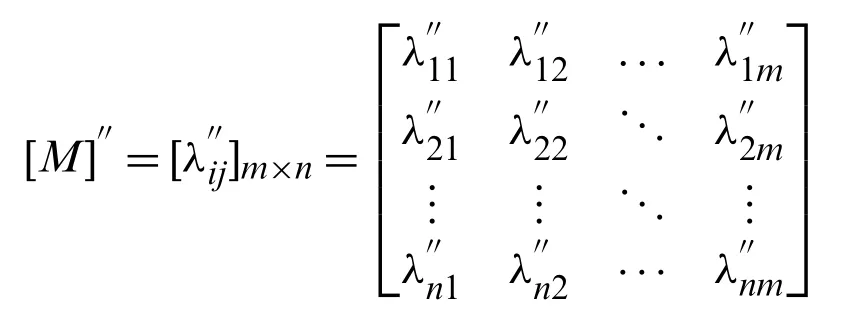
Step(iii).Then,normalize the secondary decision matrix

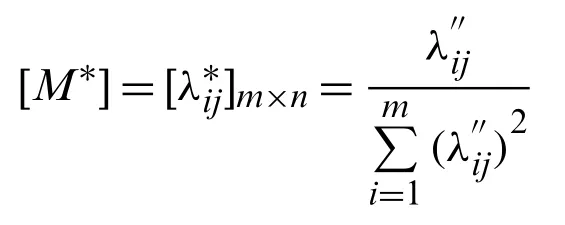
Step(iv).Calculate the entropy of each criterion

Step(v).Calculate the variation coefficient of criterionCj

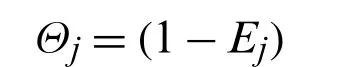
Step(vi).Determine the weight of each criterionCjby the following equation:

7 Application of the Proposed ST-OLs-Complex Neutrosophic Decision Making Approach

The selection of materials for industry plays an essential role in their functioning.Also,the growing material availability in the world has created a variety of options.But,very less attention has been given to tools and methods that facilitate material selection process.In addition,this process needs to consider multiple properties depending on tools/method requirements to make a better decision.For manufacturers and engineers,it is a crucial and challenging task to select best sustainable option from a number of materials used in the modern industry and many factors are involved in such decision making process.MCDM approaches are more efficient in the selection process of materials.Khandekar et al.[43] utilized decision making approach based on fuzzy axiomatic design principles for material selection.Mayyas et al.[44] implemented fuzzy TOPSIS method to select best eco-material.A fuzzy logic based PROMETHEE method have been used for material selection problems by Gul et al.[45].Using TOPSIS approach with some popular normalization methods Yang et al.[46] proposed an efficient method for material selection.A systematic review on material selection methods have been explained in detail by Rahim et al.[47].

Case Study.A manufacturing company is planning to buy materials(Ł1,Ł2,...,Łn)from suppliers based on four criteria namelyB1-Cost,B2-Quality and efficiency of the material,B3-Demand,B4-Availability of the material.Usually in the complex neutrosophic numbers,the amplitude values lie between zero and one that represent the initial intuition values of material over criteria and the phase terms represent the secondary intuition values after a certain interval of time.Through this process,a decision maker evaluates the alternatives (Materials)under these criteria and gives his preference values in CNNs which are given in Tables 1 and 2.Then the weights of criteria are calculated based on entropy approach and demonstrated numerically in the following Subsection 7.1:

Step 1.The formation of ST-OLs-complex neutrosophic decision matrix that is Table 2 is derived from usual complex neutrosophic decision matrix (Table 1).

Step 2.All the criteria are benefit type.The normalized ST-OLs of complex neutrosophic decision matrixM∗=[λ∗ij]m×nis taken from Table 2.

Step 3.The weights of the criteria/attributes are unknown.So the entropy principle 6.1 has been used to calculate the following weights of criteria/attributes.ð1=0.9242+0.1193j,ð2=0.2403 −0.0083j,ð3=−0.1081 −0.0143j,ð4=−0.0564 −0.0967j

Step 4.From the normalized decision matrixM∗,i.e.,Table 2 and the criteria weight vector(ðj),the fused information of each alternative are obtained obtained using ST-WAAO-CNN(Eq.(10))and given in Table 3.

Step 5.The score values of each alternative are given below:Ł1=0.964 −0.824j,Ł2=0.311+0.077j,Ł3=−0.175 −1.412j,Ł4=−0.029 −0.627j,Ł5=−0.798 −0.427j

Step 6.The ranking order of the alternatives according to their amplitude values is listed as follows:

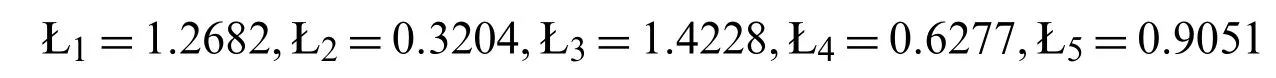
Similarly,Using ST-WGAO-CNN (Eq.(12))operator,the aggregated complex neutrosophic decision matrix is obtained and is shown in Table 4;

Table 1:Complex neutrosophic decision matrix

The score value of each alternative are given below:

Ł1=1.2199 −0.8039j,Ł2=0.5097+0.3345j,Ł3=−0.0203 −1.5088j,

Ł4=−0.1867 −0.8343j,Ł5=−1.0583+0.5679j

The ranking order of the alternatives according to their amplitude values is listed as follows:

Ł1=1.4610,Ł2=0.6097,Ł3=1.5089,Ł4=0.8549,Ł5=1.2010

Then,the ranking order is Ł3≻Ł1≻Ł5≻Ł4≻Ł2.

7.1 Calculation of Entropy Based Criteria Weights

These are the following steps involved in the Shannon’s entropy method to calculate the criteria weights;

Step(i).The initial complex neutrosophic decision matrix [M]′is considered from Table 2.

Step(ii).Using score function to initial ST-Ols-CN decision matrix [M]′,we get the secondary score decision matrix [M]′′where all elements(λ′′ij)are complex fuzzy numbers as mentioned in Table 5.

Table 2:ST-OLs-complex neutrosophic decision matrix [M]

Table 3:The aggregated complex neutrosophic decision matrix (Mo)

Table 4:The aggregated ST-OLs-complex neutrosophic decision matrix (Mo)

Step(iii).The normalization of the secondary decision matrix [M∗] is given in Table 6.

Table 5:ST-OLs-complex neutrosophic secondary score decision matrix [M′]

Table 6:The normalized decision matrix [M∗]

Step(iv).The entropy of each criterion is given as follows:E1=1.0423+2.0489j,E2=1.0966+0.5198j,E3=0.9958 −0.2397j,E4=1.1919 −0.1543jwhere,

Step (v).The variation coefficient of each criterion(Cj)is calculated byΘj=(1 −Ej).The values are

Θ1=−0.0423 −2.0489j,Θ2=−0.0966 −0.5198j,Θ3=−0.0042+0.2397j,Θ4=−0.1919+0.1543j

Step(vi).Finally,the weight of each criterionCjare calculated using Eq.(13)

ð1=0.9242+0.1193j,ð2=0.2403 −0.0083j,ð3=−0.1081 −0.0143j,ð4=−0.0564 −0.0967j.

Note:The result satisfies the property that the sum of all complex weights is equal to one.That means

(0.9242+0.1193j)+(0.2403 −0.0083j)+(−0.1081 −0.0143j)+(−0.0564 −0.0967j)=1.0000+0.0000j

8 Validation of the Proposed Method

The proposed concept of sine trigonometry operational laws of complex neutrosophic decision making approach is verified with entropy based combinative distance-based assessment (CODAS)method.A decision matrix,i.e.,Table 2 has been taken for entropy-CODAS method.In the initial process,criteria weights are derived using the steps given in Section 6.1.And the weight values are calculated and given as follows; ð1=0.9242+0.1193j,ð2=0.2403 −0.0083j,ð3=−0.1081 −0.0143j,ð4=−0.0564 −0.0967j.The steps of entropy based CODAS method as mentioned in the literature by Ghorabaee et al.[48] is demonstrated numerically for ST-OLs-CNNs as follows:

Step 1.The ST-OLs-CN decision-making matrix is considered as in Table 2

Step 2.Each element in ST-OLs-CN decision matrix is normalized by the following linear normalization Eq.(14)

Step 3.The ST-OLs-CN weighted normalized decision matrix is calculated byλ∗ij.ðj,where ðjdenotes the complex weights of each criterion such that 0 ≤ðj≤1.0000+0.0000j.

Step 4.The ST-OLs-CN negative-ideal solution of the weighted normalized decision matrixis given in Table 7.

Step 5.The Euclidean and Taxicab distances of alternatives from the ST-OLs-CN negativeideal solution are calculated by Eqs.(15)and (16)

The values are shown in Tables 8 and 9.

Step 6.The relative assessment of ST-OLs-CN matrix is derived from Eq.(17),and shown as in Table 10.

Table 7: N−j (ST-OLs-CN negative-ideal solution)

Table 8:Euclidean distances from N−j

Table 9:Taxicab distances from N−j

whereψdenotes a threshold function used to recognize the equality of the Euclidean distances of two alternatives,and is defined as follows:

τis the threshold parameter that can be set by decision-maker.It is better that this parameter be a value between 0.01 and 0.05.Here,theτvalue is 0.01.

Step 7.The assessment value of each alternative is obtained by Eq.(19)

The values obtained are shown in Table 11.

Table 10:The relative assessment ST-OLs-CN matrix

Table 11:The assessment value of each alternative Hi

Step 8.Using ST-OLs-CN score function,the score of eachHiis calculated as follows:

Ł1=−2.2613 −7.3637i,Ł2=−0.1610+6.4493i,Ł3=−11.5005 −5.1971i,

Ł4=−3.1753 −2.1815i,Ł5=2.1245 −2.4657i

Then,the absolute values of the above mentioned ST-OLs-CN score values are given as

Ł1=7.7031,Ł2=6.4513,Ł3=12.6203,Ł4=3.8524,Ł5=3.2547.

Step 9.Rank the alternatives according to the absolute values

Ł3>Ł1>Ł2>Ł4>Ł5

8.1 Discussion and Comparison Analysis

The outcomes of the new and existing techniques are compared in Table 12 to demonstrate the validity of the proposed approach.It is transparent that the optimal alternative is the same for all techniques.As a result,the proposed concept of sine trigonometric operational laws of complex neutrosophic sets performs better in complex decision-making procedures.But,this operator can handle only the particular types of uncertainty which have periodicity in the form of amplitude and phase terms to the three membership functions such as truth,indeterminacy and falsity where amplitude represents the real valued membership functions and an additional term called phase represents periodicity.In this research,the execution of multi-criteria decision making approach their results in complex numbers.So,in order to select the best among them we have to consider the absolute values.

Table 12:The ranking order of each alternatives

9 Conclusion

In this study,a decision making method with sine trigonometric operational laws for complex neutrosophic fuzzy sets have been proposed.The operations of ST-OLs-CNNs play a vital role during the decision making process and with help of these operations some of the ST-OLs-CN aggregation operators have been developed in order to make decision over complex vague information.The description of ST-OLs have been given with CNNs in detailed graphical representation and it shows the validity of the ST-OLs.The properties of the proposed sine trigonometric weighted AOs are proved.Further,in the proposed MCDM method,the criteria weights are computed by unsupervised techniques and by combining these methods a new approach called Entropy-ST-OLs-CNDM method has been introduced.Then the functionality of the proposed method is applied to a material selection problem and,feasibility and validity of the approach are investigated in detail with comparative analysis.

In future research,advanced study of the similarity measures of complex neutrosophic sets and complex neutrosophic critic-based approach for handling MCDM problems with unknown weights can be carried out.The recommended approach can also be applied to other fields,such as medical nutrition diagnostics,sustainable supplier selection,and so on.

FundingStatement:This work was supported in part by the Rajamangala University of Technology Suvarnabhumi.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.