Thermogram Adaptive Efficient Model for Breast Cancer Detection Using Fractional Derivative Mask and Hybrid Feature Set in the IoT Environment

Ritam Sharma,Janki Ballabh Sharma,Ranjan Maheshwari and Praveen Agarwal

1Rajasthan Technical University,Kota,Rajasthan,324010,India

2Anand International College of Engineering,Jaipur,303012,India

3Nonlinear Dynamics Research Center(NDRC),Ajman University,Ajman,20550,United Arab Emirates

4International Center for Basic and Applied Sciences,Jaipur,302029,India

5Institute of Mathematical Modeling,Almaty,050000,Kazakhstan

ABSTRACT In this paper,a novel hybrid texture feature set and fractional derivative filter-based breast cancer detection model is introduced.This paper also introduces the application of a histogram of linear bipolar pattern features(HLBP)for breast thermogram classification.Initially,breast tissues are separated by masking operation and filtered by Gr¨umwald-Letnikov fractional derivative-based Sobel mask to enhance the texture and rectify the noise.A novel hybrid feature set using HLBP and other statistical feature sets is derived and reduced by principal component analysis.Radial basis function kernel-based support vector machine is employed for detecting the abnormality in the thermogram.The performance parameters are calculated using five-fold cross-validation scheme using MATLAB 2015a simulation soたware.The proposed model achieves the classification accuracy,sensitivity,specificity,and area under the curve of 94.44%,95.55%,92.22%,96.11%,respectively.A comparative investigation of different texture features with respect to fractional order α to classify the breast malignancy is also presented.The proposed model is also compared with a few existing state-of-art schemes which verifies the efficacy of the model.Fractional order α offers extra adaptability in overcoming the limitations of thermal imaging techniques and assists radiologists in prior breast cancer detection.The proposed model is more generalized which can be used with different thermal image acquisition protocols and IoT based applications.

KEYWORDS Thermal image; breast cancer; fractional derivative mask; image texture analysis; feature extraction; radial basis function; machine learning

1 Introduction

Breast cancer has become a widely occuring disease among women and the reason of rapidly increasing death rate due to its late diagnosis [1].Breast cancer is caused by a genetic mutation of Deoxyribonucleic acid (DNA)in the cells of breast tissues and these cells keep reproducing the same muted cells.These abnormal cells cluster together to form a tumor which becomes cancerous when these abnormal cells metastasize to rest of the body parts through the bloodstream or lymphatic system [2].The most significant factors of developing breast cancer are advancing age and inheritance [3].Therefore,early and accurate screening of breast cancer offers a major role in treating breast malignancy and reducing the mortality rate.

There are various screening techniques which aim at an early revelation of breast disease.These techniques depend on light,sound,heat,X-ray,nuclear,magnetism,microwave,and fusion of different methods.Among these techniques,digital mammography is believed to be the gold standard and widely used technique for tumor detection and classification [4].But mammography shows low sensitivity (true positive)with high specificity (true negative)whereas Magnetic Resonance Imaging (MRI)reveals high sensitivity with reduced specificity for premature detection of breast cancers [5].Also,the patients must bear intense pain during the process of mammography.Thus,the limitations of present screening and diagnostic modalities necessitate the development of an advance and more effective technique with higher sensitivity and specificity for premature stage breast cancer detection [6].

Thermography has immense potential for screening breast diseases as it has already been reported that breast disease can be detected decay prior to the conventional technique like mammography [2].Thermography is an unobtrusive,contactless,painless,radiation-free,temperature screening imaging technique.It is being regarded as a consistent add-on tool nowadays with high sensitivity and specificity [5].Most of the breast cancer screening techniques focus on finding the tumor or cancerous regions by detecting physical changes in cell structures,but,thermal imaging has the potential in finding the thermal disruption due to functional changes in the cells which helps in investigating the presence of pre-stage of early cancer [6,7].It has already been reported that clinically healthy breast tissues have predictable and regular heat patterns on the skin surface while unhealthy breast tissues have irregular heat patterns due to physiological processes such as vascular disturbances and inflammation [1-3].

Thermal patterns emitted by human skin are recorded by a thermal camera and a heat signature is generated called the thermogram [5].But the thermograms alone are not adequate for clinical experts to make an exact diagnosis,so some expository tools,for example,bio-measurable strategies,automation of the different steps involved in the procedure,artificial intelligence,or computer vision techniques are required to assist and analyze the thermograms objectively.In this regard,several computer-aided diagnosis schemes have been developed to detect the disease accurately [6].

Most of the computer-aided schemes reported in the literature have performed bilateral asymmetry analysis which limits the performance for the cases where malignancies closely resemble in both breasts [7].The detection accuracy of such schemes is reliant on the difference between features of left and right breast tissues.Since thermograms are low-intensity images with small signal-to-noise ratio therefore the detection accuracy may be limited and the false negative detection rate may be higher [8,9].However,many schemes reported in literature have also analyzed each breast separately to overcome the above limitation [10,11].Such schemes may suffer from the problem of false positive error if the selection of feature and feature quality is not proper.Therefore,selection of features and feature quality play a vital role as one kind of feature may not suit other imaging modalities.

In thermogram-based breast cancer detection schemes reported in the literature,statistical,Gabor,HOG,etc.,texture features have been exploited to improve the detection accuracy [9-15].But,the comparative performance evaluation of popular texture feature sets is missing in the literature.Secondly,bias correction and image registration are required in thermograms due to misalignment and inconsistency in the acquisition process.Any inaccuracy in these operations directly affects the performance of cancer detection.Recently,a number of fractional-order mathematical models have been developed for analyzing and treating various diseases [16-18].Fractional derivative-based filtering has shown its suitability in overcoming the above problems due to its tuning parameter (fractional order parameter)and also enhancing the low-intensity texture [19].Also,the effect of fractional derivative filters on computer-aided breast cancer detection schemes using thermogram has not been reported yet.

Therefore,within this paper,a computer-aided breast cancer or malignancy detection model using thermograms is presented which processes breast tissues (non-asymmetry based)using fractional derivative-based Sobel filter.The comparative performance of different popular texture feature sets is also performed with respect to fractional derivative order parameter alfa (α).This parameter alfa provides an additional degree of flexibility in compensating errors.Moreover,a hybrid feature set is also derived and compared.The comparative analysis shows its superiority over the other feature sets.The major contributions of this paper are:

• A new hybrid feature set is derived by combining different feature sets and analyzed for breast cancer detection.

• This paper introduces a histogram of linear bipolar pattern features (HLBP)for breast thermogram classification.

• Comparative analysis of thermogram texture features used for breast cancer classification is also presented,which aids the literature.

• A fractional derivative-based Sobel filter is applied for texture enhancement,noise reduction,and providing robustness against variations and degradations in thermograms.It also offers the vitality of optimizing the classification results.

• The proposed model is more generalized and hence it can be applied to analyze thermal images acquired by different protocols/cameras used in different applications also such as skin cancer detection,peripheral vascular disease identification,night vision,surveillance,disease and pathogen detection in plants,etc.

The rest of the article is arranged in the following manner as:Section 2 describes the background theory of materials and methods.The proposed methodology including data-set and data pre-processing is provided in Section 3.Results and discussions are presented in Section 4.Section 5 and Section 6 give a brief discussion and conclude the findings,respectively.

1.1 Related Work

Owing to the limitations of currently used imaging modalities,thermal imaging is continuously being evaluated for breast cancer screening and detection.A brief literature review based on the wide range of research publications related to breast cancer detection and classification is being presented in this section.

The medical thermogram analysis is directly dependent on the quality of the thermogram which mainly depends on acquisition protocol,used thermal camera,and signal to noise ratio of thermogram [1].The current status of infrared thermal imaging techniques in breast cancer detection,classification,and a few protocols to acquire thermograms have been studied by [3,6].In general,all computer-aided automated and semi-automated thermogram-based cancer detection systems involve three basic steps,i.Pre-processing and segmentation of the region of interest(ROI):it normally includes background removal and ROI separation for further processing,ii.Texture enhancement and noise reduction in thermogram,iii.Appropriate feature extraction and classification [9-13,20-26].

Thermal images have a low-intensity gradient,absence of clear edges,and high noise to signal ratio [27].Therefore,the precise segmentation of ROI and analysis of breast cancer become inaccurate and difficult.Thus,many researchers have also reported manual segmentation of ROI and Left/Right regions for symmetrical analysis [10-15,20,21].In the case of breast cancer detection,the segmentation of ROI indicates the separation of breast tissues from the rest of the body and the background.Various semi-automatic and fully automatic ROI segmentation methods based on image processing techniques such as edge detection [15,20],region growing [21],thresholding [25,26],and morphological approaches have been delineated in literature [14,26].Since the proposed work focuses only on breast cancer detection and classification,the ground truth masks of respective ROIs of the breast thermal images which are available in the user database have been utilized to achieve the maximum analysis accuracy [28].

In order to improve detection accuracy,researchers have applied several image enhancement and de-noising techniques in spatial and transform domains.The spatial filters such as gaussian,wiener filter and median filter,etc.,blur the edges.While the transform-domain techniques like contourlet,wavelet,and curvelet with diffusion and adaptive anisotropic diffusion filtering have been widely employed to enhance and de-noise the thermal images.As thermal images have smooth transitions in intensity values,the wavelet-based de-noising also does not assist well the thermal images [27].Some other techniques such as the BM3D technique based on enhanced sparse representation have been reported which are capable of sharpening and de-noising low contrast thermograms [7].Recently,fractional derivative-based techniques have been applied to enhance the texture of various images as it preserves the weak textures while suppressing the noise in the images [29].This approach has also been explored to enhance and segment medical images [19].The tissue malignancy or tumors have abrupt textures in comparison to the normal tissues due to the process of angiogenesis.Therefore,the features having texture discrimination properties have been employed on thermal images for the segmentation of suspected regions,detection,and classification in many medical applications [30].

Consecutively,to automate the process of abnormality detection and classification in breast thermograms,different asymmetry-based analyses using machine learning techniques have been applied.A brief summary of the state-of-the-art schemes reported in the literature with user database,types of features,classifier,and the values of performance parameters accounted in the scheme are summarized in Table 1.

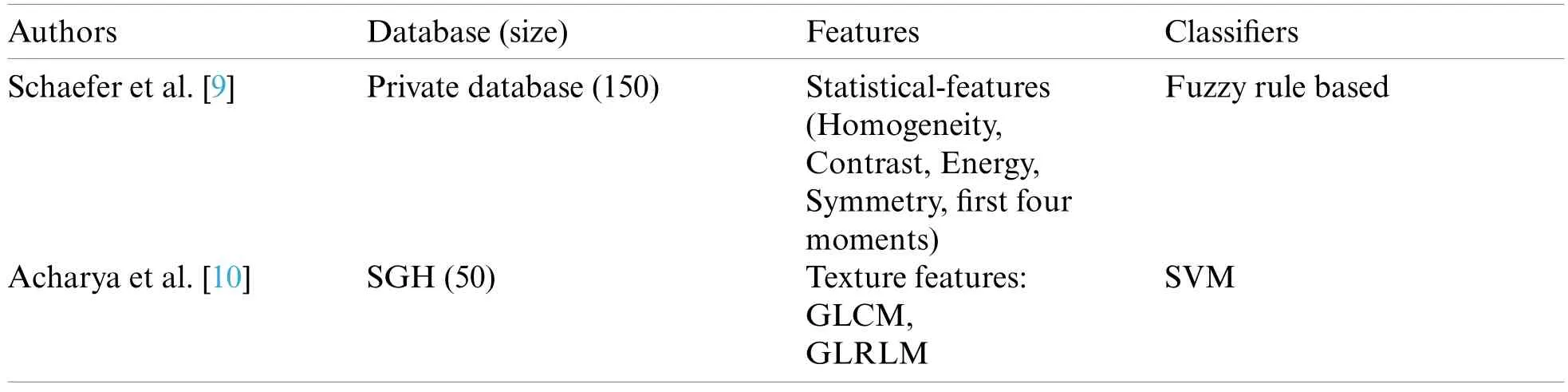
Table 1:Brief description of the state-of-the-art-techniques

(Continued)

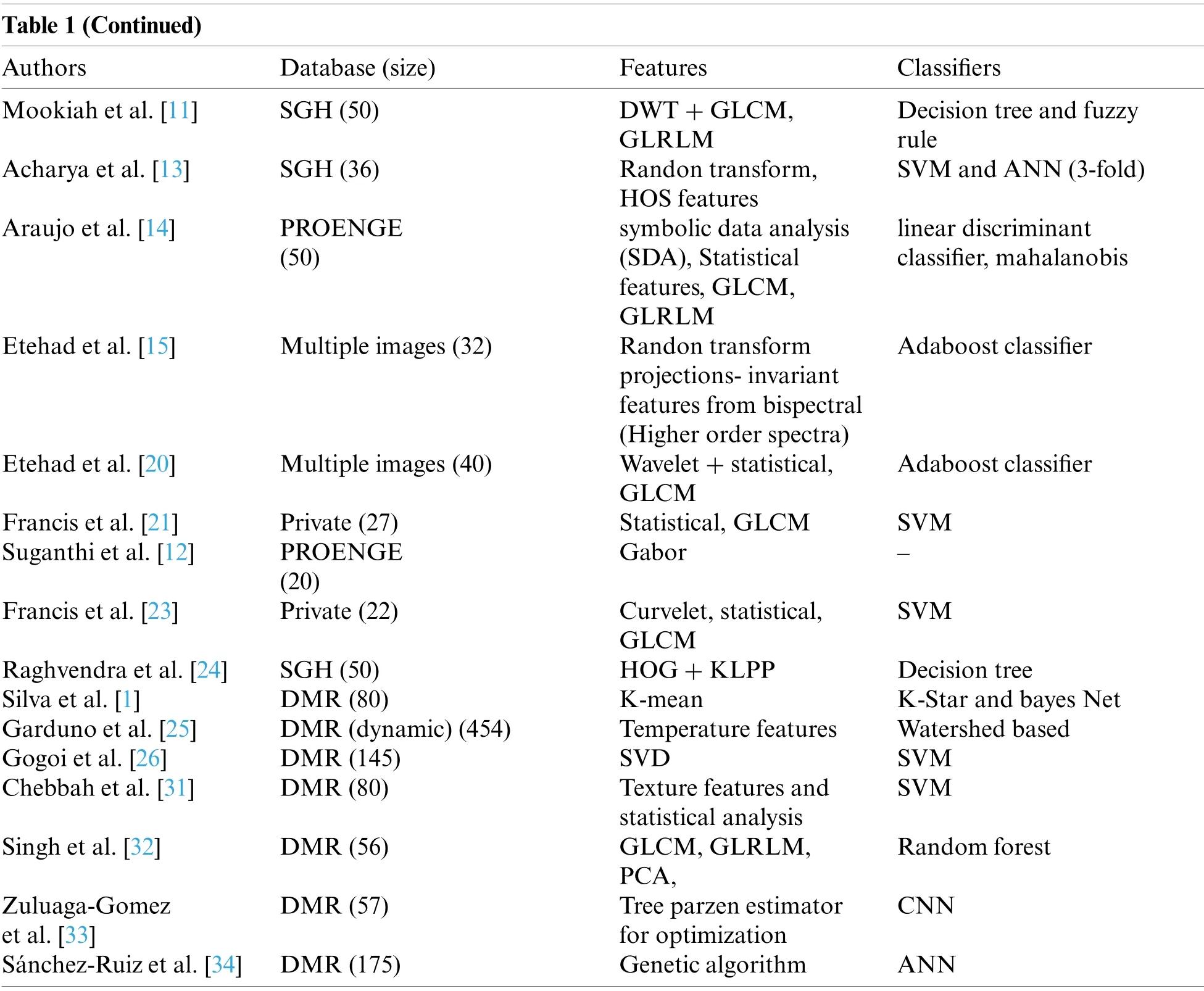
Table 1(Continued)AuthorsDatabase(size)FeaturesClassifiers Mookiah et al.[11]SGH(50)DWT+GLCM,GLRLM Decision tree and fuzzy rule Acharya et al.[13]SGH(36)Randon transform,HOS features SVM and ANN(3-fold)Araujo et al.[14]PROENGE(50)symbolic data analysis(SDA),Statistical features,GLCM,GLRLM linear discriminant classifier,mahalanobis Etehad et al.[15]Multiple images(32)Randon transform projections-invariant features from bispectral(Higher order spectra)Adaboost classifier Adaboost classifier Francis et al.[21]Private(27)Statistical,GLCMSVM Suganthi et al.[12]PROENGE(20)Etehad et al.[20]Multiple images(40)Wavelet+statistical,GLCM Gabor-Francis et al.[23]Private(22)Curvelet,statistical,GLCM SVM Raghvendra et al.[24]SGH(50)HOG+KLPPDecision tree Silva et al.[1]DMR(80)K-meanK-Star and bayes Net Garduno et al.[25]DMR(dynamic)(454)Temperature featuresWatershed based Gogoi et al.[26]DMR(145)SVDSVM Chebbah et al.[31]DMR(80)Texture features and statistical analysis SVM Singh et al.[32]DMR(56)GLCM,GLRLM,PCA,Random forest Zuluaga-Gomez et al.[33]CNN Sánchez-Ruiz et al.[34]DMR(175)Genetic algorithmANN DMR(57)Tree parzen estimator for optimization

2 Background

In this section,the back ground theory of material and methods,required for implementation of the proposed model are presented.

2.1 Fractional Differential Filter

The Gr¨umwald-Letnikov definition of the fractional differential is a basic extension of the natural derivative to fractional one and is widely being used in image processing applications [29].It is described for a functionf(x)∈[a,b] using Eq.(1):

where ≤x≤b,,n∈N,αis the order that is real number and includes fractional number.The binomial coefficient is calculated using Eq.(2):

IfI(x,y)be the image of size MXN,fractionalize imageΔαI(x,y)can be represented by using fractionalization algorithm described in Eqs.(3)-(6):

whereΔrepresents an arbitrary operator

and W ≥3 is an integer constant,,andΓis gamma function.

2.2 Texture Based Features

In this section,various textures-based features are discussed briefly.

2.2.1 First Order Statistical Features(FOS)

The first-order statistic features report gray intensity dispersion in an image.The commonly used features are mean,variance,kurtosis,skewness,energy,and entropy [8].The details of FOS features are given in Appendix A.

2.2.2 Second Order Statistical Features(SOS)

The features calculated from second-order statistics provide the relative information or position of different gray levels within the image.SOS features measure the regularity,coarseness,and smoothness of the image pixels.The widely used methods for texture discriminations are mentioned below:

(a)Gray level co-occurrence matrix features(GLCM)

GLCM describes the textural details of an image and it is useful for classifications of images.These features are found using a co-occurrence matrix where pixels are considered in pairs and the gray level co-occurrence matrix reflects the relationship amongst all pixels or groups of pixels [35].The GLCM represents a two-dimensional histogram which itself is a component of two parameters,the relative detachment between two pairs of pixels estimated in pixel numbers(d= 1,2,3...)and their relative directionθ(i.e.,θ= arctan(Δy/Δx)).Theθis the quantized orientation(00,450,900,and 1350)in four orientations,i.e.,horizontal,diagonal,vertical,and anti-diagonal respectively.Also,the normalized co-occurrence matrixCθ,dis given by the Eq.(7)as:

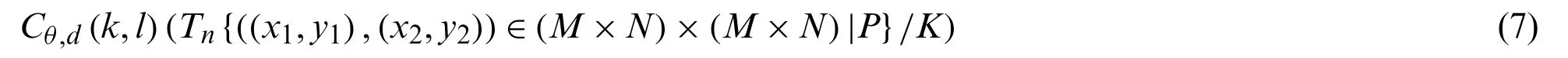
where;Pis a primary condition which satisfies the values:{Δx=dsinθ,Δy=dcosθ,I(x1,y1)=i,I(x2,y2)=j.TnandKare the number of elements in the set and the total number of pairs of pixels respectively [27].The detailed explanation with formulae of GLCM features are given in Appendix B [35].

(b)Grey level run length matrix features(GLRLM)

GLRLM is a method towards extracting second-order statistical features.The study shows that GLRLM can discriminate textures which can not be discriminated by GLCM based features extraction.This method computes the figure of gray level runs of different lengths.Where a gray level run is a set of linearly adjoining pixels of alike gray level values and the number of pixels within the run is gray level run length [36].The GLRL matrix is represented byR(θ)=[r(k,l|θ)]where each elementr(k,l|θ)specifies an approximation to the number of instances in an image and includes a run with lengthlfor intensitykin directions of angleθ.Four GLRL matrices can be calculated for(00,450,900,and 1350)[36].These GLRLM features are defined mathematically in Appendix C [36].

(c)Linear binary pattern features(LBP)

Discriminative power,computational simplicity,and rotation invariant linear binary pattern operator is a very popular approach in various applications of classification.This texture operator tags the image pixel by thresholding its neighborhood and specifies binary numbers to their neighbors as a result.It generates aP-dimensional histogram which is used as a texture descriptor [37].TheLBPP,Rnumber that characterizes the image texture around the center pixel(xc,yc)with gray level valueνcis given by Eq.(8):

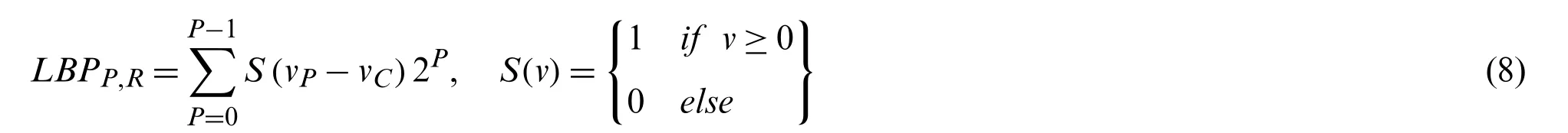
where,Pdenotes the number of equally spaced pixels (with valuevp)on a circle of radiusR(R>0)symmetrical about centre pixel.

(d)Histogram of oriented gradient features(HOG)

HOG feature descriptor outperforms significantly the other feature sets including wavelets for some applications.HOG is determined on an intense grid of equally gapped cells and also applies overlapping local contrast normalizations for better accomplishments.This is achieved by acquiring the local histogram over larger spatial regions labeled as blocks and using the outcome to normalize all of the cells in the block.The lengthLHOGof the HOG feature is based on the image size and some function parameter values as in Eq.(9)[38]:

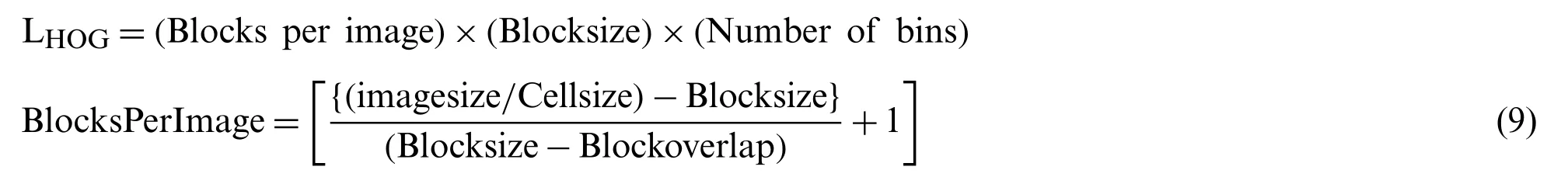
2.2.3 Gabor Wavelet Features

Gabor features are particularly suitable for texture representation and discrimination.This feature fundamentally examines if there are any explicit frequency contents in particular orientations in a local area about a point or a region.A 2D Gabor function is achieved by modulating a 2D Gaussian kernel function by a complex sinusoidal plane wave with angular frequencyωas expressed in Eq.(10),where,σx and σyare spatial spreads,andθrepresents the direction.

Thus,Gabor features are constructed by using multiple filters on several frequencies (scale)and orientationsθ[12].

3 The Proposed Model

The proposed automated breast cancer detection and classification model using fractional Sobel filter and support vector machine (SVM)with distinct texture features are described in this section.However,many schemes for breast cancer detection using thermogram with SVM reported in the literature have used either integer order filters or power-law transformation to get better signal-to-noise ratio and textural quality of thermal images [25].Moreover,comparative analysis of different texture features of thermogram commonly used with SVM or any other classifier is also missing in the literature.A new thermogram-based model for breast cancer detection using fractional derivative-based fractional Sobel filter and SVM is presented in this manuscript.Also,a comparative analysis of different texture features with fractional derivative filter is presented [39-43].

RGB color mapped thermograms obtained from the camera are first converted to gray images.This gray image conversion is essential because radiologists favor grayscale images as they comprise a greater resemblance to the mammographic images [1].These gray scale thermograms are further processed for 1:Segmentation of breast tissues from the background (pre-processing and ROI segmentation),2:Fractional Sobel filtering,3:Extraction of different features and feature reduction employing Principal component analysis (PCA),4:Training the RBF-kernel based SVM classifier using the reduced set of features and 5:Classification of breast tissues as normal or abnormal one.Steps involved in the proposed model are also depicted in Fig.1.The evaluation of the efficacy of various feature sets with the RBF-SVM classifier is also performed by calculating performance parameters.The detail of the different steps of the proposed model is described below.

3.1 Pre-Processing and Region of Interest(ROI)Segmentation

The performance of the algorithm can greatly be enhanced by accurate segmentation of ROI.In this step,the breast tissues are separated from the background region.Following are the steps used:

(1)All the input thermogramsI(i,j)are converted to grayscale images.

(2)The background subtraction is done by masking the thermal images with respective ground truth images [28].The regions other than breast tissues such as shoulders,neck,armpits,and the region below the infra-mammary are cropped out manually.

(3)The uniformity in the size of images is maintained while achieving the ROIs,i.e.,IROI(i,j).Two groups of normal and abnormal ROIs are prepared.

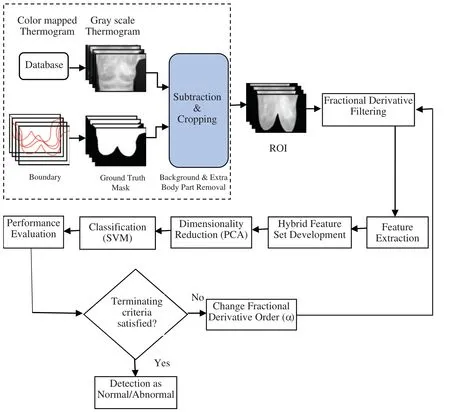
Figure 1:Schematic-diagram of the proposed thermogram adaptive breast cancer detection

3.2 Fractional Derivative Based Sobel Filtering

Fractional derivative-based Sobel filter termed as fractional Sobel filter in this paper is employed to enhance the ROI segmented thermogramsIROI(i,j).The fractional derivative based filter improves the thermal image texture quality and intensity gradient while restraining the noise enhancement [26].Thegradient components of Sobel operator can be formed to get fractional order differential forms as shown in Eqs.(11),(12)using Eqs.(5),(6):

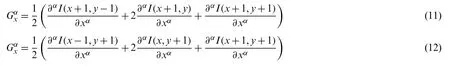
Thus,a fractional-order Sobel convolution operator forxandydirections are found by approximating Eqs.(11)and (12)and are shown in Fig.2.Where,Γ is gamma function,k=0,1,2,3...

Further,this fractional Sobel filter is applied on all thermograms.Eq.(13)depicts the masking operation on imageIROIwith fractional maskwα(p,q),whereaandbhave the valuesk/2 and 1,respectively.

Figure 2:3 × 3 Fractional-order Sobel convolution operators (a)For x and (b)For y directions

Also,Fig.3 shows the fractional derivative based Sobel masks (,)along with the values of filter coefficients in terms of fractionαandis transpose matrix of[19].

Figure 3:Fractional derivative-based Sobel mask

The Sobel fractional derivative filter masks of size 5×3 are applied to cut the computational complexity of filtering step and to enhance the discriminative power of texture features.

3.3 Feature Extraction and Dimensionality Reduction

In the proposed model,two well-founded and proficient texture feature sets are extracted from enhanced ROIs such as first-order statistical features (FOS),higher-order statistical features(HOS).Higher-order statistical features include gray level co-occurrence matrix (GLCM),gray level run length matrix (GLRLM),histogram of oriented gradient (HOG),and Histogram of a linear binary pattern (HLBP).These features imitate the association among the intensities of two image pixels or pixel sets and determine the image properties related to FOS and HOS.Gabor wavelet features capture the locality,frequency,orientation,and generate multi-resolution texture information concerning both spatial and frequency domains is also calculated.A hybrid set of statistical features is also formed by combining first and second-order statistical features,HOG,and HLBP features.The principal component analysis is done for reducing the dimensionality of the feature sets.

3.3.1 Feature Extraction

With the purpose to characterize breast thermogram and to generate a dataset for classification total of six feature extraction methods,based on effective texture are employed.First-order statistical features,second-order statistical features (GLCM,GLRLM),HOG,HLBP,Gabor wavelet,and a hybrid set of statistical features as described in Section 2 are extracted and quantified as explained below:

(1)First-order statistical features Mean,standard deviation,variance,kurtosis,skewness,entropy,and energy are extracted.

(2)Twenty-one GLCM features are extracted at distanced=1 and 2 in four orientationsθ=0°,45°,90°,and 135°,respectively.

(3)Seven GLRLM features such as SRE,LRE,GLN,RLN,RP,LGLRE,and HGLRE are also extracted in four orientations θ=0°,45°,90°,and 135°,respectively.

(4)HOG features are based on horizontal and vertical gradients.The image is divided into cells having several evenly spaced orientation bins.An unsigned gradient of 0°to 180°divided into bins is used here.A nine bins histogram corresponding to the orientation of each pixel is generated using linear-gradient voting.The contrast normalization of local responses is also performed on overlapping blocks for every cell.Each block consists of 4 non-overlapping cells of size [8×8] with 9 histogram bins.Therefore,a total of 1,764 features (36 features per block)are found.The performance of the descriptor is directly proportional to the size of histogram bins which characterizes the texture of tissue regions.

(5)HLBP features are extracted by generating a p-dimensional histogram of the image.The values ofP=8 andR=1 are taken for the purpose of this study.

(6)Gabor wavelet features are computed by convolving Gabor-wavelet filters with the image.Gabor wavelet filters are generated for five distinct scales in eight orientations respectively with a window of size of 39×39.Down-sampling is also applied to reduce the number of Gabor features.

(7)Hybrid feature set is formed by combining first and second-order statistical features,HOG features as well as HLBP features.The experimentations are performed by taking different combinations of feature sets.However,the Gabor feature captures the local texture in the frequency domain but the detection accuracy is low and dimensionality is very high,hence not included in the hybrid feature set.

Fig.4 depicts the total sets of features extracted from thermograms.Total 7 FOS features,168 GLCM features,28 GLRLM features,1764 HOG features,and 256 HLBP features make a 1967-dimensional statistical feature vector and Gabor feature vectors with the dimension of 40960 are extracted.

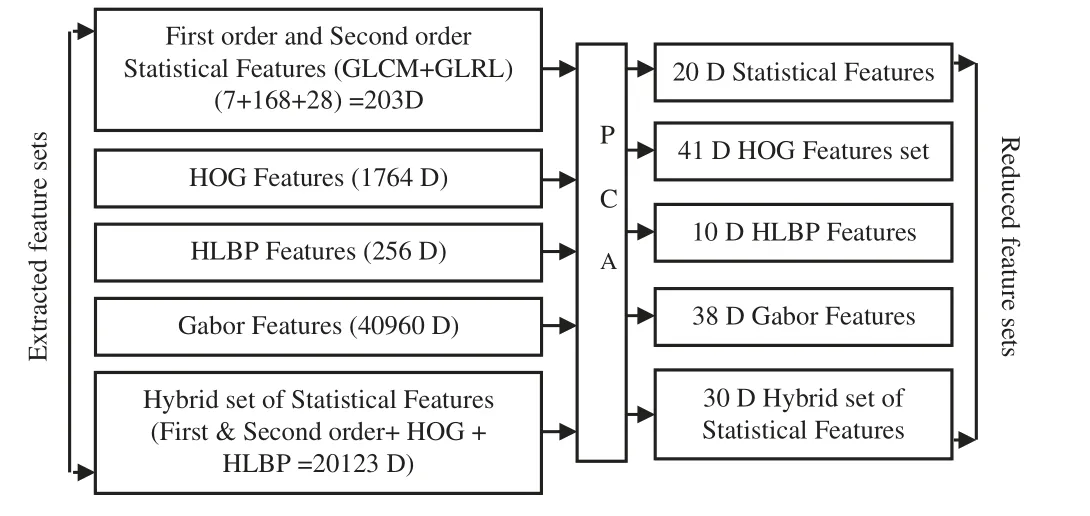
Figure 4:Extracted and reduced feature sets

3.3.2 Dimensionality Reduction of Features

The feature vectors attained from the previous step are of very high dimensions and it becomes computationally intensive to process such big data.Therefore,a linear dimension reduction technique principal component analysis is employed to slash down the dimensions of feature vector sets.Dimensionality reduction also makes the algorithms more efficient to generate more accurate predictions using machine learning algorithms.As described in [8],“PCA orthogonally transforms a set of (possibly)correlated variables in a minor set of uncorrelated variables called principal components and the number of principal components is same or less than the original variables present in dataset”.The first principal component locates the maximum variability(eigenvalue)in data and each of the succeeding components has variability in decreasing order.If PCA hasVnnon-zero eigenvectors,the optimal number of eigenvectorsVpmust be picked according to the Eq.(14)to keep the average projection error to be less than 0.01.

where,Si represents theitheigen value.The dataset must be normalized to zero mean and unit variance before applying PCA on it and 99% of the variance is kept by the feature vectors used for the next step of training and testing the classifier.Reduced sets of feature vectors for all types of texture features are also depicted in Fig.4.

3.4 Classification and Performance Evaluation

The reduced sets of feature vectors extracted from thermal images are presented as a binary classification problem and the dataset consists of feature vectors of normal and malignant classes.These vectors are further employed to train a supervised learning technique,support vector machine (SVM)with RBF kernel for classification.An SVM makes a hyper plane or a group of hyper planes in a large or infinite-dimensional space.These hyper-plane are used to distinguish the two classes as the transformed dataset develops into more distinguishable in comparison to the original input dataset [10].hyper-planes are decision boundaries that facilitate to classify the data points and the dimension of these hyperplanes is decided by the number of features.Support vectors are data points that are closer to the hyperplane and affect the orientation of the hyperplane.The data points residing on either side of the hyperplane can be characterized to different classes.

In the present work,SVM-RBF is trained with the training set of feature vectors and predictions are made for the unseen testing set.A five-fold cross-validation technique is owned to validate the model.The performance of trained classifier to identify the breast malignancy is evaluated in provisions of parameters; Specificity,Sensitivity,Accuracy and Area under the curve [15-17]:

3.4.1 Sensitivity

It is the percentage of actual positives rightly identified as positives by the classifier and is computed as:

3.4.2 Specificity

It is also known as true negative rate and is the capacity to spot the negative samples.It is computed as:

3.4.3 Accuarcy

Accuracy defines the measure of the correctness of the classifier.It can be calculated as:

3.4.4 Area under the Curve(AUC)

AUC measures the quality of the classifier.AUC is the amount of area under the receiver operating characteristics (ROC)curve which is obtained by plotting sensitivityvs.(1-specificity).Its value is between 0 and 1.The quality of diagnostic test is better if it has AUC value approaching to 1,where,TN:True negative,TP:True positive,FP:False positive and FN:False negative.

4 Results and Discussion

4.1 Experimental Set-Up and Dataset

Computer simulation outcomes of the anticipated model using MATLAB are presented in this section.Breast thermograms for this research work are taken from the database readily available under the project PROENG,captured by FLIR Thermal Cam S45.The acquisition method,protocol,and other details of the thermograms are given by [28] for further study.Sample breast thermograms taken from the selected database are depicted in Fig.5 [28],which shows the normal and abnormal thermal patterns indicating the presence or absence of suspicious regions in the breast tissues.Total of randomly selected 130 (83 normal and 47 abnormal)IR images of size 320× 240 are used for implementing the method.However,to avoid the overfitting problem,a few images have been augmented and a database of 180 (90 normal and 90 abnormal)IR images have been prepared.The number of thermal images used is also comparable with state-of-art schemes.

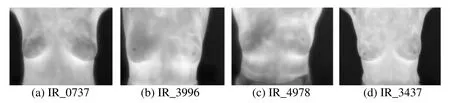
Figure 5:Sample breast thermogram images (a)Both normal (b)-(d)[28]

4.2 Results

The pre-processing,ROI segmentation,and fractional Sobel filtering with orderα= 0.2 results for four sample test thermograms used to verify the proposed model,are shown in Fig.6.In pursuance of separating the background and segmenting the breast tissues,the required ground truth masks available in the database are used [28].Fig.6a shows gray-scale normal IR_3830,IR_0737 and abnormal IR_4149,IR_8285 breast thermograms,their respective ground truth region of interest (ROI),and masks are shown in Figs.6b and 6c,respectively.Fig.6d shows the background subtracted thermograms,whereas Fig.6e depicts the background-subtracted thermograms with breast tissues only.The segmented thermograms (ROIs)are now processed through a fractional derivative-based Sobel filter as explained in Section 3.2 to enhance the images.It is noted here that the fractional-order derivative filter (FODF)considers more information of neighboring pixels,extracting more image details.Thus,it enhances the edges and preserves the weak and medium textures details simultaneously,removing the noise [27].

Figure 6:Pre-processing,ROI segmentation and fractional derivative filtering using fractional Sobel filter of order α= 0.2 steps for four sample test thermograms (1.IR_3830,2.IR_0737,3.IR_4149 and 4.IR_8285 [28])(a)Original thermograms (b)Ground truth segmentation boundaries [28] (c)Respective ground truth masks [28] (d)Background-subtracted thermograms (e)Background subtracted thermograms with breast tissues only (ROIs)(f)Fractional Sobel filtered ROI thermograms

A fractional-order Sobel mask withk=4 is used andαis varied from 0 to 1 with interval 0.1.Fig.6f shows the fractional-order derivative filtered (FODF)thermal images for the value of fractionα=0.2 in fractional Sobel filter(5×3Wxand 3×5Wy)fork=4.Experiments are performed for different values of k,but the results are better for the masks of size k=4,i.e.,5×3Wxand 3×5Wy,Hence these values are selected in the proposed model.

To study the effect of fractional derivative Sobel filter on thermal images; the quantitative analysis of gray level co-occurrence matrix (derived from the database of normal and abnormal images)which describes the comprehensive information of texture is done.A set of GLCM features (described in Section 2)is extracted in four directions 0°,45°,90°,and 135°).It is observed that the magnitude of features extracted in different directions varies in a similar manner irrespective of the direction of extraction.Thus,Tables 2 and 3 represent a few of selected features(Energy,Contrast,Entropy,Correlation,Sum of average,Sum of entropy,Information measure of Correlation 1,Information measure of Correlation 2)which are extracted in direction (0°).It can clearly be observed that the discrimination between normal and abnormal thermograms with respect to fraction α arises prominently between α=0.2 and α=0.4.

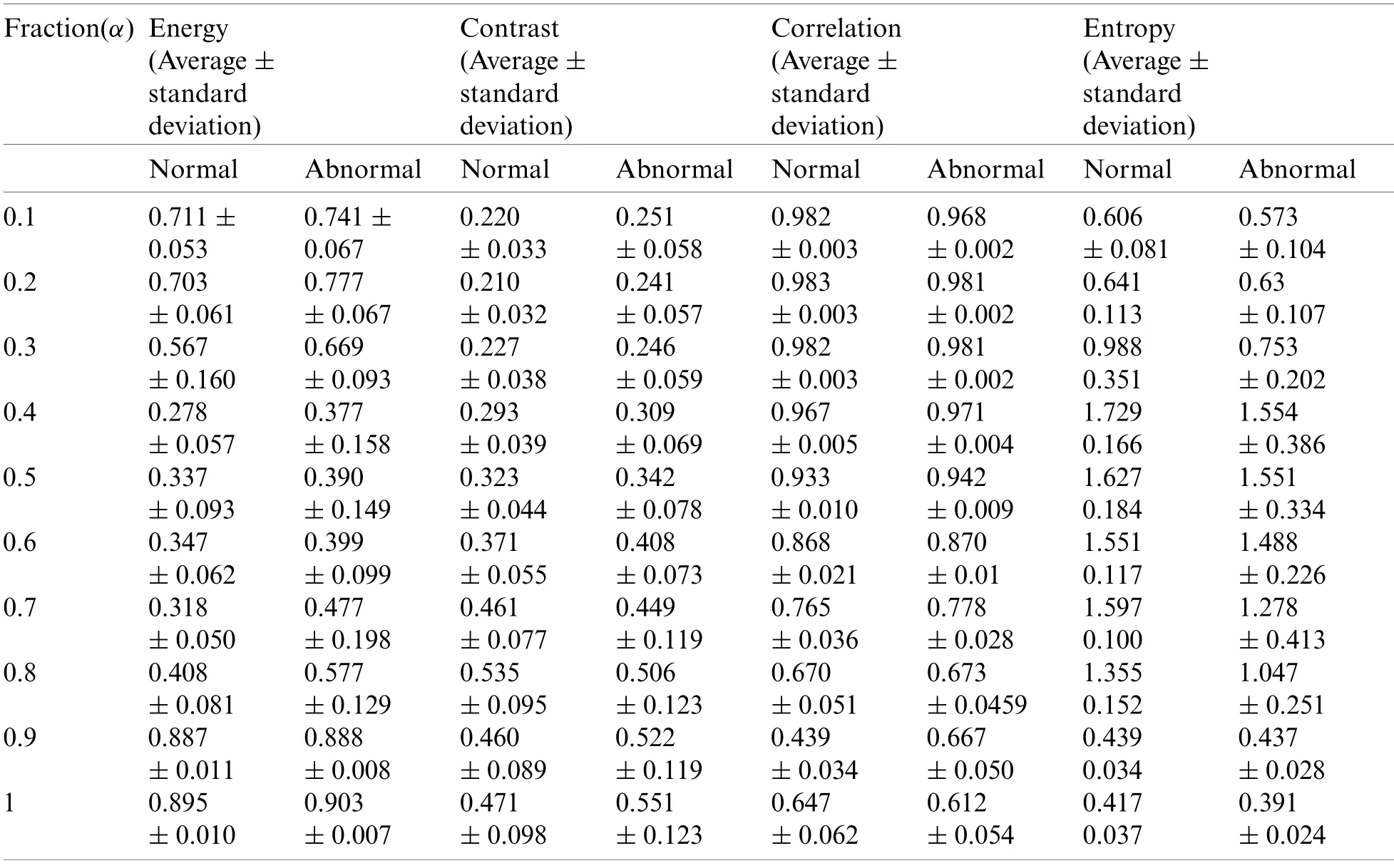
Table 2:Statistical analysis of different GLCM features with respect to derivative fractions for normal and abnormal breast thermograms

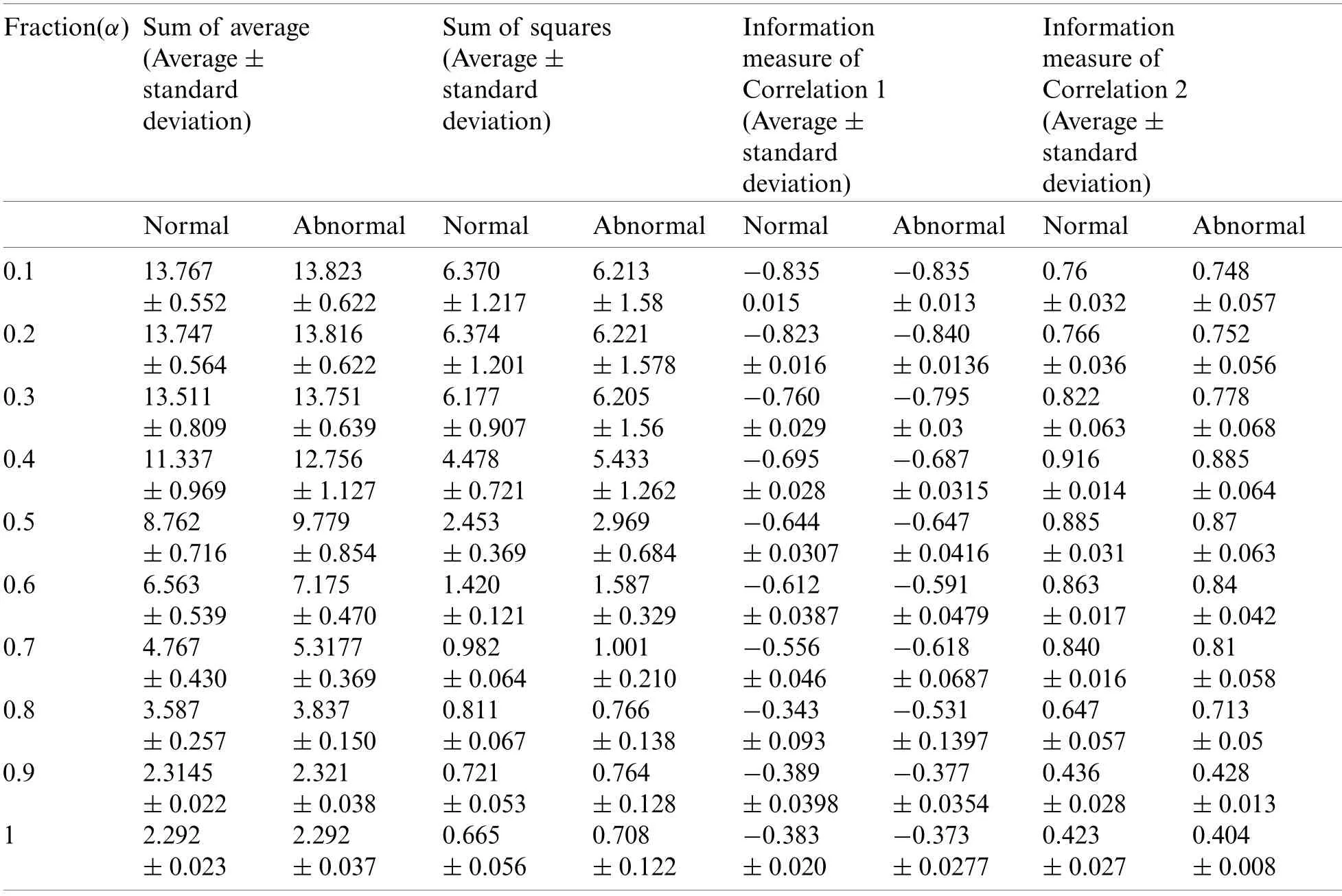
Table 3:Statistical analysis of different GLCM features with respect to derivative fractions for normal and abnormal breast thermograms

Further,the five sets of features (as mentioned in Section 3)including,first and secondorder statistical,HOG,HLBP,Gabor,and a hybrid set of statistical features are extracted from every segmented thermal image,respectively.As the dimensions of feature sets are very high,PCA is applied for dimensionality reduction.Now,these feature sets are fed to SVM-RBF for the classification of breast thermograms.It is also mentioned here that,experimentations are performed to investigate the performance of SVM with different kernel functions such as linear,RBF,etc.but the results of the RBF kernel are more improved,so the RBF kernel is used in the proposed model.

For evaluating the performance of distinct feature sets,significant classification parameters such as accuracy,specificity,and sensitivity to evaluate the trained classifier are calculated.The variation of these performance constraints for each feature set with fractional derivative parameter alfa (α)is shown in Figs.7-9.

It can clearly be observed from Figs.7-9 that the performance parameters have the most suitable values for the fraction order ofα=0.2,for all the set of features,i.e.,Gabor Features,HOGfeatures,HLBPfeatures,Statisticalfeatures,Hybrid statistical features represented as F1,F2,F3,F4,and F5,respectively.The hybrid feature (F5)has the superior performance values for the fractionsα=0.2,0.3,0.4 while the optimum values of fraction orderαfor statistical features,HOG,HLBP and Gabor features areα=0.3,0.2,0.2 and 0.3,respectively.

It is also observed from Table 4 that the results of the proposed model with hybrid features at fractionα=0.2 outperform the other feature sets with accuracy,sensitivity specificity,and area under the curve to be 94.44%,95.55%,92.22%,96.11%,respectively.Fig.10 also confirms that the HLBP feature performs comparatively better than other feature sets in all aspects of performance except that of the hybrid feature set.Further,the performance of the proposed model excels the recent state-of-the-art techniques for breast cancer detection and classification as depicted in Table 5.

Table 4:The performance parameters of the proposed model with Fractional Order Derivative Filter (FODF)at α= 0.2 with five-fold cross validation scheme (computed for each feature set)

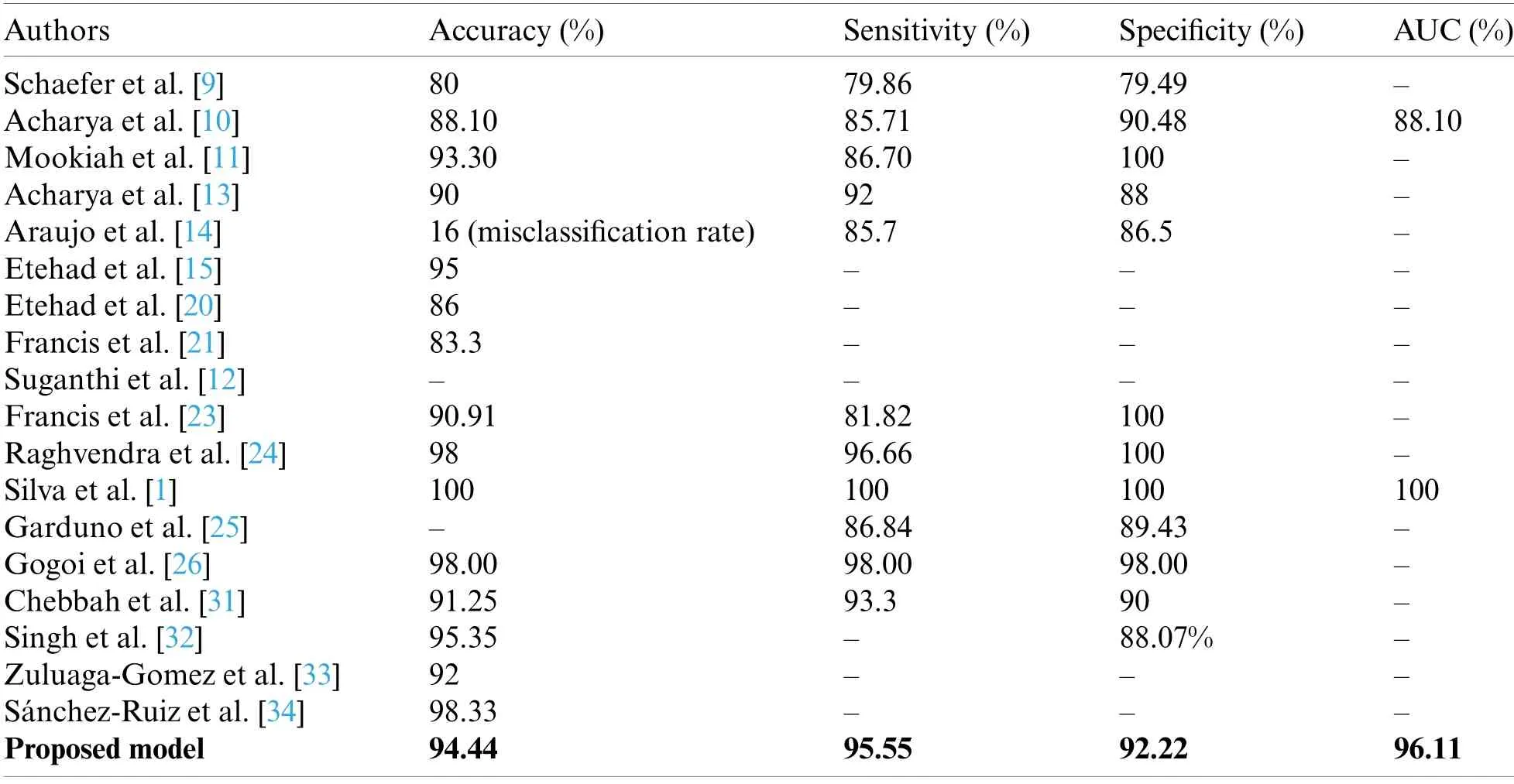
Table 5:Comparison of the proposed model with the state-of-the-art-techniques

Figure 7:Variation of performance parameter (Accuracy)with alfa

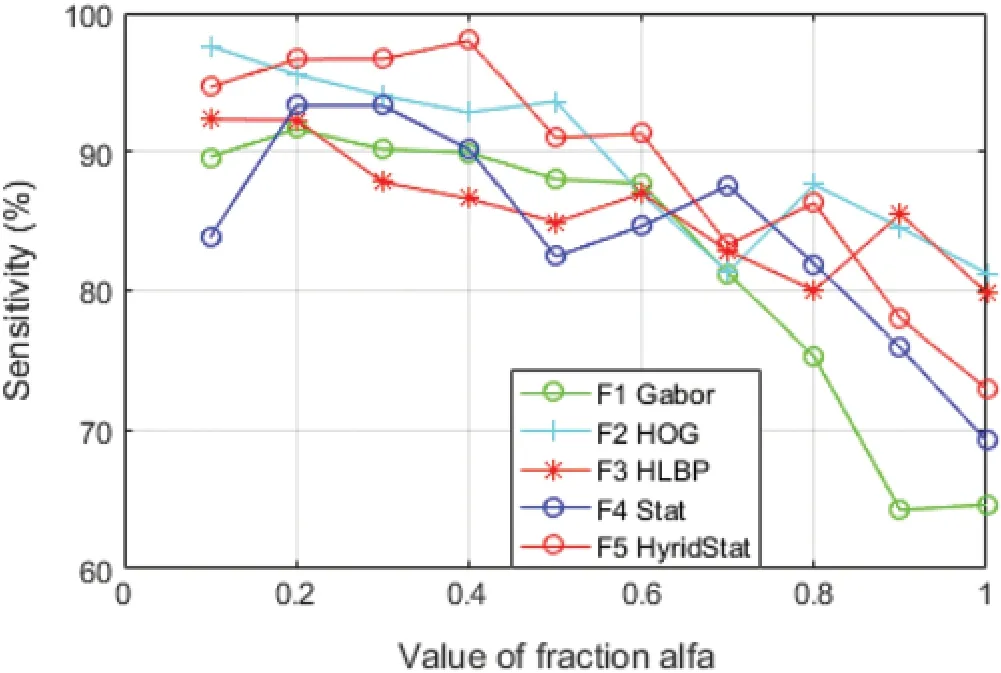
Figure 8:Variation of performance parameter (Sensitivity)with alfa

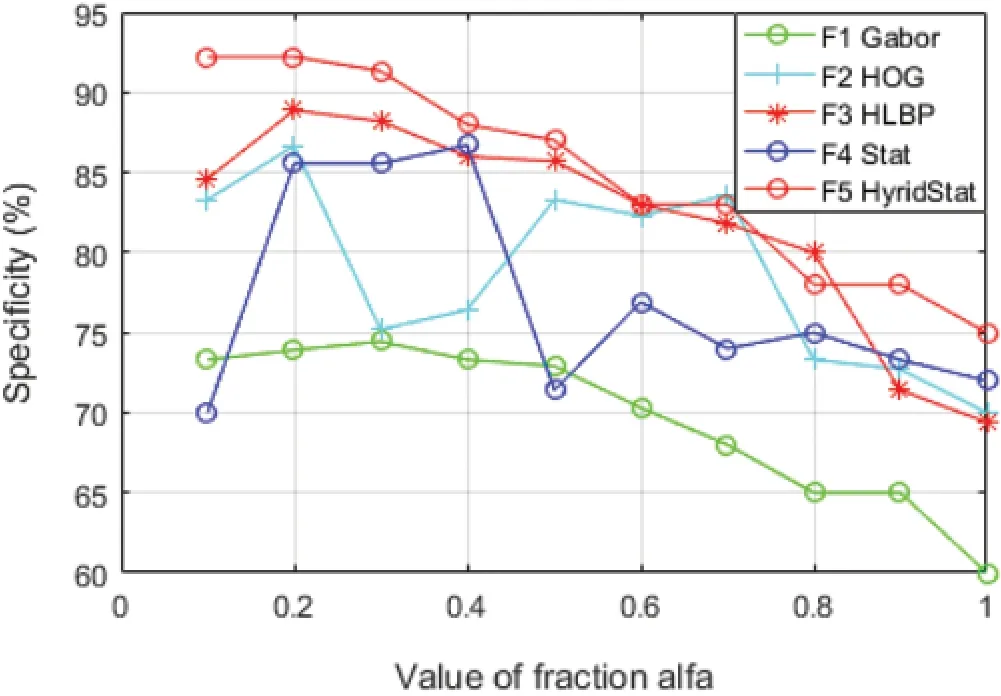
Figure 9:Variation of performance parameter (Specificity)with alfa

Figure 10:Performance parameters of proposed hybrid feature set along with other feature sets

4.3 Discussion

Asymmetry analysis-based schemes limit their performance when both breast tissues have similar abnormalities and tissue regions,because of the features measuring the abnormality result in the nonappearance of abnormality.The proposed model characterizes the thermal patterns of individual breast tissues and discovers the abnormalities.Evaluation results show that the proposed model with fractional order filtering,specific feature selection technique,classifier,explicit parameters,and the five-fold cross-validation achieves the highest performance with hybrid texture features at fraction orderα=0.2.

It is evident from the comparative analysis of the features for multiple values of alfa(Figs.7-9)that the performance of the feature set is sensitive to the value of fractionα,hence providing robustness against noise and errors by providing an additional degree of flexibility.

Comparative analysis of different features (Gabor,HOG and statistical,HLBP)presented in this paper aids the literature.HLBP features are evaluated for the first time in this paper which gives the classification accuracy of 90.55% and other performance parameters are also comparable to the state-of-art schemes.

It is worth mentioning here that the smaller size lesions and early detection problems of medical imaging modalities such as mammography,MRI,etc.could be overcome up to some extent by the proposed model.Moreover,the use of fractional order filter makes the model more generalized with an iterative selection of fractions alfa for required performance in diverse thermogram acquisition protocols and respective applications such as skin cancer,thyroid,diabetic foot,peripheral vascular disease,pathogen detection in plants,in night vision and surveillance,etc.

5 Conclusion

A new fractional-order derivative and hybrid feature set dependent thermogram adaptive computer-aided breast cancer detection model is implemented.Performance of the two new feature sets of thermogram including HLBP and hybrid feature sets are also analyzed.The hybrid texture feature set is derived by combining different texture features for improved classification accuracy.A comparative study of hybrid feature set with other popular statistical and texture features for different values of fractional orderαis also performed.For fractionα=0.2,the hybrid feature set outperforms the other feature sets and the existing techniques as well.Similarly,the HLBP texture feature set also outperforms the other feature sets except the hybrid feature set.The comparison results verify the efficacy of the proposed model,hence effectively distinguishing the normal and abnormal cases.The proposed model provides flexibility to adapt the fraction order for optimizing the classification performance against errors and degradations in the thermogram.Therefore,it is more generalized and can be used to analyze the thermal infrared images acquired by different protocols/cameras for applications other than breast cancer,such as skin cancer detection,peripheral vascular disease identification,night vision,surveillance,disease and pathogen detection in plants,etc.in an IoT environment.

Appendix A

where,M is maximum gray level value in the image.P(k)is the probability of the gray levels and is given by:P(k)=n(k)/N,where n(k)and N are total number of pixels ofgray level(k)and pixels respectively in an image.

Appendix B

where Ci,jis (i,j)thentry in the normalized GLCM and the mean and standard deviation of rows and columns are given by:

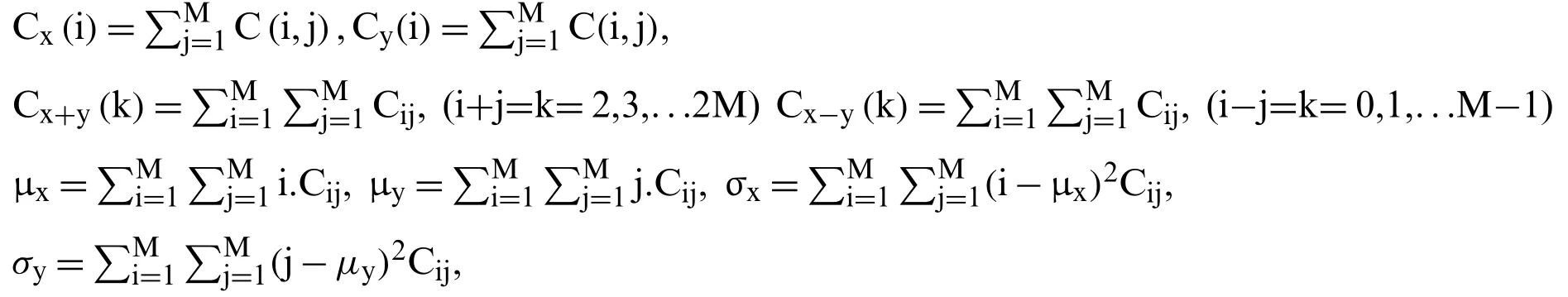
HxandHyare the entropy ofCxand Cy

Appendix C

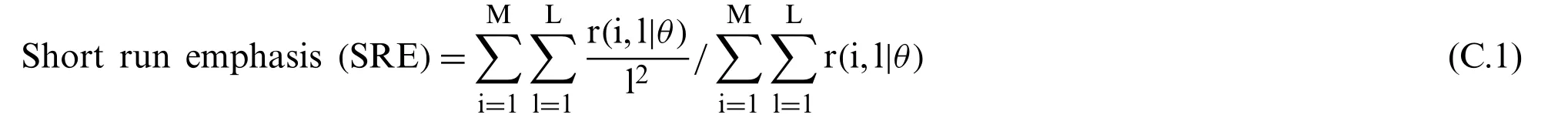
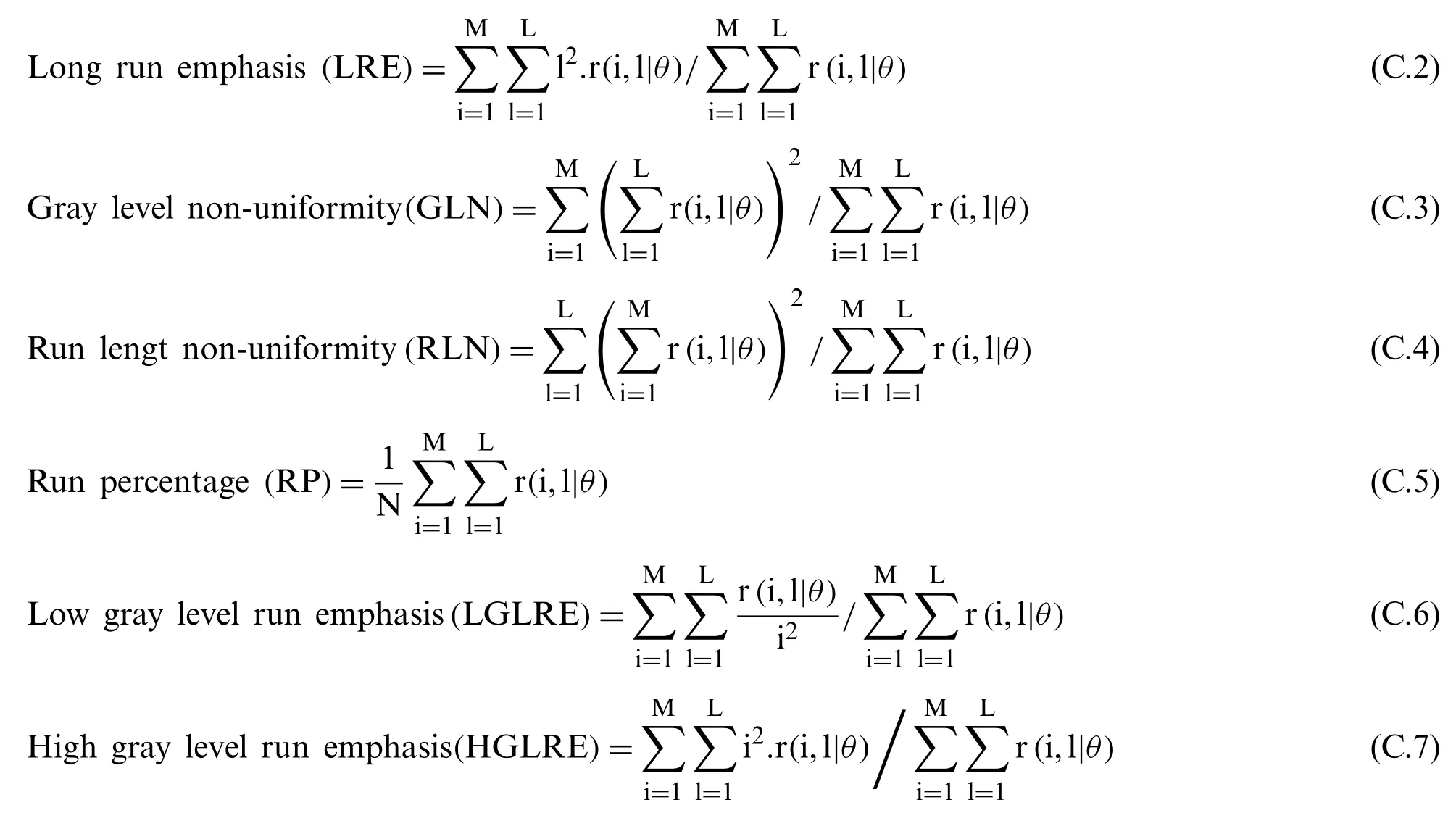
whereMandNare the total figure of gray levels and pixels in an image respectively whileLis the longest run.

Funding Statement:We would like to thank all the faculty members and technicians who provided us their scientific guidance and assistance in completing this study.Praveen Agarwal,thanks to the SERB (Project TAR/2018/000001),DST (Projects DST/INT/DAAD/P-21/2019 and INT/RUS/RFBR/308),and NBHM (DAE)(Project 02011/12/2020 NBHM (R.P)/RD II/7867).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.